考虑尾流影响的降落伞弹射拉直过程研究

王海涛 程文科



考虑尾流影响的降落伞弹射拉直过程研究

王海涛 程文科

（国防科学技术大学航天科学与工程学院，长沙410073）

降落伞的弹射拉直是其工作的第一个也是至关重要的一个环节。航天器在超声速状态下的尾流性质也非常复杂，因此，如何考虑前体航天器尾流对降落伞弹射拉直过程的影响是一个值得研究的问题。文章首先采用CFD方法计算出航天器的超声速尾流数据，然后建立降落伞弹射拉直过程的动力学模型。由于降落伞的拉直过程持续时间很短，故在研究过程中将连续尾流离散化为不同时刻的尾流，仅考虑尾流气动力对降落伞弹射拉直过程的影响。具体方法是将弹射拉直时刻计算的航天器尾流区速度场叠加于弹射分离降落伞伞包的空速上，计算考虑航天器尾流影响的伞包气动力，然后通过动力学仿真研究航天器尾流对降落伞弹射拉直过程的影响，重点研究了对伞包运动稳定性的影响。利用该方法对典型工况超声速尾流影响下的降落伞弹射分离过程进行了动力学分析，重点分析了尾流对伞包的运动轨迹和姿态的影响，研究方法和结论对稳定伞弹射拉直过程的验证评估具有重要的参考价值。

尾流影响 弹射拉直 降落伞 航天器回收

0 引言

降落伞是飞行器回收的重要气动减速装置，它利用产生的气动阻力使飞行器的全部或局部减速到规定的速度并安全着陆于地球或其他星球表面，其工作一般是整个飞行任务的最后步骤，是确保飞行器能否安全回收或减速着陆的关键，也是飞行任务成败的最终标志[1-2]。

在航天器返回过程中，一旦外部条件满足回收系统启动要求，控制装置将发出指令，通过弹射方式拉出降落伞伞包，并利用伞包和航天器之间的相对运动拉出降落伞。降落伞弹射拉直过程持续时间很短（通常1s左右），其整个过程一般位于飞行器的尾流区，具有比较复杂的力学特性。目前，针对降落伞弹射拉直过程的研究基本上都没有考虑前体尾流的影响。

国内外针对降落伞的拉直过程的研究中，LAMONT、MOOG、曹义华等[3-6]建立了一维波动方程研究了张力传播；张青斌等[7-8]建立了二维质量阻尼弹簧模型和多刚体模型研究了绳帆现象；余莉等[9]采用有限元方法建立多质点动力学模型研究了绳帆现象和牵顶伞的作用；宋旭民、王海涛等[10-12]建立了三维质量阻尼弹簧模型研究了绳帆现象、抽打现象和牵顶伞的作用。考虑飞行器尾流影响的研究中，高树义等[13-14]利用流体-刚体耦合计算的方法对考虑尾流影响的伞舱盖弹射分离过程进行了研究；WOLF等[15]研究了前体尾流对降落伞“塌陷”现象的影响；POTVIN等[16]研究了前体尾流对降落伞气动性能的影响。

本文以某型号航天器回收过程中稳定伞的弹射拉直过程为对象，研究考虑航天器尾流影响的稳定伞弹射拉直过程的动力学特性，研究方法和结论对稳定伞弹射拉直过程的验证评估具有重要的参考价值。

1 模型建立

1.1 研究方法

该型号航天器采用弹伞筒对稳定伞进行拉直开伞，稳定伞伞包安装在弹伞筒内，伞包与弹伞筒相连。弹伞筒工作后，筒盖首先分离，随后内筒和伞包组合体以一定的初始速度与航天器分离。由于弹伞筒的安装位置位于航天器的尾部，故内筒和伞包组合体的弹射拉直过程基本位于航天器的尾流区，必须对尾流的影响进行评估分析。

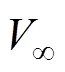
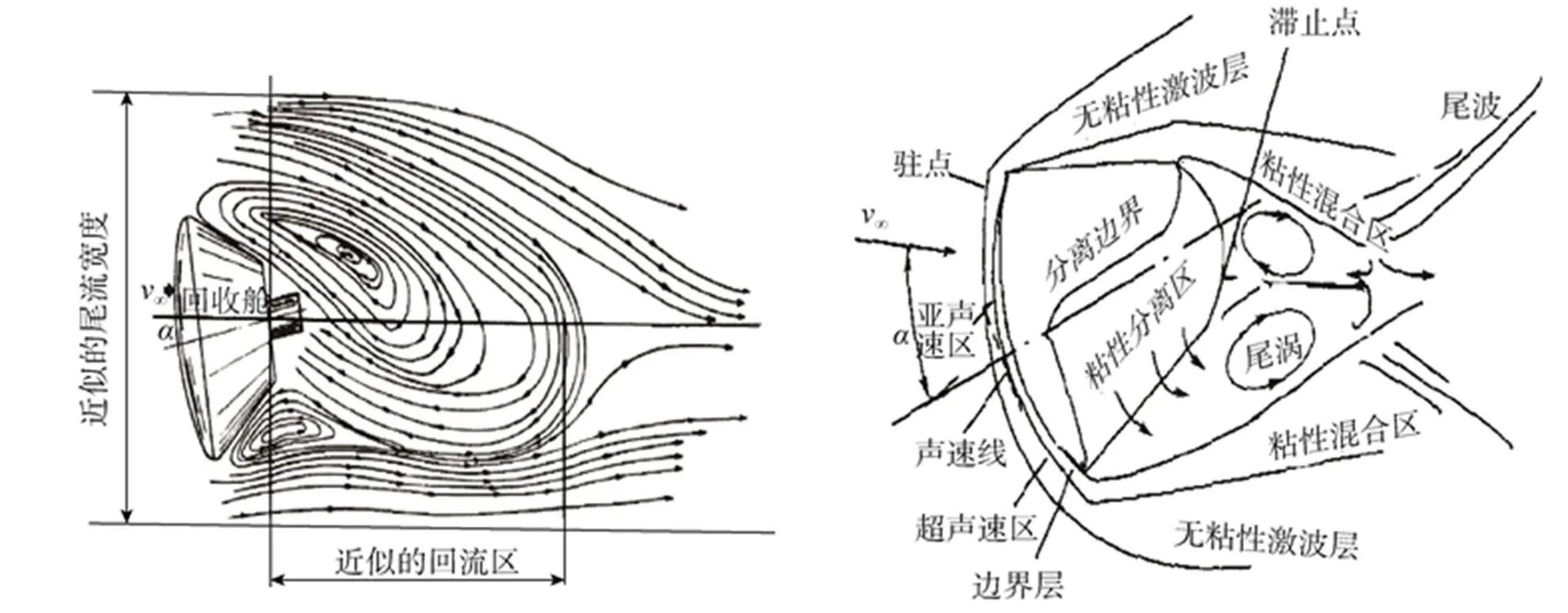
（a）亚声速尾流 （b）超声速尾流

考虑尾流影响的分离问题一般采用CFD软件的嵌套网格技术进行流体-刚体耦合计算研究，但是本文研究的稳定伞伞包在弹射拉直过程中随着伞绳和伞衣的逐渐拉出，伞包的体积和质量在不断的减小，应该建立变体积和变质量刚体模型。因此为了考虑内筒和伞包组合体在弹射拉直过程中体积和质量的不断变化，本文研究考虑将计算的航天器尾流区的速度场叠加于内筒和伞包组合体的空速上，计算考虑航天器尾流影响的内筒和伞包组合体的气动力，然后通过动力学仿真研究航天器尾流对稳定伞弹射拉直过程的影响。

考虑尾流时，设航天器大底直径为，以航天器小头面为起始截面，取10×10×12的区域为尾流数据采点区，区域以外的尾流已经比较小可以不予考虑。在区域内，根据伞包相对航天器的位置可以插值求出伞包所在位置的尾流速度，将此尾流速度矢量叠加于伞包速度上即可认为是考虑尾流影响的伞包空速，并以此空速计算伞包的气动力和气动力矩。

1.2 气动计算

设计中稳定伞伞包在超声速条件下弹射分离，因此，本文选取=3.0和=1.5两种典型工况进行研究。首先，采用CFD软件计算出航天器的尾流数据，尾流速度云图如图2所示。

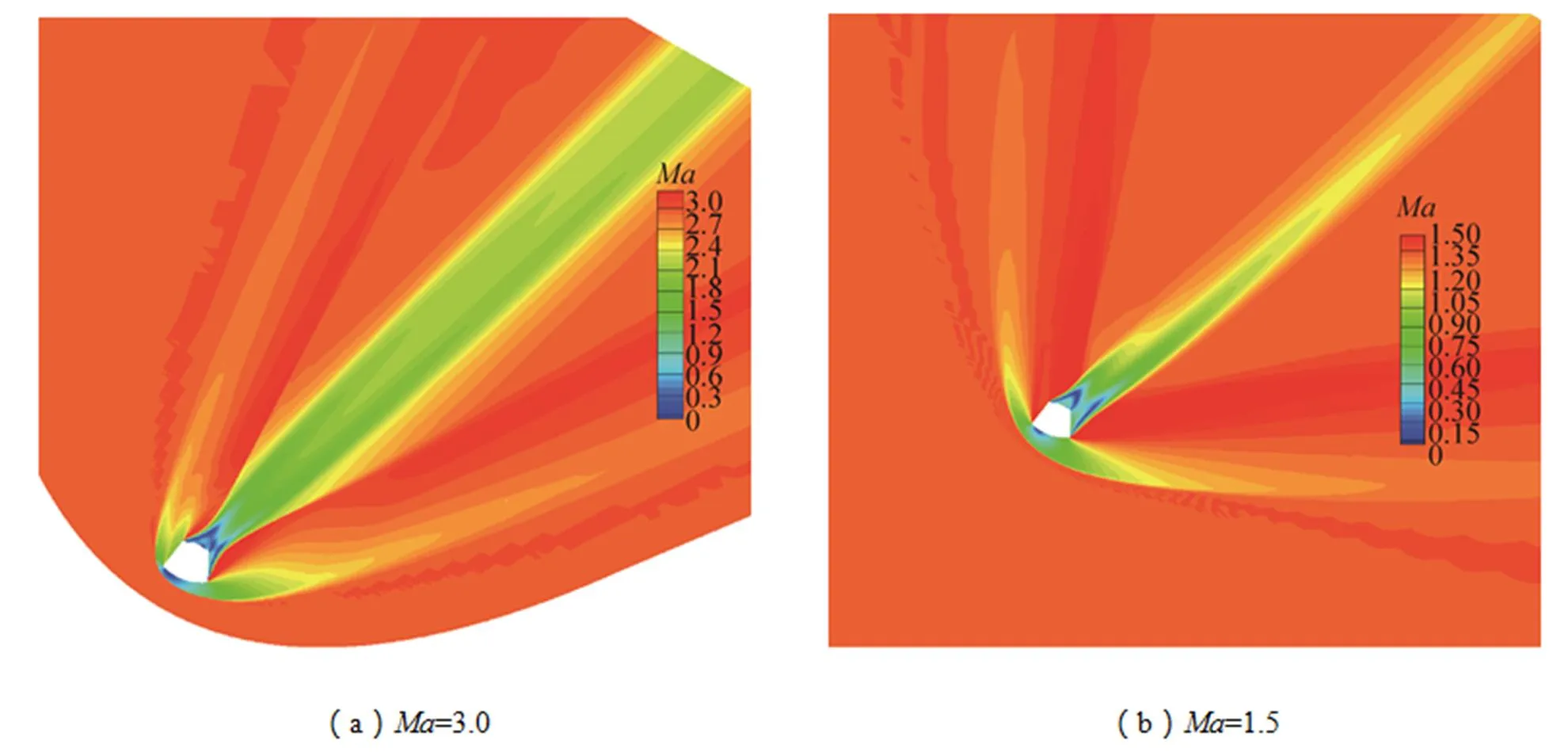
图2 航天器的尾流速度云图

由于航天器的尾流是非定常的，因此需要计算弹射起始时刻到伞包拉直结束时刻的尾流数据。稳定伞包弹射拉直时间很短（通常1s左右），故可间隔0.2s取航天器的尾流数据。若不考虑航天器尾流的非定常性，则可直接选取弹射分离起始时刻的尾流数据，将航天器的尾流视为近似定常。

在弹射拉直过程中，内筒和伞包组合体为圆柱体，其体积在不断的减小，为了计算组合体的气动力，需要利用CFD软件计算出组合体在弹射拉直初始时刻和结束时刻的气动参数，气动参数考虑、攻角、高度三个状态因素的变化。

1.3 动力学建模

降落伞的弹射拉直过程中，随着弹射内筒和伞包组合体与航天器之间的相对运动，叠放于伞包内的伞绳和伞衣逐渐拉出。在动力学建模过程中，航天器视为刚体模型，内筒和伞包组合体视为变质量刚体模型，本文仅列出伞包的动力学模型。伞包的拉直模型示意图，如图3所示。图中，伞包质量为，正在拉出部分的质量为d，受到摩擦力re和拉力的作用。

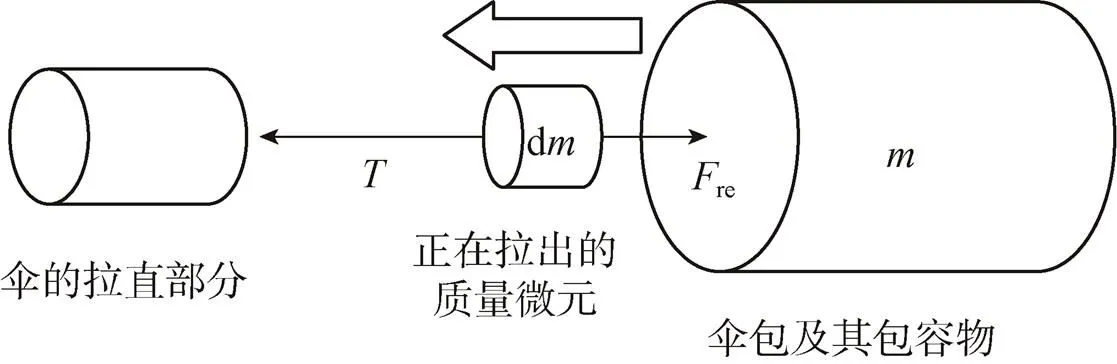
图3 稳定伞拉直模型示意

伞包所受的外力有重力、气动力和约束力，伞包所受气动力a采用式（1）计算：

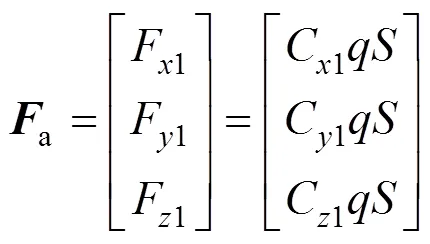
式中为动压；为伞包的特征面积；F1、F1、F1分别为伞包气动力在其体坐标系中的分量；C1、C1、C1分别为伞包的轴向力系数、侧向力系数和法向力系数。

伞包所受的气动力力矩采用下式计算：

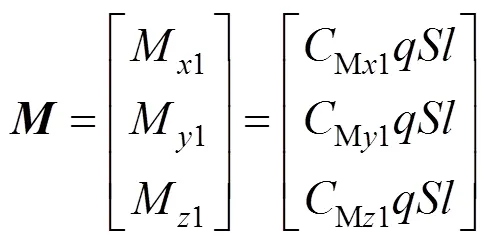
式中M1、M1、M1分别为伞包气动力矩在其体坐标系中的分量；Mx1、CMy1、Mz1分别为伞包的滚转力矩系数、偏航力矩系数和俯仰力矩系数；为伞包的特征长度。

拉直过程中伞包的高度也是随时间变化的，可由下式确定：

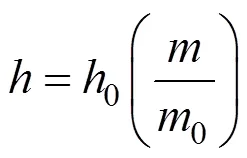
式中0和0分别为伞包的初始高度和质量；和分别为伞包的高度和质量在某一时刻的瞬时值。

拉直过程中伞包和航天器之间存在约束力，建模时认为吊带约束力的作用点在伞包下底面中心，记拉直过程中某一时刻的伞包和航天器的位置和速度矢量为1、2和1、2，则伞绳和伞衣从伞包中拉出的速度为

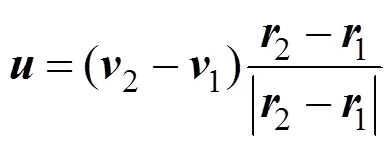
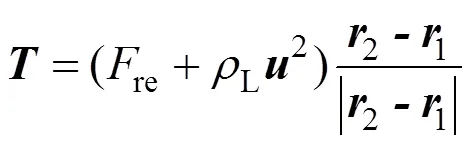
正在拉直部分的伞绳和伞衣作用在伞包上的约束力为

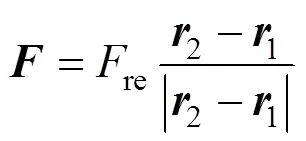
至此，即可对考虑尾流影响的稳定伞伞包的弹射拉直过程进行动力学分析。

2 仿真分析

2.1 仿真条件设置

本文针对为3.0和1.5的两种典型工况对考虑尾流影响的稳定伞弹射拉直过程进行动力学分析。工况一设置初始计算高度26 050m，初始速度1 020m/s，≈3.0；工况二设置初始计算高度21 050m，初始速度475m/s，≈1.5。为了分析不同的初始弹射速度的影响，选取25m/s、30m/s和35m/s三种初始弹射速度进行仿真分析。仿真初始时刻即为弹射分离时刻，稳定伞拉直结束时刻仿真结束。

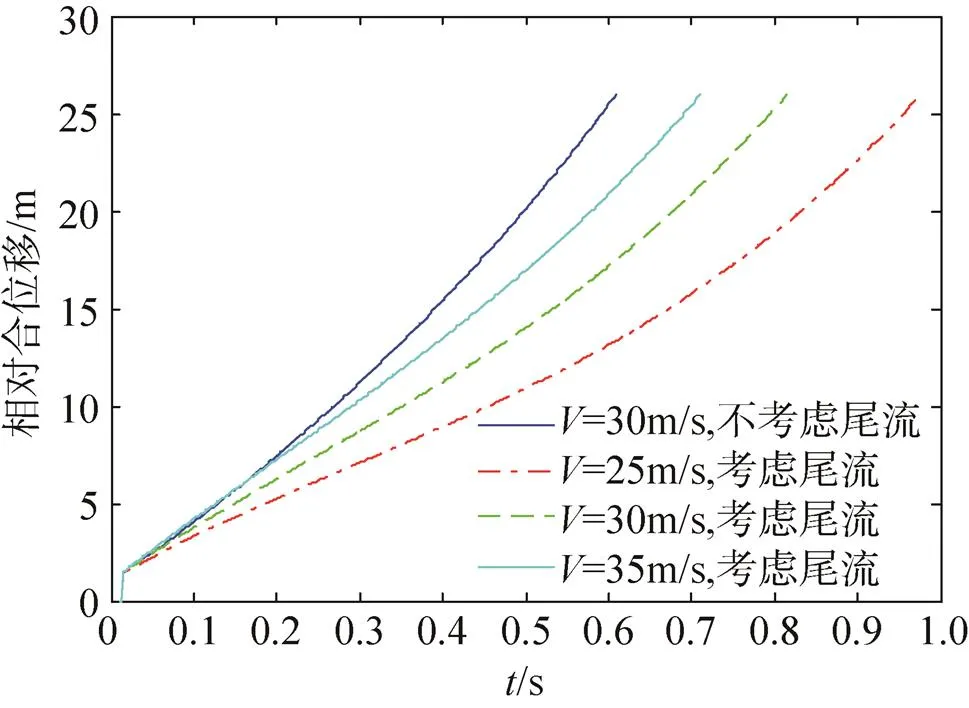
图4 工况一伞包相对航天器位移变化

2.2 典型工况分析

图4比较了工况一条件下不考虑尾流影响时伞包以30m/s的速度的弹射分离，考虑尾流影响时伞包分别以25m/s、30m/s和35m/s的速度弹射分离时相对前体航天器位移随时间的变化情况。

计算结果表明：考虑尾流影响时伞包的弹射分离过程持续时间更长，以30m/s的弹射速度为例，不考虑尾流影响时约0.6s即完成稳定伞的弹射拉直，而考虑尾流影响时则需要约0.8s才能完成，反映了尾流对稳定伞包的弹射拉直时间存在明显的影响。考虑尾流影响时，以25m/s、30m/s和35m/s的初始弹射速度分离时，从初始弹射分离到稳定伞拉直结束的持续时间为0.97s、0.82s和0.72s，反映初始弹射分离速度越大，整个稳定伞弹射拉直的过程持续时间就越短。

图5是工况一条件下整个弹射分离过程中刚体伞包的姿态随时间的变化，计算结果表明：刚体伞包在弹射分离过程中存在围绕一定平衡位置的姿态摆动。考虑尾流影响时摆动的幅度比不考虑尾流影响时要小。

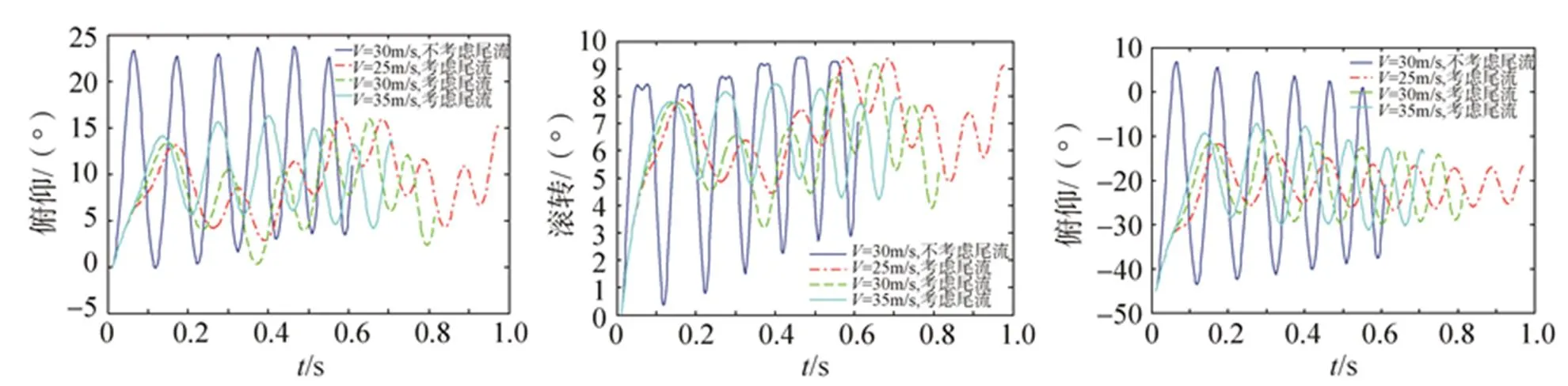
（a）偏航角随时间变化 （b）滚转角随时间变化 （c）俯仰角随时间变化

图6是工况二条件下以不同初始速度弹射分离时稳定伞伞包相对前体航天器的位移岁时间的变化情况。本计算条件下，不考虑尾流影响时以30m/s的初始速度弹射分离时，约0.7s完成稳定伞的弹射拉直，考虑尾流影响时则需要约0.9s才能完成。考虑尾流影响时，以25m/s、30m/s和35m/s的初始弹射速度分离时，从初始弹射分离到稳定伞拉直结束的持续时间为1.05s、0.90s和0.82s。

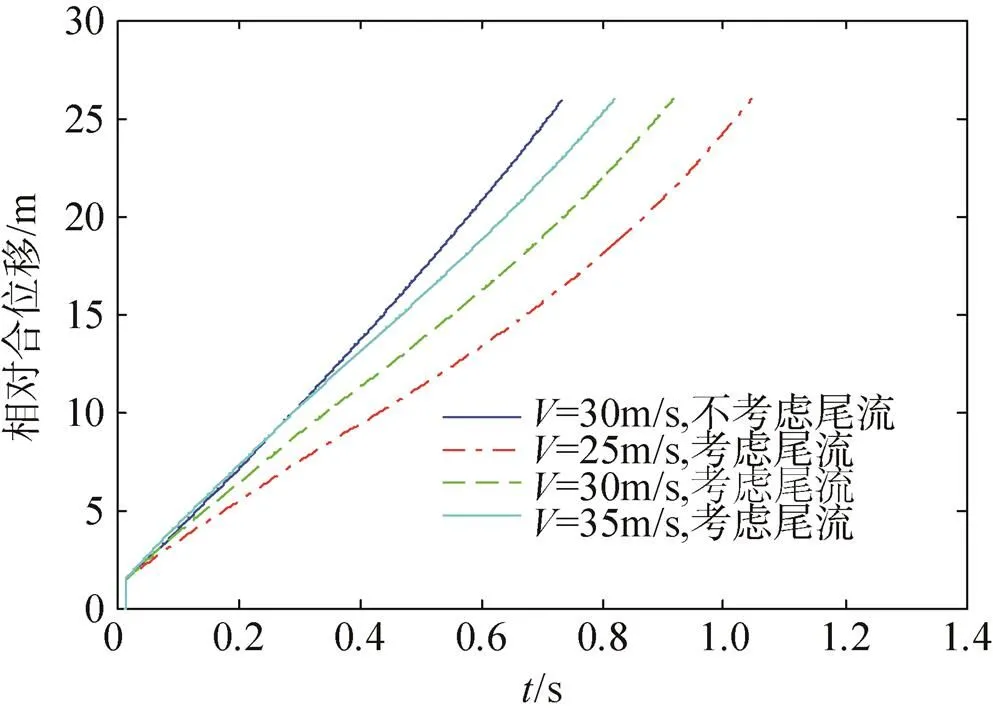
图6 工况二伞包相对航天器位移变化

图7是工况二条件下整个弹射分离过程中刚体伞包的姿态随时间的变化，仿真结果表明刚体伞包在弹射分离过程中存在围绕一定平衡位置的姿态摆动。但是与工况一不同的是，工况二下考虑尾流影响时摆动的幅度比不考虑尾流影响时要大。

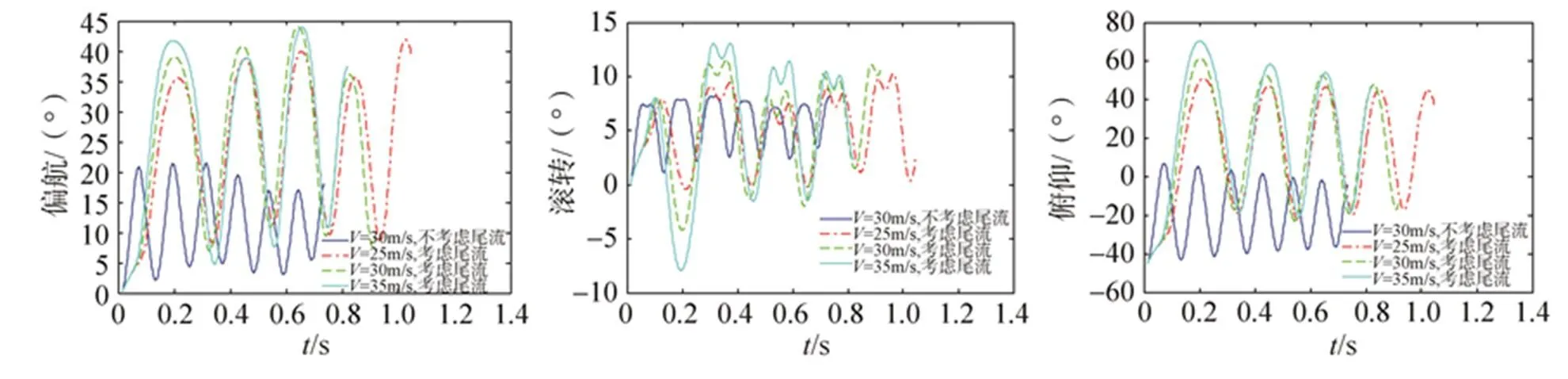
（a）偏航角随时间变化 （b）滚转角随时间变化 （c）俯仰角随时间变化

3 结论

本文针对考虑尾流影响的降落伞弹射拉直过程进行动力学研究，通过建模和典型工况的仿真分析，得出的主要结论如下：

1）不考虑尾流影响时伞包的弹射分离过程要快于考虑尾流的情况，考虑尾流时，弹射分离速度越大，弹射分离过程越快；

2）无论是否考虑尾流影响，刚体伞包在弹射分离过程中都是围绕一定的平衡位置摆动，尾流对伞包摆动幅度的影响和具体的流场分布有关。

由于航天器的尾流尤其是超声速尾流比较复杂，研究难度较大，故本文结合尾流的CFD计算结果对降落伞的弹射拉直过程进行动力学仿真研究是一种尝试，研究方法和结论可应用于降落伞弹射拉直过程的设计和验证评估。

[1] 王利荣. 降落伞理论与应用[M]. 北京: 宇航出版社, 1997.WANG Lirong. Theory and Application of Parachute[M]. Beijing: China Astronautics Publishing House, 1997. (in Chinese)

[2] EWING E G, BIXBY H W, KNACKE T W. 回收系统设计指南[M]. 吴天爵, 马宏伟, 译. 北京: 航空工业出版社, 1988. EWING E G, BIXBY H W, KNACKE T W. Design Manual of Recovery System[M]. Translated by: WU Tianjue, MA Hongwei. Beijing:Aviation Industry Publishing Company, 1988. (in Chinese)

[3] LAMONT R P. Numerical Solution of Equations Govering Longitudinal Suspension-Line Wave Motion During the Parachute Unfurling Process[D]. North Carolina State University, 1970.

[4] LAMONT R P, EARLE K H. Evaluation of Massless-Spring Modeling of Suspension-Line Elasticity During the Parachute Unfurling Process[R]. 1972. NASA TN D-6671.

[5] MOOG R D. Aerodynamic Line Bowing During Parachute Deployment[R]. 1975. AIAA 75-1381.

[6] 徐宏, 曹义华, 李栋. 先拉伞绳法数学模型及拉直利预测[J]. 航空动力学报, 2008, 23(4): 706-711. XU Hong, CAO Yihua, LI Dong.Mathematical Model and Snatch Force Prediction for the Lines-first Parachute Deployment[J].Journal of Aerospace Power, 2008, 23(4): 706-711.(in Chinese)

[7] 张青斌, 程文科, 彭勇. 降落伞拉直过程的多刚体模型[J]. 中国空间科学技术, 2003, 23(2): 45-50. ZHANG Qingbin, CHENG Wenke, PENG Yong. A Multi Rigid-body Model of Parachute Deployment[J]. Chinese Space Science and Technology, 2003, 23(2): 45-50.(in Chinese)

[8] 张青斌, 彭勇, 程文科. 降落伞拉直过程中的阻尼弹簧模型[J]. 弹道学报, 2003, 15(1): 31-36. ZHANG Qingbin, PENG Yong, CHENG Wenke. A Mass Spring-Damper Model of Parachute Deployment[J]. Journal of Ballistics, 2003, 15(1): 31-36. (in Chinese)

[9] 余莉, 史献林, 袁文明. 牵顶伞在降落伞拉直过程中的作用[J]. 南京航空航天大学学报, 2009, 41(2): 198-201. YU Li, SHI Xianlin, YUAN Wenming. Effects of Parachute Deployment Using Attached Apex Drogue[J]. Journal of Nanjing University of Aeronautics& Astronautics, 2009, 41(2): 198-201. (in Chinese)

[10] 宋旭民, 范丽, 秦子增. 大型降落伞开伞过程中的“抽鞭”现象[J]. 航天返回与遥感, 2009, 30(3): 16-21 SONG Xumin, FAN Li, QIN Zizeng. “Vent Whip” During Large Parachute Deployment[J]. Spacecraft Recovery and Remote Sensing, 2009, 30(3): 16-21. (in Chinese)

[11] 王海涛, 秦子增, 宋旭民. 大型降落伞拉直过程的抽打现象分析[J]. 国防科技大学学报, 2010, 32(5): 34-39. WANG Haitao, QIN Zizeng, SONG Xumin. Analysis of Phenomenon of Bull Whipping in the Deployment Process of Large Parachute[J].Journal of National University of Defense Technology, 2010, 32(5): 34-39. (in Chinese)

[12] 王海涛, 秦子增, 宋旭民. 牵顶伞对大型降落伞拉直过程的影响分析[J]. 国防科技大学学报, 2010, 32(4): 49-55. WANG Haitao, QIN Zizeng, SONG Xumin. Effects of the Attached Apex Drogue on Phenomenon of Bull Whipping in the Deployment Process of Large Parachute[J]. Journal of National University of Defense Technology,2010, 32(4): 49-55.(in Chinese)

[13] 高树义, 王海涛, 程文科. 月球取样返回器舱-盖分离安全性分析[J]. 宇航学报, 2014, 35(5): 499-505. GAO Shuyi, WANG Haitao, CHENG Wenke. The Capsule and Cover Ejection Separation Safety Analysis for Lunar Sample Return[J]. Journal of Astronautics, 2014, 35(5):499-505.(in Chinese)

[14] GAO Shuyi, WANG Haitao, CHENG Wenke. The Parachute Container Cover Ejection Separation Characteristic Analysis of Return Capsule for Lunar Exploration[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2014, 31(5): 552-558.

[15] SPAHR H, WOLF D F. Theoretical Analysis of Wake-Induced Parachute Collapse[C]//AIAA 7th Aerodynamic Decelerator and Balloon Technology Conference, San Diego, California, 1981: 21-23.

[16] MARK Mcquiling, JEAN Potvin. Forebody Wake Effects on the Aerodynamics of an Annular Parachute[C]//42nd AIAA Fluid Dynamics Conference and Exhibit, New Orleans, Louisiana, 2012: 25-28.

[17] 王希季. 航天器进入与返回技术[M]. 北京: 宇航工业出版社, 1991.WANG Xiji. Entry and Returning Technology of Spacecraft[M].Beijing: Astronautics Publishing House, 1991.(in Chinese)

[18] 张鲁民. 载人飞船返回舱空气动力学[M]. 北京: 国防工业出版社, 2002. ZHANG Lumin. Reentry Capsule Aerodynamics[M]. Beijing: National Defense Industry Press, 2002.(in Chinese)

（编辑：刘颖）

Research on Ejecting and Deploying Process of Parachute Considering Wake Flow Effects

WANG Haitao CHENG Wenke

（College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China）

The ejecting and deploying process is the first and important phase of a parachute, and the wake flow of the spacecraft in supersonic speed is also complicated, So how to consider wake effects of spacecraft is a problem worth researching. This paper computes supersonic wake data of spacecraft using CFD methods firstly, then builds a dynamic model of ejecting and deploying process of a parachute. The continuous wake can be discreted by times because the deploying process lasts short, and just the aerodynamic force effect on the wake flow is considered. The detailed method is as follows, when calculating the aerodynamic force of parachute bag, take the wake velocity of spacecraft additive to the velocity of parachute bag, then analyze the dynamic character of ejecting and deploying process through numerical simulation, especially the motion stability of the parachute bag. This paper researches on ejecting and deploying process of parachute considering supersonic wake of spacecraft under typical conditions, especially analyzes the trajectory of motion and attitude of the parachute bag. The analysis method and conclusion can provide important reference value for validation and evaluation of ejecting and deploying process of parachute.

wake flow effects; ejecting and deploying; parachute; spacecraft recovery

V448.15

A

1009-8518(2017)05-0003-07

10.3969/j.issn.1009-8518.2017.05.001

王海涛，男，1982年生，2011年获国防科学技术大学航空宇航科学与技术专业博士学位，讲师。研究方向为航天回收着陆技术。E-mail: htw2000@163.com。

2016-04-19

国家重大科技专项工程