遥感卫星图像几何定位精度评估方法浅析
2017-11-25田国梁黄巧林何红艳夏中秋
田国梁 黄巧林 何红艳 夏中秋
遥感卫星图像几何定位精度评估方法浅析
田国梁 黄巧林 何红艳 夏中秋
(北京空间机电研究所,北京 100094)
遥感卫星图像的几何定位精度是卫星遥感能力地面预估或在轨评价的重要指标之一。利用传统评价方法得到的几何定位精度不能完全反映遥感卫星的定位能力,针对不同的几何定位精度,需要更加准确的评价方法。文章首先介绍了几何定位精度的概念,并且分析了内部和外部几何定位精度的区别;其次通过对中误差和圆概率误差的研究,比较其各自的优缺点;最后采用不同的几何定位精度评价方法对仿真数据进行评估,结果表明选择合适的几何定位精度评价方法可以得到更准确可靠的评价结果。
几何定位精度 中误差 圆概率误差 评价方法 航天遥感
0 引言
近年来我国多颗高分辨率光学遥感卫星的成功发射与在轨运行,在对地目标观测领域有了长足的发展[1-2]。光学遥感卫星在轨数量的增多,不仅使我国具备了快速获取全球区域内高分辨率光学影像的能力,而且卫星遥感图像的分辨率及辐射质量也大幅提高[3-4]。随着航天遥感“看不清”问题的初步解决,卫星定位“测不准”的问题则日益凸显[5-6]。遥感卫星几何定位精度这一指标就是评价卫星是否“测得准”的重要依据。因此选用正确合适的几何定位精度评价方法是十分重要的。
研究人员围绕如何“测得准”这个问题做了大量研究[7-9],其中最为基础的是卫星几何定位精度的评价方法的研究。文献[10]在有控制点的条件下,利用传统中误差评价方法对中巴地球资源卫星01星(CBERS-01)遥感图像做了几何定位精度评价;文献[11]采用EFP多功能光束法平差对“天绘一号”03星的卫星遥感影像进行处理,最后利用传统中误差评价方法,在无地面控制点的条件下对其几何定位精度进行了评估;文献[12]探讨了基于有理函数模型的GeoEye-1立体定位方法,并采用圆概率评价方法对澳大利亚Hobart地区立体像进行了几何定位精度的评价;文献[13]提出了基于SIFT特征的自动几何精校正方法,并采用圆概率误差和中误差两种评价方法对航空高光谱成像仪Hymap获取的新疆东天山数据进行定位精度评价。因此,合适的几何定位精度评价方法不仅能提高评价的可靠性,同时也能解决各个卫星在几何定位精度上无法比较的问题。
本文从遥感卫星几何定位精度的概念出发,通过分析不同需求背景下的几何定位精度和传统的中误差评价方法与圆概率误差之间的区别和联系,给出了适合不同条件下卫星几何定位精度评价的计算方法,并且通过仿真计算进行了验证。
1 遥感卫星几何定位精度
遥感卫星的几何定位精度是指通过遥感图像获取目标点的地理位置与目标点实际地理位置之间的偏差,其计算就是通过统计学的方法对遥感图像上的点与实际地面位置之间的误差(即几何定位误差)进行处理,得到代表整幅图像及卫星几何定位的评价精度[14]。
根据误差的来源,几何定位误差可以分为随机误差和系统误差,其中随机误差一般服从正态分布,而系统误差与测量设备、条件、目标等因素有关[15-16]。
根据计算的样本不同,几何定位精度分为垂轨、沿轨、平面和高程等几种。其中垂轨、沿轨和高程是单一方向上的几何定位精度,平面几何定位精度是二维的几何定位精度[17-18]。
根据评价的内容不同,几何定位精度又分为内部几何精度和外部几何精度。内部几何精度是指针对图像内部几何变形,如长度变形、角度变形和仿射变形等,对其变形的绝对量和整幅图像变形的一致性的评价,又叫相对定位精度[19]。因此内部几何精度是针对卫星遥感定位算法的评价,是测量算法中参数理论精度的表现形式,与测量的算法有关。外部几何精度是指经过几何校正后的遥感图像产品上选定的多个参考目标的坐标位置与其实际位置之间的偏差,也就是校正后的像点对应的地理位置和真实地理位置之间的差异,也称绝对定位精度[20]。所以外部几何精度与目标测量定位方法无关,只与校正后的目标像点位置与实际位置之间的误差有关。
由以上概念可知,内部几何精度是对系统误差进行处理的结果;当进行理想几何校正后,即系统误差完全被校正消除,外部几何精度是对随机误差进行处理的结果[21]。但在实际卫星工程中,系统误差和随机误差无法精确剥离,系统误差也不能完全校正,因此在对卫星遥感几何定位精度评价时,应该注意采用合适的评价方法。
2 几何定位精度评价方法
卫星遥感图像几何定位精度的评价方法一般有两种:一种是基于中误差的传统评价方法,另一种是基于圆概率误差的评价方法。
2.1 传统中误差评价方法
在2002年制定的国标——《航天遥感图像定位精度检测方法》中,规定了航天遥感图像的几何定位精度评价方法。评价方法首先通过遥感图像的目标点获取其对应在地面的位置作为被测点坐标,然后通过外业测量方法、地形图库读点法或者摄影测量方法得到同名检测点的实际地理坐标,最后计算被测点与实际点坐标值之间的误差,统计其中误差。得出的中误差即为航天遥感几何定位精度。
设X=x-x0;Y=y-y0
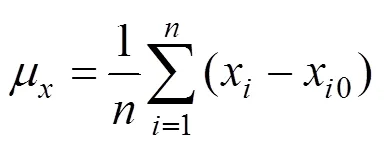


式中 (x,y)为被检测点通过图像获取的地理坐标;(x0,y0)为同名检测点实际的地理坐标;X,Y为实际坐标与获取坐标之间在沿轨和垂轨方向的几何定位误差;σ为沿轨方向的几何定位精度;σ为垂轨方向的几何定位精度;σ为平面几何定位精度;μ,μ为定位误差的均值;为检测点个数。当样本定位误差X,Y中不含系统误差,只含有随机误差时,均值μ,μ为零,因此均值μ,μ反映了定位误差中的系统误差分量。
由式(1)、(2)可知,传统中误差评价方法的核心在于中误差的计算,得出的几何定位精度σ,σ,即求其样本数据的标准差,其物理意义为样本中被检测点的定位误差落在[–,+]中的概率为68.26%(2的置信概率为95.44%,3的置信概率为99.74%)。在计算单一方向上的几何定位精度σ,σ时,其置信概率满足68.26%,但当计算平面定位精度σ时,置信概率小于68.26%。因此,在计算单一方向上的几何定位精度(沿轨、垂轨),传统的中误差评价方法比较简单可靠。
2.2 圆概率误差评价方法
近年来圆概率误差(CEP)被引入遥感图像的几何定位精度评价中来[22],其物理意义为样本中的被测点的偏差落在以CEP为半径的圆内的概率为,当为90%时,CEP即为CE90。
如果被测目标点的偏差服从正态分布,样本数据为目标点在沿轨方向几何定位误差的集合∋(1,2,…X),为目标点在垂轨方向几何定位误差的集合∋(1,2,…Y),则目标点几何定位误差集合(,)的联合概率密度分布如下

式中为,方向定位误差的相关系数。被测点个数为时,即样本容量,则式(4)中样本的相关系数为

当联合概率为90%时,则满足式(4)的CE90为
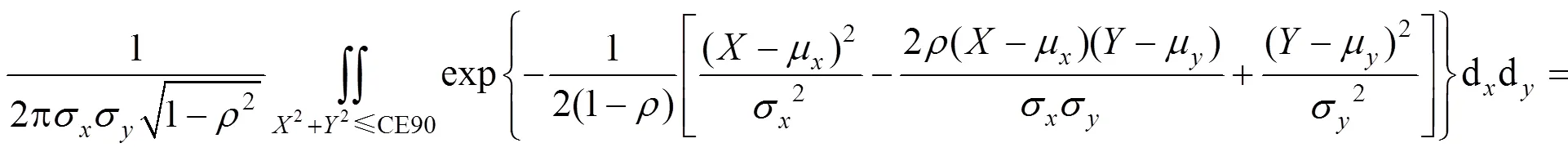
通过式(6)可知,CE90是样本满足置信概率为90%时的积分圆区域的半径大小,其意义为不大于CE90的样本数据占整个样本总体的90%。所以求出的CE90就是圆概率误差评价方法的平面几何定位精度。
2.3 传统中误差与圆概率误差评价方法的关系
通过分析式(1)~(6)可以得出,随着定位误差中含有的系统误差和随机误差的不同,两种不同几何定位精度评价方法有如下关系:
1)当几何定位精度中不含有系统误差时,且各方向上相互独立,即μ=0,μ=0,=0;置信概率为=68.26%时,记CE(68.26)为CE,则

式(7)表明,在相同置信概率的条件下,传统方法求得的平面几何定位精度与圆概率方法得出的结果不同。通过式(7)可以精确求出在置信概率为68.26%时的平面几何定位精度。
2)当几何定位精度中不含有系统误差时,且各方向上相互独立,即μ=0,μ=0,=0;置信概率为=90%时,
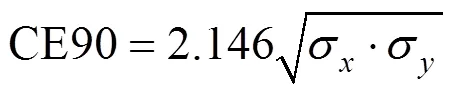
根据式(8)可知,在计算理想的外部几何平面定位精度时,由于系统误差被完全消除,卫星几何定位误差仅包括随机误差,因此利用上式可以将传统方法中求得的单一方向上的几何定位精度转化为圆概率误差方法中的平面定位精度。
3)当实际卫星几何定位误差服从正态分布,系统误差没有完全消除时,且在各个方向独立性不确定的情况下,即μ≠0,μ≠0,≠0;所以不能利用式(8)将单一方向上的几何定位精度直接转化为平面几何定位精度。此时需要通过式(6),利用数值积分的方法由σ,σ,μ,μ,求得CE90。求解方法如下:
则极坐标形式为

将μ,μ,σ,σ,代入式(9)中,通过数值积分方法,将CE90数值增大,当求出置信概率达到90%时,此时CE90的数值即为所求结果,即该条件下的外部几何平面定位精度。该评价方法考虑了随机误差和未消除的系统误差对精度的影响,因此更加准确可靠。
由以上推导可知,在平面几何定位精度的评价中,CE90的评价方法比传统中误差评价方法置信概率大。当系统误差完全被消除时,可通过式(8)直接计算CE90,完成对外部平面几何定位精度的评估。当系统误差没有完全被消除时,则不能直接通过简化公式计算CE90,需要通过式(9),利用数值积分的方法计算CE90,得出的结果包含了系统误差和随机误差对平面几何定位精度的影响。
3 仿真验证
将两组数据(每组数据包含100个满足正态分布的随机数)作为仿真图像中100个点在沿轨、垂轨方向上没有完全校正后的几何定位误差。定位误差中包括随机误差和系统误差,将数据求得的均值作为样本数据定位误差中的系统误差,将所有数据与对应均值之差作为随机误差。
按照前文所述,采用传统中误差评价方法对不含有系统误差的样本数据分别计算垂轨、沿轨、平面几何定位精度,采用圆概率误差评价方法对样本数据分别计算不含有系统误差的CE,CE90以及含有未完全消除系统误差的CE90。
图1为无系统误差的样本分布与CE90示意图,内圈到圆心区域表示中误差σ的置信区域,中圈到圆心区域表示CE置信区域,外圈到圆心区域表示CE90的置信区域,红色圆点位置为样本中每个点在沿轨和垂轨方向的定位误差。由图可知,在传统中误差评价方法中,由一维精度向二维精度合成时置信区间改变,置信概率不足68.26%。圆概率误差评价方法能准确计算置信概率为90%的几何定位精度,而且通过式(9)可以拓展计算任意置信概率下的几何定位精度。

图1 无系统误差的样本分布与CE90示意
图2为含系统误差的样本分布与CE90示意图。通过图1和图2中样本分布可以看出,由于系统误差的影响,样本分布明显偏离原点,但圆概率误差方法依然可以保证置信概率为90%。

图2 含系统误差的样本分布与CE90示意
表1为不同条件下不同评价方法得出的几何定位精度数据。首先,两种评价方法中,针对完全校正时的平面几何定位精度进行评价,结果2.53m大于1.71m,验证了CE90的置信概率是90%,置信区域大于传统方法的68.26%。其次,传统中误差法完全校正与没有完全校正条件下,几何定位精度数据相同,说明传统中误差法得到的评价结果不能反映系统误差对几何定位精度的影响,只能反映随机误差对定位精度的影响;而圆概率误差法评价两种条件下的几何定位精度,结果变化明显,没有完全校正的数据明显大于完全校正的数据,验证了系统误差对几何定位精度有影响,圆概率误差法对几何定位精度的评价结果包括了系统误差的影响。所以圆概率误差评价方法在评价二维几何定位精度时,比传统中误差评价方法更加适用。
表1 几何定位精度仿真结果

Tab.1 The calculation results of geometric location accuracy
4 结束语
本文从几何定位精度的概念和分类入手,分析了不同几何定位精度需要评价的内容,结合传统中误差评价方法和圆概率误差评价方法,得出不同的几何定位精度评价需要采用合适的评价方法进行评价才能得到可靠精确的评价结果:
1)当需要评价单一方向的几何定位精度时,采用传统的中误差评价方法可以快速简便地得到定位精度;
2)当需要评价二维几何定位精度时,圆概率误差评价方法比传统中误差评价方法更加准确可靠;
3)当评价外部几何定位精度时,应根据其几何校正的情况,选择合适的几何定位精度评价方法。
综上所述,根据对几何定位精度的分析,选择合适的几何定位精度评价方法,才能得到精确可靠的评价结果。
[1] 黄巧林, 姜伟. 高分辨率航天光学遥感器发展新思路研究[J]. 航天返回与遥感, 2007, 28(4): 48-50.HUANG Qiaolin, JIANG Wei. A Study of the New Direction of Space-borne Hi-resolution Optical Remote Sensor[J]. Spacecraft Recovery & Remote Sensing, 2007, 28(4): 48-50. (in Chinese)
[2] 夏中秋, 黄巧林, 何红艳, 等. 高分辨率光学遥感卫星几何链路定位精度分析[J]. 航天返回与遥感, 2016, 37(3): 111-119.XIA Zhongqiu, HUANG Qiaolin, HE Hongyan, et al. Analysis of Geolocation Accuracy of High Resolution Optical Remote Sensing Satellite Geometric Chain[J]. Spacecraft Recovery & Remote Sensing, 2016, 37(3): 111-119. (in Chinese)
[3] 唐新明, 谢俊峰, 张过. 测绘卫星技术总体发展和现状[J]. 航天返回与遥感, 2012, 33(3): 17-24.TANG Xinming, XIE Junfeng, ZHANG Guo. Development and Status of Mapping Satellite Technology[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(3): 17-24. (in Chinese)
[4] 阮宁娟, 庄绪霞, 李妥妥, 等. 空间光学遥感系统全链路仿真与分析[J]. 航天返回与遥感, 2013, 34(6): 36-43.RUAN Ningjuan, ZHUANG Xuxia, LI Tuotuo, et al. End to End Simulation and Analysis of Space Optical Remote Sensing System[J]. Spacecraft Recovery & Remote Sensing, 2013, 34(6): 36-43. (in Chinese)
[5] 张过. 线阵推扫式光学卫星几何高精度处理[M]. 北京: 科学出版社, 2016.ZHANG Guo. Line Push-broom Remote Sensing Satellite Geometry to Deal with High Precision[M]. Beijing: Science Publishing House, 2016.(in Chinese)
[6] 左德山. 提高高分辨率遥感影像系统定位精度技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2012.ZUO Deshan. Technical Research on The Improvement of Positioning Accuracy of High Resolution Remote Sensing Satellite Image System[D]. Harbin: Harbin Institute of Technology, 2012. (in Chinese)
[7] 余俊鹏. 高分辨率卫星遥感影像的精确几何定位[D]. 武汉: 武汉大学, 2009.YU Junpeng. Accurate Geometric Positioning of High Resolution Satellite Remote Sensing Imagery[D]. Wuhan: Wuhan University, 2009. (in Chinese)
[8] XIA Zhongqiu, HUANG Qiaolin, HE Hongyan, et al. Study on Geometric Performance Assessment Method of High Resolution Optical Remote Sensing Satellite Imagery[C]. Eighth International Symposium on Advanced Optical Manufacturing & Testing Technology, Suzhou: 2016, 9682: 96820N.
[9] XIA Zhongqiu, HUANG Qiaolin, HE Hongyan, et al. Analysis of High Resolution Two Line Array Camera Stereo Georeferencing Accuracy[C]. The 3rd International Symposium of Space Optical Instrument and Application, Beijing: 2016.
[10] 陈艺虾. 遥感图像几何定位精度评价方法研究[D]. 南京: 南京理工大学, 2013.CHEN Yixia. Research of Remote Sensing Imagery Geometric Location Accuracy Evaluation Method[D]. Nanjing: Nanjing University of Science and Technology, 2013.(in Chinese)
[11] 王任享, 王建荣, 胡莘. 天绘一号03星定位精度初步评估[J]. 测绘学报, 2016, 45(10): 1135-1139.WANG Renxiang, WANG Jianrong, HU Xin. Preliminary Location Accuracy Assessments of 3rd Satellite of TH-1[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(10): 1135-1139. (in Chinese)
[12] 王薇, 赵利平. GeoEye-1立体像对定位精度及其应用分析[J]. 遥感信息, 2012(1): 48-52.WANG Wei, ZHAO Liping. Analysis of Mapping Accuracy of GeoEye-1 Stereopair and Its Application[J]. Remote Sensing Information, 2012(1): 48-52. (in Chinese)
[13] 张佳栋, 李娜, 赵慧洁, 等. 采用SIFT特征的高光谱数据自动几何精校正[J]. 红外与激光工程, 2013(9): 2414-2420.ZHANG Jiadong, LI Na, ZHAO Huijie, et al. Automatic Geometric Precision Correction of Hyperspectral Data Based on SIFT feature[J]. Infrared and Laser Engineering, 2013(9): 2414-2420. (in Chinese)
[14] 盛庆红, 肖晖. 卫星遥感与摄影测量[M]. 北京: 科学出版社, 2015.SHENG Qinghong, XIAO Hui. Satellite Remote Sensing and Photogrammetry[M]. Beijing: Science Publishing House, 2015.(in Chinese)
[15] 张伍, 陆春玲. 推扫成像遥感卫星图像定位精度分析与设计[J]. 航天器工程, 2007, 16(7): 6-11.ZHANG Wu, LU Chunling. Design and Analysis of Determining the Image Position Error of Push-broom Remote Sensing Satellite[J]. Spacecraft Engineering, 2007, 16(7): 6-11. (in Chinese)
[16] 周楠, 何红艳. 星载线阵遥感器在轨几何外检校技术研究[J]. 航天返回与遥感, 2016, 36(5): 111-118.ZHOU Nan, HE Hongyan. Research of Geometric Exterior Calibration of Space-borne Linear Array Sensor[J]. Spacecraft Recovery & Remote Sensing, 2016, 36(5): 111-118. (in Chinese)
[17] LIGHT D L. Characteristics of Remote Sensors for Mapping and Earth Science Applications[J]. Photogrammetric Engineering & Remote Sensing, 1990, 56(12): 1613-1623.
[18] GRUEN A, KOCAMAN S, WOLFF K. Calibration and Validation of Early ALOS/PRISM Images[J]. The Journal of the Japan Society of Photogrammetry and Remote Sensing, 2007, 46(1): 24-38.
[19] 王建荣, 王任享, 胡莘. 卫星影像定位精度评估探讨[J]. 航天返回与遥感, 2017, 38(1): 1-5.WANG Jianrong, WANG Renxiang, HU Xin. Discussion on Evaluation of Satellite Imagery Location Accuracy[J]. Spacecraft Recovery & Remote Sensing, 2017, 38(1): 1-5. (in Chinese)
[20] 金涛, 李贞, 李婷, 等. 提高光学遥感卫星图像几何精度总体设计分析[J]. 宇航学报, 2013, 34(8): 1160-1165.JIN Tao, LI Zhen, LI Ting, et al. System Design and Analysis for Improving Geometric Accuracy of High-resolution Optical Remote Sensing Satellite Image[J]. Journal of Astronautics, 2013, 34(8): 1160-1165. (in Chinese)
[21] 张伟, 曹广超. 浅析遥感图像的几何校正原理及方法[J]. 价值工程, 2011(2): 189-190.ZHANG Wei, CAO Guangchao. Discussion on Geometric Correction of Remote Sensing Images[J]. Value Engineering, 2011(2): 189-190. (in Chinese)
[22] 张乐, 李武周, 巨养锋, 等. 基于圆概率误差的定位精度评定办法[J]. 指挥控制与仿真, 2013, 35(1): 111-114.ZHANG Le, LI Wuzhou, JU Yangfeng, et al. Positioning Accuracy Evaluation Method Based on CEP[J]. Command Control & Simulation, 2013, 35(1): 111-114. (in Chinese)
(编辑:王丽霞)
Analysis on Geometric Positioning Accuracy Evaluation of Remote Sensing Satellite Image
TIAN Guoliang HUANG Qiaoling HE Hongyan XIA Zhongqiu
(Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China)
The geometric positioning accuracy of remote sensing satellite image is an important characteristic of satellite remote sensing capability for both ground and on-orbit assessments. The geometric positioning accuracy obtained by the traditional evaluation method cannot completely consider the locating ability of the remote sensing satellites. Therefore a more accurate evaluation method is needed for different geometric positioning accuracy. Firstly, in this paper the concept of geometric positioning accuracy was introduced, and then the difference between internal and external geometric positioning accuracy was analyzed. Secondly, the advantages and disadvantages of standard error and circular error were given. Finally, different geometric positioning accuracy evaluation methods were used to estimate the simulation data. The results showed that more accurate and reliable assessment results can be obtained by choosing the appropriate evaluation method of geometric positioning accuracy.
geometric location accuracy; root mean square error; circular error; evaluation method; space remote sensing
P207+.1
A
1009-8518(2017)05-0106-07
10.3969/j.issn.1009-8518.2017.05.013
田国梁,男,1987年生,中国空间技术研究院飞行器设计专业博士研究生。研究方向为空间光学遥感器总体设计。E-mail:tglmingbai@163.com。
2017-05-15
国家重大科技专项工程
