基于数字检校场的“天绘一号”卫星在轨几何定标

胡振龙 郑柯 张勇 陶鹏杰



基于数字检校场的“天绘一号”卫星在轨几何定标

胡振龙1郑柯1张勇2陶鹏杰2

（1 中国天绘卫星中心，北京102102）（2 武汉大学遥感信息工程学院，武汉430079）

为了提高“天绘一号”卫星在轨几何定标的效率和精度，文章提出一种利用数字检校场（数字正射影像和数字高程模型）、基于简化的卫星几何定位模型的在轨几何定标方法。该方法利用卫星影像与数字正射影像自动匹配得到同名点的平面位置、由数字高程模型获得高程位置，得到大量地面控制点，再基于简化内外方位元素误差补偿模型，利用多轨数据求解系统误差改正参数，实现了几何定标。精度检测表明，经过定标后，无控定位平面误差由初始约100m，提升至10.5m（一倍中误差）；基于内方位定标结果，文章实现了基于虚拟线阵算法的高分影像子条带合成和多光谱配准，并实现了优于0.3像素的内部符合精度。

外方位元素 内方位元素 数字检校场 在轨几何定标 “天绘一号”卫星

0 引言

“天绘一号”是中国第一代传输型立体测绘卫星，先后共发射三颗，分别为“天绘一号”01星、02星、03星。该型号卫星携带了5m分辨率三线阵立体测绘相机（包括前、后、正视相机）、2m分辨率全色高分（由8条CCD子线阵组合而成）和10m分辨率多光谱三种相机，摄影幅宽优于60km；星上搭载GPS、星敏感器、陀螺仪三种轨道与姿态测量传感器。

卫星发射之前，一般都会对相关载荷进行实验室定标，以确定CCD线阵的相对、绝对位置和相机的主距、像主点位置、安装矩阵等系统参数。但卫星载荷入轨工作后，随着空间环境的变化，传感器可能发生变化，从而影响影像定位精度；文献[1]认为，国产遥感卫星搭载的定轨、测姿传感器，尤其是测姿传感器，存在较大系统误差，直接使用无法满足几何定位精度指标要求。与三线阵立体测绘相机不同，高分和多光谱相机没有按照测绘相机设计要求实现线阵推扫式无畸变成像，给数据处理带来了很大挑战。

为保证“天绘一号”卫星影像的测绘精度要求，需对卫星相机的内外方位进行高精度在轨几何定标，获取稳定可靠的几何定标参数，再通过轨道和姿态的测量值结合几何定标参数，获得精密外方位元素，并内插到每条扫描线影像的成像时刻，最后结合内方位元素实现卫星影像高精度几何定位。文献[2]认为，建立高精度地面检校场，并以此为基础对遥感测绘卫星的各种系统误差进行在轨几何检校，是高分辨率遥感卫星尤其是测绘卫星必须解决的首要问题。

传统在轨几何定标一般使用地面检校场进行，国内外的遥感卫星，比如ZY-3、SPOT-5、ALOS、IRC-1、IKONOS、GeoEye-1、QuickBird、WorldView等卫星均采用地面几何检校场进行几何定标和精度检测[3-6]。在轨几何定标的实现，首先要依据传感器的特点，建立适合的几何定位模型，通过地面控制点和对应的像点坐标建立共线方程，求解几何定位模型中的系统误差补偿参数。近30年来，各国学者提出多种几何模型，包括经验模型、通用模型和严格模型[7-11]。文献[12]中提出线阵推扫通用模型与相机成像的物理原理一致，被广泛应用于各高分遥感卫星定位。王任享等人采用EFP（等效框幅相片法）全三线阵光束法平差，利用地面几何检校场，求解“天绘一号”卫星三线阵相机的几何定标参数，实现了平面10m、高程6m（1倍中误差，后文简称1σ）的无地面控制点定位[13-19]，满足全球1∶5万地形图测绘精度要求。

传统几何检校场需依据不同卫星的传感器类型、相机分辨率、场地地形、地面覆盖、天气情况制定建设方案，建设成本较高，周期很长，重用性较差。在检测定标作业过程中，非常依赖人工作业，效率很低。

本文提出了一种基于数字正射影像（DOM）和数字高程模型（DEM）的几何定标方法，该方法使用现有地理信息数据成果（本文称作“数字检校场”），同时采用计算机自动点匹配取代人工量测，节约了几何检校场建设成本的同时，大大提高了作业效率。

1 TH-APGS系统简介

“天绘”高级影像产品生成系统TH-APGS（Tianhui Advanced Products Generating System），是为了满足“天绘”影像基础数据生产、应急测绘保障、高级产品快速生成等需求，研发的新一代全自动地面处理系统，其功能包含了原始数据到1B级产品生成的全部流程，包括：影像预处理、在轨几何定标、基于虚拟线阵算法的影像合成等关键技术，数据处理流程如图1所示。

图1 TH-APGS数据处理流程

TH-APGS自2014年4月投入使用以来，实现了“天绘一号”卫星影像基于网络环境的自动化、并行化、规模化处理，生产的1B产品（经过辐射校正和摄影测量处理、附带有理函数模型RPC参数）绝对定位精度高，且内部符合精度显著提升，用户反馈良好。该系统显著提升了1B产品生产效率，特别是解决了高分影像子条带拼接错位的问题。

在轨几何定标是实现高精度绝对定位和相对定位的关键。与业界普遍采用的地面检校场方案不同，TH-APGS系统采用了基于数字检校场和多轨数据统计分析的在轨几何定标技术，实现了与传统几何检校场方案同等的定标精度，同时也大大提升了几何定标的作业效率，是该系统的核心技术支撑。

基于数字检校场的几何定标以地理信息数据为参考数据源，利用现有的数字正射影像和数字高程模型作为地面控制数据。其特点和优势有[20]：1）容易获取。国内外地理信息数据种类丰富，只要满足覆盖范围和精度要求，都可利用其构成数字检校场，节约成本。2）效率高。使用计算机自动点匹配取代传统人工量测，极大提高作业效率。3）精度高。单点精度量测可能偏低，但能发挥数量优势，大量的观测值能有效弥补单点量测精度低的劣势。

2 基于数字检校场的在轨几何定标

基于几何检校场的几何定标，需要对几何定位误差建立准确的几何模型，例如，相机安装矩阵偏差、焦距误差、感光探元线阵位置误差和物镜畸变误差等等。在控制点和像点量测精度都较高的前提下，可求解得到满意结果。但数字检校场所采用的参考数据精度不高，计算机自动点匹配包含大量的粗差观测值，若使用较复杂的误差改正模型，则可能因为模型参数强相关、观测值中粗差太多等因素而导致求解失败。因此，需对误差定位模型进行适当的简化并调整解算策略。

2.1 在轨几何定标的通用几何模型

光学卫星影像通用几何定位模型[12]可表示为

式中ECS为像点对应的地面点在地心地固坐标系下的坐标；()为卫星质心位置；F为像点坐标；F为像主点坐标；为内方位元素改正数；M为相机投影中心到卫星质心的偏心向量；M为相机到本体坐标系安置矩阵；P为本体系到协议天球系的转换矩阵，由姿态传感器测量获得；O为协议天球系到地心地固系转换矩阵，通过地球定向参数和岁差章动模型计算获得；Δ表示外方位误差补偿矩阵；为非0实数。

卫星入轨前，通过实验室定标等方法，对成像传感器（包括星、地相机）与卫星本体坐标系之间的静态安置矩阵和GNSS（全球导航卫星系统）天线相位中心偏心向量等参数进行量测；但卫星入轨后，因应力释放和空间工作环境变化等因素，实验室定标的结果可能发生较大变化，必须通过星上传感器观测值并参照地面控制点，对定标参数进行再次解算，消除系统定位误差。

由于各参数之间的相关性（例如，星相机与地相机的安装矩阵高度相关）、误差因素的复杂性，各误差源对应的系统误差项很难区分；再加上地相机视场角小，导致方程未知数之间强相关、求解病态等原因，实际工程中在轨几何定标必须将误差项简化，常用的策略有三类：1）忽略非主要误差项。对最终定位误差影响较小的观测量认为是真值，减少未知数个数，提高求解成功率；2）对相关项合并。将相关性较大的误差项合并成一个误差量，去除未知数相关性，防止法方程病态、迭代不收敛；3）内外方位元素分别求解。

在式（1）中，GNSS定轨精度较高（优于3m），相对于目标定位精度（平面10m，高程6m）[13-19]，可认为()没有误差；偏心向量M较小（不足1.5m），对定位影响可以忽略；星敏感器安装矩阵误差和相机安装矩阵误差强相关，可以合并，式（1）最终简化为

式中 外方位误差补偿矩阵D是一个旋转矩阵，也称作偏置矩阵，直接的物理意义是相机安装矩阵的误差改正量，但在简化后的定位模型中，包含了星相机安装矩阵、地相机安装矩阵、地相机主光轴微小偏移等多个误差项，可吸收平差系统中线性部分；是内方位元素改正数，直接的物理意义为相机CCD线阵上每一个探元的焦平面坐标修正值，包含物镜畸变、探元安装位置误差、相机焦距误差等误差项，可吸纳平差系统中非线性部分。

2.2 数字检校场选择

数字检校场数据选择需要考虑四个方面的因素：

1）成本可控。检校场范围越大，定标可用数据源越多，效果越好，但要注意获取成本可控。

2）精度。外方位元素定标，选择的DOM精度和DEM精度应与几何定标后预定达到的无控定位相当；内方位元素定标所选择的DOM的相对精度中误差数值应小于像元分辨率。

3）分辨率。外方位元素定标中，DOM分辨率尽可能与被定标相机接近，如果DOM分辨率较高，可降分辨率重采样使之相同，以保证自动点匹配计算效率；内方位元素定标中，DOM分辨率应优于被定标相机。

4）地物。DOM覆盖区域应选择、纹理丰富、地物时相变化少的区域，地形尽量以平原为主。

以“天绘一号”卫星为例，定标后目标无控定位精度为平面10m和高程6m（1σ）。若采用数字几何检校场对外方位元素定标，DOM和DEM必须优于1∶5万比例尺的分辨率和精度要求。而高分相机分辨率为2m，1∶1万比例尺DOM分辨率为1m，相对精度优于2m，可满足高分相机内方位元素定标要求。

本文最终选取国内地区1∶5万DOM和国外地区其他公开DOM影像为主要数据源，高分相机的内方位元素定标采用了少部分国内地区1∶1万DOM。DEM数据使用国际上公开的STRM（Shuttle Radar Topography Mission），分辨率30m，高程精度在平原区域可达到6.5m（1σ）[22]。为了避免DEM误差造成的不利影响，内方位元素定标尽量选择地势平坦地区为几何定标场，摄影时近似垂直摄影。

2.3 内外方位元素定标

内外方位元素定标的流程如图2所示。首先以实验室定标结果为初始值，根据基础地理信息数据匹配同名点获得地面控制点，然后使用定向片法，对内外方位元素分别求解，以计算系统残差补偿参数，具体过程如图2所示：

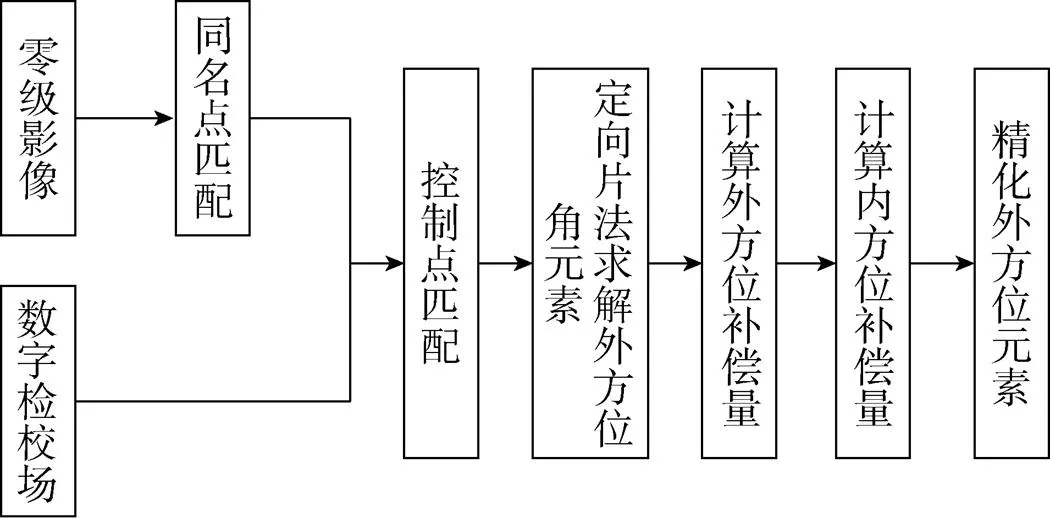
图2 外方位、内方位几何定标流程

几何定标的本质就是求解系统误差补偿参数，包括外方位误差补偿量Δ和内方位补偿量，可分为三个步骤：1）外方位初始定标；2）内方位元素定标；3）外方位元素定标精化。

（1）外方位元素初始定标

假设实验室内方位元素定标结果为真值，通过定向片法求解外方位元素；设时刻，定向片法求解的外方位元素旋转矩阵为，而此刻星上传感器测量结果为

那么时刻，外方位误差补偿矩阵Δ的计算公式为

对Δ矩阵按照航空摄影测量中的––转角系统分解，可得到三个独立分量转角，由于相机相对卫星本体的安装矩阵为近似单位矩阵，三个转角对应于卫星本体在轨道坐标系飞行的俯仰角、侧滚角和偏航角（如图3所示）。

图3 转角的示意

外方位初始定标，以一轨数据为基础，求解外方位误差补偿量的初步数值。在计算完整轨的Δ之后，以卫星所在位置的纬度为横轴，以对应时刻侧滚角改正数为纵轴，生成图4。

图4 侧滚角补偿量示意

由图4可知，不同纬度（或沿轨方向）对应的侧滚角补偿量计算结果略有不同，波动范围约0.002°，补偿量理论上应为常数，出现波动现象的原因是姿态传感器和地理信息数据都存在误差等因素。取整轨均值，即可得到侧滚角补偿量初值，俯仰及偏航两个方向的初值同理计算，侧滚、俯仰和偏航计算结果分别为：-0.007 97°、-0.008 13°和0.016 46°。

（2）内方位元素定标

设传感器测量加上外方位系统误差补偿后的外方位元素为真值，将像点对应的物方坐标投影到像平面上（认为实验室定标的相机焦距和像主点位置为真值），投影得到的像点坐标必然与该像点对应探元实验室定标位置存在明显差异，这个差异称作探元的内方位残差。

将所有匹配控制点像点残差投射到坐标平面，探元编号为横轴，残差量为纵轴，形成残差点云。图5为多光谱蓝波段像点残差点云。

（a）x方向残差点云（a）Residual point cloud on x direction（b）y方向残差点云（b）Residual point cloud on y direction

设CCD探元在成像焦平面连续排布，那么探元在焦面位置的偏差（即改正量）也应连续，故改正量可用连续曲线表达。图5中，点云残差聚集在改正曲线周围，在剔除了粗差值后，采用二次曲线拟合残差改正曲线，和方向（列方向和行方向）分别拟合，得到两个方向的残差改正函数。例如，方向改正函数Δ为：

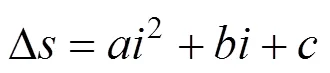
式中为探元列号；、、是拟合得到的系数。同理，可得到方向的改正函数Δ。

那么对任意一个CCD探元，设其实验室定标位置为（x,y），则内方位元素定标后的位置（x′,y′）为

排除观测异常值后，二次曲线拟合的中误差约为0.3像素。由于误差主要来自于像点匹配误差和参考数据误差，故定标实际精度应高于0.3像素。

理论上只要观测点足够多，残差点云必然聚集在一条残差曲线上，但某些情况下可能出现残差点多线聚集现象，原因是不同区域的DOM可能存在不同区域性系统误差。一旦出现这种现象，需对参考数据进行检核，剔除不符合要求的数据。对多光谱相机的内方位元素定标，可采用定标后的全色影像为参考影像来解决该问题。

（3）外方位元素定标精化

相比内方位元素，外方位元素求解结果受到的不确定影响因素较多，例如DOM和DEM精度、图像成像品质、低频误差、姿态传感器工作状态等因素，求解可靠的外方位元素改正数，不能依据单轨数据的计算结果，而必须利用多轨数据、多区域数据综合求解。为了防止与时间相关的低频误差的影响，多轨数据的摄影时间间隔不能太大。

以求解的内方位定标结果为真值，利用外方位初始定标同样的方法，求解多轨数据的补偿角矩阵，得到的结果（自动删除大粗差）如图6所示。

图6 多轨数据外方位元素补偿

将明显的粗差点剔除后，取所有轨平均值为最终结果：侧滚、俯仰和偏航方向的补偿量分别为–0.007 87°、–0.008 12°和0.017 83°。卫星飞行轨道高平均500km，而影像幅宽为60km，可推算三个方向对应地面的误差为68.7m、70.9m和9.3m，可知未经几何定标的情况初始定位误差为100m。分析了三个月超过100轨影像，外方位元素补偿角波动的中误差约为0.001°，换算到地面残差约为9m，可推测无控定位条件下平面中误差约为9m。

3 定标结果检测

要评价在轨几何定标的实际效果，一般通过产品定位精度测试来检测，包括绝对定位精度和内部符合精度两个方面。

1）绝对精度。利用野外控制点对三线阵模型前方交会同名点进行误差检核。

2）内部符合精度测试。检测影像内部畸变大小，是相对定位精度的反映。对2m分辨率全色高分影像，还需要对虚拟线阵算法合成CCD子线阵影像的效果进行测试[21-22]，评价有两种方法：①通过目视检查子片之间的重叠部分是否存在影像拼接错位。②通过大量的高精度控制点对影像进行定向平差，通过分析像点残差，检查影像内部畸变的大小和分布情况，即内部符合精度测试。

3.1 绝对定位精度检测

采用了172个野外控制点检测，影像覆盖情况和控制点的位置随机选择。误差检测平面CE90（Circle Error 90，圆误差置信度90%）为16.30m，高程LE90（Line Error 90，线误差置信度90%）为9.78m（图7）[24-25]，换算为1倍中误差为平面10.5m，高程5.96m，与文献[19]采用基于几何检校场的定标结果（平面10m、高程6m）相当。

图7 绝对定位精度检测结果

3.2 虚拟线阵算法的实现与拼接误差估算

虚拟线阵算法实现的子片拼接的精度，由三方面的条件决定：1）内方位元素定标精度；2）物方高程模型精度；3）卫星平台传感器对相机外方位元素（位置和姿态）测量精度。其中，条件1）与内方位元素定标精度密切相关，条件2）与采用的数字高程模型精度和绝对定位精度相关，因此，虚拟线阵算法实现必须以高精度几何定标为基础，同时对拼接后影像的精度检测也是几何定标效果的评价。

“天绘一号”高分相机，焦距约为2.1m，焦面上共安装了8个子片线阵，每个线阵4096个探元，成“品”字形交错排布。图8中实线为CCD探元位置，列排线阵之间的距离约为1.8cm（用表示）。

图8中，虚拟线阵的位置用虚线标示。虚拟线阵算法采用反解法，计算过程为：虚拟线阵位置（p，p）的虚探元通过共线方程，投影到参考DEM上，得到三维坐标（p，p，p），再通过共线方程投影到实际探元位置（p′，p′）。在建立的虚拟影像像点位置（p，p）与实际影像（p′，p′）的坐标对应关系后，通过重采样可生成虚拟线阵合成影像。多光谱相机各波段分线阵平行排布在同一个焦面上，波段间配准也能采用虚拟线阵算法实现：将分波段平行排布的子线阵重投影到一条相互重合的虚拟线阵上。

图8 探元在焦面上排布

图9 虚拟探元和实探元几何对应关系

设内方位元素定标后无误差，虚探元与实探元位置对应的精度取决于像点对应地物高程精度。像点位置误差为[26]：

式中 Δ为像点对应地物高程误差；为像元分辨率；为线阵之间的距离；为相机焦距。

参考DEM选用SRTM DEM，分辨率为30m，标称高程精度优于16m。设地形坡度小于45°，设无控定位精度优于50m，可推算地面高程误差不超过66m，平面位置误差和DEM高程误差引起的相邻线阵之间的拼接误差不超过0.3像素。将多光谱相机焦距、分辨率和线阵波段之间最长距离代入式（7），可推算多光谱波段之间配准误差应优于0.1像素。

3.3 内部符合精度检测

对高分辨影像进行子条带拼接错位检查，人工检查1 000景，未发现错位现象；多光谱影像各波段配准良好；采用1∶1万航空影像空三加密点，对高分影像、三线阵和多光谱影像进行内部符合精度检测，精度均优于0.3像素。

绝对定位精度和内部符合精度检测的结果证明：本文采用基于数字检校场的在轨几何定标，对高分、三线阵和多光谱相机的几何定标都适用，精度符合预期。

4 结论

本文基于数字检校场实现了“天绘一号”卫星内外方位几何定标，精度检测结果表明，外方位定标将初始定位100m左右的误差消减到10.5m，高程精度5.96m；内部符合精度优于0.3像素，高分和多光谱影像内部畸变基本消除，符合测绘产品要求。与传统的基于地面检校场的几何定标方法相比，基于数字检校场的在轨几何定标方法具备精度高、效率高、成本低等优势，不但实现了高精度的绝对和相对定位，还提升了作业效率，节省了几何检校场建设成本。

[1] 袁修孝, 曹金山. 高分辨率卫星遥感精确对地目定标位理论与方法[M]. 北京: 测绘出版社, 2012: 17-19. YUAN Xiuxiao, CAO Jinshan. Precise Location Theory and Method of High Resolution Satellite Remote Sensing[M]. Beijing: Surveying and Mapping Publishing House, 2012: 17-19. (in Chinese)

[2] 张永生, 刘军, 巩丹超, 等. 高分辨率遥感卫星应用——成像模型、处理算法及应用技术[M]. 第二版. 北京: 测绘出版社, 2014: 66-80. ZHANG Yongsheng, LIU Jun, GONG Danchao, et al. Application of High Resolution Remote Sensing Satellite--imaging Model, Algorithm and Application[M]. 2nd ed. Beijing: Surveying and Mapping Publishing House, 2014: 66-80. (in Chinese)

[3] RADHADEVI P V, MÜLLER R, D′ANGELO P, et al. In-flight Geometric Calibration and Orientation of ALOS/PRISM Imagery with a Genric Sensor Model[J]. Photogrammetric Engineering & Remote Sensing, 2011, 75(5): 531-538.

[4] HELDER D, COAN M, PATRICK K K, et al. IKONOS Geometric Characterization[J]. Remote Sensing of Environment, 2003, 88: 69-79.

[5] DIAL G, BOWEN H, GERLACH F, et al. IKONOS Satellite, Imagery, and Products[J]. Remote Sensing of Environment, 2003, 88(1-2): 23-36.

[6] BRETON E, BOUILLON A, GACHET R, et al. Pre-flight and in-flight Geometric Calibration of SPOT5 HRG and HRS Images[C]. Proceedings of ISPRS Commission I, Denver Colorado, 2002.

[7] FRASER C S, HANLEY H B. Bias Compensation in Rational Functions for Ikonos Satellite Imagery[J]. Photogrammetric Engineering & Remote Sensing, 2003, 69(1): 53-58.

[8] ZHANGY J, LU Y H, WANG L, et al. A New Approach on Optimization of the Rational Function Model of High-Resolution Satellite Imagery[J]. IEEE Transactions on Geoscience & Remote Sensing, 2012, 7(50): 2758-2764.

[9] KIM T, DOWMAN I. Comparision of Two Physical Sensor Models for Satellite Images: Postion-rotation Model and Orbit-attitude Model[J]. The Photogrammetic Record, 2006, 21(114): 110-123.

[10] MICHALIS P, DOWMAN I. A Generic Model for Along-track Stereo Sensors Using Rigorous Orbit Mechanics[J]. Photegrammetric Engineering & Remote Sensing, 2005, 74(3): 303-309.

[11] TEO T A. Bias Compensation in a Rigorous Sensor Model and Rational Function Model for High-resolution Satellite Images[J]. Photogrmmetric Engineering & Remote Sensing, 2011, 77(12): 1211-1220.

[12] WESER T, ROTTENSTEINER F, WILNEFF J, et al. Development and Testing of a Generic Sensor Model for Pushbroom Satellite Imagery[J]. The Photogrammetric Record, 2008, 23(123): 255-274.

[13] 王任享. 三线阵CCD影像卫星摄影测量原理[M]. 北京: 测绘出版社, 2006. WANG Renxiang. Three-line Array CCD Imaging Satellite Photogrammetry Theory[M]. Beijing: China Mapping Publishing House, 2006. (in Chinese)

[14] 王任享, 胡莘, 王新义, 等. “天绘一号”卫星工程建设与应用[J]. 遥感学报, 2012, 16(增刊): 2-5. WANG Renxiang, HU Xin, WANG Xinyi, et al. TH-1 Project Construction and Application[J]. Journal of Remote Sensing, 2012, 16(sl): 2-5. (in Chinese)

[15] 王任享. 天绘一号卫星无地面控制点摄影测量关键技术及其发展历程[J]. 测绘科学, 2013, 38(1): 5-7. WANG Renxiang. Day Painted First Satellite Photogrammetry without Ground Control Point Key Technology and its Development[J]. Science of Surveying and Mapping, 2013, 38(1): 5-7. (in Chinese)

[16] 王任享, 王建荣, 胡莘. LMCCD相机影像摄影测量首次实践[J]. 测绘学报, 2014, 43(3): 221-225. WANG Renxiang, WANG Jianrong, HU Xin. The First Practice LMCCD Camera[J]. Journal of Surveying and Mapping, 2014, 43(3): 221-225. (in Chinese)

[17] 王建荣, 王任享. “天绘一号”卫星无地面控制点EFP多功能光束法平差[J]. 遥感学报, 16(增刊): 112-115. WANG Jianrong, WANG Renxiang. TianHui-1 Satellite EFP Versatile Bundle Adjustment without Ground Control Point[J]. Journal of Surveying and Mapping, 2012, 16(sl): 112-115. (in Chinese)

[18] 王任享, 王建荣. 无地面控制点卫星摄影测量探讨[J]. 测绘科学, 2015, 40(2): 3-12. WANG Renxiang, WANG Jianrong. Discussion on Satellite Photogrammetry without Ground Control Point[J]. Journal of Surveying and Mapping, 2015, 40(2): 3-12. (in Chinese)

[19] 胡莘, 曹喜滨. 三线阵立体测绘卫星的测绘精度分析[J]. 哈尔滨工业大学学报, 2008, 40(5): 695-699. HU Xin, CAO Xibin. Accuracy Analysis of Survey and Mapping Three-line CCD Stereo Mapping Satellite[J]. Journal of Harbin University of Technology, 2008, 40(5): 695-699. (in Chinese)

[20] TAO P J, LU L P, ZHANG Y, et al. On-Orbit Geometric Calibration of the Panchromatic/Multispectral Camera of the ZY-1 02C Satellite Based on Public Geographic Data[J]. Photogrammetric Engineering & Remote Sensing, 2014, 80(6): 505-517.

[21] 张祖勋. 数字摄影测量与计算机视觉[J]. 武汉大学学报·信息科学版, 2014, 29(12): 1035-1039. ZHANG Zuxun. Digital Photogrammetry and Computer Vision[J]. Journal of Wuhan University Information Science Edition, 2014, 29(12): 1025-1039. (in Chinese)

[22] LUANA S, HOU X Y, WANG Y T. Assessing the Accuracy of SRTM DEM and ASTER GDEM Datasets for the Coastal Zone of Shandong Province, Eastern China[J]. Polish Maritime Research, 2015, 1(22): 15-22.

[23] JACOBSEN K. Calibration of IRS-1C Pan-camera[C]. ISPRS Workshop on Sensors and Mapping from Space, 1997.

[24] DOLLOFF J T, THEISSH J. The Specification and Validtion of Prediced Accuracy Capabilities for Commercial Satellite Imagery[C]. ASPRS 2014 Annual Conference, Louisville, Kentucky, 2014: 23-28.

[25] ROSS K. Geopositional Statistical Methods[R/OL]. [2017-7-18]. https://calval.cr.usgs.gov/wordpress/wp-content/uploads/ JACIE_files/JACIE04/files/1Ross16.pdf.

[26] 张过, 刘斌, 江万寿. 虚拟CCD线阵星载光学传感器内视场拼接[J]. 中国图象学报, 2012, 17(6): 696-701. ZHANG Guo, LIU Bin, JIANG Wanshou. Inner FOV Stitching Algorithm of Spaceborne Optical Sensor Based on the Virtual CCD Line[J]. Journal of Image and Graphices, 2012, 17(6): 696-701. (in Chinese)

（编辑：夏淑密）

On-orbit Geometric Calibration Based on Digital Calibration Field for TH-1 Satellite

HU Zhenlong1ZHENG Ke1ZHANG Yong2TAO Pengjie2

(1 TH Satellite Center of China, Beijing 102102, China) (2 School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China)

In order to improve the accuracy of TH-1 satellite image and efficiency of the geometric calibration, the article proposed a method of geometric calibration based on a simplified geometric model and digital calibration fields (digital orthophotos map and digital elevation models). In the method, the corresponding ground control points were obtained by auto-matching the raw image with DOM and fetching the height value by DEM, then the coefficients of error compensation model were solved by the simplified model. The test results demonstrated that the accuracy of position with no control points improved from worse than 100m to 10.5m (1 sigma). Based on the result of interior orientation calibration, the virtual line algorithm was implemented in the sub-chip image combination of the high resolution camera and multi-band camera, with the internal accuracy of better than 0.3 pixel.

external orientation element; internal orientation element; digital calibration field; on-orbit geometric calibration; TH-1 satellite

P236

A

1009-8518(2017)05-0086-10

10.3969/j.issn.1009-8518.2017.05.011

胡振龙，男，1975年生，2009年获武汉大学资源环境学院硕士学位，高级工程师。研究方向为高分辨率遥感卫星几何定标和三维重建。E-mail: 43530822@qq.com。

2017-02-27