雷达多视极化检测器性能对比分析

张鹏 张嘉峰 刘涛

(海军工程大学电子工程学院,武汉 430000)

雷达多视极化检测器性能对比分析

张鹏 张嘉峰 刘涛

(海军工程大学电子工程学院,武汉 430000)

雷达极化检测器性能对比分析可为极化检测器的工程设计提供重要参考,但目前针对其检测性能的评估理论仍不完善,尤其缺乏多视情形下的分析结果．文章以极化雷达多视协方差矩阵的复Wishart分布为基础,采用蒙特卡洛仿真与理论推导得到了7种经典极化检测器的多视检测性能曲线,并构建曲线下面积(Area Under Curve, AUC)指标对检测性能进行自动排序．仿真实验结果表明4视处理时的检测性能排序为:最优极化检测器>极化白化滤波器≈似然比检验>最佳能量检测器>极化匹配滤波器≈多视极化能量检测器>单通道检测器．理论推导结果表明,具有线性加权形式的极化检测器,其检测与虚警概率都具有两类等价的数学表达式,其中基于Gamma函数的表达式可用于快速计算出恒虚警检测门限．最后采用全极化合成孔径雷达实测数据,对上述结论进行了验证．

雷达极化;多视处理;检测性能;CFAR门限

引 言

过去二十年间,在极化合成孔径雷达(Polarimetric Synthetic Aperture Radar, POL-SAR)应用需求的强势牵引下,雷达极化检测理论得以迅猛发展,经典的雷达极化检测器包括最优极化检测器(Optimal Polarimetric Detector, OPD)、单位似然比检验(Identity Likelihood Ratio Test, ILRT)、极化白化滤波器(Polarimetric Whitening Filter, PWF)、极化匹配滤波器(Polarimetric Matched Filter, PMF)、能量检测器(Span Detector, SD)[1-10]等．上述极化检测器能够行之有效地改善雷达检测性能,针对其性能表现,文献[5, 10]进行了系统地对比分析,但他们的研究主要关注单视情形,但实际应用中,为抑制相干斑或数据压缩,常需要对极化数据进行多视处理．基于此,Novak L.M.提出了多视最优极化检测器、多视极化匹配滤波器[2],刘国庆则提出多视极化白化滤波器[7]．多视检测器一经提出便广泛应用于POL-SAR中,一个重要的原因在于其抑制相干斑的同时还能改善检测性能[8],那么多视极化检测性能如何评价?视数增加对极化检测性能影响程度如何?已有文献尚缺乏相关解答．此外,比较检测算法性能还需权衡其所需的先验信息、计算复杂度等,如何建立一套完整的评价体系以确定最佳的极化检测器类型与视数也有待研究．

本文首先将最佳能量检测器 (Optimal Span Detector, OSD)、单通道检测器(Single Channel Detector, SCD)以及ILRT检测量的构成推广至多视情形,且推导了不同名义视数下多视SD、多视OSD与多视SCD解析检测性能的两种表达形式,分别通过蒙特卡洛仿真和解析方法获取多视极化检测器的检测性能并予以分析．不同于单视情形,在分析多视极化检测性能时需要综合考虑处理视数的影响,包括视数对检测性能的影响以及视数增加必然引起的SAR分辨率损失[11],这涉及到如何衡量多视处理的影响与极化检测性能优劣的问题;针对检测性能评价问题,本文通过AUC指标、多视增益等指标综合评价了多视极化检测器．由于实际中协方差等先验信息未知,本文还基于协方差估计仿真了自适应多视极化检测性能．

1 多视极化雷达回波建模

极化雷达通过测量目标散射矩阵以获取目标全极化特征[3],但在单站互易媒介条件下,仅需测量三维散射矢量:

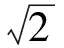
(1)

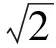
由于本文主要研究中、低分辨率条件下的极化雷达,目标极化散射回波可视为复高斯随机矢量

(2)

式中:XHHI、XHHQ分别代表HH通道同相和正交分量;散射矢量X的各分量XHH、XHV和XVV服从如下零均值复高斯分布:

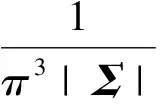
(3)

式中:|·|表示矩阵的行列式;上标H表示复共轭运算;Σ代表散射矢量X的协方差矩阵,由Σ=E(XXH)[5]得

(4)

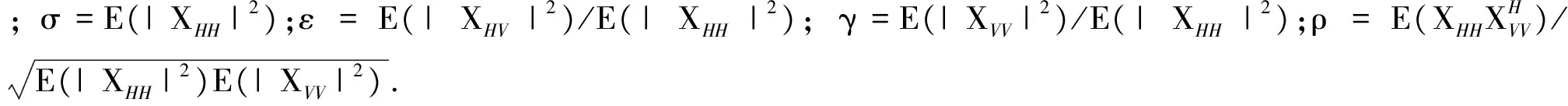
为进行数据压缩或者抑制相干斑噪声,通常需要在协方差矩阵域进行多视处理[8],L视处理的多视协方差可由散射矢量进行外积运算得到:

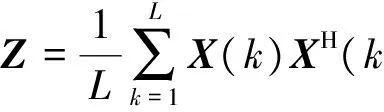
(5)

经L视处理的多视协方差矩阵Z服从复Wishart分布[7]:

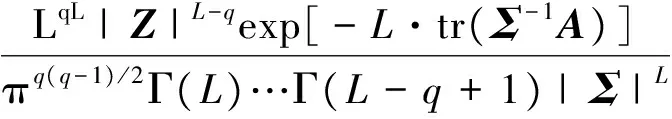
(6)

在式(6)所示的概率密度函数(Probability Density Function,PDF)中:q表示散射矢量的维数,本文取3;Σ代表多视处理后的协方差矩阵;Γ(·)为不完全Gamma函数,且有Γ(L)=(L-1)!

值得注意的是,在乘性噪声模型框架下,实际测得的极化雷达回波数据Y具有如下的形式[8]:

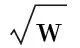
(7)

式中,w表示地物雷达散射截面积(Radar Cross Section,RCS)因子,本文假定杂波服从高斯分布且w取为1．此外,在进行数据仿真时假设杂波背景下目标的回波具有如下加性结构:

Xt+c=Xt+Xc.

(8)

由式(5)可知,杂波背景下目标散射回波的零均值协方差矩阵同样具有加性结构:

Σt+c=Σt+Σc.

(9)

2 极化检测器及其解析检测性能

本节在简要介绍四类典型多视极化检测器的基础上,将ILRT、OSD、SCD推广至多视,构造了多视ILRT、OSD、SCD检测量的数学表达式,推导了多视SD、OSD、SCD解析检测性能的两种表达形式,在与107次蒙特卡洛实验得到的性能仿真结果进行对比后验证了该推导结果的正确性．

2.1最优极化检测器(OPD)

由二元检测中最佳检测器的结构可知,判定目标出现的似然比检验形式为

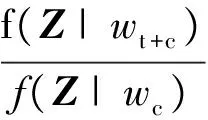
(10)

式中:先验概率f(Z|wt+c)由式(6)给出;TD为检测门限．由于多视处理时通常假定各视数据独立同分布,那么OPD似然比检测量可表示为

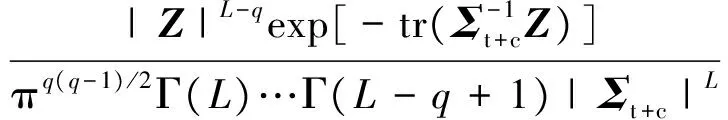
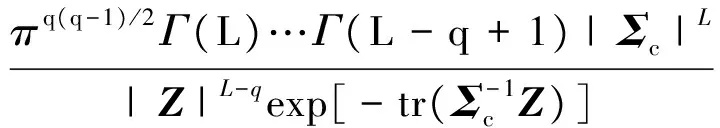
(11)

对式(11)化简,两端同时取对数可得m视OPD检验统计量为

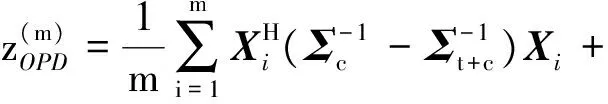
(12)

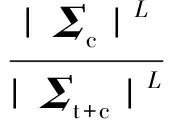
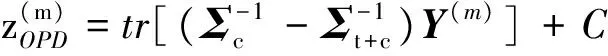
(13)

式中Y(m)表示m视协方差矩阵数据．OPD的检测、虚警概率的表达式都具有如下的形式[1-2]:

(14)

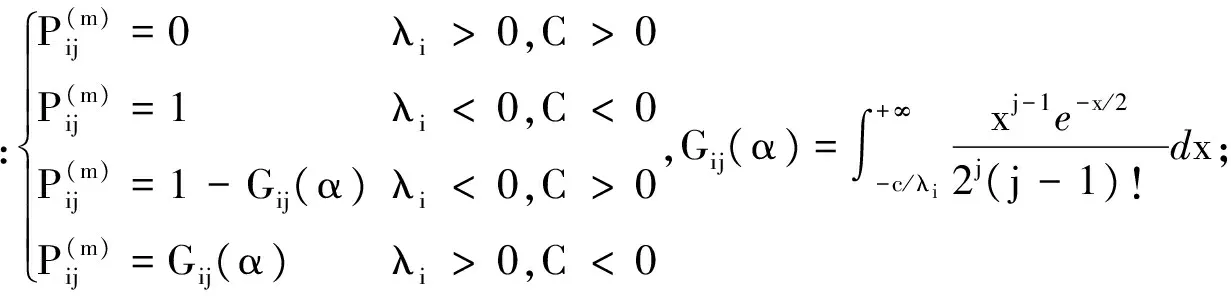
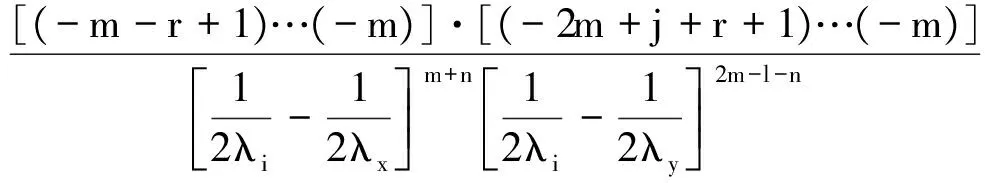
(15)

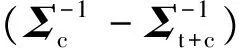
2.2单位似然比检验(ILRT)

对单视OPD稍加变形后即可得到ILRT,特点是采用可缩放的单位矩阵(Identity Matrix)代替OPD中的目标协方差矩阵,有

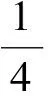
(16)

ILRT对数门限检验统计量为

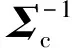
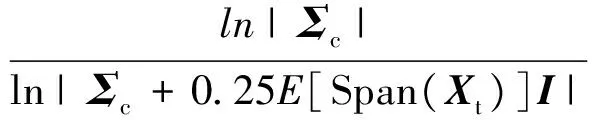
(17)

参考式(10)至式(13)所示的OPD检验统计量的推导方式,可以导出m视ILRT的检验统计量如下:

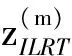
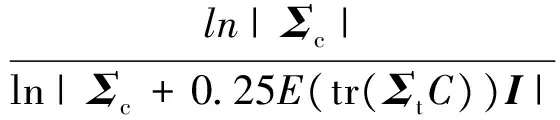
(18)

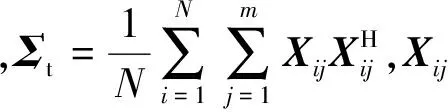
2.3极化白化滤波器(PWF)

作为一种次优极化检测器,PWF已被广泛使用,m视PWF的检验统计量[1]为

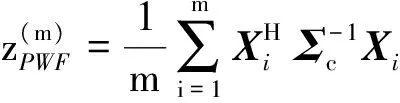
(19)

若采用迹运算表示,式(19)可记为

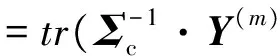
(20)

检测门限取T时,PWF虚警概率为[7]

(21)

式中,w1表示乘积噪声模型下杂波纹理因子．PWF检测概率为[7]

(22)

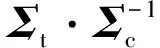
2.4极化匹配滤波器(PMF)

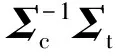
(23)

PMF的解析检测概率/虚警概率为

(24)

式中,σ=E(|hHX|2)=E(hHΣh)．

2.5几种典型能量检测器及其解析检测性推导

基本的SD利用矢量张成而不利用任何先验信息进行检测,所以,

z=|SHH|2+2|SHV|2+|SVV|2

=XHCX=XHGGHX

=|GHX|2=YHY.

(25)

式中:C=diag(1,2,1);G和GH是对C进行Cholesky分解所得．进而可以导出m视SD检验统计量:

(26)

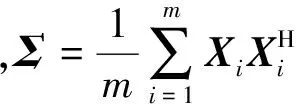
(27)

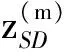
(28)

对式(28)进行一次广义积分即可得到PMF检测或虚警概率如下:

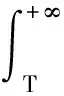
(29)

根据文献[16]中的积分结果

(30)

(31)

式(31)是通过级数展开得到的结果,事实上由式(28)、(29),还可得到

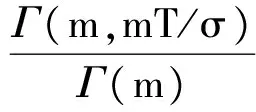
(32)

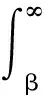
(33)

作为单视SD的一种改进形式,OSD不再采用常系数权值,而是利用杂波协方差关键参数εc、ρc、γc确定各极化通道能量加权系数,其检测量为

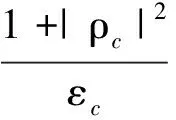
=XHDX．

(34)

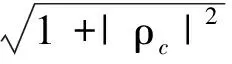
(35)

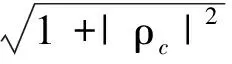
σ=E(|HHX|2)=E(HHΣH)．

SCD是一类特殊的极化检测器,其仅利用单个极化通道进行目标检测,一般采用线性共极化通道(HH极化):

(36)

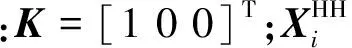
(37)

分析以上推导过程可以看出,无论是SD、OSD、SCD,其都可看成对散射矢量进行线性加权获得的检测量,因而在中低分辨率条件下,对散射矢量进行线性加权的极化检测器都具有式(31)、(32)所示的解析检测性能形式．

3极化检测性能对比分析及解析检测性能拟合效果

本节分别通过蒙特卡洛仿真和解析推导结果获取上述7种多视极化检测器的检测性能,采用AUC指标、多视增益对多视极化检测器比较分析,验证了解析推导结果有效的同时,提出了多视情形下SD、OSD、SCD、PWF实现恒虚警率(Constant False-Alarm Rate, CFAR)检测的新途径．检测场景通过表1所示目标与杂波的协方差关键参数确定．

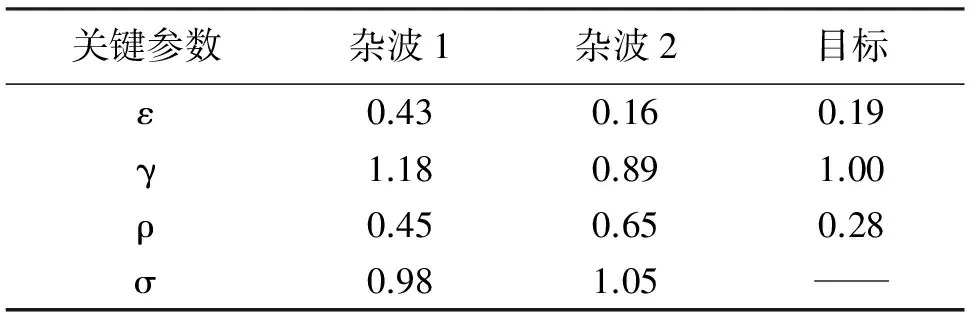
表1 典型目标与杂波的关键参数

注:表中关键参数参考文献[2]与文献[10]得到

定义目标杂波比(Target-to-Clutter Ratio, TCR)为目标与杂波能量期望的比值[14]:

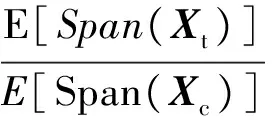
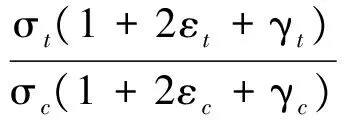
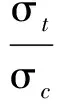
(38)

采用表1中杂波1与目标的关键参数组合进行多视极化回波仿真,进行107次多视极化检测的蒙特卡洛实验．分别设置Pfa=10-4、RTC=0 dB,则可得到4视的极化检测器检测性能曲线(检测概率-TCR曲线)和ROC曲线,如图1和图2所示．

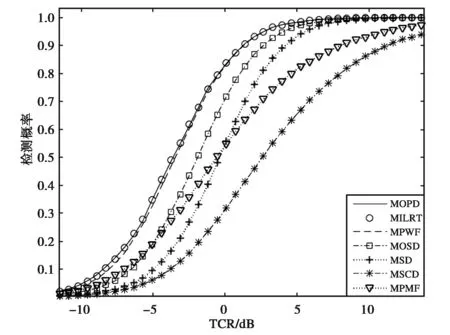
图1 理想检测概率随TCR变化曲线(4视,Pfa=10-4,图例 中的检测器缩写前的M代表多视,后文图例亦然)

图1表明:4视处理的条件下,OPD因其采用了最优的权值仍然表现出了最优的检测性能;在TCR的大部分实验区间内,PWF与ILRT的检测性能与OPD都十分接近;当TCR小于-5 dB时,PMF的检测性能紧随其后,而当TCR大于-5 dB时,OSD的检测性能开始优于PWF;当TCR大于0 dB以后,SD又将优于OSD;SCD因其仅仅利用了单极化信息,检测性能最次．因而,在4视条件下,检测性能排序为OPD>PWF≈ILRT>OSD>PMF≈SD>SCD．

为能简洁而又不失全面地分析多视极化检测性能可比较其ROC曲线,如图2所示．若虚警水平取为-30 dB,比较此水平下检测概率亦可得到以上排序结果．但需注意的是,OPD、ILRT、PMF需要获取目标的先验信息,故从工程实现的角度,PWF、OSD是性能较好的极化检测器,其次是SD与SCD．

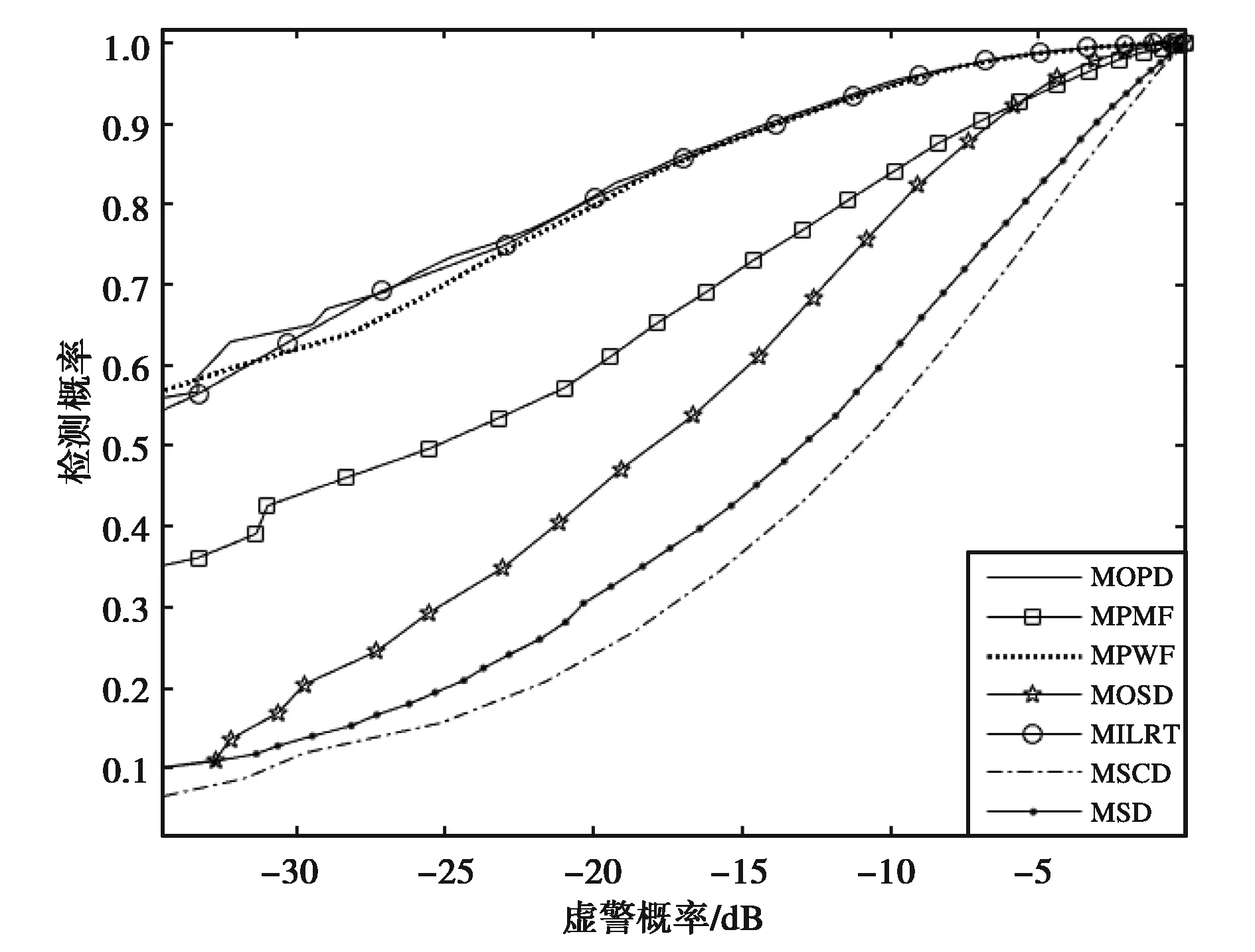
图2 不同检测算法的ROC曲线(4视,TCR为0 dB)

结合图3可知,TCR的提高自然会带来检测性能的改善,加之本文旨在研究视数对检测性能的影响,因此在后文的研究中,TCR设置为0 dB．

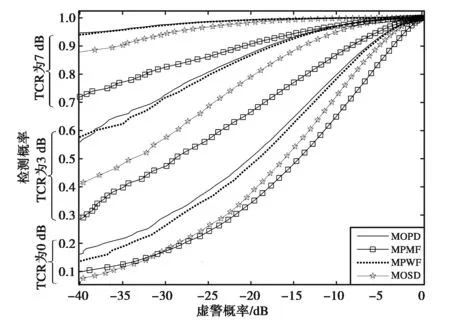
图3 ROC曲线随TCR的变化(4视)

对于极化检测器的ROC曲线而言,研究其在虚警概率区间内的积分(下面积)亦有实际的意义．借鉴医疗诊断实验效用评估中常采用的ROC的AUC指标[15],不妨将其应用于检测性能ROC曲线以评价检测性能优劣,且由于雷达常工作在低虚警水平,全虚警区间AUC没有实际参考价值,所以可以基于雷达常用的低虚警概率优选积分区间获得改进的AUC以客观评价检测性能．AUC计算时可采用非参数直接积分的方法,即通过ROC曲线有限组点迹估计其在特定虚警区间内的下面积,其值越大则说明检测性能越好．其视数极化检测器ROC曲线如图4所示.

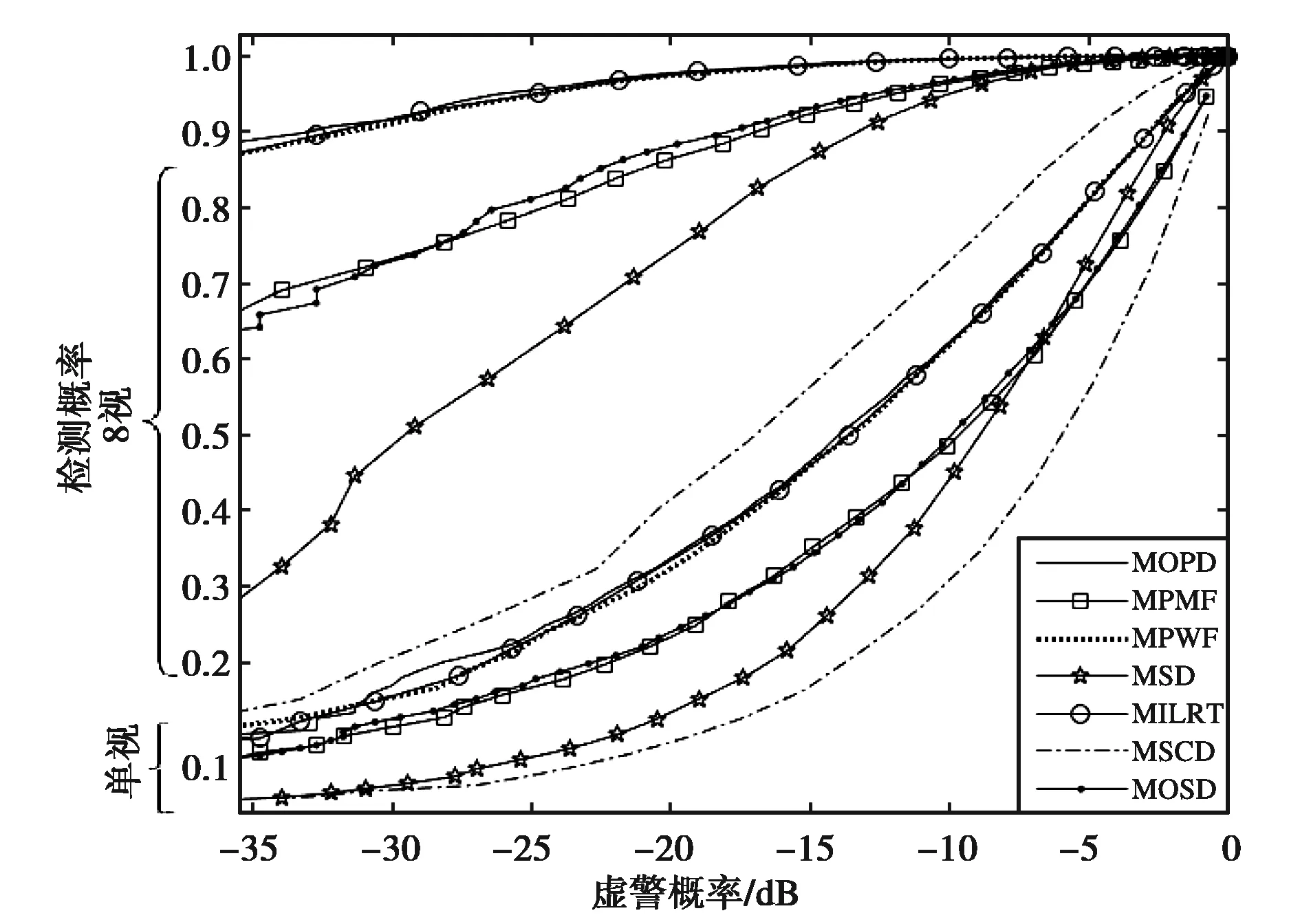
图4 ROC曲线随视数的变化

图4表明:视数增大时,同一虚警水平的检测概率会明显增加,这说明多视处理对检测性能的改善是有效的．若选取虚警区间为(10-5,10-2),可计算出不同视数和TCR条件下的多视检测器AUC指标与检测性能排序,结果如表2所示．

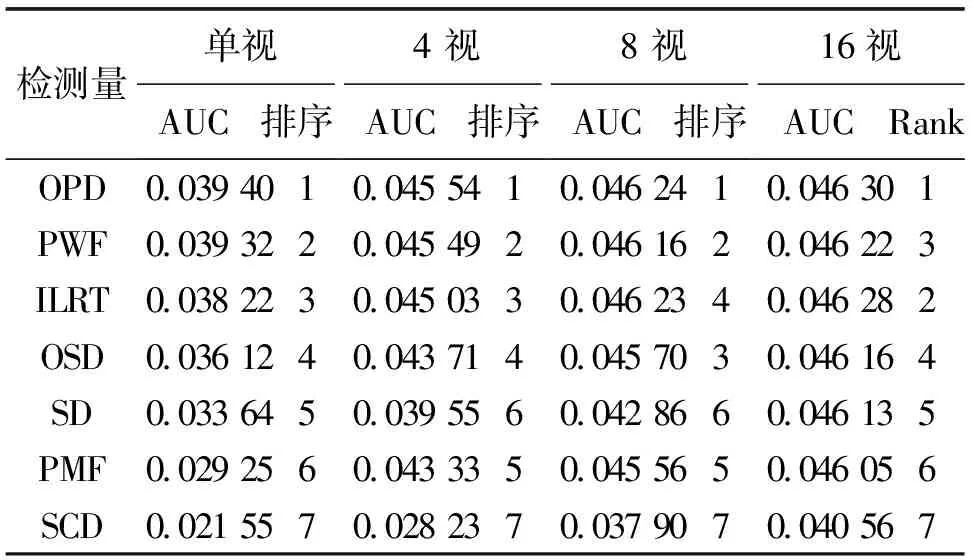
表2 多视极化检测器AUC指标与排序结果 (TCR为0 dB)

表2计算结果清晰直观地反映了不同视数下检测性能的排序．由表2可知,视数由单视向4视变化时,PMF的检测性能超越了SD的检测性能,这与前文通过4视检测性能曲线总结的结果一致．

图4说明多视处理明显地改善了极化检测性能,对于图中OPD而言,在TCR为0 dB、Pfa=-30 dB时,8视处理之后的检测概率相对于单视情形提高了9倍左右(约9.542 dB)．为了能够整体地衡量视数改变对检测性能的改善,不妨继续考虑特定虚警区间内检测概率的改善,基于AUC的定义,多视增益G(m)定义为

(39)

式中,AUC(m)、AUC(1)分别表示TCR确定的在特定虚警区间内的AUC指标,单视增益为0 dB．通过对AUC的计算可得TCR为0 dB、虚警区间为(10-5,10-2)时(即为(-50 dB,-30 dB))的不同视数的多视增益如表3所示．

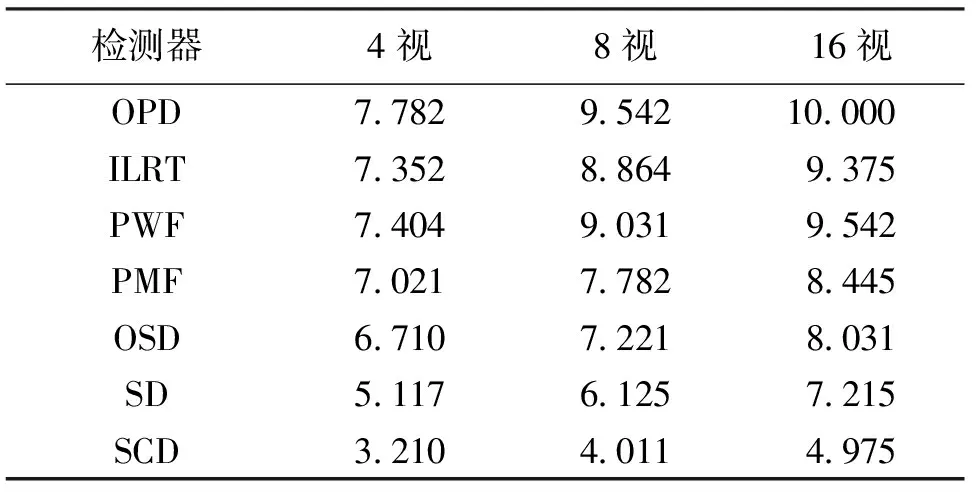
表3 不同多视极化检测器的多视增益 dB

比较不同视数的多视增益可见:4视处理已能使多数极化检测器获得7 dB左右的多视增益,就工程应用而言已可获得实际的效益;若一味增加视数,检测性能将不再提高那么明显,且由于多视处理是以牺牲分辨率为代价的,因而工程应用中多视极化检测器视数取4为好．由表3还可看出:视数增加时,单极化的SCD和不利用先验信息的SD检测性能改善较缓慢,即多视处理对这类检测器带来的“好处”小．

以上检测性能仿真均是在杂波协方差参数已知情形下进行的,但由于实际检测中通常不能事先预知,往往需要从测量的极化散射矢量数据中估计得到,参考文献[12]的估计方法有

(40)

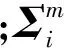
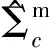
(41)

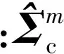
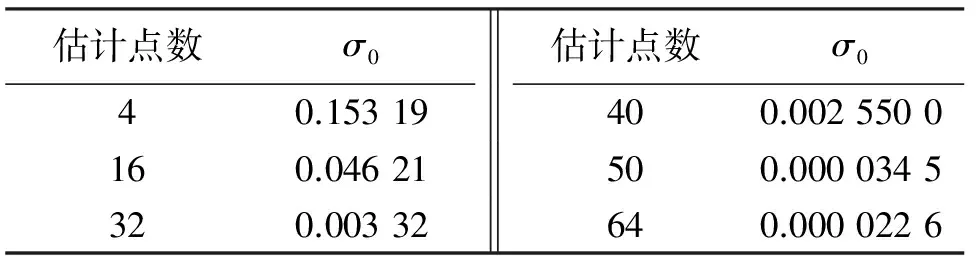
表4 不同估计点数零位元素估计方差

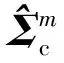
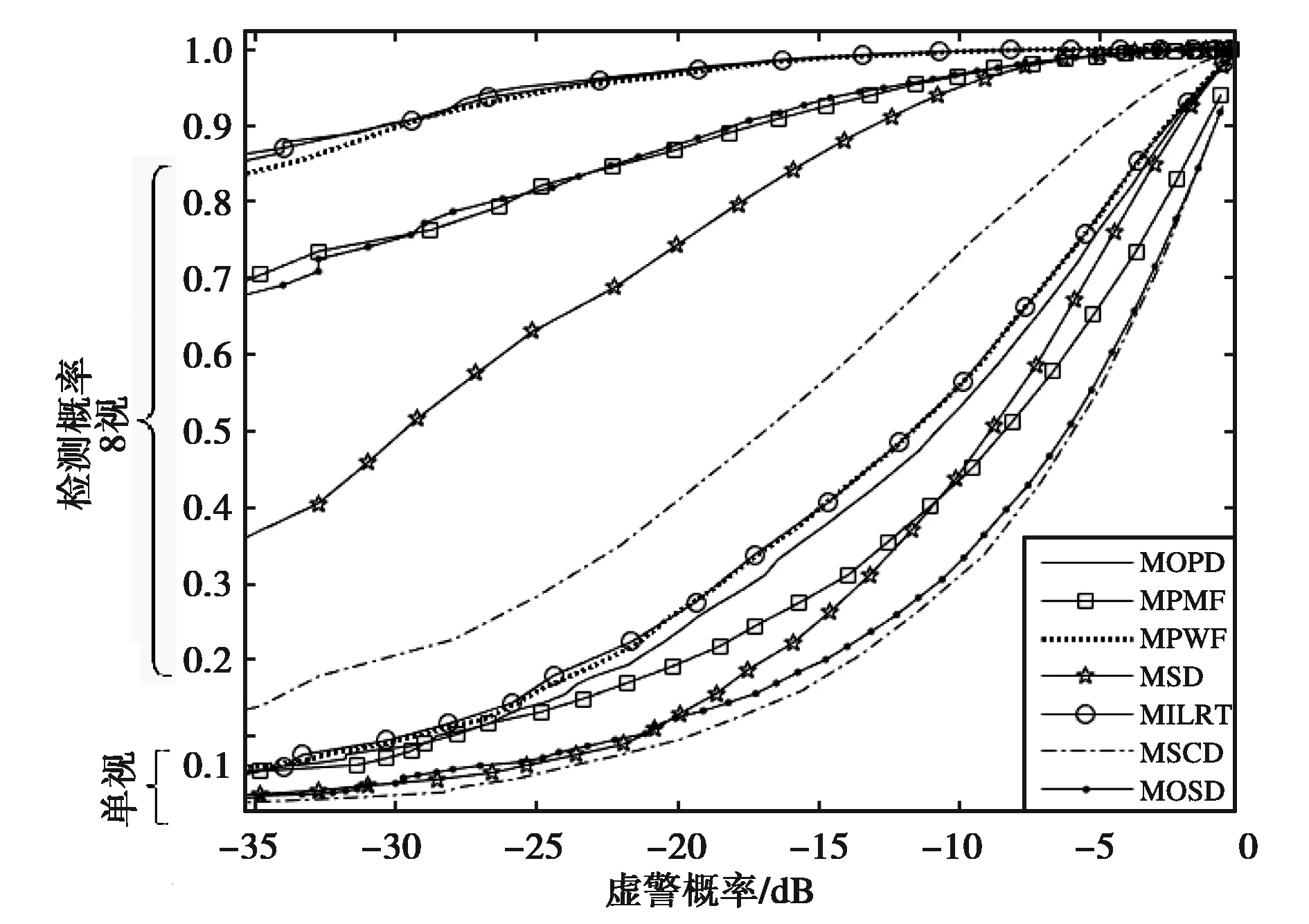
图5 采用16点协方差估计结果得到的多视检测器ROC

对比图4、图5可以发现:协方差矩阵估计点数对于SD这种不依赖先验信息的检测器影响较小;而对PMF这种综合利用统计先验信息的检测器影响较大．文献[10]指出,对于单视数据协方差矩阵估计时点数取64为好．对于4视数据协方差矩阵而言,当估计点数为16时可初步拟合预期检测性能;估计点数为64时可较好地拟合;估计点数取32即可满足需求．

图1至图5均为蒙特卡洛仿真得到的多视检测性能,仿真时间较长,快速获取检测性能则需通过解析方法,结合式(14)、(2)、(22)、(24)以及本文推导的式(31)、(32),设置TCR为0 dB,仍然采用表1所示的检测场景,可以得到图6所示的解析ROC,以及式(32)、(33)的拟合效果图7．

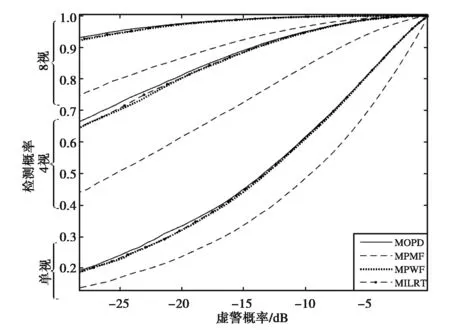
图6 不同视数下的解析方法计算得到的ROC曲线

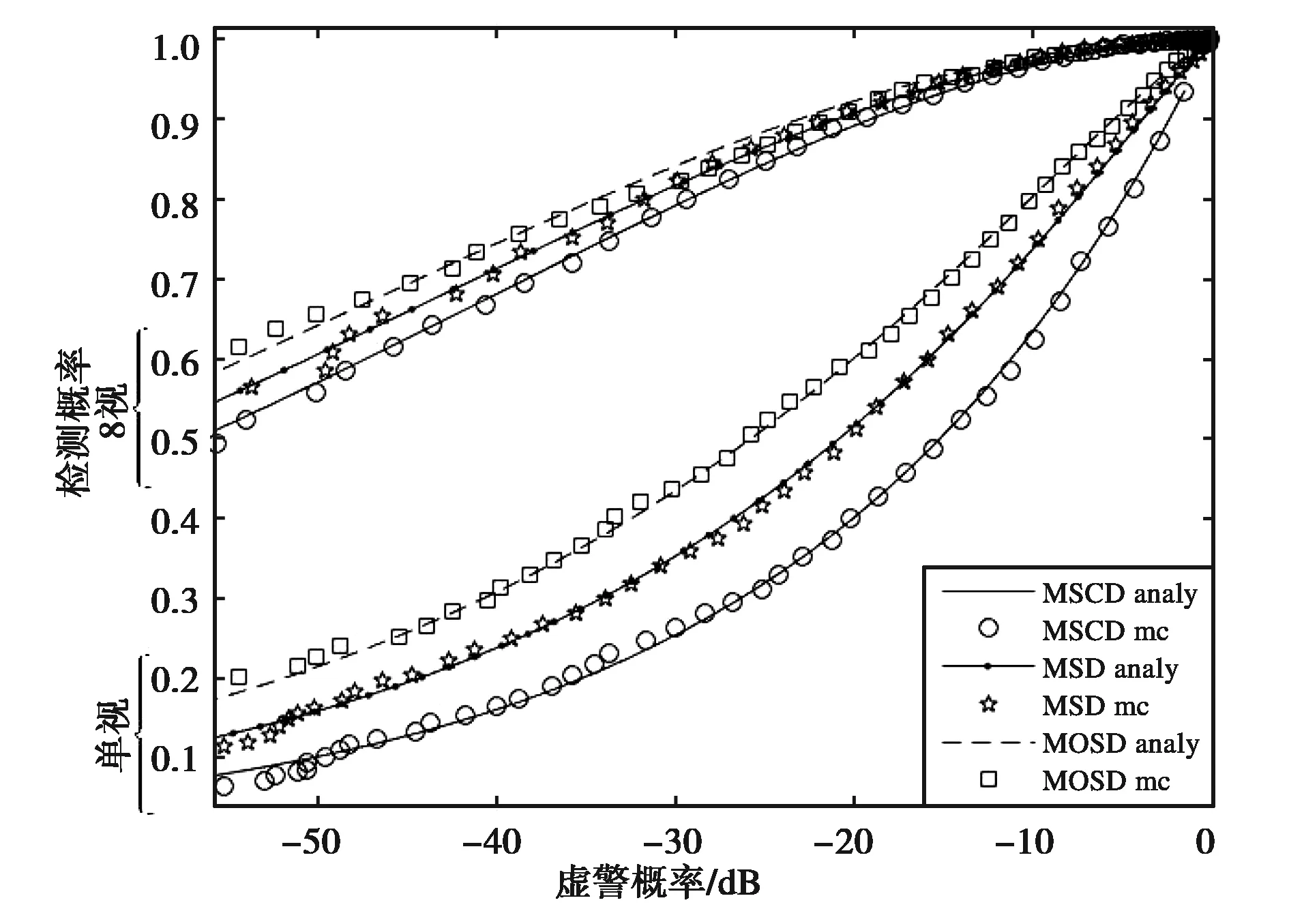
图7 不同视数下解析检测性能的拟合效果 (图例中的 ‘analy’ 代表解析结果,‘mc’代表蒙特卡洛仿真结果)

观察图7可见,解析检测性能结果与蒙特卡洛方法所得结果基本一致．由图7可得:不同视数条件下,本文推导的SD、OSD、SCD的解析检测性能与107次蒙特卡洛仿真结果吻合性较好,说明式(31)与(32)的推导结果是有效的．

虽然多视SD、OSD的检测性能不如多视OPD或PWF,但因其检测时所需的先验信息较少,故计算速度较快,适合一些需要快速计算的场合,为此基于式(31)和(32)反推出解析检测门限是有必要的．由推导过程可见,式(31)与(32)的物理本质是相同的,只是在数学表达形式上分别采用了级数求和与Gamma函数的方式,但式(32)的Gamma函数的表达形式使用时更加灵活,通过Gamma函数求逆可以得到式(33)所示的检测门限的表达形式．采用32点协方差估计,结合表1所示的检测场景并设置TCR为0 dB,可以估计出不同视数、不同虚警概率对应的检测门限,结果如图8所示．

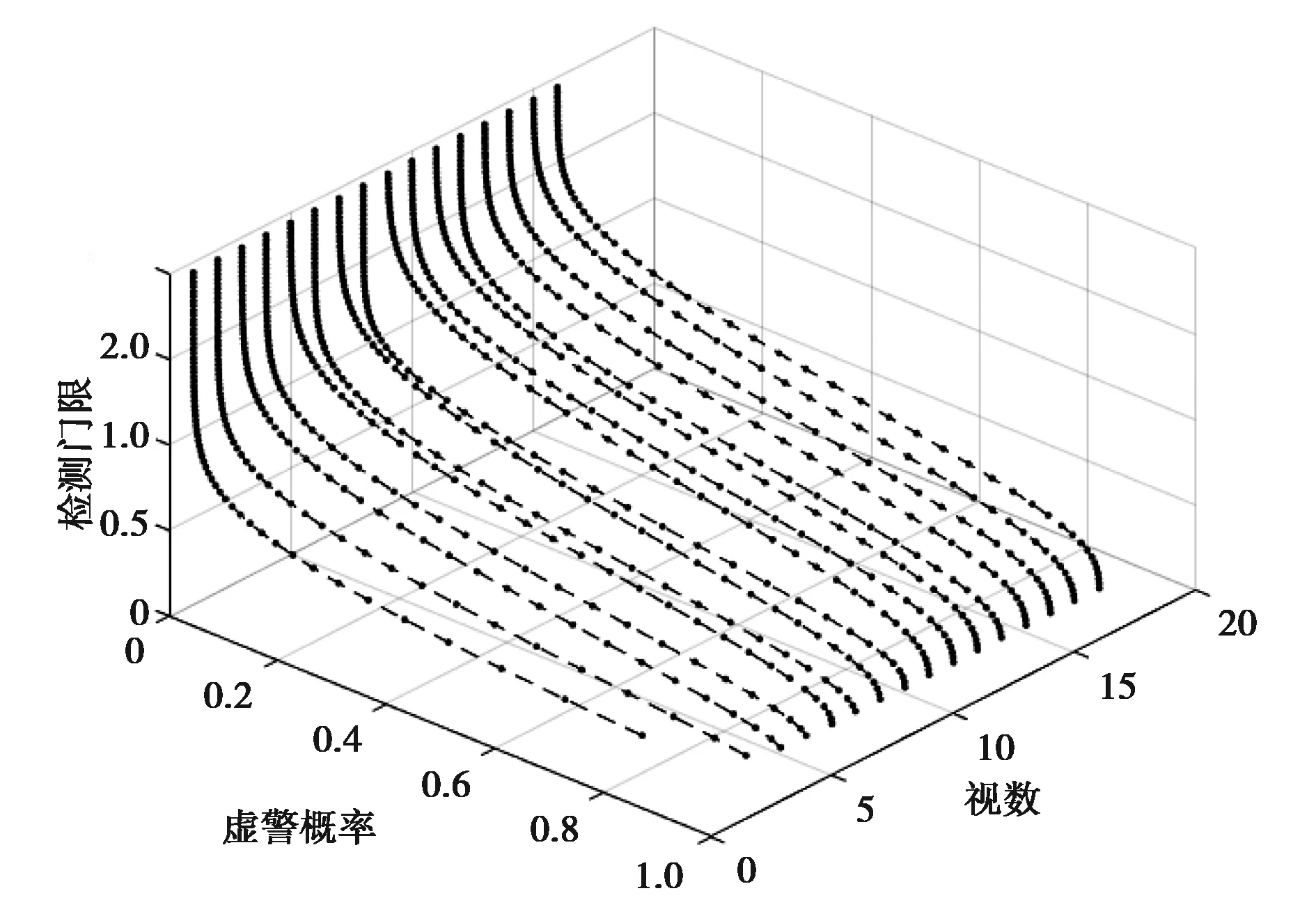
图8 基于32点协方差估计获取各视CFAR检测门限曲线

图8表明:在视数和TCR确定时,通过式(33)可以快速计算出检测门限,也就是说通过式(41)对杂波协方差进行估计后,针对不同视处理的极化检测器可快速计算出不同虚警水平的极化检测门限,且视数可以不是整数,这为线性加权类的极化CFAR检测提供了新的实现途径．

4 实测数据验证

前文基于理论推导和仿真实验对多视极化检测器的检测性能进行了对比分析,下面将采用实测数据对上述结果进行验证．

图9(a)所示为2000年美航局对日本玉野地区成像得到的全极化数据,选取图中A区放大后得到图9(b),该区图像尺寸为153行、96列,共14 688组像素数据．由图可见,A区中有两艘舰船目标,下面主要针对该区域数据进行验证．

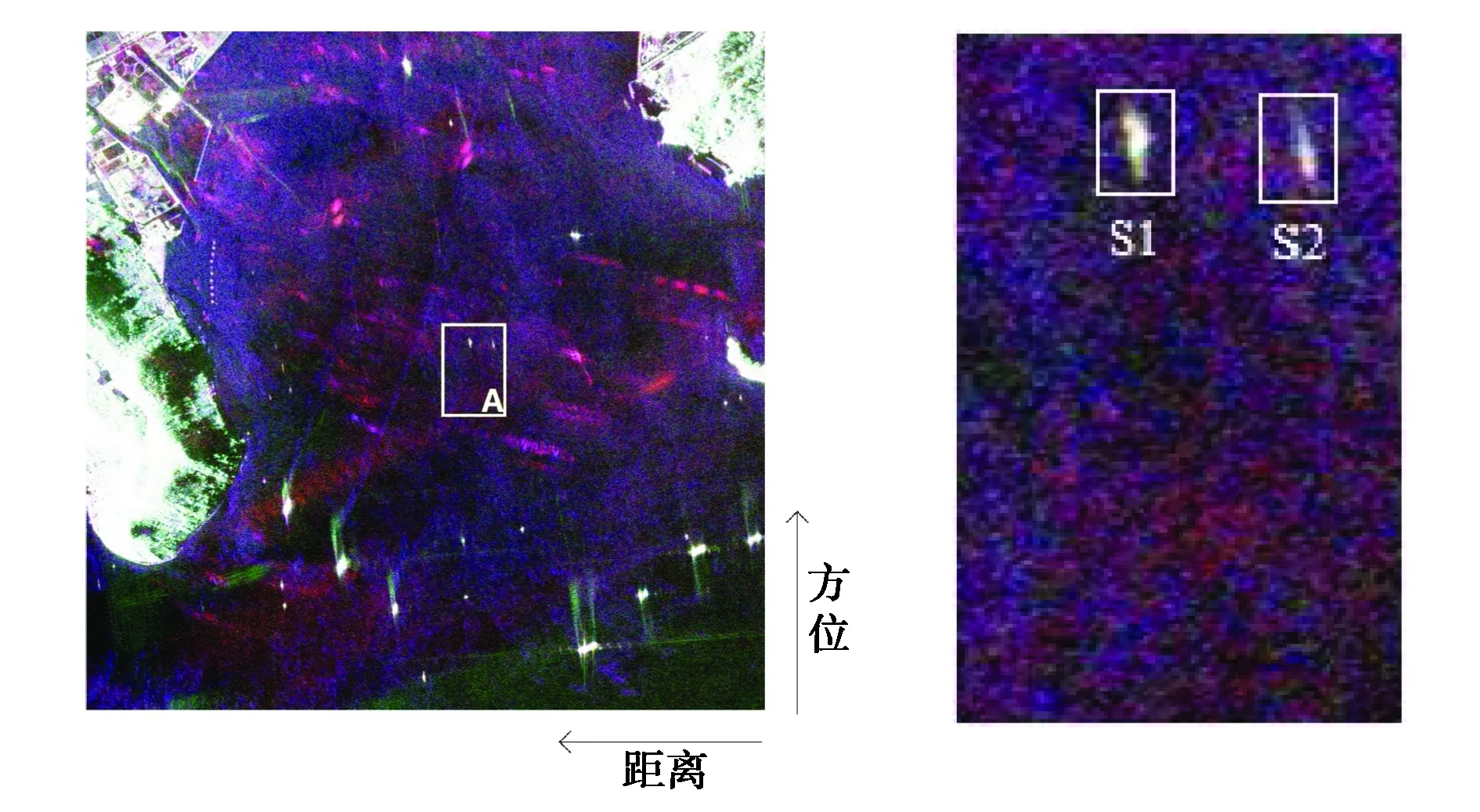
(a) CFAR检测区域 (b) 舰船目标图9 选取的极化SAR数据成像结果 (下载网址https://vertex.daac.asf.alaska.edu/)

采用文献[17]提出的方法进行模型辨识,得到图10所示结果,该图中k2、k3分别表示2阶、3阶对数累积量.从图10可以看出,区域A的分布接近Wishart分布结果,表明该区域杂波基本服从复Wishart分布,因而本文的推导结果对此适用．为了检测的需要,采用文献[18]提出的等效视数估计方法可得该区域等效视数为3.692 5,比较接近4视,也符合对多视检测性能验证的实验要求．

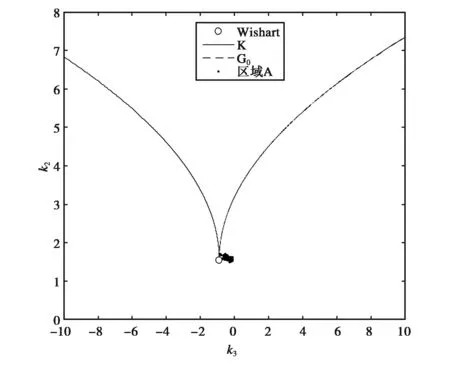
图10 区域A杂波模型辨识结果

4.1多视极化检测器性能比较

针对图9(b)对应的全极化SAR数据,采用文献[1]中协方差矩阵估计方法,估计出目标与杂波的协方差矩阵后,分别采用上述7种极化检测器计算出检测量,结果如图11所示．

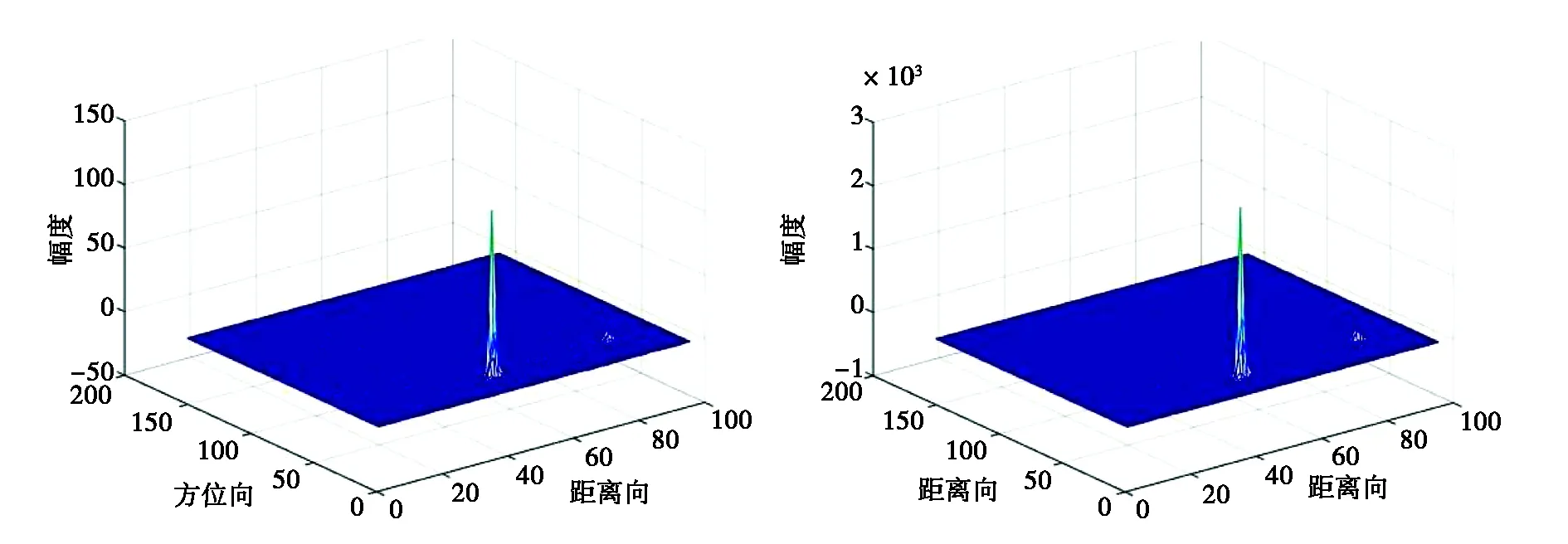
(a) OPD (TCR:35.709 4 dB) (b) ILRT (TCR:29.813 4 dB)

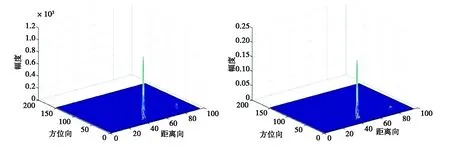
(c) PWF (TCR:28.897 3 dB) (d) PMF (TCR:28.865 1 dB)

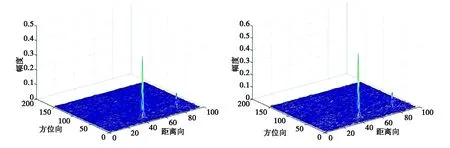
(e) OSD (TCR:20.540 3 dB) (f) SD (TCR:20.133 2 dB)

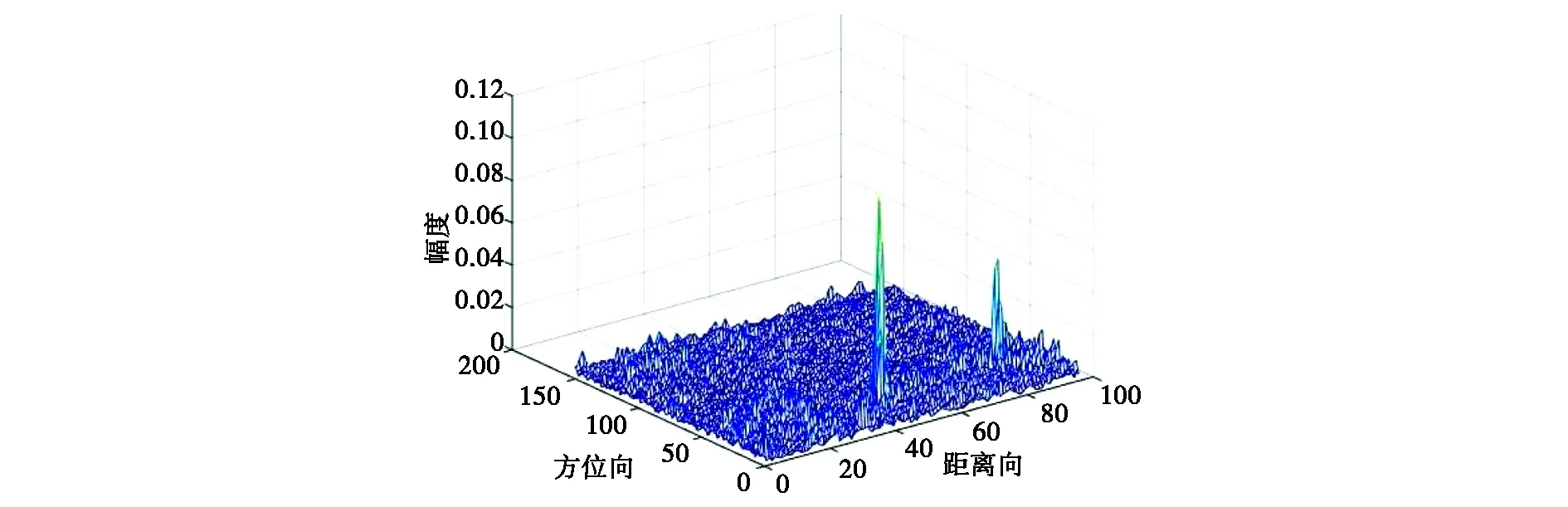
(g) SCD (VV极化, TCR:14.640 4 dB)图11 选取的极化SAR数据成像结果

由于区域A仅有14 688组像素数据,故设置虚警率为0.001,对图11所示的检测量计算结果进行二值化检测,可得图12所示的检测结果．

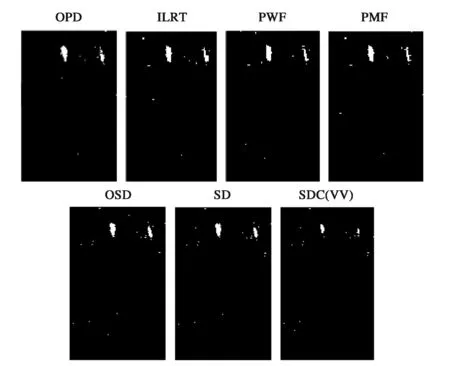
图12 不同检测器得到的二值检测结果

进一步,可得表5所示的检测性能对比结果,根据TCR的计算结果可以得到针对实测数据的检测性能排序为:OPD>ILRT>PWF>PMF> OSD≈SD> SCD．这与前文仿真得到的结果比较贴近,不同之处在于PWF与OSD检测性能略微下降．导致这一现象原因主要有二,其一是这一区域杂波统计特性不完全服从复Wishart分布;其二是对杂波协方差矩阵估计时存在误差．

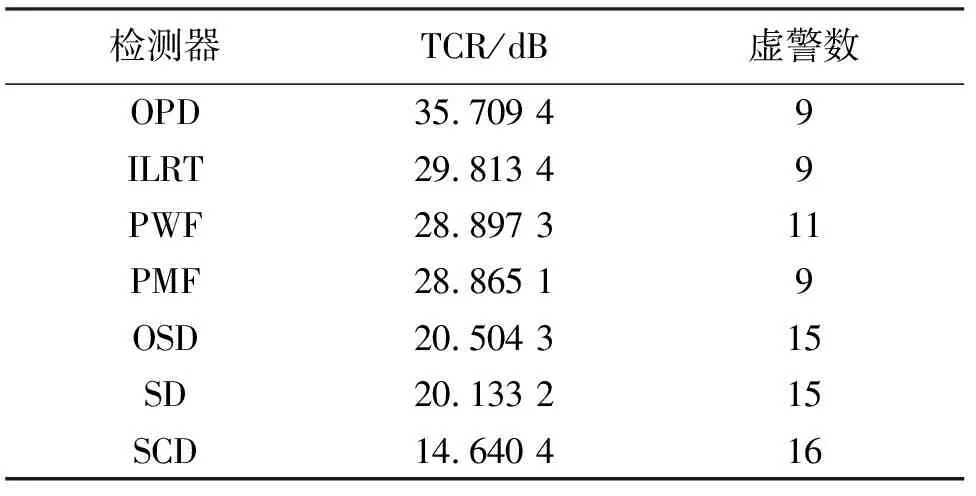
表5 不同检测器针对实测数据的检测性能对比

尽管OPD、ILRT、PMF这三种利用了目标协方差矩阵的检测器能够得到较优的检测性能,但其极易受协方差矩阵的估计精度影响,稍微改变目标协方差矩阵的估计范围,就会导致这三者的检测性能急剧减小,但SD、SCD检测器却不受协方差矩阵估计误差丝毫影响．

4.2理论门限CFAR检测效果分析

针对图11(f) 所示SD检测量的计算结果进行CFAR检测．虚警概率仍然设置为0.001,首先采用图像幅度值排序方法得到CFAR检测的标准门限,然后再用式(33)自适应地计算理论CFAR门限．这里,理论计算时多视视数取值采用估计得到的等效视数3.692 5,最后计算得到标准门限大小为0.017 95,而理论门限的计算结果为0.018 27,与实际结果较为接近．

同时采用两种门限对区域A进行目标检测得到图13所示的二值结果,检测效果相当,这也验证了理论推导结果的有效性．

(a) 标准门限 (b)理论门限图13 理论门限与标准门限检测效果对比

5 结 论

本文在将ILRT、OSD以及SCD检验统计量扩展至多视情形的基础上,推导了多视SD解析检测性能的两种数学形式,即公式(31)、(32),指出所有进行常系数加权的检测器都适用于该公式;分别采用蒙特卡洛仿真和解析方法获取7种多视极化检测器的检测性能;提出了公式(33)所示的一种基于Gamma函数的CFAR门限计算方法,从而适用于多视处理视数为非整数的情形;实测数据处理结果表明,检测性能对比分析结果与门限计算方法可靠有效．

[1] 王娜. 极化SAR图像人造目标检测技术研究[D]. 长沙:国防科技大学, 2012.

WANG N.Research on artificial target detection in polarimetric SAR images[D].Changsha: National University of Defense Technology,2012. (in Chinese)

[2] NOVAK L M, SECHTIN M B, CARDULLO M J. Studies of target detection algorithms that use polarimetric radar data[J]. IEEE transactions on aerospace and electronic systems,1989, 25(2):150-165.

[3] MARINO A. 基于几何扰动滤波的极化合成孔径雷达目标检测方法[M].万群, 译. 北京:国防工业出版社, 2014.

[4] NOVAK L M, BURL M C, IRVING W W. Optimal polarimetric processing for enhanced target detection [J].IEEE transactions on aerospace and electronic systems, 1993, 29(1): 234-244.

[5] CHANEY R D, BURL M C, NOVAK L M. On the performance of polarimetric target detection algorithms [J]. IEEE transactions on aerospace and electronic systems, 1993, 29(1): 234-244.

[6] VAN ZYL J, KIM Y J. Synthetic aperture radar polarimetry [M]. Hoboken: John Wiley & Sons, 2011.

[7] 刘国庆, 黄顺吉, TORRE A, 等. 一种新的多视全极化SAR目标检测器及其性能分析[J]. 信号处理, 1998(2): 110-116.

LIU G Q, HUANG S J, TORRE A, et al. A new multi detector full Pol-SAR target detector and its performance analysis[J]. Signal processing, 1998(2): 110-116. (in Chinese)

[8] 匡纲要, 陈强, 蒋咏梅,等. 极化合成孔径雷达基础理论及其应用 [M]. 长沙: 国防科技大学出版社, 2011.

[9] 张贤达. 矩阵分析引论[M]. 北京:清华大学出版社, 2004.

[10] 肖顺平, 杨勇, 冯德军, 等. 雷达极化检测器性能对比分析[J]. 宇航学报, 2014, 35(10): 1198-1204.

XIAO S P, YANG Y, FENG D J, et al. Contrastive analysis of the performances of radar polarimetric detectors[J]. Journal of astronautics, 2014, 35(10): 1198-1204.(in Chinese)

[11] 肖可可. 极化SAR图像相干斑抑制研究[D].长沙: 中南大学, 2012.

XIAO K K. Speckle reduction in polarimetric SAR images[D].Changsha:Central South University,2012.

[12] 刘国庆,黄顺吉,熊红,等.多视全极化合成孔径雷达图像的统计分析[J].电子科学学刊,1998,20(1):62-67.

LIU G Q, HUANG S J, XIONG H,et al. Analysis of multi look polarimetric synthetic aperture radar image statistics[J]. Journal of electronics, 1998,20(1):62-67. (in Chinese)

[13] 罗鹏飞. 随机信号分析与处理[M]. 北京:清华大学出版社, 2012.

[14] 代大海.POLSAR图像模拟及目标检测与分类方法研究 [D].长沙:国防科学技术大学,2003.

DAI D H. Research on POLSAR image simulation, target detection and classification[D]. Changsha: National University of Defense Technology, 2012.

[15] HANLEY J A, MCNEI B J. The meaning and use of the area under a receiver operating characteristic curve[J]. Radiology,1982,143: 29-36.

[16] GRADSHTEYN I S, RYZHIK I M. Table of integrals, series, and products[M]. San Diego: CA Academic Press, 2007: 106.

[17] 崔浩贵, 刘涛, 单洪昌, 等. 一种PolSAR图像统计模型辨识新方法[J]. 西安电子科技大学学报, 2015, 42(2): 199-205.

CUI H G, LIU T, SHAN H C. A new method for PolSAR image statistical model identification[J]. Journal of Xidian University, 2015, 42(2): 199-205. (in Chinese)

[18] LIU T, CUI H G, XI Z M, et al. Novel estimators of equivalent number of looks in polarimetric SAR imagery based on sub-matrices[J]. Science China information sciences, 2016, 59(6): 1-13.

张鹏(1996—),男,安徽人,研究方向为极化雷达目标检测算法、雷达极化统计理论以及地面动目标检测算法等理论工作．

张嘉峰(1993—),男,河北人,研究方向为极化雷达目标检测算法、雷达极化统计理论以及海上目标检测等工作．

刘涛(1978—),男,山东人,博士,现为海军工程大学教授,研究兴趣为雷达极化统计理论、极化信息处理、雷达极化检测与识别、电子战系统建模与仿真．已在IEEE Transactions,Science in China,China Physics B,中国科学,自然科学进展,物理学报,电子学报等期刊发表论文多篇．

Contrastiveanalysisoftheperformancesofradarmulti-lookpolarimetricdetectors

ZHANGPengZHANGJiafengLIUTao

(SchoolofElectronicEngineering,NavalUniversityofEngineering,Wuhan430000,China)

Contrastive analysis of the performances of radar polarimetric detectors can provide important reference for its design, while the detection performance evaluation theory is still imperfect, especially lacking of the analysis results for multi-look case. Based on the complex Wishart distribution of the polarimetric radar multi-look covariance matrix, a contrastive analysis of the performance of 7 classical polarimetric detectors is presented using both Monte Carlo simulations and analytical method after an area under curve (AUC) index is proposed for evaluation. The ranking result for 4-look case is: optimal polarimetric detector (OPD)> polarimetric whitening filter (PWF)≈identity likelihood ratio test (ILRT)> optimal sapn detector (OSD)> polarimetric matched filter (PMF)≈ span detector (SD)> single channel detector (SCD). At the same time, a novel approach to compute the constant false-alarm rate (CFAR) threshold is proposed based on Gamma function, and two kinds of general mathematical expressions of the theoretical performances of those detectors with linearly weighted form are also derived for multi-look case. Finally, the polarimetric SAR data is used to verify the above results.

radar polarimetry; multi-look processing; detection performance; CFAR threshold

张鹏, 张嘉峰, 刘涛. 雷达多视极化检测器性能对比分析[J]. 电波科学学报,2017,32(4):416-426.

10.13443/j.cjors.2017022401

ZHANG P, ZHANG J F, LIU T. Contrastive analysis of the performances of radar multi-look polarimetric detectors[J]. Chinese journal of radio science,2017,32(4):416-426. (in Chinese). DOI: 10.13443/j.cjors.2017022401

TN95

A

1005-0388(2017)04-0416-11

DOI10.13443/j.cjors.2017022401

2017-02-24

国家自然科学基金(基于对数空间理论的极化SAR图像舰船目标检测新方法61372165，基于协方差矩阵的极化干涉SAR图像海面慢动目标检测新方法研究61771483)

联系人： 刘涛 E-mail: liutao1018@sina.com