导出跃迁矩阵元计算公式的一个新方法

于熙龄

(辽宁大学 物理学院,辽宁 沈阳 110036)

导出跃迁矩阵元计算公式的一个新方法

于熙龄

(辽宁大学 物理学院,辽宁 沈阳 110036)

从量子场论的量子化思想和基本的理论结果出发,导出一个改进的跃迁矩阵元的计算公式,使它更加符合跃迁这一物理过程发生、发展的机理,可以在更广泛的范围内应用.

量子场;跃迁因子;跃迁矩阵元

0 引言

计算跃迁矩阵元是把量子场的基本理论应用于解决许多实际问题的重要途径.但是我们发现在现有的有关文献中,在处理这个问题时没有把场的量子化思想和基本的理论结果贯彻其中,反而把物理量和量子态都看作是时间的当然的连续函数,使得给出的跃迁矩阵元计算公式中有许多不尽人意之处.我们在此无意讨论这些问题,现在让我们从另一个思路出发,即从量子化思想和基本的理论结果出发,导出一个具有普遍意义的跃迁矩阵元的计算公式,使它更加符合跃迁这一物理过程发生、发展的机理.

1 哈密顿算符及其作用时间

在相互作用表象中,量子系统的相互作用哈密顿算符与时间有关,这一点也体现在各量子场平面波展开式中的湮灭算符和产生算符身上,它们起作用的时间是与包含它们的场量展开式中的时间t绑定的.它们在起作用的时间点上将湮灭和(或)产生一些粒子,使量子态发生不连续的突变.我们曾在本文参考文献[1]的(12)式中把来自场量展开式的湮灭算符和产生算符起作用的时间用下角标来表示.现在,我们将下角标移到表达式内,把湮灭算符和产生算符改写成如下形式

(1)

(2)

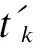
(3)

任意两个相邻的时间节点之间的差可记为

(4)

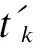
(5)

在其它时间节点处有类似情况.电磁相互作用哈密顿算符HI与此类似.

2 量子态的演化和跃迁矩阵元

(6)

在以下的推导中,为书写简单,暂时将变量tk的下角标去掉,在最后的结果中再恢复.为贯彻场量的量子化思想及其基本的理论结果,我们将上式离散化,改写成差分形式,有

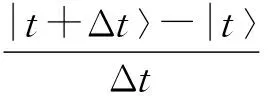
|t+Δt〉-|t〉=-iHI(t)|t〉Δt

上式的右边部分可改写成积分形式,有

或

恢复下角标,有

=[1+W(k+1,k)]|k〉

(7)

(7)式给出了相邻的两个量子态之间的递推关系.式中

(8)

当m=1时,已如(7)式所示.

当m=2时,有

|k+2〉=[1+W(k+2,k+1)]|k+1〉

(9)

把(7)式代入(9)式,有

|k+2〉=[1+W(k+2,k+1)][1+W(k+1,k)]|k〉

(10)

当m=3时,同理有

|k+3〉=[1+W(k+3,k+2)][1+W(k+2,k+1)][1+W(k+1,k)]|k〉

…………,

原则上,k可从任意值起,k=(1,2,3,…),递推到任意的第(k+m)态:

|k+m〉=[1+W(k+m,k+m-1)]……[1+W(k+2,k+1)][1+W(k+1,k]|k〉

(11)

(11)式是利用递推的方法得到的量子态演化方程的一般解.现在如果我们把k=1的态|1〉作为量子反应过程开始的初态,(11)式可简单地写成

|m+1〉=[1+W(m+1,m)]……[1+W(3,2)][1+W(2,1)]|1〉

(12)

考虑到由(12)式给出的量子态的跃变只是粒子的种类和数量的改变,不涉及其它的物理条件,得到的|m+1〉态是个通解,是各个可能的特解的线性叠加.如果我们假定第1态是个物理条件确定的初态,记为|1〉i,而需要求解的是一个符合题设物理条件的特解.这时可用量子态的完备性条件

(13)

把(12)式表示成各个特解的线性叠加,

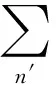
(14)

再从中把感兴趣的那一个特解,例如(14)式中下角标为某个f的那一个,抽取出来,就有

(15)

用符号Sf,i表示此式中的矩阵元,有

(16)

它就是从确定的态|1〉i经过m步到达我们感兴趣的态|m+1〉f的跃迁矩阵元(或跃迁振幅).

3 跃迁矩阵元的简化

将(16)式中的连乘积展开,会得到一个很复杂多项式,但是在此多项式中不是每一项都对跃迁矩阵元有贡献,有的项能够使量子反应过程从初态到达末态,称这样的项为有效项;相反,有的项对跃迁矩阵元没有贡献,称为无效项,因此可将它们事先剔除.为剔除那些无效项,既简单又明确的办法是在(16)式中相乘的各因子之间插入类似于(13)式的完备性条件,求出每一步跃迁的矩阵元.例如当m=2时,可将(16)式写成

Sf,i=f〈3|[1+W(3,2][1+W(2,1]|1〉i

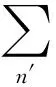
={f〈3|[1 +W(3,2]|2〉f1}{f1〈2|[1+W(2,1]|1〉i}

={f〈3|[W(3,2]2〉f1}{f1〈2|[W(2,1]|1〉i}

=Sf,f1Sf1,i

(17)

即从确定的第1态|1〉i到确定的第3态|3〉f的跃迁矩阵元等于从第1态到第2态的跃迁矩阵元和从第2态到第3态的跃迁矩阵元的乘积,而且对每一步的跃迁矩阵元有贡献的仅仅是由(8)式给出的跃迁因子W(k+1,k),而与跃迁因子相加的数字1没有贡献.显然,这种做法可用于其它类似的地方,这样(16)式可改写成

Sf,i=Sf,fmSfm,m-1,……Sf2,f1Sf1,,i

(18)

此式就是我们给出的计算跃迁矩阵元的公式.其中的任何一步都可利用(8)式算出.为使(8)式中的积分呈四维的时空形式,我们可将哈密顿算符写成哈密顿密度算符的体积分.例如,在电磁相互作用下,利用(5)式,可写成

(19)

上述的(16)式是态的运动方程(6)在离散的情况下,通过递推关系得到的,其间没做任何其他近似,得到的解(11)或(12)是态方程的严格解,因而这个解中的跃迁矩阵元(18)式也就当然是这个过程中跃迁机理的严格表述.

为描述一个完整的量子反应过程,需要多少个时间节点呢？是需要无穷多个才‘精确’吗？不是的！现在我们感兴趣的绝大多数问题都是只要几个节点就够了.这是因为哈密顿算符中包含的湮灭算符和产生算符的总数有限,在每个节点处,哈密顿算符的不同仅在于湮灭算符和产生算符各自的数目不同,它们的总数是固定的.因此它们的不同的编排方式也是有限的,每种编排方式都会很快地重复出现.一个量子过程从初态开始,一经达到终态,过程就停止了,完成了.这期间需要多少个节点,可根据哈密顿算符的结构和已有的物理知识作出判断.例如,由(5)式给出的哈密顿密度算符,其中包含三个场量,每个场量中有一个湮灭算符和一个产生算符,总共六个.如果问题不涉及正电子,将正电子的湮灭算符和产生算符排除,就只剩下光子的湮灭算符(a)和产生算符(a+),电子的湮灭算符(c)和电子的产生算符(c+),这四个算符了.由(5)式可知,把这四个算符分成每三个一组的正规乘积组合,每组内必须有一个电子的湮灭算符,一个电子的产生算符和一个光子算符(湮灭算符或产生算符),这就只有两种组合了:(c+ca)和(c+a+c).对于我们感兴趣的量子反应过程,通常是始末状态的粒子都是那些处于自由状态时是稳定的粒子.如果过程是从(c+ca)开始到(c+a+c)结束,则符合要求的粒子反应只需两个节点的跃迁就可以精确描述了.这时由(4)式表达的两节点之间的宽度只有一个,因此,这个时间宽度既是涨落子q的寿命也是这个反应过程的特征时间了.这其中的详细情况可参阅本文参考文献[1].

4 结语

综上所述,由于(18)式给出的跃迁矩阵元表达式是个精确解,它清楚地反映了跃迁过程的步骤和机理.它不是按某个小量的展开,即它不是‘微扰’展开,因而不属于‘微扰论’的范畴.对任何一个粒子反应过程,只要确定了节点的个数,不论是强相互作用还是弱相互作用,不论给出的结果在数值上有多么大或多么小,都是有限的精确结果！

[1] 于熙龄.对传播函数的一个质疑和量子场的涨落[J].辽宁大学学报：自然科学版,2017(1)：18-24.

[2] 朱洪元.量子场论[M].北京：科学出版社,1960.

[3] 辛忠政,宫学惠.量子场论简明教程[M].沈阳：辽宁大学出版社,1992.

[4] 殷鹏程.量子场论纲要[M].上海：上海科学技术出版社,1986.

[5] 程国均,杨守智.量子场论引论[M].成都：四川大学出版社,1980.

[6] 何宝鹏,熊钰庆.量子场论导论[M].广州：华南理工大学出版社,1990.

[7] Bjorken J D,Drell S D.Relativistic Quantum Fields.McGraw-Hill Book-Company,1965.(中译本:相对论量子场,科学出版社,1984).

[8] 陈亚孚.量子电动力学导论——光子学导引[M].北京：兵器工业出版社,1992.

[9] Itzykson C,Zuber J B.Quantum Field Theory[M].McGraw-Hill Inc,1980.

(责任编辑郑绥乾)

更正声明

辽宁大学学报(自然科学版)2017第1期《对传播函数的一个质疑和量子场的涨落》中的(14)(17)(24)(25)式书写有误,它们分别应为:

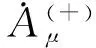
(14)

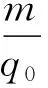
(17)

(24)

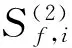
(25)

特此更正.

ANewMethodforDerivingtheFormulaofTransitionMatrixElement

YU Xi-ling

(CollegeofPhysics,LiaoningUniversity,Shenyang110036,China)

The paper is based on quantization of quantum field theory and basic theoretical results,an improved formula for calculating the transition matrix element is derived,which to be make more in line with the mechanism of the occurrence and development of the physical process of transition,which can be used in a wider range of applications.

quantum field;transition factor；transition matrix element

2017-05-14

于熙龄(1937-)，男，沈阳人，满族，教授，从事理论物理研究.

O 413.2

A

1000-5846(2017)03-0229-05