一类不连续动力系统的滑模运动

唐晓伟

(齐鲁师范学院 数学学院,山东 济南 250200)

一类不连续动力系统的滑模运动

唐晓伟

(齐鲁师范学院 数学学院,山东 济南 250200)

利用不连续动力系统的流转换理论研究了一类不确定项和控制输入在同一点写入状态方程的二阶不连续动力系统的滑模运动,给出了分离边界上可穿越流和滑模运动出现的解析条件.最后用单摆模型进行仿真,验证了结论的有效性.

不连续动力系统;滑模运动;可穿越流

0 引言

不确定项与控制输入在同一点写入状态方程的控制问题,即匹配条件下的鲁棒问题是非线性反馈控制系统中的一类重要问题[1-4].利用李雅普诺夫函数来设计控制律时,李雅普诺夫函数的选择是其中的难点,因为系统的流在到达流形时的状态是未知的,我们只能通过系统的特点结合经验来给出备选李雅普诺夫函数,这使其在实际应用过程中受到限制[5].Luo[6-7]在研究不连续动力系统的复杂动力学行为时提出了流转换理论.该理论可简洁地描述子系统的流在到达分离边界时的状态,从而能更清晰地描述系统的复杂动力学行为.鉴于此,本文我们将利用不连续动力系统的流转换理论来研究一类不连续动力系统的滑模运动,为非线性反馈控制提供必要的理论前提.

1 预备知识

考虑不确定项和控制输入在同一点写入状态方程的二阶系统

(1)

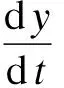
流形S将整个平面R2分为Ω1和Ω2两部分,其中

Ω1={(x,y)|ax+y>0)},Ω2={(x,y)|ax+y<0)}.

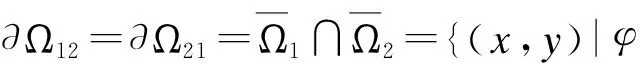
将系统(1)和分离边界∂Ω12看作是一个不连续动力系统,将其描述为

(2)

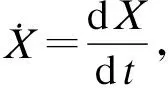
F(0)(t,X)=(y,-ay)T,X∈S;

F(1)(t,X)=(y,h(X)+g(X)u)T,X∈Ω1;

F(2)(t,X)=(y,h(X)+g(X)u)T,X∈Ω2.

2 解析条件

对不连续动力系统(2),给出如下假设:

(H1):相邻子系统之间的流的转换具有时间上的连续性;

(H2):对于一个无界的子区域Ωi,必存在一个开域Di⊂Ωi,使得在Di内相应的向量场和流是有界的;

(H3):对于一个有界的子区域Ωi,必存在一个开域Di⊂Ωi,使得在Di内相应的向量场是有界的,但是流可以是无界的.

定义1对不连续动力系统(2),假设在时刻tm,区域Ωi内的流到达分离边界∂Ω12,对∀ε>0,定义区域Ωi,i=1,2内的流在分离边界∂Ω12法方向上的零阶G函数分别为

(3)

注:式(3)可写为

(4)

事实上,将X(1)(tm-ε)在X(1)(tm-)处展开成泰勒级数,有

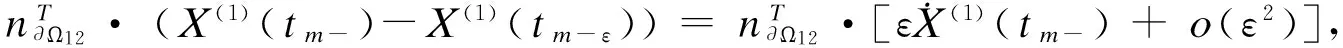
同样的,有

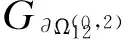
定理1分离边界∂Ω12上可穿越流[6]产生的充要条件为

(5)

其中Xm=(x(0)(tm),y(0)(tm))T=(x(tm),y(tm))T,tm为区域Ωi,i=1,2内的流到达分离边界∂Ω12的时刻.

证明由不连续动力系统的流转换理论可知,分离边界∂Ω12上可穿越流产生的充要条件为

(6)

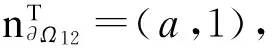
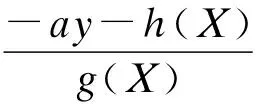
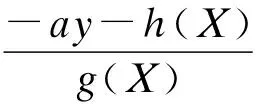
定理2若对任意的X∈R2,控制输入u满足

(7)

则分离边界∂Ω12上会出现滑模运动[6].

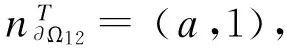
(8)

若(7)式成立,(8)式显然成立,即分离边界∂Ω12上会出现滑模运动.

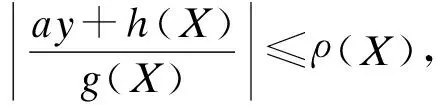
(9)

其中k>0为常数,则分离边界∂Ω12上会出现滑模运动.

证明:由(9)式可得,

从而(7)式成立,即分离边界∂Ω12上会出现滑模运动.

定理3分离边界∂Ω12上滑模运动消失的充要条件为

(10)

其中tm为滑模运动消失的时刻.

证明:由流转换理论知,分离边界∂Ω12上滑模运动消失的充要条件为

(11)

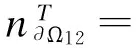
3 数值模拟与仿真

考虑如下的单摆系统

(12)

其中m表示单摆的质量,l,k0和g0分别为摆线的长度,摩擦系数和重力加速度.取流形S为x+y=0,当|x|≤π,|y|≤π时,系统(12)与流形S所组成的不连续动力系统满足假设(H1)—(H3).此时,Ω1={(x,y)|x+y>0},Ω2={(x,y)|x+y<0},∂Ω12={(x,y)|x+y=0}.

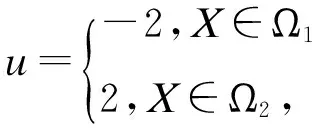
[1] 俞立.鲁棒控制[M].北京:清华大学出版社,2002.

[2] 孔屹刚,王志新.大型风电机组模糊滑模鲁棒控制器设计与仿真[J].中国电机工程学报,2008,28(14):136-141.

[3] 李宁璨,徐政,唐庚,等.基于滑模鲁棒控制器的有功功率调制在多端直流输电的应用[J].中国电机工程学报,2016(3):664-673.

[4] 张昌凡,王耀南.神经网络滑模鲁棒控制器及其应用[J].信息与控制,2001,30(3):209-212.

[5] 马里诺.非线性系统设计[M].北京:电子工业出版社,2006.

[6] Luo A C.A theory for non-smooth dynamical systems on connectable domains [J].Communications in Nonlinear Science and Numerical Simulation,2005,10(1):1-55.

[7] Luo A C.Imaginary,sink and source flows in the vicinity of the separatrix of non-smooth dynamic systems [J].Journal of Sound and Vibration,2005,285(1/2):443-456.

(责任编辑郑绥乾)

SlidingMotionforaDiscontinuousDynamicalSystem

TANG Xiao-wei

(MathematicalSchool,QiluNormalUniversity,Jinan250200,China)

The sliding motion for a second-order discontinuous dynamical system with uncertainties and control inputs at the same point is studied by using the flow transporting theory of the discontinuous dynamical systems.The analytical conditions for the passing flow and the sliding motion on the separation boundary are given.Finally,using a pendulum model,the effectiveness of conclusions is verified.

discontinuous dynamical system;sliding motion;passable flow

2017-03-10

国家自然科学基金(11571208);山东省高校科技计划项目(J16LI13)

唐晓伟(1983-),女,讲师, 硕士,主要从事不连续动力系统研究,E-mail:dangmy@163.com.

O 231.2

A

1000-5846(2017)03-0197-05