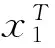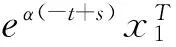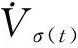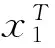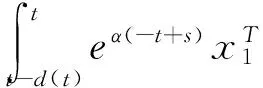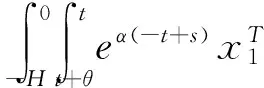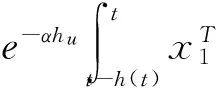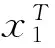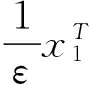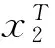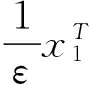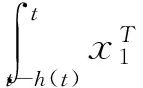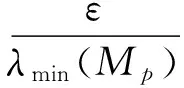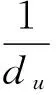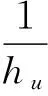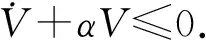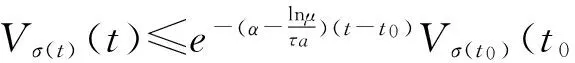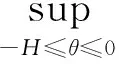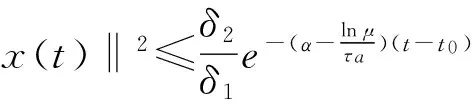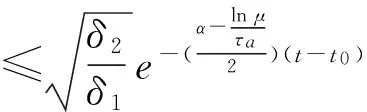混合时滞级联切换系统的指数稳定
2017-11-24段连伟赵胜芝
段连伟,赵胜芝
(辽宁大学 数学院,辽宁 沈阳 110036)
混合时滞级联切换系统的指数稳定
段连伟,赵胜芝*
(辽宁大学 数学院,辽宁 沈阳 110036)
切换系统是一类重要的混杂系统.在实践中有着广泛地应用.研究含有混合时滞的级联非线性切换系统的指数稳定问题.
级联系统;混合时滞;指数稳定
1 问题陈述
考虑如下非线性级联切换系统
(1)
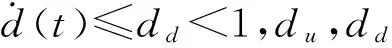
定义1如果切换系统(1)满足
‖x(t)‖≤α1‖x(t0)‖ce-β1(t-t0),∀t≥t0,
(2)

定义2对任意的时间T2>T1≥0和给定的切换信号σ(t),如果存在τa>0和N0≥0,满足
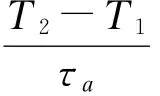
(3)
其中Nσ(T1,T2)表示在[T1,T2)内的切换次数,则称τa为平均驻留时间,N0叫做振荡界.不失一般性,取N0=0.
假设1存在常数η≥0,满足
0 (4) 假设2假设存在Z>0光滑正定函数Wp(x2(t)),存在bp>0,q1>0,q2>0(p∈S),满足 (5) q1‖x2‖2≤Wp(x2)≤q2‖x2‖2. (6) 引理1对于∀x,y∈Rr,∀ε>0,存在正定对称矩阵Π,满足不等式 (7) 引理2对于任意适当维数的矩阵Z>0及标量τ2>τ1>0,下列不等式成立 (8) 其中τ12=τ2-τ1. 对于切换系统(1),有以下指数稳定结果. 定理1如果存在ε>0,μ≥1和正定对称矩阵Pi,Qi,Zi,Yi,Hi,Mi,Ei,Ti,满足 (9) Pi≤μPj,Qi≤μQj,Zi≤μZj,Yi≤μYj,∀i,j∈S,i≠j, (10) 且平均驻留时间τa满足 (11) 则混合时滞级联切换系统(1)指数稳定. 证明选取如下Lyapunov-Krasovskii函数 (12) 沿着系统(1)的轨迹,可得 由引理2,可得 由引理1,可得 (13) (14) (15) 由(13)-(15),可得 其中 (16) (17) (18) (19) 从而有 (20) 由(10)和(12),可得 Vi≤μVj,∀i,j∈S,i≠j. (21) 因此当t∈[tk,tk+1)时,有Vσ(t)(t)≤e-α(t-tk)Vσ(tk)(tk). 由(12)和假设2,可得 Vσ(t)(t)≥d1‖x1(t)‖2+q1‖x2(t)‖2, 其中d1=min{λmin(Pi),i∈S}. (22) 其中 d2=max{λmax(Pi),i∈S}+H·max{λmax(Qi)+λmax(Zi)H+λmax(Yi)hu,i∈S}, δ1=min{d1,q1},δ2=max{d2,q2}. 进而有 (23) 其中x(t)=(x1,x2)T.从而有 所以 ‖x(t)‖≤α1‖x(t0)‖ce-β1(t-t0). (24) 因此时滞级联切换系统(1)指数稳定. [1] Li S,Xiang Z R,Karimi H R.Stability andL1-gain controller design for positive switched systems with mixed time-varying delays[J].Applied Mathematics and Computation,2013(222):507-518. [2] Zhai J Y,Wang B,Fei S M.Tracking control for switched nonlinear systems with muitiple time-varying delays[J].Nonlinear Analysis:Hybrid Systems,2015(17):44-55. [3] Jin Y,Fu J,Zhang Y M,Jing Y W.Reliable stabilization of switched system with average dwell-time approach[J].Journal of the Franklin Institute,2013(350):452-463. (责任编辑郑绥乾) ExponentialStabilityofCascadeSwitchedSystemswithMixedDelays DUAN Lian-wei,ZHAO Sheng-zhi* (SchoolofMathematics,LiaoningUniversity,Shenyang110036,China) Switched systems are a class of hybrid systems.It has been widely used in practice.This paper studies the exponential stability problem for cascade switched systems with mixed delays. cascade systems;mixed delays;exponential stability 2016-11-14 段连伟(1986-),男,山东潍坊人,硕士研究生,研究方向:非线性级联切换系统. * 赵胜芝(1965-),女,辽宁铁岭人,教授,研究方向:非线性切换系统. O 231 A 1000-5846(2017)03-0193-04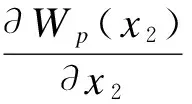
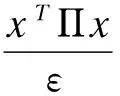
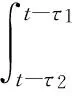
2 主要结果