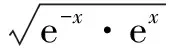函数极值点偏移的判定和应用
2017-11-23尹爱国
尹爱国
(湖南省长沙市明德中学,湖南 长沙 410000)
函数极值点偏移的判定和应用
尹爱国
(湖南省长沙市明德中学,湖南 长沙 410000)
综述函数的极值条件,结合极值点偏移的性质,提出极值点偏移的判定方法.
函数极值点;判定方法;应用
问题引入:(2016·全国卷Ⅰ·理21)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.
(Ⅰ)求实数a范围;
(Ⅱ)设x1、x2是f(x)的两个零点,证明:x1+x2<2
解析(Ⅰ)答案:a>0.

笔者在多年的教学中发现类似问题在高考压轴题中频频出现,因此对此类问题进行了研究,找出了解决此类问题的一种通法,供大家参考.
一、极值点偏移的判定方法.
设已知函数y=f(x),在区间x∈D上满足:x=a是函数的唯一极值点,x1,x2∈D,x1≠x2,f(x1)=f(x2)
第一步:判断曲线在D上的开口方向.
类似于抛物线,若曲线f(x)在D上存在唯一极值点,则曲线在D上存在开口方向问题.若x=a为y=f(x)的极小值点,则f(x)在D上的开口向上;若x=a是曲线y=f(x)的极大值点,则y=f(x)在D上的开口向下.
第二步:构造函数F(x)=f(x)-f(2a-x)或F(x)=f(a-x)-f(a+x).运用导数判定x 下面结合上述步骤解决文首提出问题的第二问. (Ⅱ)解由(Ⅰ)有:a>0,x=1为y=f(x)的唯一极值点,且为极小值点,函数定义域为R,∴f(x)的图象在R上开口向上.构造函数F(x)=f(x)-f(2-x)=xe2-x+(x-2)ex. 求得F′(x)=(x-1)(ex-e2-x).x=1时,F′(x)=0,x≠1时,F′(x)>0,∴F(x)R上递增. 又F(1)=0,∴x<1时,F(x) 例(2014·江苏南通二模·20题)设函数f(x)=ex-ax+a(a∈R),其图象与x轴交于点A(x1,0),B(x2,0)(x1 (Ⅰ)求a的取值范围; 解析(Ⅰ)定义域为x∈R,f′(x)=ex-a. 当a≤0时,f′(x)>0,f(x)在R上递增,函数不可能有两个极值点.当a>0时,∵当x∈(-∞,lna)时,f′(x)<0,x∈(lna,+∞)时,f′(x)>0. ∴f(x)在(-∞,lna)上单调递减,在(lna,+∞)上单调递增. ∴当x=lna时,f(x)min=f(lna)=elna-alna+a=2a-alna. ∵f(x)的图象与x轴有两交点, ∴f(x)min=2a-alna<0, ∴a>e2. (Ⅱ)证明:由(Ⅰ)知:a>e2,x=lna为y=f(x)的唯一极值点,且为极小值点. ∴f(x)的图象开口向上. ∴x1 ∴F(x)在(0,+∞)上单调递减,∴F(x) [1]华东师范大学数学系.数学分析[M].北京:高等教育出版社,1991. [2]谭琨.多元函数极值的研究与应用[J].安庆师范学院学报,2005. [责任编辑:杨惠民] 2017-07-01 尹爱国,男,中学一级教师,硕士,长沙市骨干教师,从事高中数学教学研究. G632 A 1008-0333(2017)28-0027-02


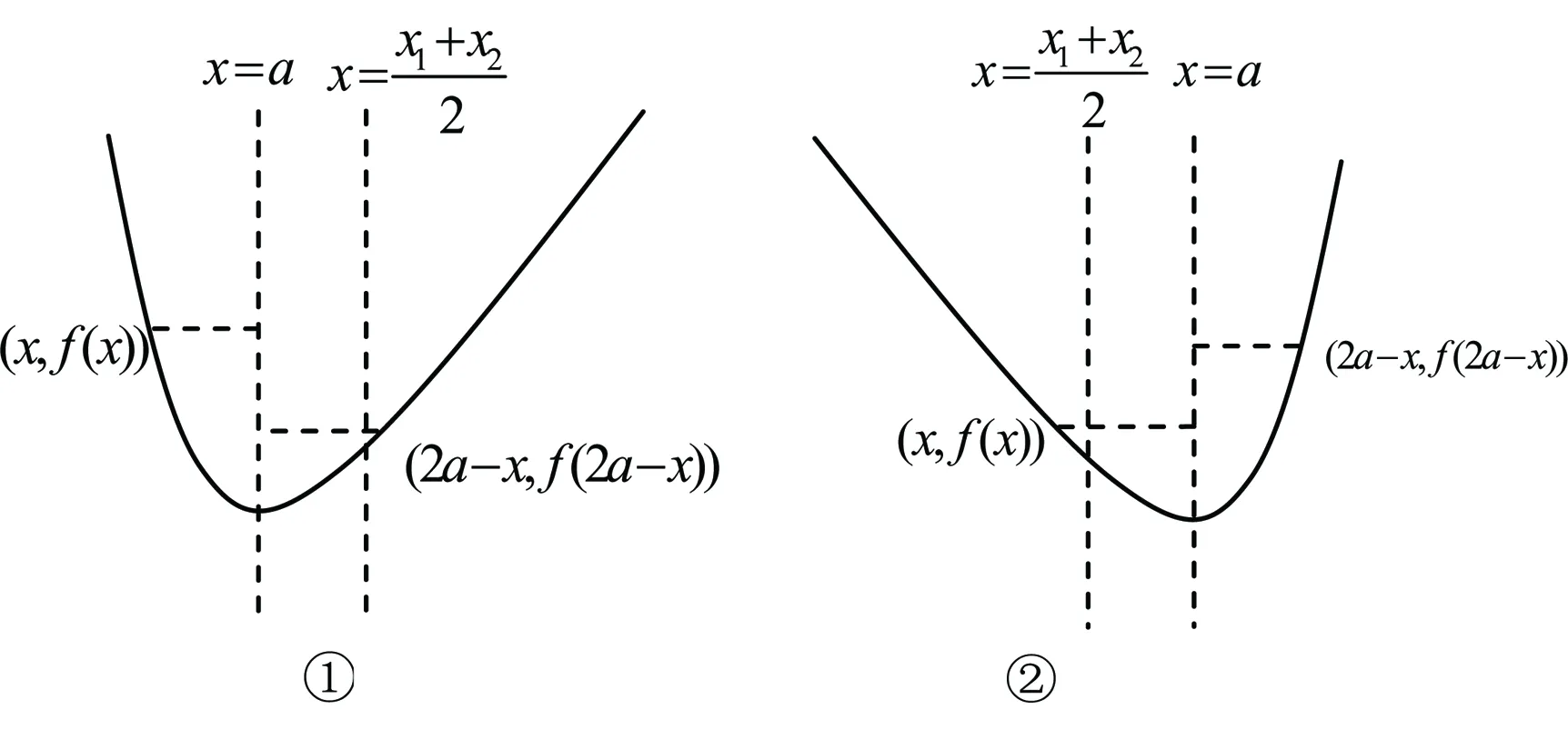



二、极值点偏移的性质



三、例题展示