“外接球”问题的解题策略

崔红光 杨苍洲

(1.福建省泉州实验中学，2.福建省泉州第五中学,福建 泉州 362000)

“外接球”问题的解题策略

崔红光1杨苍洲2

(1.福建省泉州实验中学，2.福建省泉州第五中学,福建 泉州 362000)

本文通过近年来部分高考试题中外接球的问题，利用化归思想，最终都转化为四个模型，通过对模型的求解来求几何体外接球的半径．

外接球；球心；构造；几何体

有关外接球的立体几何问题是近年高考试题的难点之一，这与学生的空间想象能力以及化归能力有关.《普通高中数学课程标准》中对立体几何初步的学习提出了基本要求：“在立体几何初步部分，学生将先从对空间几何体的整体观察入手，认识空间图形；再以长方体为载体，直观认识和理解空间点、线、面的位置关系；……”由此可见，长方体模型是学习立体几何的基础，掌握长方体模型，对于学生理解立体几何的有关问题起着非常重要的作用.

几何体的外接球问题实质是解决球的半径或确定球心O的位置问题，其中球心的确定是关键．而利用球心定义或球心与其截面的圆心连线垂直于截面这一性质，就是确定球心位置的理论依据.即球心可以通过作出过几何体某两个面的外接圆圆心，且垂直于相应面的垂线，则两直线交点即为球心.

我们可以将几何体的外接球问题分为以下几类题型.

一、柱体的外接球

1.圆柱的外接球球心为上下底面圆心连线中点；

2.直棱柱的外接球球心为上下底面外接圆的圆心连线中点；

特别的，长方体，正方体的外接球的球心是其体对角线中点.

二、椎体的外接球

1.正棱锥的外接球的球心在其高上，具体位置可通过计算找到．

2.构造长方体或正方体或直棱柱确定球心

(1) 有一组线面垂直的棱锥，以该线为侧棱，该面为底补成直棱柱；

(2) 构造长方体确定球心，构造策略：长方体的八个顶点可以构造出三棱锥或四棱锥.

① 有一个面是直角三角形或矩形，一条侧棱和该面垂直的三棱锥或四棱锥；

② 有共斜边的两个直角三角形的三棱锥，则公共斜边的中点就是其外接球的球心；

③ 对棱相等的三棱锥，特别的，正四面体可转化到正方体中；

④ 底面是矩形，一个侧面是直角三角形且垂直于底面， 这两个面的交线是三角形的斜边，满足上述条件的四棱锥.

3.过几何体的两个面的外接圆的圆心分别作两个面的垂线，垂线的交点为球心.

4.圆锥的外接球： 圆锥的轴截面的外接圆的圆心为球心 .

三、例题分析

例1 在三棱柱ABC-A1B1C1中，AA1⊥平面ABC，CA=AB=2，AA1=6，∠ACB=120°．若三棱柱ABC-A1B1C1的所有顶点都在球O的表面上，则球O的表面积为( )

A．20π B．42π C．52π D．56π

解设底面△ABC的外接圆半径为r，球O的半径为R,则

例2 (2014高考全国大纲卷)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( ).

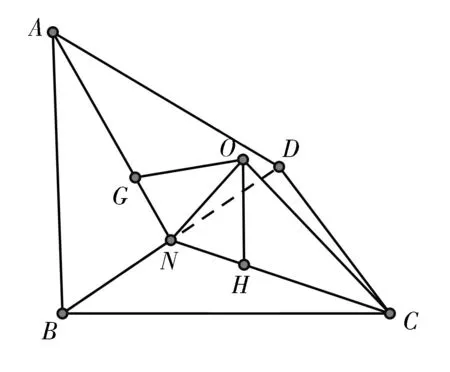
例5 在四面体ABCD中，AB=CD=2，AD=BC=3，AC=BD=4，求四面体ABCD外接球的表面积.

A．10π B．4π C．16π D．8π

A.25π B．26π C．27π D．28π

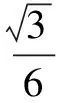
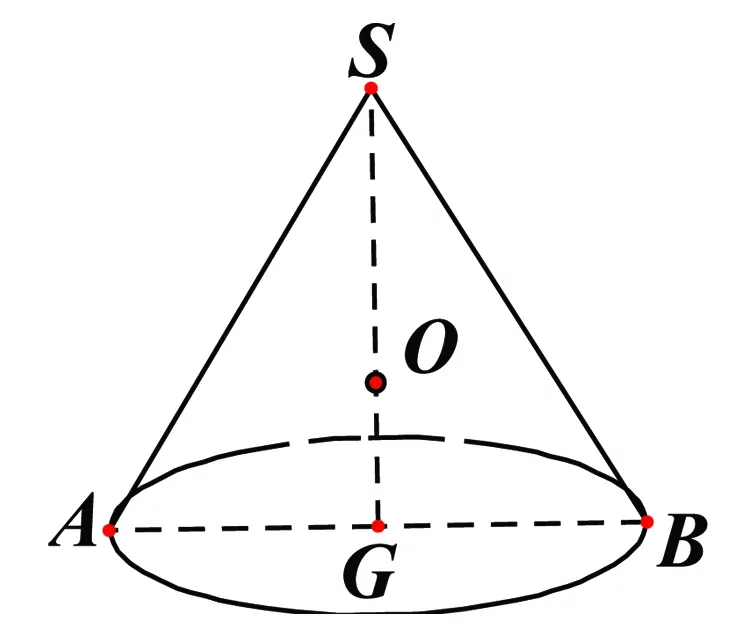
例8 已知一个几何体的正视图及侧视图均是边长为2的正三角形，俯视图是直径为2的圆，求该几何体的外接球的表面积.

[1]人民教育出版社 课程教材研究所 中学数学课程教材研究开发中心. 普通高中课程标准试验教科书( 必修)数学4(A版)[M]. 北京:人民教育出版社,2014.

[责任编辑：杨惠民]

2017-07-01

崔红光(1981-10)，女，黑龙江，任职于福建泉州实验中学，中学一级，大学本科，主要从事高中数学教学研究.

杨苍洲(1979,12)，男，福建惠安，福建省泉州第五中学，中学高级，大学本科，主要从事高中数学教学研究.

G632

A

1008-0333(2017)28-0007-02