导数，物理解题的一把利器

冯云周

(河北隆尧第一中学，河北 邢台 055350)

导数，物理解题的一把利器

冯云周

(河北隆尧第一中学，河北 邢台 055350)

运用数学知识处理物理问题是当今高考对学生的能力考查之一，而导数又是现行高中数学教材中的一项新增内容，因此，如何把导数知识很好地运用到高中物理解题的实际中去，已经成为了很多人正在积极探索和研究的一项新课题.本文在这方面做出了一些初步的尝试.

导数；高中物理；解题

现行的高中数学课本中新增了对导数等内容的学习，为中学生应用高等数学知识来解决问题奠定了知识基础.实际上，许多高中物理题如果用导数来分析和求解，就会显得思路简捷，便于理解和接受，解题效果也会不同凡响.下面是我在平时的教学实践中，尝试运用导数来解中学物理题的一些初步的探索和体验，现分享给大家，希望能给您带来一些启迪！

一、巧用导数，豁然开朗

题1 一物体沿x轴做简谐运动，振幅为8cm，频率为0.5Hz，在t=0时位移是4cm，且向x轴负方向运动，试写出用正弦函数表示的振动方程.

这是最近我的学生们所做的一道练习题，所附解答如下：

设简谐运动的表达式为：x=Asin(ωt+φ)

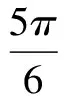
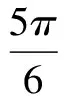
冥思苦想了一会儿，我忽然灵光一闪：“物体向x轴负方向运动”，说明此时速度为负，而位移对时间的一阶导数不正是速度吗！于是我得出了下面的解释：

如此稍加点拨，是否有豁然开朗的感觉呢？

二、耳目一新，教学相长

题2 如图1所示，为一单摆的共振曲线，该单摆的摆长约为多少？共振时单摆的振幅是多大？共振时摆球的最大速度和最大加速度各为多少？(g取10 m/s2)

图1

这是在学习共振时我给学生们讲解的一道例题，这道题的重点和难点在最后一问，一般解法如下：

从共振曲线可知，单摆发生共振时，振幅A=8cm.设单摆的最大偏角为θ，摆球所能达到的最大高度为h，由机械能守恒定律得：

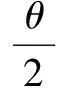
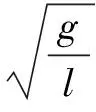
摆球在最大位移处加速度最大，有mgsinθ=mam

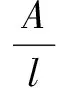
那么，这道题有没有其他更好的解法呢？当我在办公室里深入思考的时候，一向学习认真、善于思考的张同学轻声打报告走了进来，向我展示了他的做法.整理如下：

单摆共振时做简谐运动，若从平衡位置开始计时，则振动的位移x=0.08sin(2πft)=0.08sinπt，振动的速度v=x′(t)=0.08πcosπt，可见速度的最大值vm=0.08π=0.25 m/s；

振动的加速度a=v′(t)=-0.08π2sinπt，可见加速度的最大值am=0.08π2=0.80 m/s2.

这种解法怎样？是否有耳目一新的感觉呢？所谓“教学相长”，我们这些当老师的是不是也应该感谢我们的学生呢？

三、脑洞大开，跃跃欲试

位移x对时间t求导是速度

速度v对时间t求导是加速度

由此想开去——

功W对时间t求导是什么？是功率P！

功W对位移x求导又是什么？是力F！

还有——

动量的变化△p对时间t求导等于合力F

角度θ对时间t求导等于角速度ω

电荷量q对时间t求导等于电流I

磁通量Φ对时间t求导等于感应电动势E

继续——

电势φ对距离d求导等于电势差U

电势差U对距离d求导等于场强E

势能Ep对距离r求导等于相应的保守力F

……

总之，只要一个物理量是相对于另一个物理量的变化率，那么这个物理量就可以运用导数来分析求解.

怎么样？脑洞大开了吧！是否有种跃跃欲试的冲动呢？那好，心动不如行动！下面再做两题：

题3 如图2所示，矩形线圈匝数为n，在匀强磁场中绕OO＇轴转动，设线圈的两个边长分别是L1和L2，转动时角速度是ω，在磁场的磁感应强度为B.

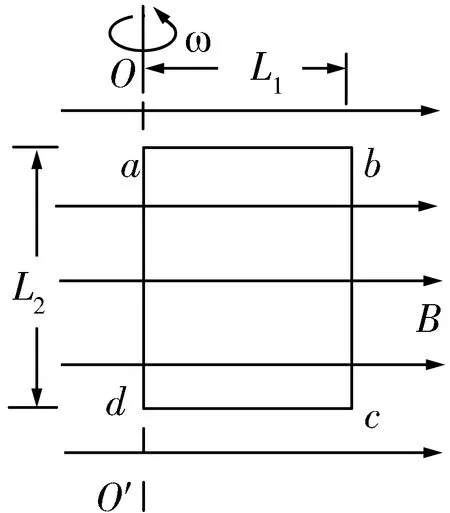
图2

试证明：在图示位置时，线圈中的感应电动势为E=nBSω，其中S=L1L2，为线圈面积.

本题一般做法如下：

线圈绕OO＇轴转动，线圈中长为L2的边都在切割磁感线，根据公式E=Blvsinθ可得：E=nBL2vsinθ，而图示位置θ=90°，切割速度为v=ωL1，代入可得：E=nBSω，其中S=L1L2，为线圈面积.

下面再用求导的方法来做：

当线圈在磁场中转动时，若从图示位置开始计时，则穿过线圈平面的磁通量瞬时值表达式为：φ(t)=Φmsinωt=BL1L2sinωt

每匝线圈中产生的感应电动势e0(t)=φ′(t)=BL1L2ωcosωt

故n匝线圈中产生的总的感应电动势e(t)=nBL1L2ωcosωt

图示位置t=0，E=nBSω，其中S=L1L2，为线圈面积.证毕.

两种方法相比，你不觉得用求导的方法显得更加简捷而畅快吗？

[1]张维善.普通高中课程标准实验教科书物理选修3-2[M].北京：人民教育出版社，2010(4):18.

[2]任满红翰元设计系列.高二物理.四[M].北京：现代教育出版社，2016(6):15.

[责任编辑：闫久毅]

2017-07-01

冯云周，1970年2月，男，河北隆尧，河北隆尧一中 ，中学高级，本科，物理教育.

G632

A

1008-0333(2017)28-0050-02