数学思想在函数中的应用

文/梅州市梅县区三乡中学 李晓文

数学思想在函数中的应用

文/梅州市梅县区三乡中学 李晓文

函数是初中数学的重点内容，是对初中知识的概括和总结，是联系初高中知识的纽带，是变量数学在初中数学的渗透，它使学生的思维从常量数学过渡到变量数学，函数知识在中学数学中有举足轻重的地位，而在函数知识中蕴含了丰富的数学思想，认真学习和掌握好这些数学思想，对提高学生数学素养具有重要的现实意义。

一、函数中的代数思维

在数学中使用代数思维，即用代数的方法解决问题，它要求分析问题中的等量关系，把问题表示为含有未知数的等式，把问题形式化。还可以利用等式的性质进行变形，但在变化过程中始终保持等量关系。对于这一数学思维方法，在函数中无疑可以得到强化。

1.方程与函数思想

函数与方程关系密切，初中阶段函数关系式可以看成是含有两个未知数的方程。因此，我们可以运用方程知识解决许多函数问题，如求函数图象与x轴、y轴的交点坐标，就是解函数或自变量为零时的方程等。因此我们可以利用一元二次方程根的判别式来判断两函数图象是否相交，判断二次函数的图象与x轴的交点情况等。

例1.已经抛物线y=x2-5mx+4m2（m为常数），求证：此抛物线与x轴一定有交点。

析：本题将函数与方程的判别式结合在一起。抛物线与x轴的交点必满足y=0，故只需证明x2-5mx+4m2=0的判别式大于或等于0即可。

2.建模与函数思想

在函数知识中出现了一类以函数知识为背景，具有创新性、开放性、针对社会热点，有强烈时代气息的函数应用题，解答此类问题的关键是将实际问题中的内在、本质的联系转化为数学问题，建立数学模型，从而求得实际问题的答案。

二、函数中的几何思维

1.图形与函数

在初中函数教学中，出现了从几何图形中确立函数关系式而利用函数性质的解决几何问题的数形结合的新题型。这类题主要利用几何图形的性质列出几何量之间的等式，再将某些几何量转化成函数的变量或自变量，最后用函数的性质解答问题。

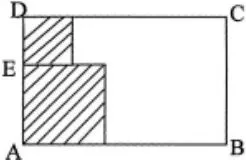
例2.如图，从一张矩形纸较短的边上找一点E，过这点剪下两个正方形，它们的边长分别是AE，DE，要使剪下的两个正方形的面积和最小，点E应选在何处？为什么？

析：考将这个几何问题转化另类二次函数模形来研究。

①首先探索取特殊值的情况

设AD=4，DE分别是2，1，0，当DE=2时，两个正方形面积的和最小，猜想：E是AD的中点时，两个正方形面积的和最小。

②证明猜想，设AD=t，ED=x，两个正方形的面积和为y，两个正方形的面积分别为x2，(t-x)2，则y=x2+(t-x)2，

得 y=2x2-2tx+t2， 配方得 y=2

本题运用了从特殊到一般的探究过程，在证明其一般性时运用数形结合思想 （图形→代数式→函数解析式）将问题转化为求二次函数的最值问题。

2.运动与函数

动态几何题是函数与运动相结合的典型题。动态几何题是以几何知识和几何图形为背景，渗入运动变化思想的一类题，通常是通过图形运动产生变量形成函数.

三、函数中的分类思维

分类讨论思想是根据数学本质属性的相同点和不同点，将数学研究对象分为不同种类的一种数学思想。初中数学分类讨论思想应用很广泛应用分类讨论，往往能使复杂的问题简单化。在函数的教学过程中我们要利用学生已有的认识基础，把生活中的分类迁移到数学中来，在数学教学中进行分类思想的渗透，挖掘教材提供的机会，把握渗透的契机。如

例3.函数y=ax2-ax+3x+1与x轴只有一个交点，求a的值与交点坐标。

分析：本题中函数是什么函数没有确定，故要根据初中学生已有的函数知识，根据a的不同取值，分别考虑此函数是一次函数或者二次函数两种情况。

解：当a=0时，为一次函数y=3x+1， 交点为 （-1/3， 0）；

当a不为0时，为二次函数y=ax2+(3-a)x+1， △ =b2－4ac=a2-10a+9=0，

解得a=1或a=9，交点为（-1，0）或 （9， 0）。

由上可见，在函数中蕴含着丰富的数学思想，在教学中我们要把它不断地向学生渗透这些思想，帮助学生掌握数学思想，提高其运用数学方法的能力。这是长期、复杂而细致的工作，中学数学教学中应全面研究教材中所蕴含的数学思想方法，探讨各种数学思想方法在不同阶段的教学要求，做到全面安排，逐步培养学生对数学思想的理解和运用能力。只有重视和加强数学思想方法教学，使数学知识的教学与思想方法的教学并重，数学教学的目标才能全面实现。

责任编辑 徐国坚