碳纤维多层织机打纬机构运动学分析与尺度综合

袁汝旺， 陈 瑞， 蒋秀明， 周国庆

(天津工业大学 天津市现代机电装备技术重点实验室, 天津 300387)

碳纤维多层织机打纬机构运动学分析与尺度综合

袁汝旺， 陈 瑞， 蒋秀明， 周国庆

(天津工业大学 天津市现代机电装备技术重点实验室, 天津 300387)

针对碳纤维多层织造过程中各层纬纱受力一致性需求，提出基于无急回特性曲柄摇杆机构串联的转动-转动-移动副(简称RRP)型基本杆组的轴向六连杆打纬机构，并给出刚体导引与机构几何关系相结合的尺度综合方法。在考虑钢筘极限位置和力传递性能的情况下，优化设计打纬机构，确定合理的机构尺寸和传动角。运动学仿真结果表明：钢筘极限位置和打纬动程的误差率均为0.06%，且在前死心时钢筘打纬加速度大，在后死心附近加速度变化较小，利于厚重织物打紧和机器降噪。轴向六连杆打纬机构驱动钢筘垂直作用于碳纤维多层织物的各层纬纱，受力均匀，其尺度综合方法为考虑织造工艺、运动学性能和机构尺寸等特定要求的打纬机构设计与优化提供一定的理论参考和实验数据。

碳纤维多层织机； 打纬机构； 运动学分析； 尺度综合方法

碳纤维多层织机主要用于织造具有一定厚度和较大幅宽的高性能复合材料预制件，特别是异形骨架型材，在航空航天、交通、风力发电等领域具有广阔的应用前景[1-2]。打纬是提高碳纤维织物性能的关键工艺，传统织机常采用四连杆[3]、六连杆[4]和共轭凸轮[5]打纬机构，钢筘安装在绕摇轴摆动的筘座脚上，其运动轨迹为圆弧；而碳纤维多层织物由多层经纱与多根纬纱交织构成，其厚度与刚度大，采用传统的圆弧轨迹打纬致使钢筘作用于各层纬纱的打纬力不均，且无法将全部纬纱推向织口并打紧织物[1-2]，因此，针对碳纤维多层织物纬纱受力一致性问题，国内外学者主要研究水平打纬机构的构型及其尺度综合方法，如：优化传统四连杆打纬机构的结构和尺寸参数，给出最佳参数对应的打纬力和机构效率等[6-8]；Badawi提出气缸驱动钢筘水平打纬，但受压缩空气影响，打纬机构响应速度慢且打纬力波动大[8]；还有学者对比分析碳纤维多层织物六连杆水平打纬机构的运动学特性及其对碳纤维纬纱切割、经纱磨损[9]和打纬动程[10]等指标参数的影响，并进行运动学建模与分析[9,11]，给出近似无急回特性六连杆打纬机构尺度综合方法[10]。

本文提出基于无急回特性的曲柄摇杆机构串联转动-转动-移动副(简称RRP)型Ⅱ级杆组的轴向六连杆打纬机构，在考虑打纬动程和机构压力角的情况下，利用刚体导引与曲柄摇杆机构几何关系相结合的方法进行机构运动学分析、尺度综合和参数优化，确定合理的机构尺寸参数，实现碳纤维多层织物的垂直均匀打纬。

1 工作原理

图1示出碳纤维多层织机打纬机构的工作原理。打纬机构由无急回特性的曲柄摇杆机构串联RRP型Ⅱ级杆组的六连杆实现，伺服电动机驱动曲柄1匀速转动，通过连杆2牵动摇杆3绕轴O3摆动；同时，摇杆3牵动连杆5驱动滑块6沿机架水平移动，钢筘与滑块固结，则钢筘产生的打纬力垂直作用织物截面，各层纬纱受力均匀一致。当打纬机构位于O1A1B1Q1P1位置时，钢筘位于极限初始位，即前死心位置，打纬力垂直均匀作用于织物；当打纬机构位于O1A2B2Q2P2位置时，钢筘位于极限终了位，即后死心位置。钢筘在前、后死心位置时，AB连线通过固定轴O1，即轴向打纬。在一个织造循环中，引纬全部完成后，主令时基信号伺服电动机控制间歇运转并驱动打纬机构。

注：1—曲柄；2—连杆；3—摇杆；4—机架； 5—连杆；6—滑块。图1 碳纤维多层织机打纬机构Fig.1 Beating-up mechanism of multi-layer loom for carbon fibers

2 轴向六连杆打纬机构尺度综合

为满足织造工艺和织机设计要求，机构尺度综合要兼顾机构尺寸和力传递性能，若给定尺寸要求，则以力传递性能最佳为优。打纬机构尺度综合分为摇杆滑块机构与曲柄摇杆机构2部分，其中摇杆滑块机构设计以力传递性能最佳为设计目标。

2.1摇杆滑块机构刚体导引综合

摇杆3与RRP型Ⅱ级杆组串联构成摇杆滑块机构，图2示出摇杆滑块机构的2个极限位置P1和Pj。

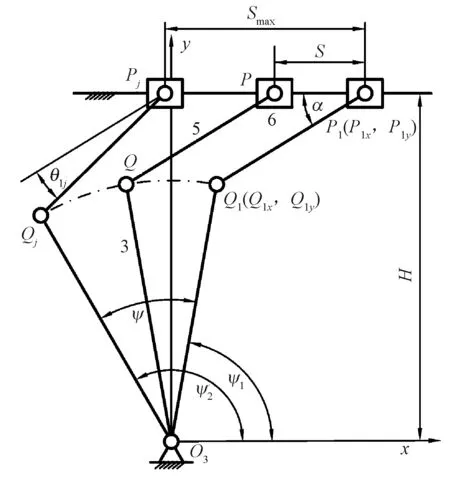
注：H—O3与滑块之间的垂直距离。图2 摇杆滑块机构Fig.2 Rocker-slider mechanism

图2中：滑块6位于前死心P1时，P1Q1与水平机架的夹角(压力角)为α；滑块6由前死心P1运动到后死心Pj，P1Q1的转角为θ1j，且滑块6的最大动程为Smax。 以O3为原点，建立坐标系xO3y，则P1Q1的斜率为

Q1xM-Q1y=N

(1)

式中：M=tanα；N=P1xtanα-P1y。

摇杆3作为联架杆的等长约束方程[12]为

Qj-O3TQj-O3=Q1-O3TQ1-O3

(2)

式中：Q1、O3和Qj分别为点Q1、O3和Qj的坐标矢量；j=2,3,…,n。

由刚体的平面运动可知：

(3)

式中，D1j为刚体自位置1至位置j的位移矩阵。

将式(3)代入式(2)并化简可得：

Q1xEj+Q1yFj=Gj

(4)

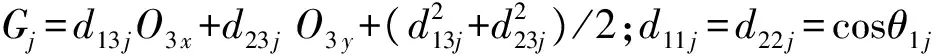
联立方程(1)、(4)，可得Q1的坐标：

(5)

令l3Q=O3Q,l5=PQ和ψ=ψ2-ψ1，则连杆长度与摆角分别为

(6)

(7)

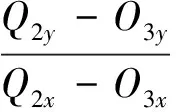
(8)

2.2无急回特性曲柄摇杆机构几何关系

图3示出无急回特性(行程速比系数K=1)的曲柄摇杆机构。图中，O3C与B1B2的中垂线交于C点，则中垂线与机架夹角β=∠CO3O1[β∈ (ψ/2,π/2)]。

图3 无急回特性的曲柄摇杆机构Fig.3 Crank-rocker mechanism of K=1

曲柄、连杆、摇杆和机架的长度分别为l1=O1A1、l2=A1B1、l3=O3B1和l4=O1O3，则几何关系的比率(λ)方程[13]分别为

(9)

曲柄回转中心O1坐标的比率方程为

(10)

当曲柄与机架共线时，得到2个最小传动角γ1min=∠A01B01O3和γ2min=π-∠A02B02O3，且

(11)

(12)

将式(9)代入式(11)、(12)得：

cosγ1min=cosγ2min=sinψ/2/sinβ

(13)

3 结果与讨论

3.1设计参数

考虑织造工艺、机构尺寸和力传递性能要求，取j=2，表1示出已知设计参数。

表1 给定的设计参数Tab.1 Given design parameters

注：[γmin]为最小允许用传动角；n为曲柄转速。

3.2摇杆滑块机构设计结果

由给定的设计参数可知，滑块位于前死心时， 摇杆滑块机构的传动角γ=90°-α=88.765°，力传递性能优越，打纬力大，适宜厚重的碳纤维多层织物。表2示出刚体导引尺度综合结果。

表2 刚体导引尺度综合结果Tab.2 Dimension comprehensive results of rigid-body guidance

数据表明，ψ的大小决定于钢筘的极限位置参数，与l3的长度无关。

3.3无急回特性曲柄摇杆机构设计讨论

当ψ为定值，最小传动角γmin和β的关系为β=arcsin [sin(ψ/2)/cosγmin]。图4示出γmin取不同值时β的变化情况。由图可知：当γmin=40°时，β=8.906°；当γmin=90°-ψ/2=83.195°时，β=90°，但实际β<90°，故γmin<83.195°；当γmin=76°时，β=29.354°，且γmin>76°时，β随γmin的增加而急剧增加，故γmin≤76°。因此，β宜在9°～30°范围内取值。

图4 γmin与β的关系(ψ=13.610°)Fig.4 Relationship between γminand β (ψ=13.610°)

当ψ=13.610°时，λ1=sin(ψ/2)=0.119。表3示出γmin和参数比率随β变化的结果。数据表明，γmin和参数比率随β增大而增加，负号表示方向相反。当β=15°时，γmin>[γmin]。当β≤19°时，λ4<3，为短牵手；当20°≤β≤30°时，3<λ4<6，为中牵手。λx和λy位于平行于Q1Qj的直线上，且λx的变化速度比λy快。

令l3=550 mm，则l1=l3sin(ψ/2)=65.168 mm。 表4示出β为不同值时的曲柄摇杆机构设计结果。数据表明：曲柄摇杆机构的连杆尺寸随β增大而变大，且曲柄回转轴坐标O1x和O1y位于平行于Q1Qj的直线(y=0.115 4x+549.75)上，且O1x的变化速度比O1y快。

依据表2、4的设计结果，利用Ⅱ级杆组法依次分析刚体(构件1)、RRR型Ⅱ级杆组(构件2～3)，RRP型Ⅱ级杆组(构件5～6)，由滑块6的运动规律得到打纬动程及其变化情况。图5示出β取值不同时的钢筘运动规律。由图可看出：β取值变化均满足打纬动程要求；β越小，在前死心位置筘座运动速度越快，利于织物打紧，但对称性差；β越小，打纬时筘座加速度值越大，对打紧织物有利，但是筘座加速度变化均匀性差，织机振动厉害，不利于高速。

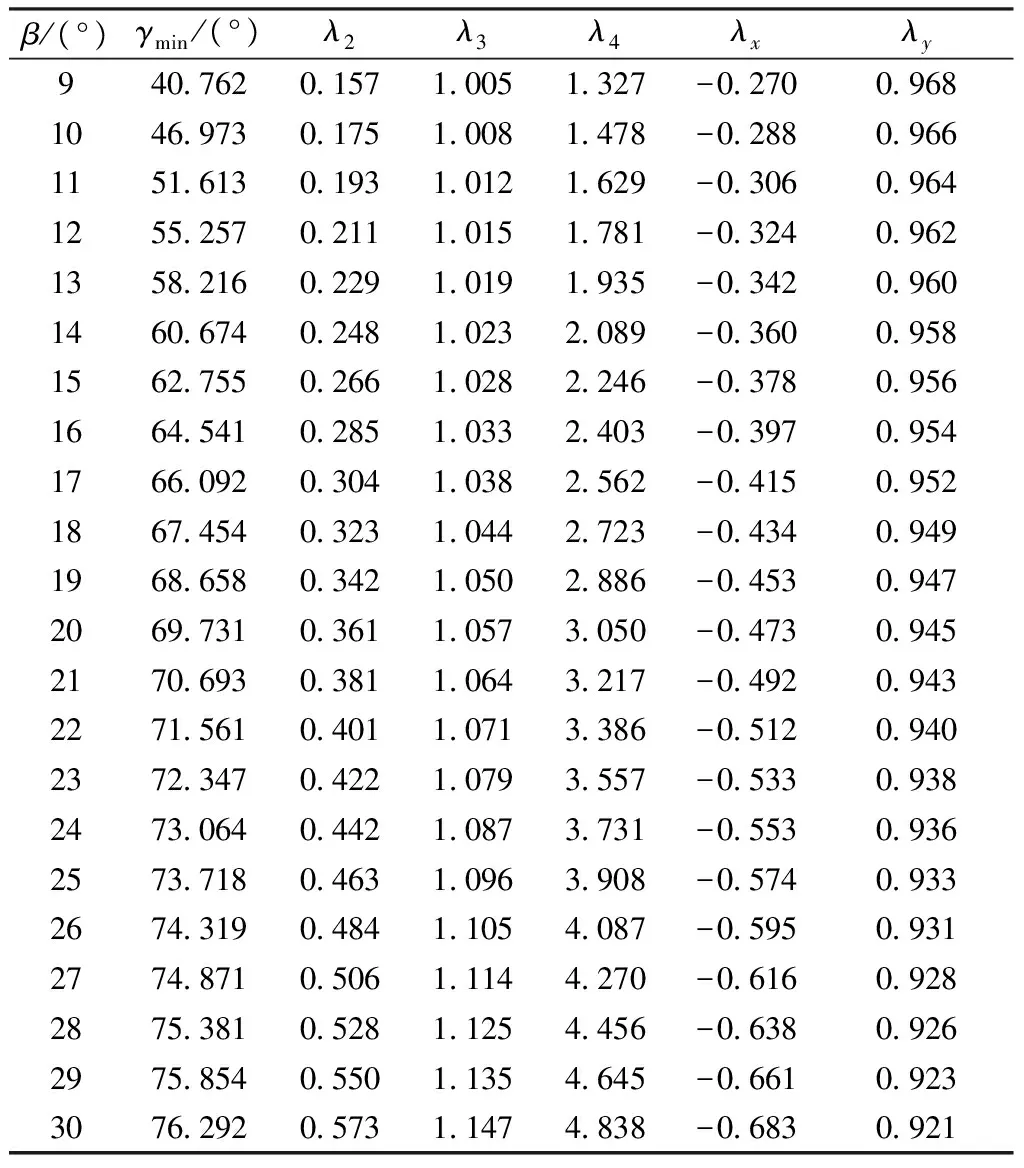
表3 不同β值的γmin和参数比率Tab.3 γmin and parameter ratios of various β values

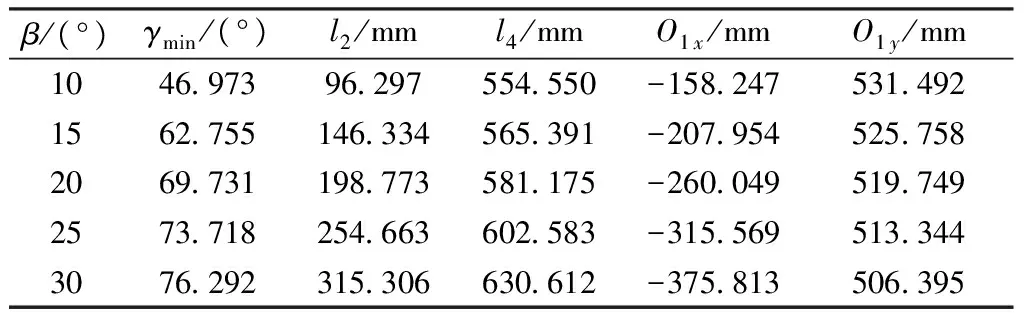
表4 曲柄摇杆机构设计结果Tab.4 Design results of crank-rocker mechanism

3.4打纬机构设计参数优化

针对碳纤维多层织机低速且织物厚重的特点，考虑机构尺寸、制造精度和力传递性能等因素，表5示出打纬机构的设计优化结果。

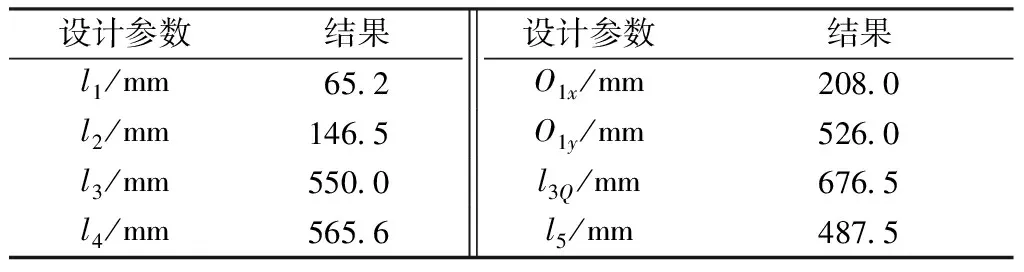
表5 打纬机构优化结果Tab.5 Optimization results of beating-up mechanism

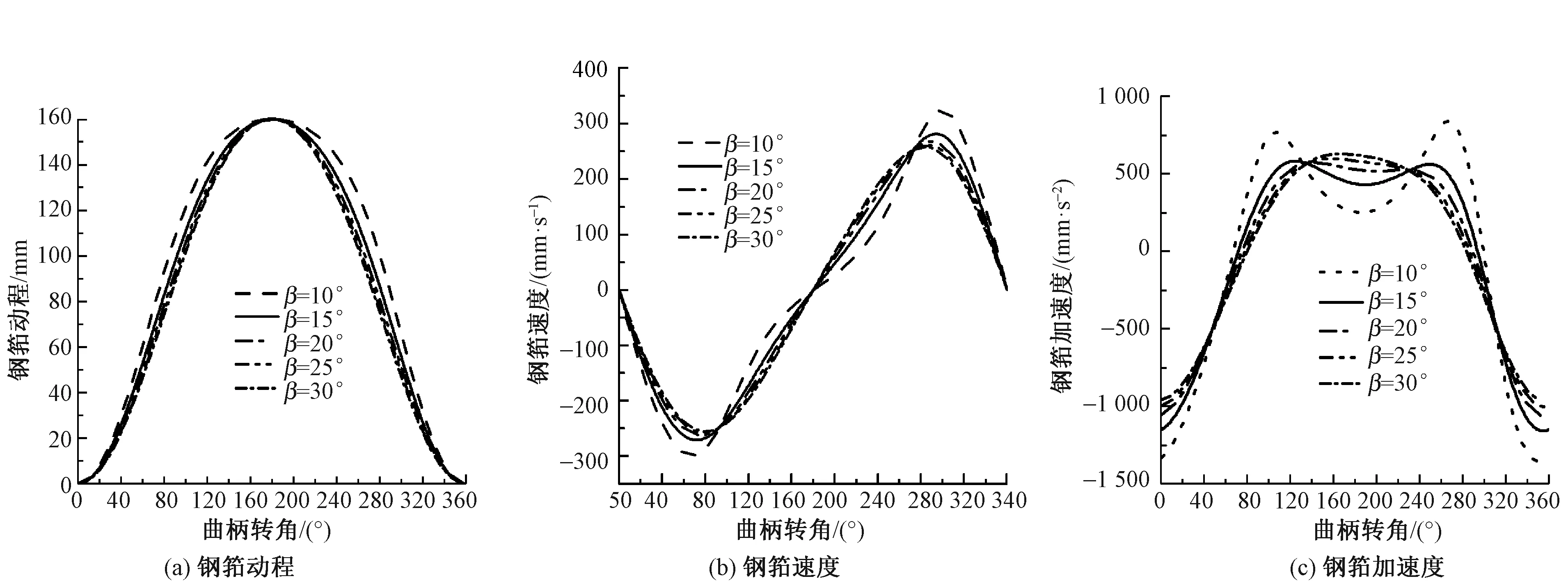
图5 不同β值的打纬机构运动规律Fig.5 Movement of beat-up mechanism for various β values.(a)Reed traverse；(b)Reed velocity； (c)Reed acceleration

在坐标系xO3y中对轴向六连杆打纬机构进行运动学分析，图6示出钢筘运动规律。由图可知：钢筘运动到2个极限位置的坐标分别为P1x=490.3 mm、P2x=330.2 mm，最大动程Smax=P1x-P2x=160.1 mm，且动程与位置坐标的误差率均为0.06%，利于织物打紧；钢筘运动到前死心时，加速度为-1 159.7 mm/s2，且在后死心附近加速度变化较小，利于碳纤维多层织物打紧和机器降噪。

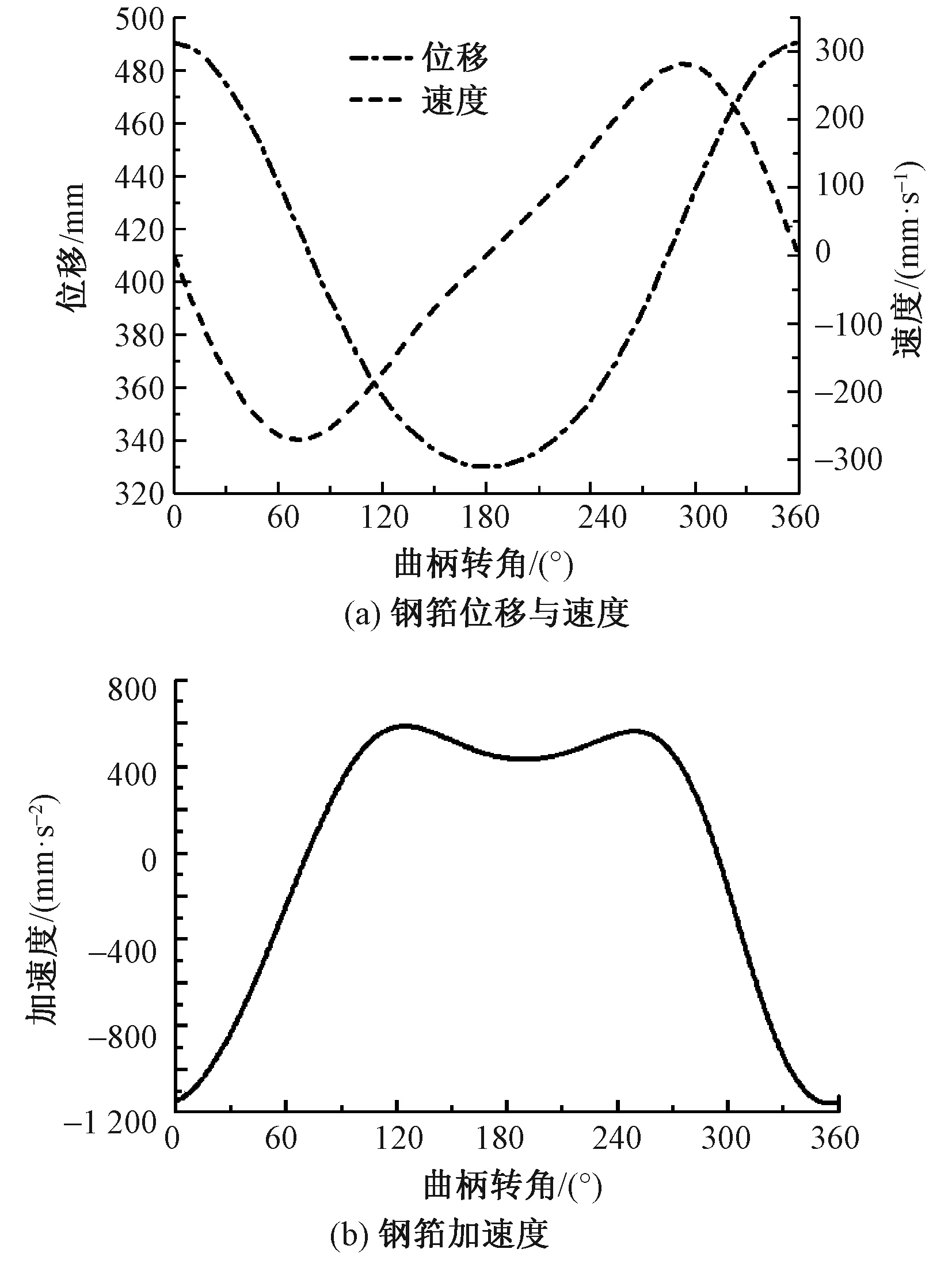
图6 钢筘的运动规律Fig.6 Movement curve of reed.(a)Reed displacement and velocity；(b)Reed acceleration

4 结 论

1)基于K=1的曲柄摇杆机构串联RRP型Ⅱ级杆组的轴向六连杆打纬机构实现钢筘水平运动，且打纬力均匀垂直作用于织物组织截面，满足所有纬纱受力一致的需求。

2)针对轴向六连杆打纬机构提出刚体导引与曲柄摇杆机构的几何关系相结合尺度综合方法。分析结果表明：摇杆摆角的大小取决于钢筘的极限位置参数，与摇杆长度无关，且调整摇杆铰接点位置可改变钢筘极限位置和打纬动程；摆角确定后，曲柄摇杆的机构尺寸与最小传动角均随夹角的增加而增加，当机构传动角不小于最小许用传动角时，调整夹角大小以获得合理的机构尺寸。

3)轴向六连杆打纬机构优化结果表明：钢筘运动到2个极限位置与动程的误差分别为0.3、0.2、0.1 mm，但误差率均为0.06%；钢筘位于前死心时，加速度为-1 159.7 mm/s2，在后死心附近加速度变化较小，利于碳纤维厚重织物打紧和机器降噪。

FZXB

[1] MOUNTASIR A, HOFFMANN G, CHERIF C. Development of multilayered woven panels with integrated stiffeners in the transverse and longitudinal directions for thermoplastic lightweight applications[J]. Textile Research Journal, 2013, 83(14):1532-1540.

[2] MOUNTASIR A, HOFFMANN G, CHERIF C. Development of weaving technology for manufacturing three-dimensional spacer fabrics with high-performance yarns for thermoplastic composite applications: an analysis of two-dimensional mechanical properties[J]. Textile Research Journal, 2011, 81(13):1354-1366.

[3] EREN R, AYDEMIR A. An approach to kinematic design of four-bar sley drive mechanisms in weaving[J]. Journal of the Textile Institute, 2004, 95(1):193-205.

[4] EREN R, AYDEMIR A. Kinematic design method for six-bar linkage sley drive mechanisms in weaving[J]. Indian Journal of Fiber & Textile Research, 2005, 30(3):243-251.

[5] TANG Xuemei. Calculation algorithm for kinematics accuracy reliability of conjugate cams beating-up mechanism[J]. Journal of Information & Computational Science, 2014, 11(18): 6787- 6793.

[8] BADAWI Msss. Development of the weaving machine and 3D woven spacer fabric structures for lightweight composites materials[D]. Dresden: Technischen Universität Dresden, 2008:120-129.

[9] 李佳. 立体织机经纱系统和打纬机构的设计[D]. 上海: 东华大学, 2013:25-40.

LI Jia. The design of warp system and beating-up mechanism in 3-D weaving machine [D]. Shanghai: Donghua University, 2013:25-40.

[10] 韩斌斌, 王益轩, 陈荣荣,等. 基于ADAMS的三维织机平行打纬机构的设计研究[J]. 产业用纺织品, 2015(10):22-26.

HAN Binbin, WANG Yixuan, CHEN Rongrong, et al. Design of the parallel beating-up mechanism for 3-D weaving machine based on ADAMS[J]. Technical Textiles, 2015(10):22-26.

[11] 刘薇, 蒋秀明, 杨建成,等. 碳纤维多层角联机织装备的集成设计[J]. 纺织学报, 2016, 37(4):128-136.

LIU Wei, JIANG Xiuming, YANG Jiancheng, et al. Integration design of carbon fiber multi-layer diagonal weaving equipment[J]. Journal of Textile Research, 2016, 37(4):128-136.

[12] 华大年, 华志宏. 连杆机构设计与应用创新[M]. 北京: 机械工业出版社, 2008:127-135.

HUA Danian, HUA Zhihong.Design and Application Innovation of Linkage Mechanism[M]. Beijing: China Machine Industry Press, 2008:127-135.

[13] 王长钧.K=1的平面曲柄摇杆机构最佳传动角设计原理及其参数选择[J]. 南京林业大学学报(自然科学版), 1989, 13 (2):69-72.

WANG Changjun. The design principle based on the opitmum transmiss angle ofK=1 crank-rocker mechanism and its seleciton of parameters[J]. Journal of Nanjing Forestry University (Natural Science Edition), 1989, 13(2):69-72.

Kinematicsanalysisanddimensionsynthesisofbeating-upmechanismforcarbonfibermulti-layerloom

YUAN Ruwang， CHEN Rui， JIANG Xiuming， ZHOU Guoqing

(TianjinKeyLaboratoryofAdvancedMechatronicsEquipmentTechnology，TianjinPolytechnicUniversity,Tianjin300387，China)

The axial six-bar linkage beating-up mechanism based on the crank and rocker mechanism with non-quick return characteristics series-connected with the basic linkage group in two revolute joints and one prismatic joint model was proposed aiming at the demand of consistent force-loading to the weft yarn on each layer during the carbon fiber multilayer weaving process. The dimension comprehensive method with the combination of rigid body guidance and the mechanism geometrical relations was also provided. Taking into consideration on the limit position of reed and the force transfer property, the design of beating-up mechanism was optimized, and the feasible size of machine and transmission angle were determined. Simulation results of kinematics show that the error rate of both the reed limit position and the movement of beating-up mechanism is 0.06%. The reed beating-up has a high acceleration at the front dead center, and the acceleration has few changes near the back dead center, which is beneficial to the tightening of heavy fabric and machine noise reduction. Driven by the axial six-bar linkage beating-up mechanism, the reed exerts perpendicular force to weft yarn on each layer of carbon fiber multilayer fabric. Each layer of the fabric is subjected to even force. The dimension comprehensive method provides a certain theoretical basis and experimental data for the design and optimization of beating-up mechanism taking account of specific requirements such as weaving technology, kinetic performance and machine size.

carbon fiber multi-layer loom；beat-up mechanism；kinematics analysis；dimension comprehensive method

10.13475/j.fzxb.20170102406

TS 103.1

A

2017-01-11

2017-05-31

国家科技支撑计划重点项目(2011BAF08B02)

袁汝旺(1979—)，男，讲师，博士。研究方向为纺织机械设计与机构学。E-mail：yuanruwang@tjpu.edu.cn。