关于无线传感器网络定位算法仿真*

何 涛， 包亮强， 赵长财

(1.兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070； 2.卡斯柯信号有限公司，上海 200071； 3.兰州交通大学 电子与信息工程学院，甘肃 兰州 730070)

关于无线传感器网络定位算法仿真*

何 涛1， 包亮强2， 赵长财3

(1.兰州交通大学自动化与电气工程学院，甘肃兰州730070；2.卡斯柯信号有限公司，上海200071；3.兰州交通大学电子与信息工程学院，甘肃兰州730070)

针对无线传感器网络(WSNs)节点定位的问题，提出了一种通过构建粒子群机制的量子神经网络模型优化距离矢量跳跃(DV-HOP)的定位算法(PSO-QNN),根据传统DV-HOP所得到的平均距离和实测节点距离构建量子神经网络模型，并通过粒子群算法对平均距离进行训练，从而得到较优平均值，实现了对DV-HOP算法的优化。算法缩短了传统人工神经网络的训练时间，并且加快了收敛速度。仿真结果表明：与传统DV-HOP算法相比，所提出的PSO-QNN算法能够减少约20 %的定位误差，定位精度显著提高。

无线传感器网络； 量子神经网络； 粒子群优化算法； 距离矢量跳跃算法

0 引 言

近年来，无线传感器网络(wireless sensor networks, WSNs)的研究成果在环境检测、目标跟踪、军事等领域广泛使用[1]。随着WSNs理论研究和实际应用的深入结合[2,3]，目前对于WSNs的研究主要在网络节点的能耗、节点部署和节点定位三个方面，其中节点定位的研究是传感器网络在很多应用中的前提[4]。

在WSNs的定位过程中根据节点位置是否需要测量，将定位算法分为基于测距的(range-based)定位算法和无需测距的(range-free)定位算法[5]。典型的无需测距的定位算法有质心(Centroid)法、近似三角形内点测试(approximate point-in-triangulation test,APIT)、距离矢量跳跃(distance vector-hop,DV-HOP)[6]、Amorphous等,具有实现简单、不需要额外的硬件、网络生存能力强、成本低等特点，经常被用于WSNs定位中。本文主要针对无须测距的DV-HOP算法进行相关研究。传统DV-HOP算法在实现WSNs节点定位的过程中主要依靠对平均跳距的估计来实现定位。网络中的不良节点会导致获取的跳数信息不合理，以致于根据跳数信息所得到的平均跳距存在较大误差，从而使得WSNs节点定位的精度和效率急剧下降，定位过程具有模糊性和不确定性。

因此，本文用粒子群优化(particle swarm optimization,PSO)算法作为量子神经网络(quantum neural network,QNN)的学习机制[6,7],提出了一种PSO-QNN的WSNs定位算法。通过将两种算法相结合，构造了一个学习时间短、收敛速度快、寻优精度高的节点定位模型。通过训练，量子神经网络得到最佳的初始化权值和阈值。将该模型结合运用到DV-HOP算法中，得到较优平均跳距值，从而提高了节点的定位精度。通过Matlab仿真证明该算法在定位精度和效率方面有了很大的改善。

1 DV-HOP算法[8]

图1为跳距原理的具体示意。

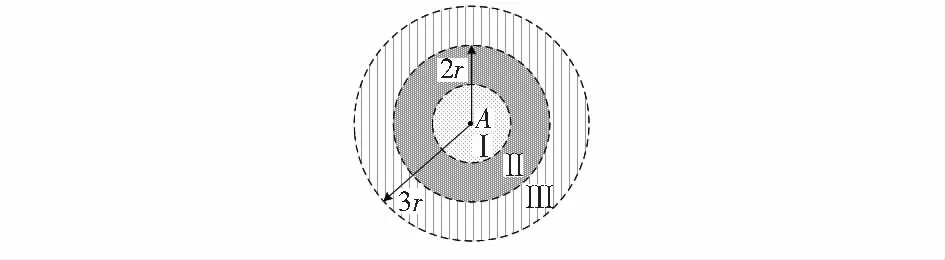
图1 跳距原理

图1中A为锚节点，通信半径为r，I,II,III分别为锚节点A的1,2,3跳的约束区域。

DV-HOP算法具体分为3个阶段：1)锚节点向整个WSNs广播自身在网络中的位置信息和跳数，设跳数的初始值为0，待定位节点记录每个锚节点的最小跳数值，并将跳数值加1并转发给邻居节点，此刻所有节点通过距离矢量交换协议得到自身到锚节点的最小跳数；2)每个锚节点根据阶段一记录的与其他锚节点的位置信息和相距跳数，计算每个锚节点与其他锚节点之间的平均每跳实际距离

(1)

式中 (xi,yi),(xj,yj)分别为节点i和j的位置坐标;hij为锚节点i和j,i≠j之间的跳段数，然后将每跳平均距离作为校正值在整个WSNs内广播，当待定位节点接收到第一个校正值后,保存，之后不再接收其他校正值，根据校正值，将待定位节点到锚节点的最小跳数换算为到锚节点的距离；3)待定位节点得到三个或者三个以上的锚节点的位置时，通过三边或者多边测量法得到待定位节点的位置。

2 基于PSO-QNN的DV-HOP算法

2.1 量子神经网络[9～11]

2.1.1 经典反射传播神经网络模型

反向传播(back propagation,BP)神经网络由三层结构组成：输入层、隐含层和输出层。在该模型中输入层LA由m个节点组成，输出层LC有n个节点，隐含层 LB的节点数目为p。 同层节点之间不相连，相邻层节点全互连。

传统BP神经网络隐含层LB的节点输出为

br=f(WTX-θ),r=1,2,3,…,p

(2)

输出层LC的节点输出为

cj=f(VTB-φ),j=1,2,3,…,n

(3)

式中对应关系f为Sigmoid函数(也称为S型生长曲线)即f(x)=(1+e-x)-1;X为神经网络的输入，输入层的神经元为ai，隐含层的神经元为br，输出层的神经元为cj。Wir为输入层神经元到隐含层神经元之间的连接权值;Vrj为隐含层神经元到输出层神经元之间的连接权;θ为隐含层的阈值;φ为输出层的阈值。

2.1.2 量子神经网络模型

将多个Sigmoid函数进行叠加，一个隐含层神经元即可表示多个量级，从而构建成多层结构的激励函数，使得该网络的模糊性大幅增加，则此时隐含层输出为

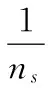
(4)

式中ns为量子间隔数目，ns的选择与故障数目相同;αm为陡度因子;θγ为量子间隔。

多层激励函数的量子神经网络模型训练算法仍采用梯度下降法。在该训练过程中，更新的内容包括不同层神经元之间的连接权值和隐含层各个神经元之间的量子间隔。其中连接权值的更新与BP神经网络无异，隐含层神经元的量子间隔更新算法如下：

对于模式类矢量Cm(m为模式类数目，即输入层的神经元个数)，那么隐含层第j个神经元的输出变量为

(5)

(6)

式中Oj,k为输入矢量为xk时，隐含层第j个神经元的输出。

(7)

式中η为学习率;αm为陡度因子。

2.2 粒子群优化算法[12]概述

假设有一个N维的目标搜索空间，由m个粒子组成，第p个粒子在d维空间中的位置为

Lp=[lp1,lp2,lp3,…,lpd],p=1,2,…,m

(8)

飞行速度为

Vp=[vp1,vp2,vp3,…,vpd],p=1,2,…,m

(9)

适应值为

fitnessp=f(Lp)

(10)

该算法中具有2个极值：各个粒子本身所找到的最优解pbest；整个粒子群所发现的最好位置gbest。在该算法中的粒子p在d维空间中位置和速度按照如下迭代方程进行更新

(11)

(12)

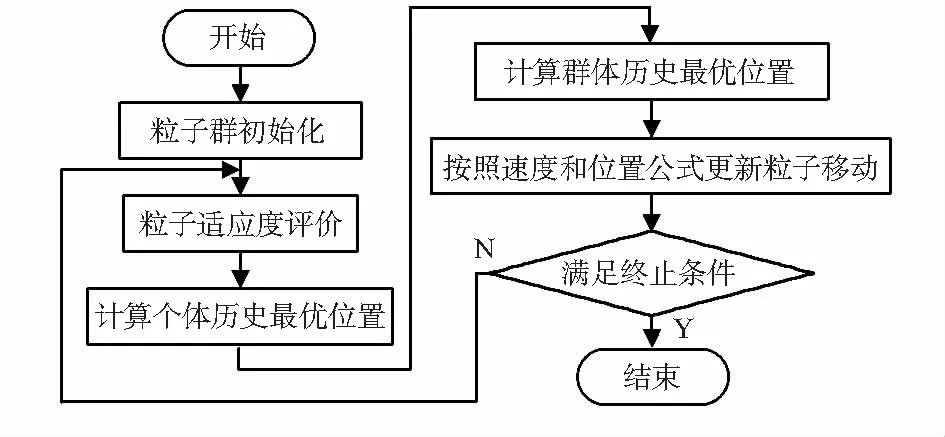
图2 粒子群优化算法流程

2.3 算法实现步骤

设锚节点为P个，待定位节点为M个，则整个WSNs节点定位的步骤如下：

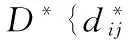
2)利用PSO算法极强的寻优能力，搜寻每个粒子的全局最优解gbest；

3)建立模型之后，将锚节点和待定位节点在WSNs中进行分布，每个锚节点定时在WSNs中广播自身的相关参数，包括节点坐标、量子神经网络参数。所有节点通过距离矢量交换协议得到自身到锚节点的最小跳数；

4)根据所记录的每个锚节点到其他锚节点的位置信息和跳数，利用式(1)计算平均每跳实际距离；

7)当待定位节点接收并保存第一个校正值后，将其转发给相邻节点，待定位节点根据校正值根据已记录的跳数信息计算与每个锚节点的跳段距离值；

8)待定位节点得到3个或者3个以上的锚节点的位置时，通过三边或者多边测量法得到待定位节点的位置。

2.4 算法具体描述

2.4.1 PSO训练QNN算法

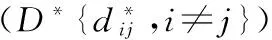
2.4.2 优化QNN的初始权值及量子间隔

首先要选取对应的数据对QNN进行学习和训练[13]，以此形成实践模型应用于WSNs定位中。本文通过PSO对QNN的参数进行训练。其中需要训练的参数为隐含层节点所包含的对QNN的参数即为m×p个θ和p个λ，输出层节点包含的n×p个θ和n个λ。其中，m为输入层节点的个数，p为隐含层节点的个数，n为输出层节点的个数，θ为连接神经元之间的权值，λ为阈值。将神经元之间的连接权值映射为PSO算法中的粒子的位置，则此时粒子群的维度就是m×p+n×p+p+n。初始化种群之后，按照算法步骤进行迭代。直到产生均方差(mean square error,MSE)最小的粒子位置，此时该粒子位置的各维度值就是得到的最优的初始权值和阈值。

设训练的样本数量为N，则网络的MSE

(13)

式中tij为样本i在第j个输出端的的期望输出值。

2.4.3 三边或多边测距

在三边或者多边测量法中设待定位节点的坐标为(x，y)，锚节点的坐标为(x1，y1)，(x2，y2)，(x3，y3),…,(xk，yk)，则待定位节点到各锚节点的距离为d1，d2，d3,…,dk

(14)

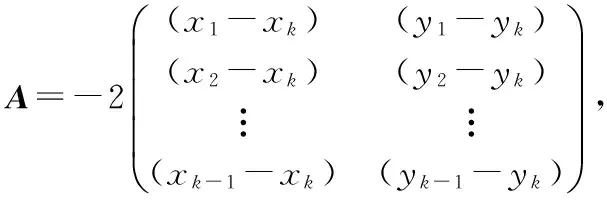
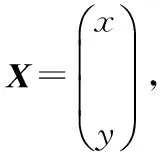
X=(ATA)-1ATB

(15)

由式(15)可得待定位节点的位置坐标。

3 仿真结果

实验在 Intel(R) Core(TM)i3—2370M CPU，主频2.40,2.40 GHz，4 GB 内存平台，Matlab7.0仿真环境中进行。仿真实验中，构建100 m×100 m的节点定位检测区域。该区域中部署150个传感器节点，节点的通信半径r=25 m，节点随机部署在该区域中。在PSO算法中，种群的初始化数目为m=40，最大迭代次数为Q=100,学习因子c1=c2=1.8，锚节点和待定位节点分布如图3。

图3 节点分布

3.1 锚节点数对定位误差的影响

根据本文算法的实施步骤对节点进行定位，根据仿真结果得到平均定位误差[14,15]，其中平均定位误差定义为

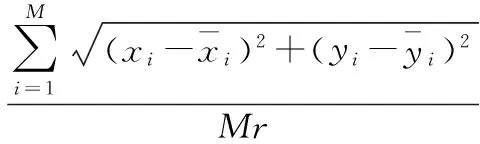
(16)

由图4可以看出：在相同环境下,本文算法的定位误差较传统DV-HOP算法的误差要低很多。选择加权质心算法作为对比算法，可以看出3种算法随着锚节点个数的增加平均定位误差均呈现下降的趋势。本文算法的平均定位误差约为26 %，加权质心算法的平均定位误差约为38 %，传统DV-HOP算法的平均定位误差约为48 %。本文算法较传统DV-HOP算法的平均定位误差降低了约20 %。

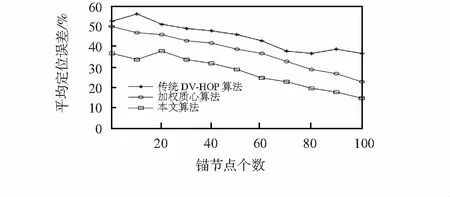
图4 定位误差对比

3.2 待定位节点数对定位误差的影响

由于跳数转换为距离的过程会产生较大误差，因此,该算法在实施过程中要求待定位节点需要很高的密度。仿真结果如图5所示，随着待定位节点的密度增加，3种算法所需的持续时间也随之下降，而本文算法所需的时间较传统DV-HOP算法减少了约100 ms。

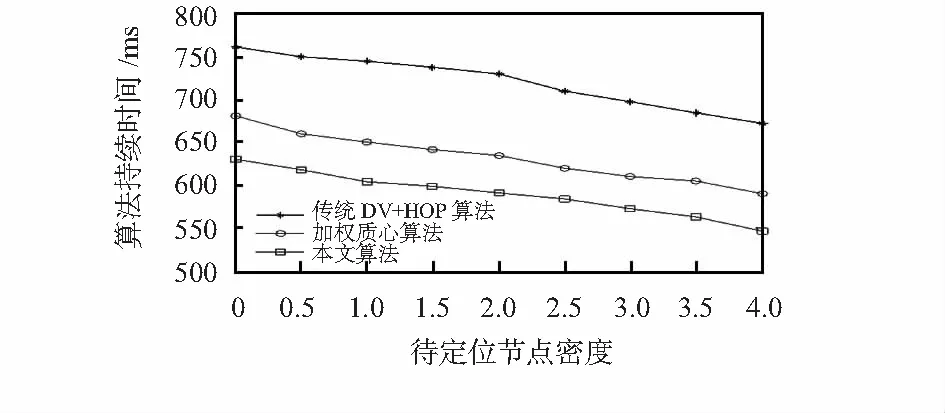
图5 待定位节点密度对算法持续时间的影响

3.3 连通度对定位误差的影响

在DV-HOP算法中，节点之间可以直接通信传输信息。连通度主要反映了锚节点数量及通信半径两者的关系，实验通过分析连通度的变化比较定位误差。由图6可以看出，随着连通度的增加，三者的平均定位误差大体上呈下降趋势。在相同的连通度下，本文算法的定位误差在三者中最小。

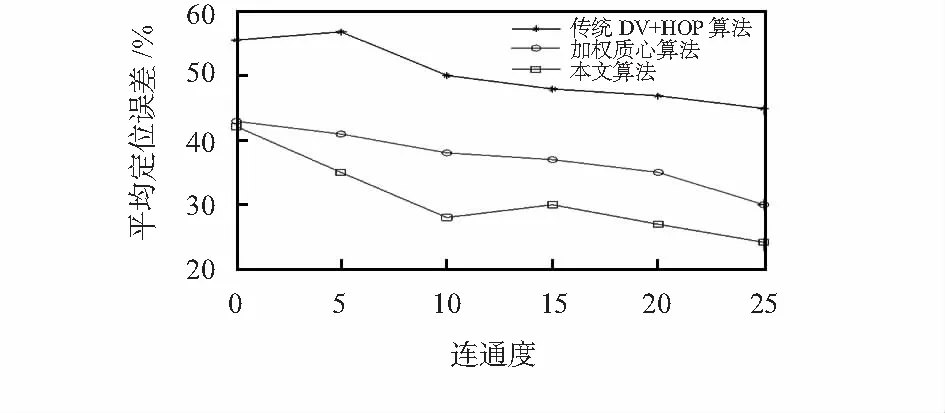
图6 不同连通度对平均定位误差的影响

4 结束语

针对基于DV-HOP算法在WSNs节点定位过程中易受外界环境因素影响而导致测量距离数据存在较大误差的问题，提出了PSO-QNN算法，与传统的BP神经网络相比，QNN加快了算法的收敛速度，在模糊性方面的表现更为突出。本文通过将PSO算法作为QNN的学习算法，构建了PSO-QNN网络模型，进一步对DV-HOP算法进行改进。通过仿真实验对所得到的数据从三方面进行分析，结果表明：本文算法的定位精度有了很大的提升，可达20 %左右，证明了本文算法在节点定位方面的有效性。

[1] Shi H,Wang W.Game theory for wireless sensor networks:A survey[J].Sensors,2012,12(7):9055-9097.

[2] 马祖长，孙怡宁，梅 涛.无线传感器网络综述[J].通信学报，2004,25(4)：114-124.

[3] 李鹏程，廖 波，罗 娟，等.无线传感器网络中一种移动节点定位算法[J].小型微型计算机系统，2008,29(11)：2051-2054.

[4] 王 学，李 蒙，宋书中.锚节点选择和距离修正的DV-HOP定位算法[J].计算机测量与控制，2012,20(12)：3317-3320.

[5] 张 品，毛文敏，徐 静.一种基于迭代投票的无线传感器网络安全定位算法[J].传感器与微系统，2015,34(12)：118-120.

[6] ZeKavat Buehrer．Handbook of position location:Theory,practice and advance[M].NJ:Wiley & Sons,2012:359-395．[7] 李盼池.量子计算及其在智能优化与控制中的应用[D].哈尔滨：哈尔滨工业大学，2009.

[8] 石为人，贾传江，梁焕焕.一种改进的无线传感器网络DV-Hop定位算法[J].传感技术学报，2011,24(1)：83-87.

[9] 张翼鹏，陈 亮，郝 欢.一种改进的量子神经网络训练算法[J].电子与信息学报，2013,35(7)：1630-1635.

[10] 盖怀存，张小锋，江泽涛.基于量子神经网络的人脸识别技术研究[J].计算机工程与应用，2010,46(8)：187-189.

[11] 付丽辉.一种基于改进的量子神经网络的语音降噪方法[J].信息与控制，2010,39(4)：466-471.

[12] 李 晓,黄 纯.电力系统故障诊断的量子粒子群优化算法[J].电力系统及其自动化学报，2011,23(4)：61-66.

[13] 石晓伟，张会清，邓贵华.基于 BP 神经网络的距离损耗模型室内定位算法研究[J].计算机测量与控制，2012,20(7)：1944-1947.

[14] 陶志勇，魏 强，刘 影.多功率锚节点辅助的DV-Hop定位算法[J].计算机工程与应用，2014,50(21)：121-124.

[15] 王 颖，石昊旸.改进的无线传感器网络DV-Hop定位算法[J].计算机工程，2012，38(7)：66-69.

SimulationstudyonlocalizationalgorithmforWSNs*

HE Tao1, BAO Liang-qiang2, ZHAO Chang-cai3

(1.SchoolofAutomationandElectricalEngineering,LanzhouJiaotongUniversity，Lanzhou730070，China;2.CASCOSignalCoLtd，Shanghai200071，China;3.SchoolofElectronicandInformationEngineering,LanzhouJiaotongUniversity，Lanzhou730070，China)

Aiming at wireless sensor networks(WSNs)node localization problem,a new localization algorithm is proposed by building quantum neural network model for particle swarm mechanism to optimize localization algorithm of DV-HOP,particle swarm optimization-quantum neutral network(PSO-QNN).The algorithm constructs quantum neural network model according to average distance obtained by traditional DV-HOP and distance of measured actual node,and through the particle swarm algorithm to train the average distance,so as to get better average,value to achieve the optimization of DV-HOP algorithm.The combination algorithm shortens the training time of the traditional artificial neural network,and speeds up the convergence rate.Simulation results show that compared with the traditional DV-HOP algorithm,the proposed PSO-QNN algorithm can reduce the positioning error of about 20 %,and the positioning precision is significantly improved.

wireless sensor networks(WSNs); quantum neural network(QNN); particle swarm optimization(PSO)algorithm; DV-HOP algorithm

10.13873/J.1000—9787(2017)11—0143—04

TP 393

A

1000—9787(2017)11—0143—04

2017—01—05

中国铁路总公司资助项目(2016X003—H)

何 涛(1977 -)，男，博士，教授，主要从事交通信息工程及控制研究工作,E—mail:hetao@mail.lzjtu.com。

赵长财(1991-)，男，通讯作者，硕士研究生，主要研究方向为电子与通信工程，E—mail:1193702476@qq.com 。