基于IDCS能量优化的船舶舵/翼舵航向保持控制*

刘 胜， 宋颖慧， 贾云璐

(哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001)

基于IDCS能量优化的船舶舵/翼舵航向保持控制*

刘 胜， 宋颖慧， 贾云璐

(哈尔滨工程大学自动化学院，黑龙江哈尔滨150001)

船舶舵/翼舵能够有效提高翼面的升力系数，减小系统能耗，但操控面的增多会带来角度分配问题。根据航向控制机理，通过航向检测装置检测到的航向角，计算出系统的艏摇扶正力矩，并建立舵/翼舵角度优化分配规则，在系统驱动能量损耗指标下，提出了一种改进的动态布谷鸟搜索(IDCS)算法，提高了系统寻优过程的全局探测及局部搜索能力，实现舵角/翼舵角度的智能优化分配。仿真结果表明：舵/翼舵能够避免了单体舵出现的舵速饱和现象，提高了航向控制效果并有效降低系统能耗；同时相较于遗传算法(GA)和布谷鸟搜索(CS)算法，基于IDCS算法的舵角/翼舵角分配策略也能够取得更小的能耗指标，从而证明了所提出的算法有效性和工程应用价值。

船舶； 舵/翼舵； 改进的动态布谷鸟搜索算法； 能量优化； 航向保持控制

0 引 言

船舶在海上航行时，由于受到风浪流的干扰，会产生偏航现象，不仅会引起船舶的航行安全问题，同时由于频繁操舵而增加了船舶的航行成本。自动舵是操纵船舶的关键性设备，用以提供航向保持所需艏摇扶正力矩[1]。随着船舶大型化、高速化及高性能化的发展趋势，要求自动舵系统能够保持较高的航向控制精度[2～4]。为了寻求更为有效的操控装置，对带有襟翼的舵/翼舵的研究受到了广泛重视[5～7]。采用舵/翼舵改善船舶航向控制效果，主要通过减小主舵的运动幅度，使所需的控制力矩由小控制面翼舵运动完成，从而节省能耗，提高系统可靠性，充分挖掘了有限面积舵/翼舵的操控能力。

目前对于舵/翼舵的研究多注重对水动力的分析，对于多操纵面控制力矩分配问题的相关研究较少[8，9]。针对舵/翼舵产生的控制力矩和舵角/翼舵角存在多元多值函数关系，文献[7]中利用遗传算法(genetic algorithm,GA)对舵角翼舵角进行了优化分配，改善了船舶航向控制性能。该方法进行角度优化分配虽然简单易行，但有时容易陷入局部最优解，影响系统的可靠性。为了能够有效改善舵角/翼舵角的优化能力，避免搜索过程中陷入局部极小解。本文提出了采用改进的动态布谷鸟搜索(improved dynamic cuckoo search,IDCS)算法寻优最佳舵/翼舵角度分配策略，在满足系统操控性能的前提下，减小主舵的运动幅度及转动频率，有效降低舵/翼舵系统的能量消耗。

布谷鸟搜索(CS)算法是一种新兴的全局启发式搜索方法[10～15]，具有简单、参数少、易于实现等优点，由于引入了Levy Flight搜索方式，算法极易跳出局部极值点。本文在系统驱动能量损耗指标下，提出了采用种群特征进行反馈控制，动态调节CS算法参数，提高算法的全局探测及局部搜索能力。从而实现舵角/翼舵角的最优分配，进一步提高航向控制精度。仿真结果证明了该方法的有效性。

1 舵/翼舵优化分配问题描述

与传统的整体舵相比，舵/翼舵操纵面的增多面临的问题是如何进行控制分配。图1给出了舶舵/翼舵航向控制系统结构图，其中航向调节器、舵/翼舵角度智能分配决策器组成。航向调节器根据航向检测装置得到的航向角计算出所需的艏摇控制力矩，舵/翼舵角度智能分配决策器根据艏摇控制力矩值进行舵角/翼舵角的最优分配，并通过与此时角度传感器检测的角度的差值来驱动舵伺服系统和翼舵伺服系统运动，最终产生相应的回转力矩，实现对船舶航向的精确控制。

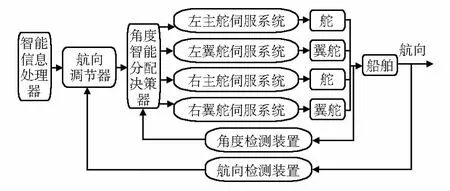
图1 船舶舵/翼舵—航向控制系统结构

2 舵/翼舵角度优化分配规则

设计舵角/翼舵角分配规则，需综合考虑舵角/翼舵角的分配能否提供船舶航向控制所需的扶正力矩、舵/翼舵伺服系统对舵角/翼舵角的限制以及舵/翼舵伺服系统“驱动能量最小”的目标等问题。

1)航向控制艏摇扶正力矩等式约束条件

根据航向控制系统结构图1，给出系统的等式约束条件，即舵/翼舵产生艏摇扶正力矩应等于航向调节器计算得到的控制扶正力矩

Nf(αr(k+1),βr(k+1))=Nψ(k+1)

(1)

式中Nf(αr(k+1),βr(k+1))为舵/翼舵产生的艏摇控制力矩值；Nψ(k+1)为由航向调节器计算得到的艏摇控制力矩值；αr(k+1),βr(k+1)分别为k+1时刻的舵角和翼舵角。

舵/翼舵产生的艏摇控制力矩由下式求得

Nr(αr(k+1),βr(k+1))=-(1+aH)xRPy

(2)

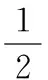
2)舵/翼舵多操纵面不等式约束条件

舵角/翼舵角限位及舵速/翼舵速度的限制

|αr(k+1)|≤αrmax,|βr(k+1)|≤βrmax

(3)

(4)

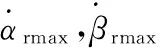
此外水动力试验表明，当αr>27°，βr/αr>1.6时，随着βr/αr的增大,Cyr反而减小，同时考虑到机械结构的物理限制，对舵/翼舵角度进行如下约束

(5)

3)优化目标函数建立

从船舶的驱动能量角度考虑建立系统优化目标函数。在文献[7]的相关研究基础上，将翼舵舵面相对于主舵轴转动的能量损耗加以修正，给出了新的舵/翼舵从αr(k)/βr(k)转至αr(k+1)/βr(k+1)过程中伺服系统能量驱动方程

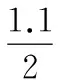
(1.1MJ+1.1Mh)×(αr(k+1)-αr(k))+

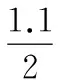
(1.1MJw+1.1Mhw)×(βr(k+1)-βr(k))

(6)

式中MJ,Mh分别为舵速变化时产生的惯性力矩、恢复力矩；MJw,Mhw分别为翼舵的惯性力矩、恢复力矩；Cm(αr,βr)为舵扭矩系数；Cmw(αr,βr)为翼舵扭矩系数；Sp为舵面积；Spw为翼舵面积；bp,bpw分别为水动力作用点距舵/翼舵轴的距离。

4)舵角/翼舵角优化分配规则

当舵型参数确定后，ΔJr(k+1)为αr(k+1)和βr(k+1)的函数，舵角/翼舵角的优化分配规则如下

min ΔJr(k+1)

(7)

3 舵/翼舵角度改进的动态布谷鸟搜索算法优化分配策略

1)CS算法闭环控制

在文献[11]提出的参数闭环控制思想基础上，将CS算法中的种群概念引入闭环系统中，给出了CS算法闭环控制框架，如图2所示。从图中可以看出，该控制框架的核心在于选取合适易得的种群特征以及设计参数调整策略。

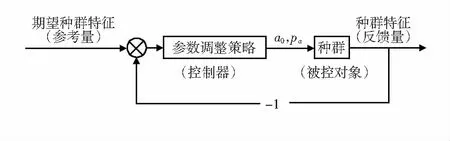
图2 CS算法闭环控制框架

2)种群特征选取

将Lévy Flight视为遗传过程，则获得更优解的个体视为幼年个体，否则为老年个体；将宿主发现过程视为变异过程，则获得更优解的个体视为变异成功个体，否则为变异失败个体，因此可采用幼年个体数与中老年个体数的比值Ra作为反馈信息调整主导Lévy Flight过程的参数α0，采用变异成功个体数与变异失败个体数比值Rm作为反馈信息调整主导宿主发现过程的参数pa。

3)动态调整策略

a.步长控制因子α0调整策略

步长控制因子α0采用幼年个体数与中老年个体数的比值Ra调整。当Ra越大，表明在当前步长控制因子α0下，算法通过Lévy Flight能以较大概率找到更优秀的新解，空间局部搜索性能较好，为提高搜索效率，应适当加大步长以提高种群的探索能力；而当Ra越小时，表明在当前步长下，算法通过Lévy Flight找到更优秀的新解的概率较低，搜索精度较低，空间局部搜索性能不佳，应该适当缩小步长以提高空间的局部搜索能力。采用下面公式调整α0

(8)

注意，极端情况下Ra=1时，表明幼年个体数与中老年个体数相同，种群在当前步长下得到优秀解的概率为50 %，不适于根据当前的反馈信息调整参数α0；而当Ra>1时，幼年个体数比中老年个体数多，找到优秀新解的概率较大，因此加大步长；当Ra<1时找到优秀新解的概率较小，缩小步长，这与前面分析的结果是相符的。

b.发现概率pa调整策略

发现概率pa采用变异成功个体数与变异未成功个体数比值Rm调整。当Rm越大，表明探索新领域的个体能够大概率找到更优秀新解，新领域中优秀的解存在可能性更大，应适当提高发现概率pa，使更多个体探索新领域；当Rm越小，表明新领域中存在优秀解的可能性较小，为了提高效率，可以降低发现概率pa，节省目标函数的计算次数。采用式(9)调整pa

(9)

同理，极端情况下Rm=1时，表明探索新领域的个体成功的概率为50 %，因此这种情况下改变参数pa是不合适的；而当Rm>1时，探索新领域成功率较高，可以提高探索新领域的概率；当Rm<1时，探索新领域成功率较低，为了提高效率，降低探索新领域的概率。此外需要注意的是α0和pa的范围以避免参数过调的情况。

4)约束处理策略

针对CS算法是基于无约束的随机优化算法，因此在求解约束优化问题时首先要进行约束处理技术研究。本文根据文献[13]中提出的基于联赛选择算子的可行性规则来选择个体:

a.如果被选择的两个个体均为可行解，则目标函数值小的解更优；

b.如果被选择的两个个体一个为可行解，一个为不可行解，则可行解更优；

c.如果被选择的两个个体均为不可行解，则约束违反程度低的个体更优。

约束违反度计算公式为

(10)

式中gi(x)为等式约束条件，对应于本文中公式(1)；hi(x)为不等式约束条件，对应于文中公式(3)～式(5)。

5)舵/翼舵角度改进布谷鸟算法优化步骤

算法运行开始前，注意确定各参数的上下限防止参数过调，步骤如下：

a.根据舵/翼舵角度限制，初始化种群，给出初始鸟窝位置，并设置算法终止条件。

b.根据可行性规则式(13)以及舵/翼舵优化分配规则中等式约束条件式(1)、式(2)和不等式约束条件式(3)～式(5)，根据驱动能量消耗指标式(6)计算各个个体的适应度值并排序，找出最优鸟窝位置及其对应的最优适应度值。

c.判断算法是否满足终止条件，若满足，则算法终止；否则，转下一步。

d.对于每个个体，按照Lévy Flight得到新解，如果新解被保留下来，幼年个体数+1，老年个体数-1，计算Ra。

e.生成[0,1]之间的随机数，与pa比较，按照概率决定探索新领域的个体数，记录每个个体变异状态，成功表示为1，未成功表示为0。

f.根据所提出的动态调整策略，即采用式(8)、式(9)计算下一代种群的步长控制因子α0、发现概率pa。

g.根据步骤(2)计算全局最优解，如果不满足终止条件，则重复步骤(3)～步骤(7)。

4 仿真分析

1)在相同的仿真条件下，给出舵/翼舵与普通单体舵的航向控制效果、角度分配情况以及能量损耗情况分析；

2)在相同的仿真条件下，对舵/翼舵角度采用GA、基本CS算法以及本文的IDCS算法进行智能优化分配，对系统能量损耗进行分析。

IDCS算法参数：种群规模N=25，发现概率初值pa=0.25，pa∈[0,1]，步长控制因子初值α0、最小值α0,min和最大值α0,max分别为搜索范围的1/200，1/4 000和1/100，其他参数见文献[7,10]。

本文中船舶的主舵面积为9 m2，翼舵面积为2.25 m2，舵/翼舵角度限制为35°，舵/翼舵速度限制为4°/s，仿真海情为3.8 m，船舶航速为18 kn，图3给出了遭遇浪向角为90°时的艏摇干扰力矩仿真曲线以及不采用舵进行闭环控制时的偏航角曲线，图4、图5分别给出了采用单体舵和舵/翼舵的船舶航向控制系统仿真曲线。表1和表2给出了遭遇浪向角为45°,90°,135°时，采用单体舵和舵/翼舵的航向控制系统仿真统计值。其中，角度的量纲均为(°)，E(·)表示均值，STD(·)表示标准差，η代表舵角饱和率，J代表能耗，J，N为采样次数。仿真中采样时间为0.1 s。

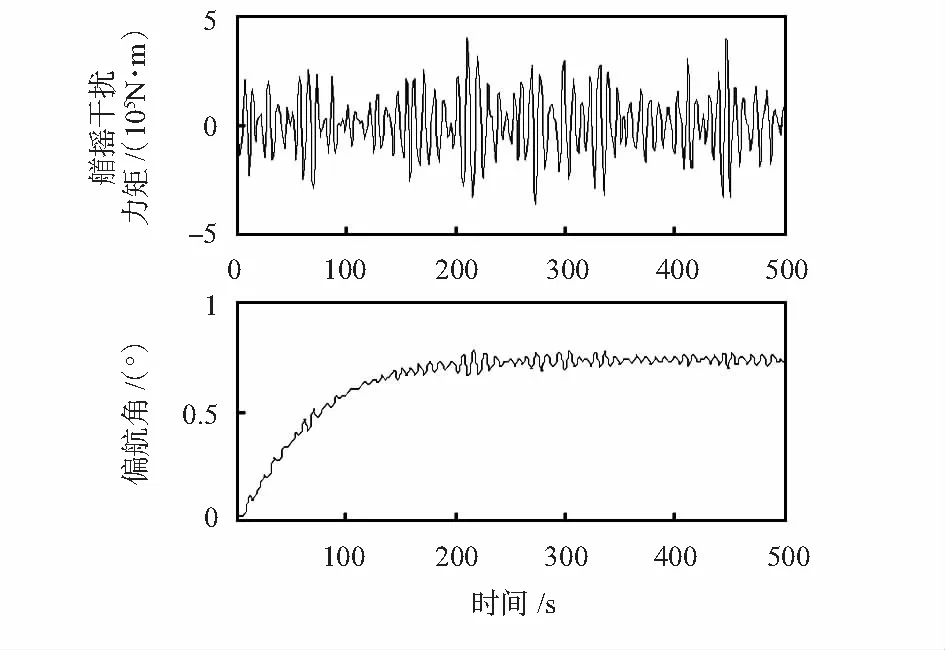
图3 海浪干扰力矩与偏航角仿真曲线(90°)

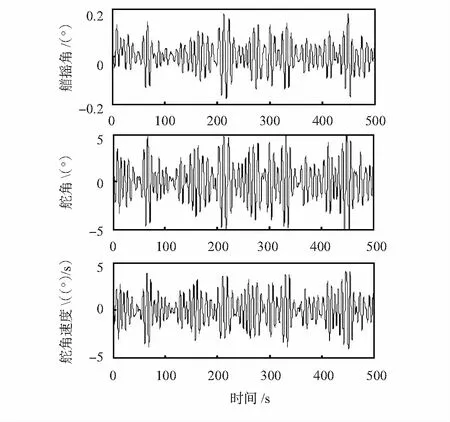
图4 单体舵航向控制系统仿真曲线(90°)

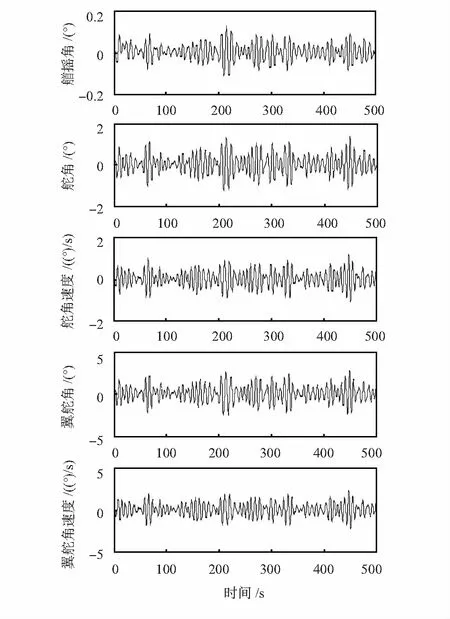
图5 舵/翼舵航向控制系统仿真曲线(90°)

由图3可知，在海浪干扰下，不加入控制时，船舶会偏离给定航向，增加了系统能耗。由图4和图5可知，相同条件下，采用单体舵进行航向控制，主舵需要打较大的角度提供所需的扶正力矩，甚至引起了舵速饱和，从而导致航向控制精度下降，同时单体舵的大幅度转动也增加系统能量损耗；而采用舵/翼舵进行航向控制时，通过本文算法优化合理分配舵/翼舵角度，减小了主舵的运动幅度，主要通过小翼面的翼舵摆动提供所需的航向扶正力矩，舵/翼舵速度也都限制在4°/s以内，因此不仅节省了系统能耗，同时提高了系统航向控制精度。

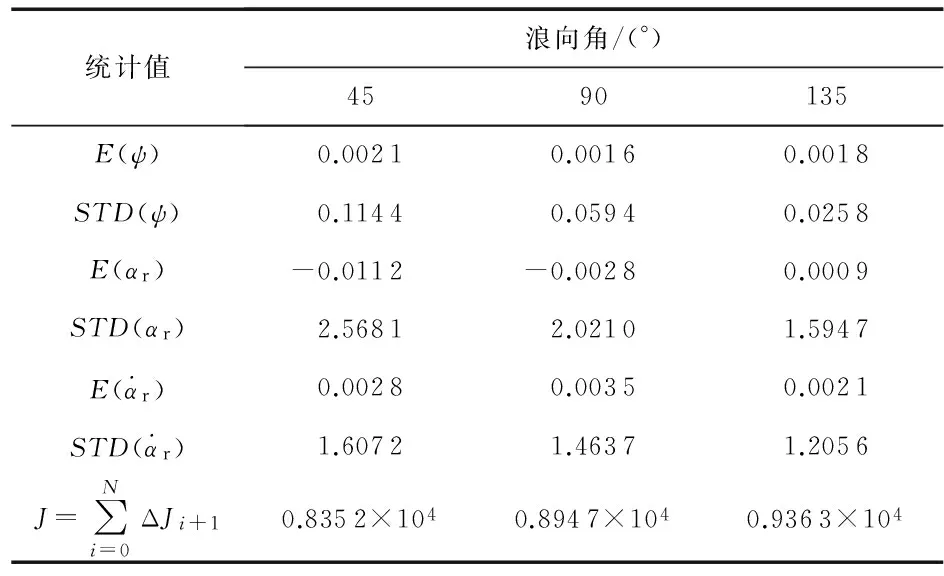
表1 单体舵航向控制系统在不同浪向角下的仿真统计值

对比表1、表2数据可知，在相同浪向角下，采用舵/翼舵比单体舵能够取得更好的航向控制效果，充分利用了翼舵效能，并且能够有效避免主舵角饱和问题，节省了系统能量损耗。而且浪向角不同的情况下，首斜浪时系统能够获得更好的航向控制效果，主要是首斜浪时相对来流速度较大，提高了舵面的升力控制效果。

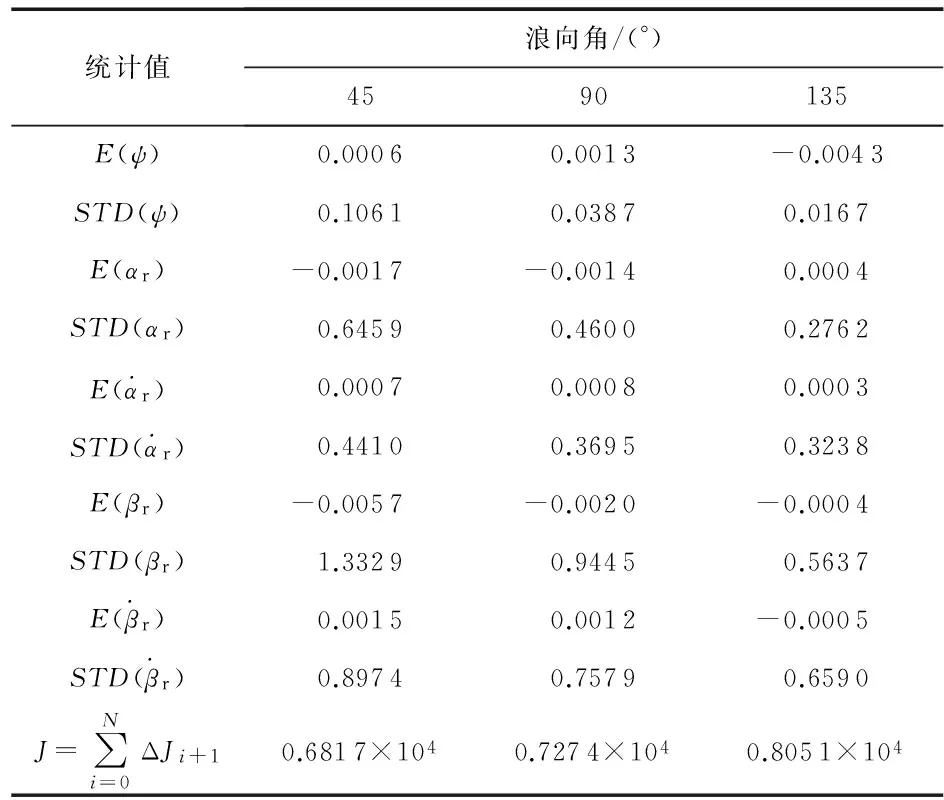
表2 舵/翼舵航向控制系统仿真统计值

图6中给出了遭遇浪向角90°时，采用单体舵进行航向控制的能量损耗曲线以及舵/翼舵分别采用遗传算法、基本CS算法以及本文IDCS算法进行智能优化分配时的能量损耗曲线。可以看出：本文方法能够更加有效地节省驱动能耗。在相同的仿真条件下，随着时间的增加，驱动能量的损耗变大，并且能够获得更小的能量损耗。同时，仿真结果对比也证明了从“驱动能量最小”的角度建立分配规则是合理的。

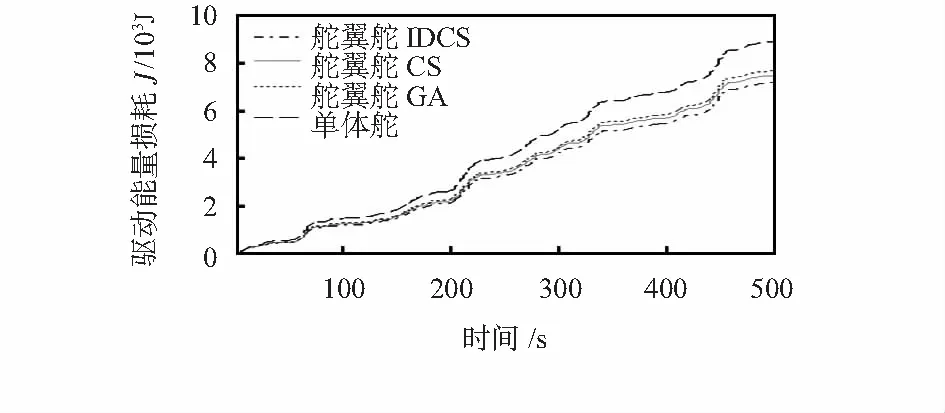
图6 驱动能量损耗曲线

5 结 论

本文针对舵/翼舵角度分配问题及航向保持控制问题，根据航向控制机理，给出了系统控制结构，并修正了舵/翼舵角度分配规则。提出采用改进的动态布谷鸟搜索算法从“驱动能耗最小”角度下进行角度智能优化分配。将种群特征作为反馈引入了算法框架，实现算法参数动态调节，提高了系统寻优过程的全局探测及局部搜索能力；同时根据可行性规则处理约束条件，实现了约束条件下舵角/翼舵角的智能优化分配。仿真结果不仅验证了采用舵/翼舵能够避免单体舵出现的舵速饱和现象，改善航向控制效果并有效降低系统能耗；而且IDCS算法相较于GA和CS算法，在实现舵角/翼舵角分配时能够取得更小的能耗指标，证明了本文提出的舵角/翼舵角分配策略的有效性和工程应用价值。

[1] 徐国平,张显库.船舶自动舵研究综述[J].中国造船,2013,54(2):191-200.

[2] 周丽明,刘 胜.船舶航向保持静态抗饱和控制[J].船舶力学,2011,15(7):757-762.

[3] Li Z,Sun J,Soryeok Oh.Path following for marine surface vessels with rudder and roll constraints:An MPC approach[C]∥Proc of 2009 American Control Conference,2009:3611-3616.

[4] 刘 胜,王宇超,傅荟璇.船舶航向保持变论域模糊—最小二乘支持向量机复合控制[J].控制理论与应用,2011,28(4):485-490.

[5] 马向能,朱小敏,江汉民.新型襟翼舵水动力性能系列试验[J].船舶力学,1999,3(5):15-26.

[6] 丁玲玲,刘 胜.舰船主舵/襟翼舵广义预测联合控制规律研究[J].哈尔滨工程大学学报,2000,21(3):1-6.

[7] Liu Sheng,Fang Liang.Rudder/flap joint intelligent control for ship course system[C]∥Proc of 2007 IEEE International Conference on Mechatronics and Automation,2007:1890-1895.

[8] 黄 胜,任万龙,王 超.基于粒子群算法的水翼剖面多目标优化[J].哈尔滨工程大学学报，2014,35(12):1-7.

[9] 金鸿章,王 帆.低舵速下具有能量优化的舵鳍联合减摇研究[J].兵工学报,2009,30(7):945-950.

[10] Yang X S,Deb S.Cuckoo search via Lévy flights[C]∥Proc of the World Congress on Nature & Biologically Inspired Computing,NABIC’09,2009:210-214.

[11] 张永韡,汪 镭,吴启迪.动态适应布谷鸟搜索算法[J].控制与决策,2014,29 (4):617-622.

[12] Pathak R K,Gopesh A,Dwivedi A C.Age composition,growth rate and age pyramid of an exotic fish species,Cyprinus carpio var communis from the Ganga river at Allahabad,India[J].National Academy Science Letters:India,2011,34(5-6):223-228.

[13] 龙 文,陈 乐.求解约束化工优化问题的混合布谷鸟搜索算法[J].计算机应用,2014,34(2):523-527.

[14] Yang X S,Deb S.Engineering optimization by cuckoo search[J].International Journal of Mathematical Modelling and Numerical Optimisation,2010,1(4):330-343.

[15] Valian E.A cuckoo search algorithm by Lévy flights for solving reliability redundancy allocation problems[J].Engineering Optimization,2013,45(11):1273-1286.

Main/FlaprudderwithIDCSenergyoptimizationforshipcourse-keepingcontrol*

LIU Sheng， SONG Ying-hui， JIA Yun-lu

(CollegeofAutomation,HarbinEngineeringUniversity,Harbin150001,China)

Ship with main/flap rudder which is effective to improve the lift coefficient,also can reduce energy loss of system,but increase of the control surface will bring angle optimization allocation problem.According to the course control mechanism,the main/flap rudder angle optimization allocation rules is established,and an improved dynamic cuckoo search(IDCS)algorithm is proposed to improve the global detect and local search ability,in order to achieve the main/flap rudder angles optimal allocation.The simulation result shows that compare to the common rudder,the main/flap rudder can effectively avoid speed saturation and improve course control effect and reduce system energy loss;also compared to GA and CS algorithm,the main/flap rudder allocation strategy based on IDCS algorithm can achieve smaller energy loss indicators,the effectiveness and practical engineering value of the proposed algorithm is proved.

ship;main/flap rudder; improved dynamic cuckoo search (IDCS); energy optimization; course-keeping control

10.13873/J.1000—9787(2017)11—0070—05

U 661.74; TP 399

A

1000—9787(2017)11—0070—05

2016—03—28

国家自然科学基金资助项目(51079033,51279036)；中央高校基本科研业务费专项资金资助项目 (HEUCFX41305)

刘 胜(1957-)，男，博士，教授，主要从事船舶运动姿态控制、鲁棒控制与应用、先进控制理论方向研究工作。

宋颖慧，通讯作者，E-mail：huijustdoit@126.com。