板形矫正轧辊轧制变形的受力分析与仿真研究

肖艳军, 冯 华, 井 然, 宋海平

(河北工业大学 机械工程学院,天津 300132)

板形矫正轧辊轧制变形的受力分析与仿真研究

肖艳军, 冯 华, 井 然, 宋海平

(河北工业大学 机械工程学院,天津 300132)

文章对目前锂电池极片轧辊利用小辊颈结构减少和控制轧辊挠度变形的方法提出质疑。在建立轧辊参数模型的基础上,首先通过理论分析的方法求解对小辊颈结构施加矫正拉力前、后轧辊的变形挠度大小;然后利用数值模拟的方法对其进行静态模拟仿真,模拟不同工况下轧辊的变形与应力分布;分析了在施加矫正拉力前、后其轧制区的变形分布与数值大小,得出施加拉力产生的最大矫正变形量所占比例不超过原变形量的0.7%。采用理论分析与数值模拟相结合的方法得到的结果证明,通过增加小辊颈结构改善轧辊变形的方法在实施时既增加材料成本又导致机构繁琐,并且不能有效地减少和控制轧辊的挠度变形,因此,增加小辊颈结构施加拉力是没有必要的。该结论可以为极片轧辊的结构设计提供一定的参考。

锂电池极片;板形矫正轧辊;数值模拟;矫正拉力;变形

轧制过程作为锂离子电池极片生产的一个非常重要的工艺环节,直接影响极片的品质。在轧制过程中,轧辊与极片直接接触,产生挠度变形,轧辊变形会对锂电极片的表面精度产生很大的影响,因此减少和控制轧辊的挠度变形十分重要[1-2]。针对该问题目前采取的措施有3种,其中一种是通过轧辊自身的结构抑制轧辊变形[3-4]。根据市场调查可知,现在市场上一种主流轧辊(也称板形矫正轧辊)的结构示意图如图1所示。

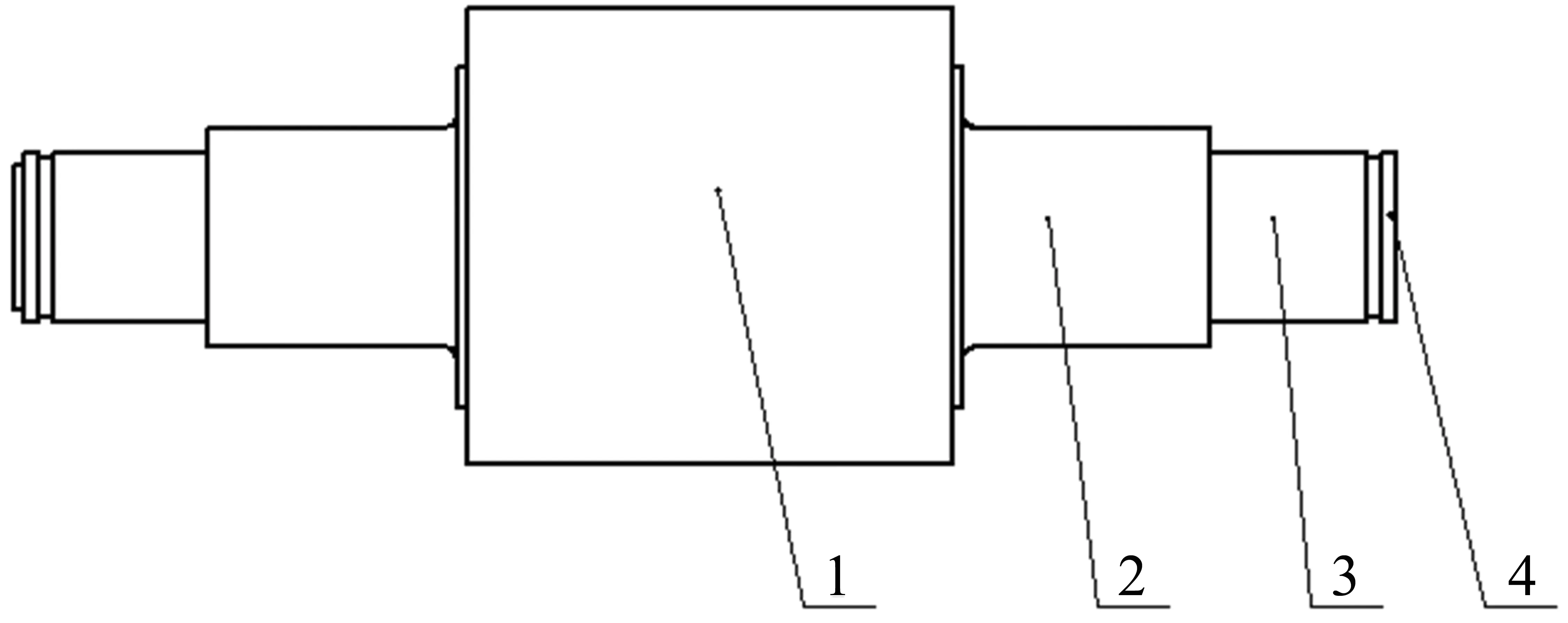
1.辊身 2.大辊颈 3.小辊颈 4.辊头

该轧辊主要增加了小辊颈的结构,其不仅提供消隙作用,更重要的是在小辊颈上施加拉力。从理论角度分析,该拉力可以抵消一部分由轧制力引起的挠度变形,但是抵消的程度并没有相关的研究资料,且该轧辊大大增加了轧辊材料与成本,且施加拉力的装置非常庞大导致机构繁琐,基于上述因素,探究轧辊施加拉力前、后轧制区变形量至关重要。

轧辊可理解为阶梯轴,计算其变形比较复杂,对该变形问题,很多学者进行了理论研究。文献[5]通过引入奇异函数求解了量的挠曲线方程;文献[6]提出了连续分段一体化积分法,可解决复杂载荷下变截面梁弯曲变形问题;文献[7]采用叠加原理的方法分析了多个参考系下梁的挠度,大大简化了问题。

本文首先分析轧辊在受力状态下的变形情况,再对轧辊进行静态模拟仿真,得到不同工况、不同施力条件下轧辊的应力与变形分布,这样既可以真实地反映轧辊受力情况,又可方便地得到不同条件下轧辊的轧制规律[8-10]。

1 轧辊结构与受力分析

1.1 计算对象

本文采用的φ750极片板形矫正轧辊模型如图2所示。该模型采用整体锻造,辊身处进行极片轧制,两侧由185 mm宽的轧机主轴承支撑,小辊颈每侧最靠侧边处安装2个拉力轴承,该轴承既提供拉力也用来消除主轴承间隙,辊头与十字万向联轴器联接传递扭矩。

该极片轧辊模型的主要参数为:辊身直径750 mm,辊身长度800 mm,主轴承宽度185 mm,拉力轴承宽度65 mm,极片宽度400 mm,静态轧制区面积2.4×104mm2。

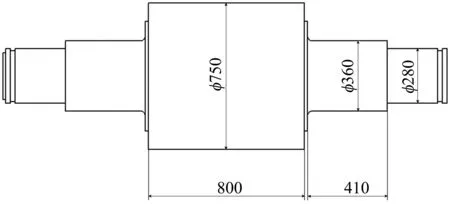
图2 轧辊模型

1.2 轧辊受力分析

本文对轧辊进行静态受力分析。假定轧辊受力为对称分布,在轧制中,轧辊主要受轧制力的作用,左右辊颈受主轴承支撑约束,且拉力轴承对轧辊提供拉力,均匀分布在轧辊上。

将轧辊受力分为不施加拉力和施加拉力2种情况。不施加拉力即轧辊只受轧制力与主轴承支撑而产生变形;施加拉力即拉力轴承提供拉力,且轧辊受到轧制力与主轴承支撑产生变形。轧辊的受力示意图如图3所示。

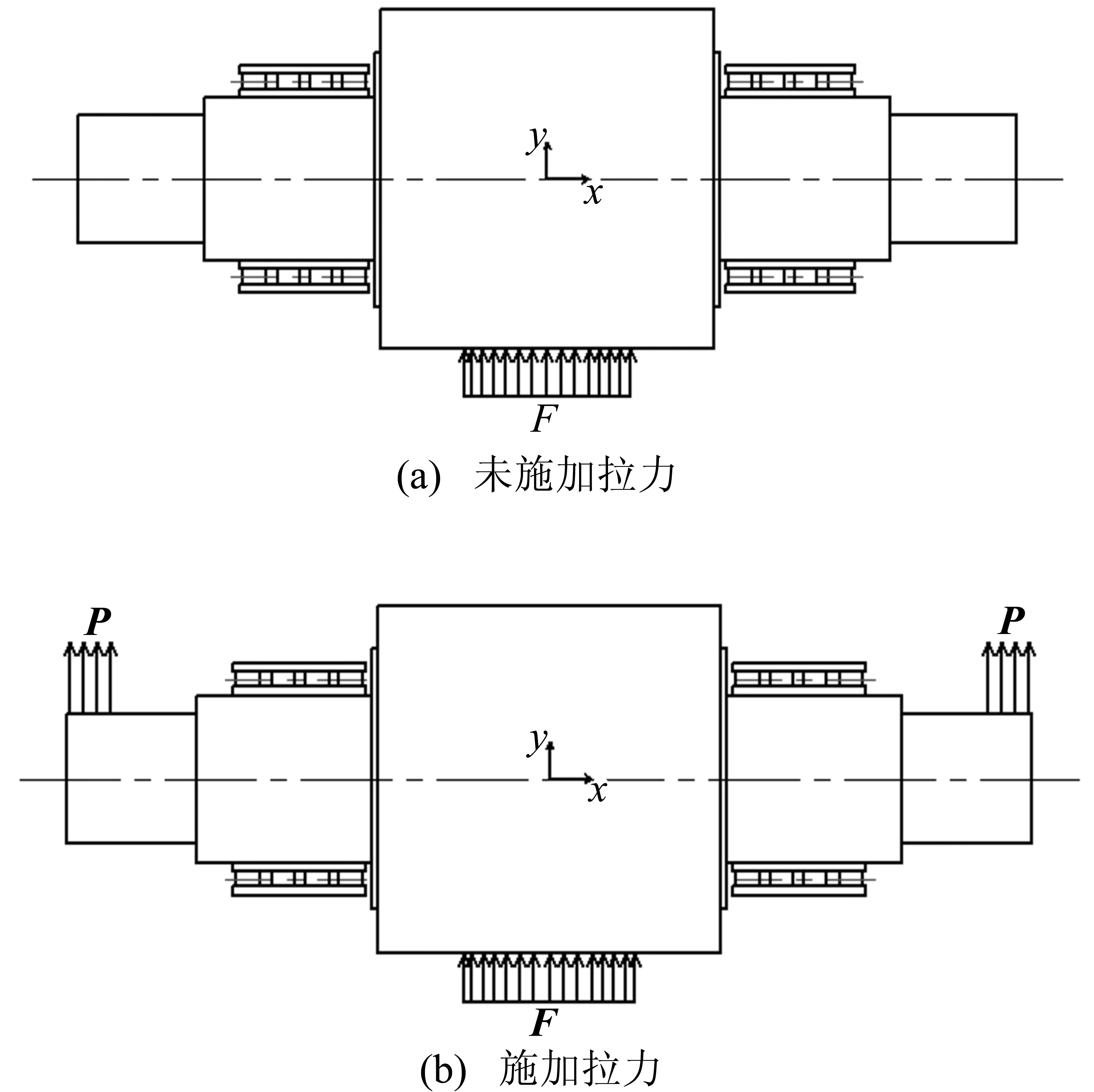
图3 轧辊受力示意图

轧辊所受轧制力一般为500～3 000 kN。为了更准确地分析轧辊在2种受力状态下的变形与应力分布,本文采用工况1(500 kN)、工况2(1 000 kN)、工况3(2 000 kN)、工况4(3 000 kN)4种工况分别对轧辊进行分析。

1.3 轧辊受力变形计算

1.3.1 未施加拉力时的受力模型

轧辊可理解为阶梯轴,通过参考系法利用多个参考系梁的挠度和转角的合成关系,计算轧制区最大变形量,未施加力时的简化受力模型如图4所示。

取3个截面,对应的长度分别为L1、L2、L3,各段的抗弯刚度分别为EI1、EI2、EI3。

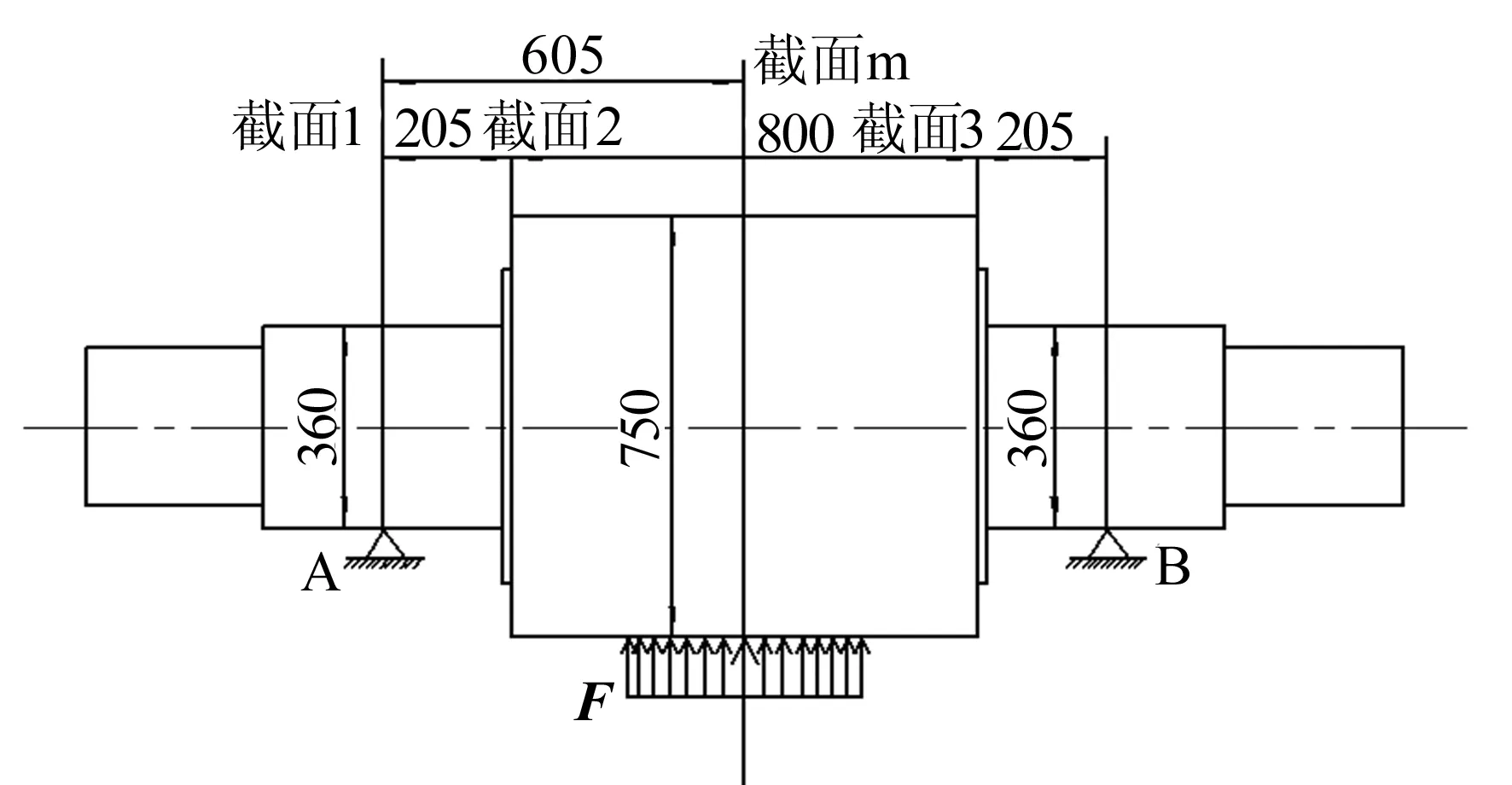
图4 未施加拉力时的受力模型

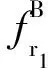
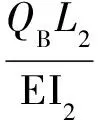
(1)

(2)

因此,截面B相对于动系1总相对挠度为:

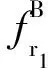
(3)

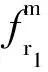
(4)

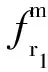
(5)

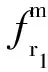
(6)

则有:

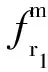
(7)

而动系1对截面m的牵连挠度为:

(8)

则截面m的变形量为:

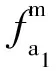
(9)

取轧制力为最大(即轧制力为3 000 kN)时,将数据代入上述公式可得,在未施加拉力的情况下,轧辊轧制区最大变形量约为68.447×10-6m。

1.3.2 施加拉力时的受力模型

建立施加拉力后轧辊的简化受力模型,如图5所示。

取4个截面,对应长度分别为L1、L2、L3、L4,各段的抗弯刚度分别为EI1、EI2、EI3、EI4。

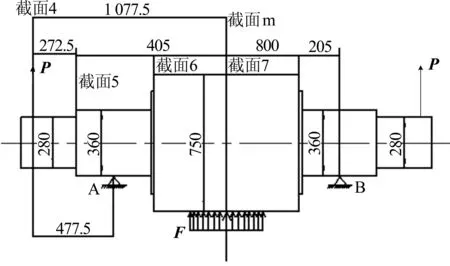
图5 施加拉力时受力模型

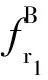
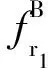
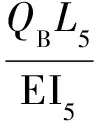
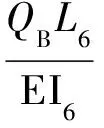
(10)

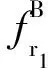
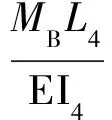
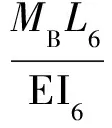
(11)

(12)

(13)

因此截面B相对于动系1总的相对挠度为:

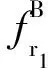
(14)

而牵连挠度为:

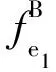
(15)

从而求得转角θ1。

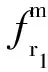
(16)

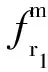
(17)

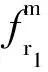
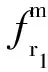
(18)

而动系1对截面m的牵连挠度为:

(19)

则截面m的变形量为:

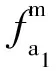
(20)

当轧制力为3 000 kN时,轧辊最大等效应力为68 786 982.25 N,即其强度极限时所需施加的拉力,将数据代入,在施加最大拉力的情况下,轧辊轧制区最大变形量约为67.945×10-6m。

通过上述变形计算,可得当轧制力为3 000 kN时,施加拉力后的最大变形量比施加拉力前最大变形量小0.502×10-6m,即约占原变形量的0.7%。

2 有限元建模与边界条件加载

2.1 有限元模型建立与材料属性

利用Solidworks软件建立板形矫正轧辊的实体模型,对实体模型进行简化处理,将实体模型导入ANSYS中,建立其有限元模型。

进入Material Models中添加材料,轧辊(9Gr2Mo)材料属性[11]如下：弹性模量2.36×105MPa,泊松比0.3,密度7.7×103kg/m3,强度极限620 MPa。本文采用20个节点的Solid186单元生成体网格。

2.2 网格划分

进入MeshTool中,选择Smart Size,设置为5,对轧辊整体进行自由网格划分,设置网格尺寸为30 mm,划分网格后总节点数为108 296,总单元个数为29 737。

2.3 边界条件

对轧辊工作特性进行分析。在对轧辊不施加拉力时,将轧辊的主轴承部分进行位移约束,限制其UX、UY、UZ方向的位移,用压力(Pressure)代替极片在轧辊上的轧制力,垂直于辊面均布施加在轧辊与极片接触区域的节点上；在对轧辊施加拉力时,同理,并在两端拉力轴承处施加拉力,模拟出施加力使得轧辊的最大等效应力达到轧辊材料的强度极限。

3 数值模拟结果分析

3.1 未施加拉力时模拟结果分析

3.1.1 位移变形结果分析

4种工况下,未施加拉力时轧辊的位移变形结果云图如图6所示。

图6 轧辊的位移变形云图

由图6可以看出轧辊在只受到轧制力作用时位移变形分布情况,随着轧制力的增加,轧辊的变形也不断增加,轧辊变形的增加将会影响到极片的横向厚度差,其最大变形均发生在轧辊施加轧制力的中心附近。

选取轧辊辊面上沿轴向均布的16个节点,其包含最大变形值,不同工况下轧辊沿着该直线的变形曲线如图7所示。由图7可知,轧辊在不同工况下变形分布均呈抛物线状,随着轧制力的增大,轧制力的变化值与轧辊位移变形值的改变量成正比。

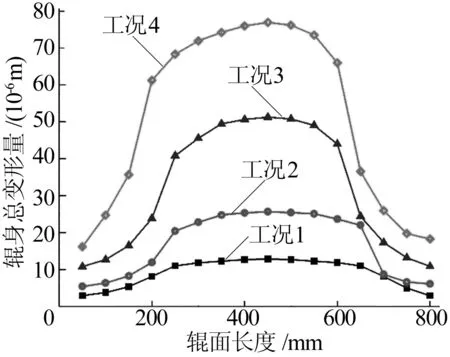
图7 不同工况下变形分布曲线

3.1.2 等效应力结果分析

4种工况下,未施加拉力时轧辊的等效应力结果云图如图8所示。

由图8可知,轧辊在只受轧制力作用时,随着轧制力增加,轧辊的等效应力值也不断增加,轧辊的最大应力值位于轧辊大辊径与辊身交界处,轧辊材料9Gr2Mo的强度极限为620 MPa,选取安全系数为2.5,则许用应力为248 MPa。此时轧辊的最大应力值均小于许用应力,因此,轧制力满足要求。

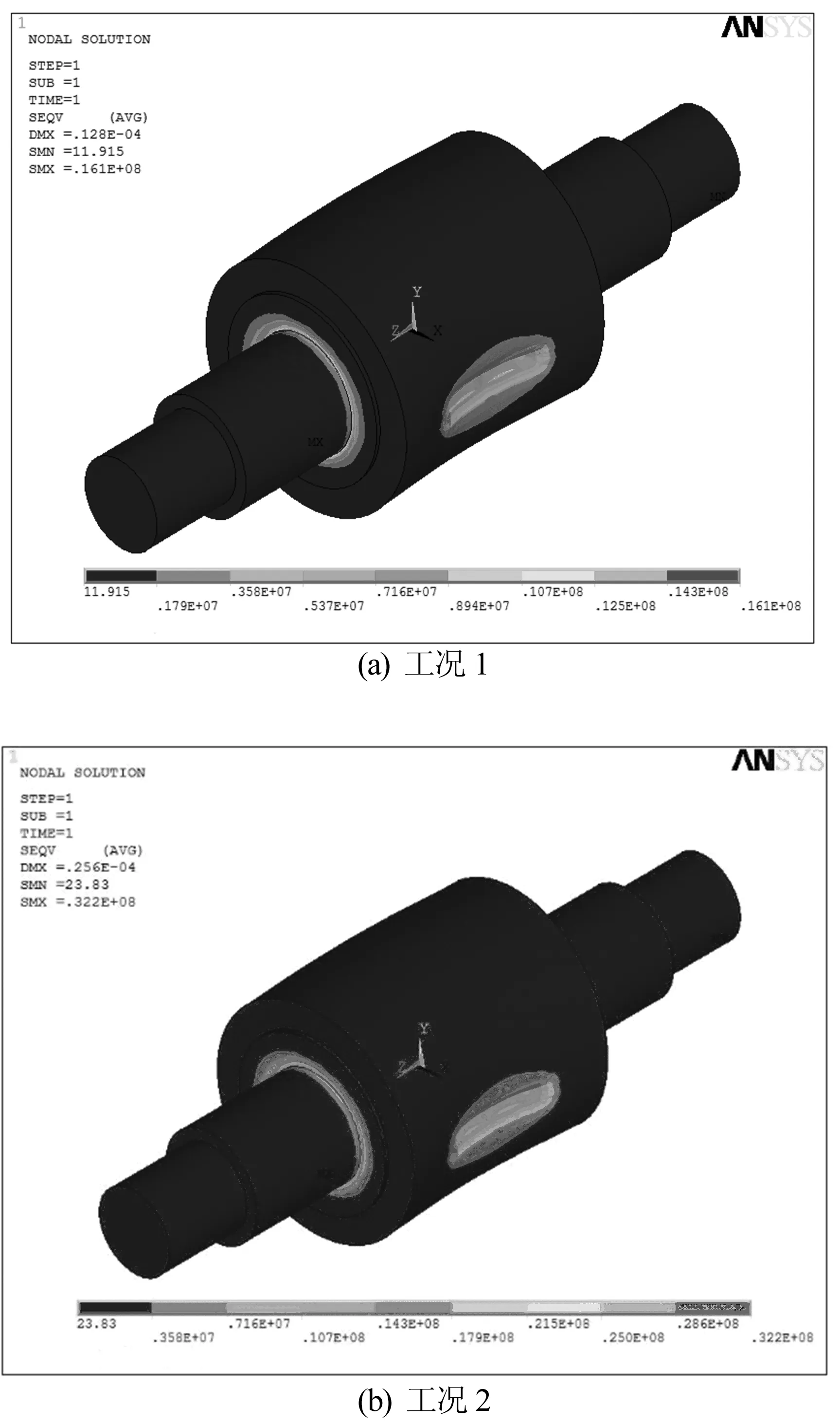
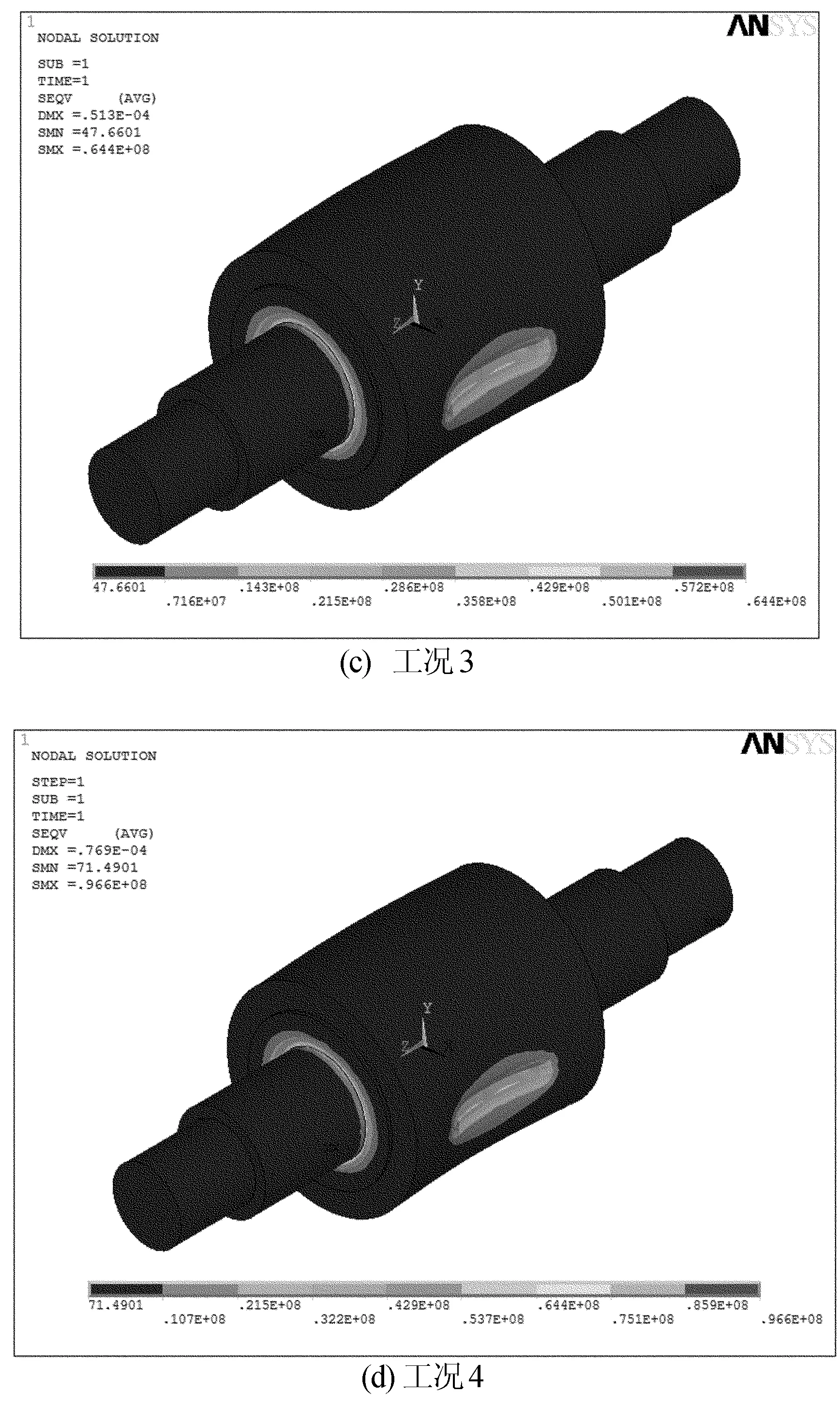
图8 轧辊的等效应力云图

选取轧辊辊面上沿轴向均布的16个节点,其包含最大应力值,不同工况下轧辊沿着该直线的应力分布曲线如图9所示。

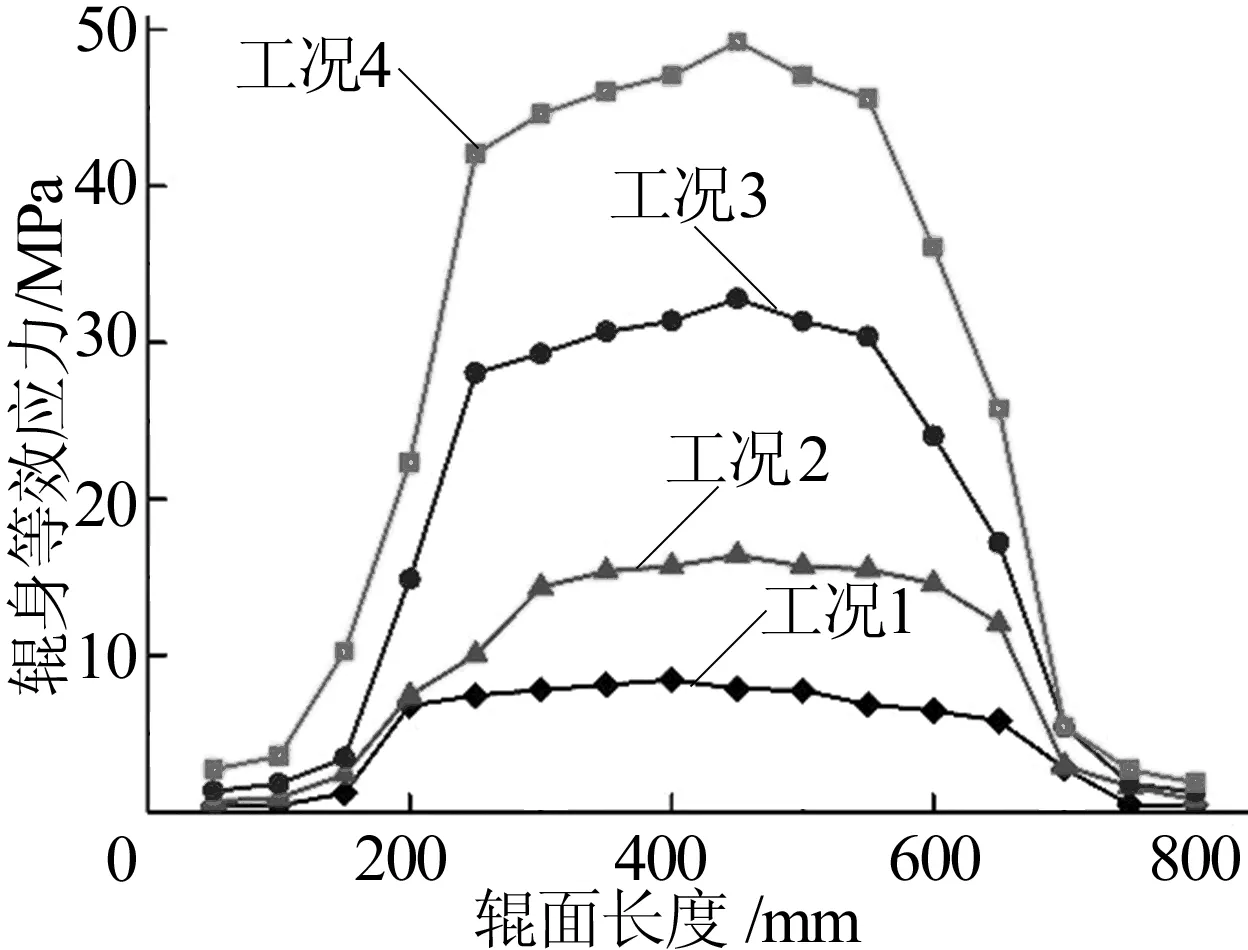
图9 不同工况下应力分布曲线

由图9可知,轧辊沿辊面的应力分布呈抛物线状,在与极片接触区域,不同工况下应力值变化较大,且轧制力的变化值与轧辊应力值的改变量基本成正比。

3.2 未施加拉力时模拟结果分析

为了验证小辊颈上拉力轴承所起的变形矫正作用,通过数值模拟出当轧辊的最大等效应力为强度极限时,拉力轴承上所需施加的拉力的大小,并分析在施加该拉力的情况下,轧辊的位移变形状况,然后与未施加拉力时轧辊的变形数值进行对比。施加拉力后轧辊的等效应力结果云图如图10所示,施加拉力后轧辊的位移变形结果云图如图11所示。

由图10可以看出,轧辊的最大等效应力均为其强度极限值620 MPa,通过仿真模拟可得出,最大等效应力是由所施加拉力引起的,并且所施加拉力与轧辊的最大应力成正比,基于该轧制规律,可快速准确地模拟出最大等效应力为620 MPa时轧辊两侧小辊颈拉力轴承处所需施加的拉力值。

由图11可知,当轧辊的最大等效应力为其强度极限时轧辊的位移变形情况,此时轧辊的最大变形发生在轧辊两端,且轧辊的最大变形量均为571×10-6m,因此该最大变形值主要由轧辊两端施加的拉力产生。为了验证所施加拉力对轧辊在轧制区域变形情况的矫正作用,选取16个节点绘制曲线,4种工况下轧辊2种受力情况下的变形分布对比曲线如图12所示。

由图12可以看出,4种工况下轧辊辊身变形情况均呈抛物线状分布,在轧制区域施加拉力前后变形值变化不明显,由此可以看出其矫正作用不明显。将轧辊未施加拉力时轧制区的最大变形值与施加拉力后的最大变形值进行对比,见表1所列。

随着轧制力的增大,施加拉力时在轧制区产生的最大变形量与未施加拉力时的差值也越大,但其所占总变形的比例却越来越小,即对轧辊的变形产生的矫正作用越来越差,在矫正作用最明显的工况下,施加拉力产生的变形改变量只占未施加拉力时产生的变形量的0.7%以下,所占比例非常小,而且此时最大等效应力为轧辊的强度极限,若轧辊正常工作,最大等效应力在轧辊许用应力范围内时,轧辊因轧制力而产生的变形的矫正作用更是微乎其微。因此可以得出，板形矫正轧辊的小辊颈部分施加拉力是没有必要的,其增加轧辊的长度并将拉力轴承安装在最侧边并没有起到矫正轧辊变形的作用。

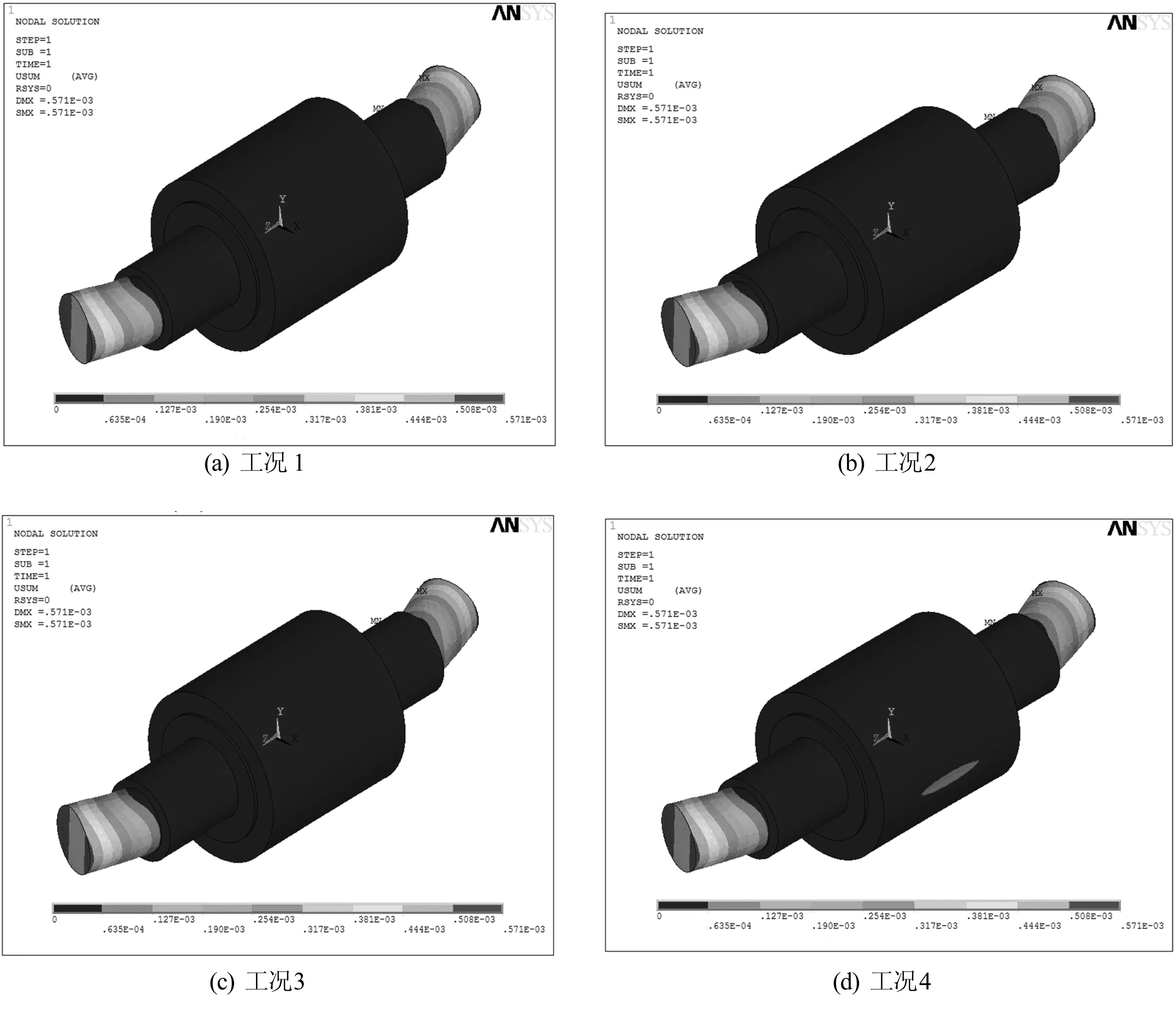
图10 轧辊的等效应力结果云图

图11 轧辊的位移变形结果云图

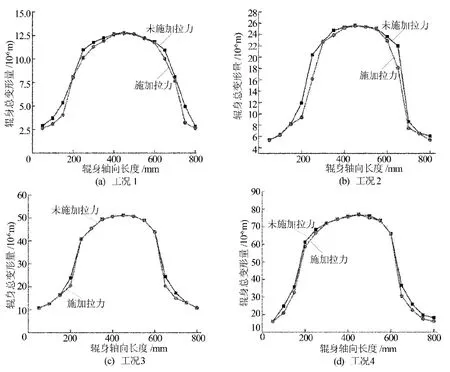
图12 轧辊的变形分布对比曲线

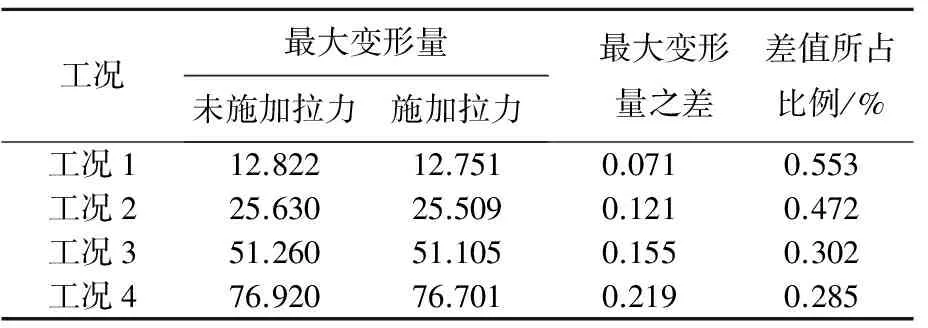
表1 不同工况下轧制区变形矫正情况 10-6m

4 结 论

本文对市场上一种板形矫正轧辊的轧制规律与矫正功能进行研究,得出了如下结论:

(1) 未施加拉力时,轧辊最大应力值位于辊身与大辊径的连接处,且轧制力的变化值与轧辊变形值和应力值的改变量均成正比。

(2) 通过数值模拟仿真得出所施加拉力与轧辊的最大应力成正比,从而可快速准确地模拟出最大等效应力为一定值下的轧辊两侧小辊颈拉力轴承处所需施加的拉力值。

(3) 通过理论计算和仿真模拟对轧辊施加拉力前后轧制区的变形量对比分析,得到板形矫正轧辊既需要增加材料成本又导致机构繁琐的结论,因此可将该结构去除。

[1] 王永洲.电池极片轧机轧辊有限元分析[D].天津: 天津大学,2013.

[2] 龚殿尧,徐建忠,袁方成.四辊轧机不对称刚度条件下轧辊弹性变形的研究[J].东北大学学报(自然科学版),2012,33(11):1586-1590.

[3] 王国栋.板形控制和板形理论[M].北京: 冶金工业出版社,1986.

[4] JIANG Z Y,TIEU A K,ZHANG X M,et al.Finite element simulation of cold rolling of thin strip[J].Journal of Materials Processing Technology,2003,140(1/2/3):542-547.

[5] 冯秋力.组合阶梯轴弯曲变形的拉普拉斯变换计算法[J].长沙电力学院学报(自然科学版),1997,12(2):179-182.

[6] 李银山,官云龙,李彤,等.求解变截面梁变形的快速解析法[J].工程力学,2015,32(6):116-121.

[7] 盛冬发,周沈旺,张宁.变截面轴的变形计算[J].佳木斯大学学报,2010,28(6):853-857.

[8] PARK J J.Numerical analysis of twin-roll casting to fabricate a laminated sheet from melts[J].International Journal of Heat & Mass Transfer,2016,100:590-598.

[9] WISSAM K,FEAN C.Modelling and simulation of mechanical transmission in roller-screw electromechanical actuators[J].Aircraft Engineering and Aerospace Technology,2009,81(4):288-298.

[10] 申潞潞,曹晓卿,刘文拯.镁铝爆炸复合板界面轧制变形行为的数值模拟[J].热加工工艺,2016,45(1):96-100.

[11] 《机械工程材料性能数据手册》编委会.机械工程材料性能数据手册[M].北京: 机械工业出版社.1994.

Forceanalysisandnumericalsimulationresearchofrollingdeformationofshapecorrectionroll

XIAO Yanjun, FENG Hua, JING Ran, SONG Haiping

(School of Mechanical Engineering, Hebei University of Technology, Tianjin 300132, China)

In this paper, the method of reducing and controlling the deformation of the roller using the small roll neck of the pole piece of lithium battery is challenged. Firstly, by the method of theoretical analysis, the roll parameters model is established, and the deformation and the deflection of the roller before and after the application of orthodontic force to the small roll neck are solved. Secondly, ANSYS, a commercial finite element(FE) software code is used to simulate deformation and stress distribution of roll under different working conditions, then the deformation distribution and numerical size of rolling zone before and after the application of orthodontic force are analyzed. It is found that the maximum correct deformation of the applied force is not more than 0.7% of the original deformation. Through the combination of theoretical analysis method and numerical simulation method, it is shown that the small roll neck increases the material cost, causes the complication of the structure, and it can not effectively reduce and control the roll deflection deformation. Therefore, it is not necessary to increase small roll neck structure and it can be removed. The conclusion can provide a reference for the structural design of pole piece roll.

lithium battery pole piece; shape correction roll; numerical simulation; orthodontic force; deformation

2016-07-21；

2016-09-09

国家自然科学基金资助项目(51305124);天津市科技计划资助项目(15JCTPJC62400)

肖艳军(1976-),男,河北沧州人,博士,河北工业大学副教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.10.004

TG335.5

A

1003-5060(2017)10-1312-08

(责任编辑 胡亚敏)