考虑制造商风险规避的闭环供应链回收渠道决策研究

李晨++孙浩

摘 要：研究了制造商的再制造成本风险规避度对闭环供应链回收渠道选择的影响，利用均值—方差理论建立了制造商回收、零售商回收和第三方回收的闭环供应链模型，分别比较和分析了三种渠道的最优回收率、最优销售价格、制造商的最优期望效用以及零售商的最优期望利润。研究表明当制造商的风险规避程度处于相对较低的水平时，零售商回收的效率最高，制造商回收时次之，第三方回收时最低；相反，当再制造成本波动较大且制造商的风险规避程度较高时，零售商回收的系统总利润反而最低。制造商的风险态度和系统的不确定性主要影响零售商的利益，渠道成员应加强信息共享和建立有效的风险共担机制来保证供应链的平稳运行。

关键词：闭环供应链；回收渠道；风险规避；均值—方差

中图分类号：F713.2 文献标识码：A

Abstract： This paper considers the effects of manufacturer's risk aversion degree for uncertain remanufacturing cost on collection channel selection of closed-loop supply chains. Three models including manufacturer-collection， retailer-collection and third-party-collection are built by mean-variance theory. The optimal collection rates， the optimal retail prices， the optimal utilities of manufacturer and the optimal expected profits of retailer under three collection channels are compared and analyzed， respectively. The study has shown that when the degree of the manufacturer's risk aversion is in a relatively lower level， the system efficiency of retailer-collection is the highest； the next is manufacturer-collection and third-party-collection last； on the contrary， when the variability of remanufacturing cost is larger and the degree of the manufacturer's risk aversion is higher， the system efficiency of retailer-collection is the lowest. The risk attitude of the manufacturer and system uncertainty primarily influence the profit of retailer. The channel members should strength information sharing and set up efficient risk-pooling mechanism to ensure that the supply chain operates steadily.

Key words： closed-loop supply chains； collection channels； risk aversion； mean-variance

0 引 言

再制造及閉环供应链管理是近二十年来工业界与企业界共同关注的焦点，世界上许多知名的制造型企业（如IBM、苹果、宝马等）均通过再制造获取了巨额收益。然而，再制造的引入使得企业的生产、库存、定价与成员协作等运营决策更加复杂，因此其也成为学术界所关注的热点议题。在闭环供应链的产品定价策略与回收渠道选择方面，学者们从不同的市场结构、权力结构、新制造产品和再制造产品的定价模式（统一定价或差异定价）以及市场需求环境（确定需求或随机需求）等视角对其展开了深入的研究，并取得了众多阶段性成果[1-6]。但以上文献存在的局限性在于：即使在随机环境下也均以渠道成员风险中性为前提，以期望利润为优化目标。但众所周知，由于废旧产品产生的时间、地点、数量和质量具有高度的不确定性，导致在闭环供应链中决策者面临的风险比传统供应链更大，因而在相关研究中考虑决策者的风险态度是十分必要的。

针对以上问题，文献[7-16]采用金融理论的风险度量工具对以往模型进行拓展，研究了具有风险规避者的闭环供应链定价策略和协调机制。史成东等[7-10]和高文军等[11]分别运用在险值（Value at Risk， VaR）理论和条件在险值（Conditional Value at Risk， CVaR）理论探讨了在风险中性的制造商与具有下行风险特性（Downside-Risk）的零售商所组成的两级闭环供应链中，零售商回收、第三方回收、竞争的双第三方回收等渠道下闭环供应链的风险控制策略和利润协调机制。陈宇科等[12]为克服CVaR的局限性，研究了基于均值-CVaR的闭环供应链协调机制。史成东等[13]和刘秋生等[14]则分别借用前景理论（Prospect Theory， PT）设计了协调两级闭环供应链的收益共享和批量折扣契约以及回购和盈利—亏损共担契约。曹晓刚等[15]在前景理论框架下研究了具有风险规避零售商的闭环供应链网络均衡。肖复东等[16]利用均值方差（Mean Variance， MV）理论分析了零售商不同的需求风险规避度对三种回收渠道模式下的闭环供应链的影响。endprint

文献[7-16]均在制造商风险中性、下游零售商或第三方风险规避的情形下展开研究，主要原因在于零售商（回收商）是Stackelberg主从博弈的被动方，他们比制造商更容易害怕风险。但就我国目前的情况而言，由于再制造工程的发展时间较短，再制造技术尚不够成熟，外加废旧产品的质量参差不齐，导致再制造的成本存在较大的不确定性[17]，从而直接影响到企业实施再制造的收益。所以在闭环供应链决策模型中充分考虑制造商的风险态度具有较大的现实意义。与以往文献不同，本文将针对由单一风险规避制造商与单一风险中性零售商或第三方所组成的闭环供应链，运用均值方差方法探讨和比较三种不同回收渠道下闭环供应链的定价策略、回收率和系统效益，以期为我国企业实施再制造提供理论依据和决策支持。

3 算例分析

本节首先计算当再制造成本标准差σ=8时，三种回收渠道下闭环供应链成员的决策变量利润随风险规避系数λ的变动趋势，然后通过灵敏度分析σ的變动对最优解的影响，其他参数取值分别为a=20， b=0.6， c■=30， c■■=20。

表1表明：在制造商回收渠道下，随着风险规避因子λ的逐渐变大，废旧产品回收率递减，产品零售价格递增，制造商效用、零售商期望利润和系统总利润均随λ的变大而变小。

表2表明：在零售商回收渠道下，随着风险规避因子λ的逐渐变大，废旧产品回收率递减，产品零售价格递增，制造商效用、零售商期望利润和系统总利润均随λ的变大而变小。另外，此时的废品回购价格B并不随λ的增加而变化，仍然维持B

=Δ的最优取值，即无论制造商的风险态度如何，其最优选择均是将再制造的节约成本Δ全部转移给零售商来刺激其提高产品的订购量，进而增加制造商自身的利润，该结论与Savaskan[1]风险中性的结论完全相同。

表3表明：在第三方回收渠道下，随着风险规避因子λ的逐渐变大，废旧产品回收率递减，产品零售价格递增，制造商效用、零售商期望利润、第三方期望利润和系统总利润均随λ的变大而变小。另外，废旧产品的回购价格B随λ的增加而减小，表明随着制造商越来越害怕风险，其对第三方从事回收的激励程度降低，其本身从事再制造的积极性也降低。而与之不同的是：在风险中性情形下，无论其它参数取值如何，回购价格恒等于Δ/2[1，20]。

另外，综合表1至表3分析，无论制造商的风险规避系数如何，在三种回收渠道下，零售商回收时的回收率最高，制造商回收时次之，第三方回收时最低；零售商回收时的产品售价最低、销售量最多；第三方回收时的产品售价最高、销售量最少。以上结论与Savaskan[1]完全相同。

在相同的风险规避系数条件下，零售商回收时的制造商利润最高，制造商自身回收时次之，第三方回收时的制造商利润最低；制造商回收时的零售商利润最高，第三方回收时的零售商利润次之，零售商同时负责销售和回收时其利润最低；当风险规避系数处于中低水平（如小于0.6）时，零售商回收时的系统总利润最高，制造商回收时次之，第三方最低；而当风险规避系数较高（如大于0.8）时，制造商回收时的系统总利润最高；特别地，当风险规避系数为1时，零售商回收的系统总利润已低于第三方回收时。

综合以上数据分析说明：制造商的风险态度主要影响零售商，零售商的利润随风险因子的提高下降最为显著，原因在于作为Stackelberg博弈的主动方，制造商可以通过有效的上层决策来保证自身的利益和影响零售商的决策；而零售商作为博弈的被动方，只能承受利益的损失，尤其当其同时负责产品销售和回收时。从另一个角度来说，当制造商的风险规避程度不是特别高时，零售商回收对于制造商和系统总利润是有益的；但对于零售商而言，尽管制造商已提供最高的回购费用B=10，其仍不具备参与逆向回收的积极性。

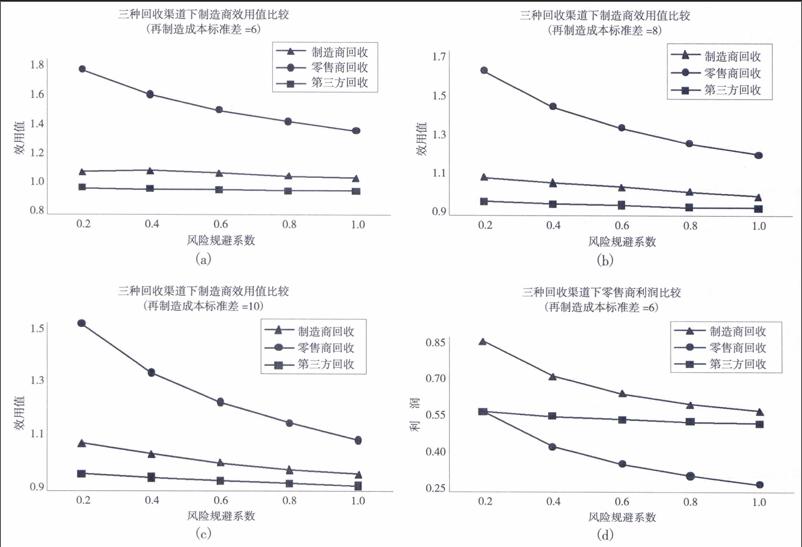
以下考查再制造成本标准差σ的变动对三种回收渠道下制造商效用、零售商利润和系统总利润的影响，分别取σ为6、8和10，具体结果如图1所示。

图1中（a）～（c）给出了再制造标准差对制造商效用的影响，可知在σ=6，8，10三种情形下，均是零售商回收时的制造商利润最高，制造商本身回收时次之，第三方回收时的利润最低；图1中（d）～（f）给出了再制造标准差对零售商期望利润的影响，均是制造商回收时的零售商利润最高，第三方回收时次之，零售商同时负责销售和回收时最低，这同样表明系统的不确定性主要影响零售商的利益。另外，随着风险规避因子的增加，制造商回收和第三方回收两种情形下的差异逐渐减小。图1中（g）～（i）给出了再制造标准差对系统总利润的影响，当σ=6时，零售商回收时的系统总利润最高，制造商回收时次之，第三方回收时最低。但随着再制造标准差的增加，零售商回收时的系统总利润迅速下降，特别当制造商的风险规避因子较大时，其系统效益在三种回收渠道下最低，这主要在于零售商的期望利润随着再制造成本波动和制造商风险规避态度的增加而显著减少，从而造成了系统效益的严重损失。

4 结 论

根据我国企业实施回收再制造的实际情况，假设再制造成本的不确定性导致制造商成为风险规避者，在此基础上建立了制造商回收、零售商回收和第三方回收三种回收渠道下的闭环供应链决策模型，进而结合算例仿真分析了制造商的风险态度和再制造成本的波动对闭环供应链决策的影响，研究结果表明制造商的风险态度和系统的不确定性主要影响零售商的利益，渠道成员应加强信息共享和建立有效的风险共担机制来保证闭环供应链的稳定运行，如在满足参与者激励相容约束和个人理性约束的前提下，制造商与零售商签订收益共享[16]或二部定价[15]等契约。另外，本文的研究可拓展至制造商和零售商均为风险规避者的情形。

参考文献：

[1] Savaskan R C， Bhattacharya S， Wassenhove L N V. Closed-loop supply chain models with product remanufacturing[J]. Management Science， 2004，50（2）：239-252.endprint

[2] Savaskan R C， Wassenhove L N V. Reverse Channel Design： The Case of Competing Retailers[J]. Management （上接第137頁） Science， 2006，52（1）：1-14.

[3] 王文宾，达庆利，聂锐. 考虑渠道权力结构的闭环供应链定价与协调[J]. 中国管理科学，2011，19（5）：29-36.

[4] 王玉燕，申亮. 基于消费者需求差异和渠道权力结构差异的MT-CLSC定价、效率与协调研究[J]. 中国管理科学，2014，22（6）：34-42.

[5] 易余胤，梁家密. 不确定需求下具奖惩机制的闭环供应链模型[J]. 计算机集成制造系统，2012，18（9）：2040-2051.

[6] 洪宪培，王宗军，赵丹. 闭环供应链定价模型与回收渠道选择决策[J]. 管理学报，2012，9（12）：1848-1855.

[7] 史成东，陈菊红，钟麦英. Downside-Risk测度下闭环供应链风险控制和利润分配机制研究[J]. 控制与决策，2009，24（11）：1693-1696，1701.

[8] 史成东，陈菊红，邢同卫，等. 第三方负责回收的Downside-Risk闭环供应链协调性研究[J]. 运筹与管理，2011，20（4）：39

-47，57.

[9] 史成东，闫秀霞，张正民，等. Downside-Risk测度的双第三方回收再制造闭环供应链[J]. 管理学报，2014，11（10）：1520-1527.

[10] 史成东，闫秀霞，闫厚强，等. Loss-averse 测度下考虑政府补贴的双第三方回收再制造闭环供应链[J]. 中国管理科学，2015，23（7）：152-158.

[11] 高文军，陈菊红. 基于CVaR的闭环供应链优化与协调决策研究[J]. 控制与决策，2011，26（4）：489-494，500.

[12] 陈宇科，熊龙，董景荣. 基于均值-CVaR的闭环供应链协调机制[J]. 中国管理科学，2017，25（2）：68-77.

[13] 史成东，陈菊红，郭福利，等. Loss-averse闭环供应链协调[J]. 系统工程理论与实践，2011，31（9）：1668-1673.

[14] 刘秋生，杜潇婕. 具有损失厌恶零售商的闭环供应链协调研究[J]. 商业研究，2011（11）：107-114.

[15] 曹晓刚，郑本荣，夏火松，等. 具有风险规避型零售商的闭环供应链网络均衡分析[J]. 控制与决策，2014，29（4）：659-665.

[16] 肖复东，聂佳佳，赵冬梅. 考虑零售商风险规避的闭环供应链回收策略研究[J]. 工业工程与管理，2011，16（5）：61-67，72.

[17] Robotis A， Boyaci T， Verter V. Investing in reusability of products of uncertain remanufacturing cost： the role of inspection capabilities[J]. International Journal of Production Economics， 2012，140（1）：385-395.

[18] Agrawal V， Seshadri S. Risk intermediation in supply chains[J]. IIE Transactions， 2000，32（9）：819-831.

[19] Tsay A A. Risk sensitivity in distribution channel partnerships： Implications for manufacturer return policies[J]. Journal of Retailing， 2002，7（8）：147-160.

[20] 李新军，林欣怡，达庆利. 闭环供应链的收入共享契约[J]. 东南大学学报（自然科学版），2008，35（3）：535-539.endprint