城市通勤车辆合乘网络模型
2017-11-22程龙何胜学陈经纬
程龙++何胜学++陈经纬


摘 要:针对城市早晚高峰交通拥堵问题,提出了一种通勤车辆的合乘网络模型。新模型充分利用了通勤出行时间与起讫点位置相对比较集中的特点,并考虑了市民通勤出行的不同需求,因此不仅可以方便通勤者高峰时段的出行,而且有利于缓解城市道路交通压力。模型的求解首先利用二分图匹配实现司机乘客的匹配过程,确定可行的司乘匹配集合;然后分别计算各匹配的实际缩减运行距离和总的合乘參与人数;最后使用分层求解的方法确定参与人数限制条件下的最佳合乘匹配。通过算例验证了模型的可行性和有效性,由数值分析可知:合理的通勤合乘有利于减少车辆总的行驶距离;合乘点的引入提高了司机乘客的匹配率和模型的优化效果。
关键词:城市交通;合乘网络;二分图匹配;高峰时段通勤;合乘点
中图分类号:U492.4 文献标识码:A
Abstract: To lighten the congestion during the rushing hours, this paper presented a commuting ride-sharing network model. Making use of the feature of the centralized commuting times and congregated origin-destination locations and taking into account the different demands of commuting, the new model not only facilitates the rush hour commuting, but also relieves the traffic pressure. To solve the model, the paper first used the bipartite matching to realize the process of drivers and passengers matching so as to determine the feasible matching set. Then this study computed the actual reduced travel distance of every feasible matching and the total number of the ride-sharing persons, respectively. At last this study used the hierarchy method to determine the optimal matching set limited to the total number of participated persons. The numerical example verified the feasibility and effectiveness of the new model. The numerical analysis shows that the rational ride-sharing matching can reduce the total travel distance and the introduction of the meeting points can increase the matching ratio of ride-sharing and strengthen the optimized effect of the new model.
Key words: urban traffic; ride-sharing system; bipartite matching; rush hour commute; meeting points
0 引 言
随着我国城镇化的快速发展,城市的机动车保有量迅速增加。同时多数城市的交通基础设施建设或设计不能满足日益增长的城市交通需求,造成了因为交通供需不平衡引起的城市交通问题,在城市早晚高峰时段表现尤其明显。而在处理城市交通问题时机动车合乘可以有效减少城市路网中机动车需求。因为机动车合乘在满足司机自身出行需求的同时也满足了合乘者的出行需求,即在不增加路网机动车数量的同时解决了更多的交通出行需求。
对于机动车合乘国内外已经进行了大量的研究。Cordeau等提出DARP问题[1](Dial-a-Ride Problem),其他学者针对该问题提出了不同的算法[2]。国内学者机动车合乘研究对象大多是出租车,对合乘调度、合乘路径、合乘费率等方向都进行了研究[3-5]。不仅如此,国外发达国家已经对机动车合乘进行了实施和推广。美国在一些快速路上推行高乘载(HOV-high occupancy vehicle)车道,即车辆中需要乘坐二人或多人才可在HOV车道上行驶。国外如Uber等公司也进入国内网约车市场。这些软件的推广一定程度上使居民出行更便利,但对整个城市路网中机动车数量的减少影响不大。因为这些软件雇佣车主的出行行为大多以盈利为目的,因此相关车辆的行驶对路网来说就成为新增的交通量,并没有起到减少城市路网机动车数量减缓城市交通压力的作用。
城市通勤的时间段较集中,出行起讫点较集中且通勤时间段内居民出行数量多,因此易于实现合乘。针对城市上下班通勤车辆合乘问题,本文主要从如下几个方面进行了分析研究:(1)基于城市通勤车辆合乘的可行性,建立对应的合乘优化模型;(2)通过二分图匹配实现对合乘过程的描述;(3)通过改变合乘点选取范围,分析合乘点数量对合乘模型优化结果的影响。
2 算 例
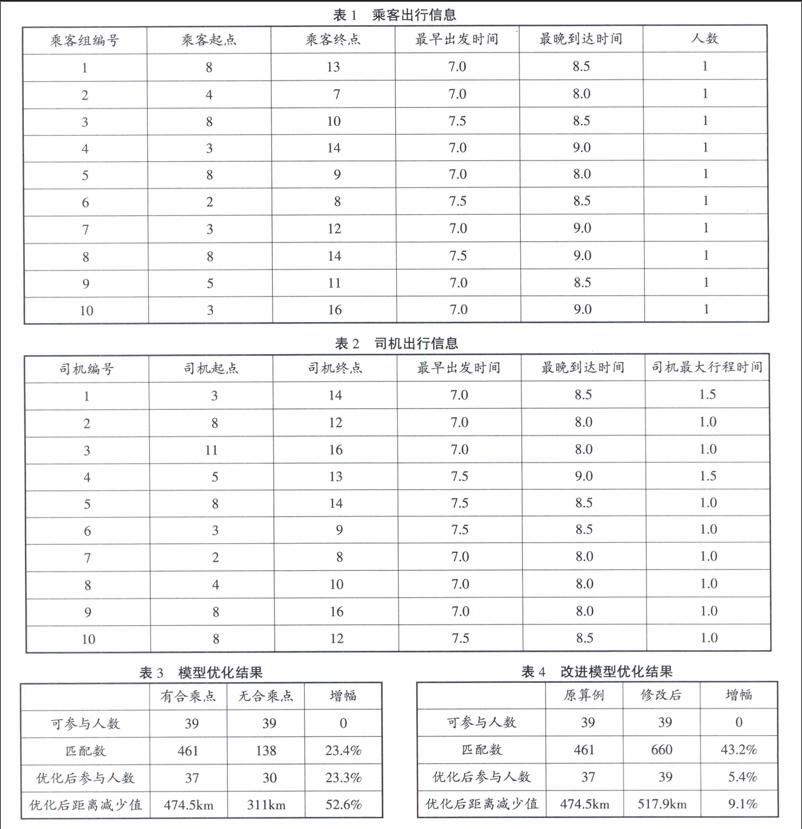
算例路网如图1所示。设定路网中共有22个节点。其中1~16节点为普通节点,17~22节点为合乘点。实线上数字表示两点间的距离(单位km)。设定路网节点之间可以相互直达,图中没有显示出所有节点间路线及其距离。路网中共有15位通勤司机,24位合乘乘客。设定机动车行驶速度40km/h,乘客步行速度为5km/h。机动车最大载客量统一设定为4人。司机乘客的部分出行信息分别见表1表2。endprint
司机能接受的最大行程时间算例中直接设置为司机通勤最晚到达时间与最早出发时间的差值。算例的匹配和优化部分利用软件Matlab编写程序进行运算。运算中在原有数据条件下分别设置了有合乘点和没有合乘点两種情况进行对比。结果如表3所示。
从表3中看出算例中无论有无合乘点,每一位司机以及乘客都可以参与到合乘中。加入合乘点后因为乘客的上车点和下车点增加,司乘匹配数显著增加,由138种增加到461种可能。优化后结果显示因为合乘点的加入,模型中参与人数由30位增加为37位,增加23.3%,其中有更多的乘客可以加入合乘模型中。路网中减少机动车行驶距离值由311km增加到474.5km,增加52.6%。
下面对路网中合乘点的选取范围进行修改,分析合乘点对合乘模型的影响。原例中节点2到节点17、节点8到节点19、节点10到节点20、节点15到节点22距离都超过1km,超出乘客的最大步行距离(1km),意味着从节点2、8、10、15出发的乘客不会选择步行到合乘点17、19、20、22。现将上4对节点间距离分别改为0.9、0.7、0.7、0.9,也就是为在节点2、8、10、15出发的乘客增加有效合乘点。对修改过的算例模型进行运算得出的结果如表4所示。
从表4中可以看出合乘点的选取范围扩大后,全部的司机和乘客都能参与到合乘中;路网中机动车行驶距离减少值更大,模型对缓解城市通勤高峰期的交通拥堵作用更明显。通过对比可以看出模型中参与者人数随着算例中有效合乘点数增加而增加,而路网机动车行驶距离随着有效合乘点数增加而减小。
3 结束语
针对城市交通中的通勤问题,本文提出了一种高峰时段通勤车辆的合乘模型,并给出了具体求解算法。通勤时段居民出行的集中性有助于实现网络合乘行为的整体优化。通过数值分析可知在城市通勤时段进行通勤车辆合乘可以有效地减少路网机动车需求数量,满足更多人的出行需求,从而缓解城市道路的交通压力。合乘点的加入使得模型中司乘匹配成功数量显著增加;通勤合乘参与人数和路网机动车行驶距离减少值也会随着更多合乘点的加入而不同幅度增加;有效合乘点的数量是取得合乘优化效果的关键。
参考文献:
[1] Cordeau J F, Laporte G. The dial-a-ride problem: models and algorithms[J]. Annals of Operations Research, 2007,153(1):29
-46.
[2] Parragh S N, Doerner K F, Hartl R F. Variable neighborhood search for the dial-a-ride problem[J]. Computers & Operations Research, 2010,37(6):1129-1138.
[3] 覃运梅,石琴. 出租车合乘模式的探讨[J]. 合肥工业大学学报(自然科学版),2006,29(1):77-79.
[4] 吴芳,李志成,徐琛. 出租车合乘制调度优化模型研究[J]. 兰州交通大学学报,2009,28(1):104-107.
[5] 祝进城,帅斌,孙朝苑,等. 固定费率下城市出租车拥挤收费模型与算法[J]. 计算机应用研究,2013,30(8):2288-2291.endprint
