分子动力学程序的面向对象C++设计与OpenMP并行化
2017-11-22冯剑
冯 剑
分子动力学程序的面向对象C++设计与OpenMP并行化
冯 剑
利用分子动力学模拟研究的对象越来越复杂,造成编程越来越困难,计算的工作量越来越大,利用面向对象和并行化技术可以有效解决这些问题。本文给出从分子动力学模拟研究的对象和过程抽象出面向对象模型的方法,着重讨论了OpenMP的并行化方法。对实际体系的模拟表明,该程序的并行效率很高,加速比接近于使用的CPU核心数。可以用来对更大的体系进行模拟研究。
分子动力学模拟;面向对象技术;并行化;C++语言;OpenMP
1 前言
随着计算技术的发展,计算科学与其他学科的交叉融合,利用计算机进行科学研究的计算与模拟方法已经发展成为与实验、理论并行的第三种科学研究手段。分子动力学(MD, Molecular Dynamics)模拟作为计算机模拟的一种重要方法在化学、化工等领域发挥越来越重要的作用。
MD模拟一般以牛顿力学为基础,建立体系中分子的运动方程,通过合适的积分格式对方程进行近似,利用计算机来数值求解每个分子的运动方程,得到每一时刻分子的坐标和动量,从而得到体系在相空间的运动轨迹。再利用统计方法来获得体系的静态和动态性质。目前已有很多商业化或开源的MD软件,如Discover、AMBER、Gromacs和LAMMPS等。
随着研究的深入,研究对象越来越复杂,模拟体系也变得越来越大,计算机处理的时间需要越来越长,需要充分利用计算资源对模拟程序进行并行化处理。并行化方法有很多种,对于具有多个运算节点的集群系统,常用的并行化方法是将任务分解到不同的运算节点,这些运行节点运行同一程序,这些程序彼此间通过消息传送接口机制来传送数据,即所谓的MPI ( Message Passing Interface)[1]。
当前的CPU一般都具有多个核心,其运算能力正变得愈加强大。充分利用这些核心进行并行化运算可以处理较大规模的计算任务。不同于MPI在进程级的并行,利用CPU核心的并行一般为线程级。单一的进程被划分为多个线程,计算任务被分解到这些线程上。这类编程方法大多需要考虑每个线程的执行细节,不太适合非计算机专业的科技工作者使用,且串行代码与并行代码间区别较大,使用串行程序验证并行方法的正确性需要更大的工作量。一种基于编译指令的OpenMP并行化方法获得科技工作者的广泛关注。
OpenMP方法只需要在需要并行的语句块前加上#pragma omp预编译指令,它不改变原串行代码。对于不支持OpenMP指令的编译器则依然通过编译,并按串行方式工作。OpenMP的并行机制是一个主线程,在并行指令下分岔(fork)出多个线程,这些线程共享内存,数据共享和同步非常方便。在并行语句块结束后产生的线程被销毁并再次并入(joint)主线程。OpenMP并行程序是一个不断发生Fork-Joint的过程,在Fork和Joint间为线程并行,其外为主线程串行[2]。
常见的计算集群系统,每个运算节点一般都具有二个及以上核心的CPU,因而使用MPI和OpenMP混合的并行化方法非常普遍[3]。无论是MPI还是OpenMP,一般都是利用CPU进行运算,其编程模型是同构的。当前利用GPU强大的浮点运算能力执行科学计算得到了越来越多的关注,CPU+GPU的异构编程技术发展很快。如NVIDIA的CUDA技术,苹果等公司研发的OpenCL技术等。为进一步降低编程难度,由NVIDIA等公司推动的OpenACC技术,它采用与OpenMP类似的编译指令方式来处理GPU编程是值得特别关注的。鉴于GPU高性能计算的迅猛发展,intel公司也推出了Xeon Phi芯片,最新的Xeon Phi 7290拥有72个核心288个线程,单/双精度浮点性能超过6/3TFlops。
利用现成的MD软件包可以很方便的开展研究工作,但囿于软件自身的限制,无法应用和发展新的方法、新的模型和新增的性质统计等。研究工作者自行编制程序并从事研究工作确有必要。作者多年前因研究工作需要,自行编制了MD软件程序MDSS(Molecular Dynamics Simulation Studio)。该程序早期使用C语言。随着研究对象复杂和多样化,程序规模越来越大,程序拓展和维护变得越来越困难。使用面向对象的C++语言可以较好的解决这些问题。另外考虑到实验室计算条件的实际情况,使用OpenMP技术实现并行化处理。
2 基于C++语言的面向对象设计
MD研究的典型步骤是将研究的分子放入一个模拟盒子中,给定每个原子的初始位置和速度。计算出每个原子受到的净作用力,选用一种积分格式如Velocity Verlet法,近似求解二阶微分方程组,得到下一时刻的位置和速度,再次计算该时刻的力和积分运算。不断循环该过程,获得系统的演化过程[4, 5]。
处于单一模拟盒子中的分子体系,必然有较多的表面分子,存在较大的表面效应,其性质与体相差别较大。为消除表面粒子,可对模拟盒子使用周期性边界条件。周期性边界条件必然造成以模拟盒子为单位的周期性结构,为降低其影响,模拟盒子中的分子数不能太少。
原子净的作用力由多种相互作用构成,1)不同原子间的非成键作用,它由非静电作用和静电库仑作用组成;2)两个相邻原子形成化学键间的键连作用;3)三个原子形成一定角度的键角作用;4)四个原子形成的两面角和非常规两面角作用等。另外,还包括特定系综和方法的额外作用力,如使用Langevin动力学方法时,每个原子受到的随机力和粘滞力[6]。
MD模拟中,计算量最大的是原子间的非成键作用。理论上,对于N个原子的体系,它需要处理N(N-1)/2个两两原子间的对相互作用力,即计算量与N2成正比或计算量为O(N2)阶。非静电作用一般使用Lennard-Jones(LJ)模型,它的势能在一定距离后迅速衰减到0,可以在一定距离处截断,因而看作短程作用,实际计算的作用力对远远小于N(N-1)/2个。可以使用Linked List或者邻位表方法将运算量降低到O(N)阶[4]。静电库仑作用属于长程作用,需要一些特定的算法,如PME法,它可以将运算降低到O(NlogN)阶[7]。分子中的这些相互作用的函数形式和参数有不同的选择,这些集合形成了所谓的力场。
根据分子动力学模拟过程,抽象出面向对象的模型则因人而异,没有统一标准。作者在解决该问题时本着“效率优先,兼顾性能”,即重点解决程序的可扩展性和代码重用性,在实现细节上考虑计算性能。
模拟程序的执行由TSimulation类负责。该类包含TSystem类(模拟盒子构建、分子插入等)、TIntegrator类(积分运算)、TEvaluateForce(计算力)、TLinkList类(使用Linked list方法计算非成键力)、TForceField类(选取某力场作为输入参数)、TMeasureProperty类(物理量统计)的对象。
TSystem类来自模拟体系抽象,TSimBox类和TMolecularSet类分别反映模拟盒子和分子集合。考虑到模拟系统由模拟盒子和多种类型的分子集合组成,TSystem类由TSimBox类和TMolecularSet类继承而来。模拟盒子和分子集合两者间差别巨大,没有相同的数据成员和方法,从TSimBox类和TMolecularSet类的多重继承会使得逻辑更为清晰。
TMolecularSet类处理体系所有分子,其中含有TMolecularGroup类的指针成员,每个TMolecularGroup对象表示某种分子。任何类型分子可能有多个分子,因此TMolecularGroup类包含TMolecule类的对象数组,数组的长度为分子数目。分子由多个原子组成,因而TMolecule类中包含TAtom类的对象数组。TAtom类包含了速度、力、位置和粒子类型等变量。
不同模拟条件或研究对象,计算力的类型可能并不相同,它可以通过模拟输入文件来指定,如在输入文件中使用[nobond]、[bond]语句块,表示体系需要计算非成键作用和键连作用。针对力计算,有一个抽象的虚基类TForce,它为各派生类提供一致的接口。非成键作用类TNonBondForces和键连作用类TChainForces均从这个虚基类继承而来。TEvaluateForce类有一个TForce类的二维指针数组**force,它通过Bind(TForce *pforce)方法向系统中追加需要计算的各种力。
系统的性质统计与力计算类似,可以选择性的统计不同性质。TMeasure是一个虚基类,具体的统计性质从该类继承,如TMeasureTherm统计常用的热力学性质,TMeasureDiffusion统计扩散系数等。TMeasureProperty则是一个容器类,有数据成员TMeasure **sum。
对于数值积分格式,本程序只选择Velocity Verlet法,NVT或NPT等系综的有不同的实现方法,如Berendsen方法[8],Nose-Hoover方法等[9]。本程序使用TIntegrator虚基类,不同的积分方法从该虚基类继承,如TBerendsenIntegrator和TNHIntegrator分别处理Berendsen法和Nose-Hoover方法。图1给出了主要类间的UML图,其中TMeasure和TMeasureTherm等类与TForce和TNonBondForces等类关系类似,为清晰简明该图没有绘制。另外,程序中使用的力场为Martini粗粒化力场[10]。
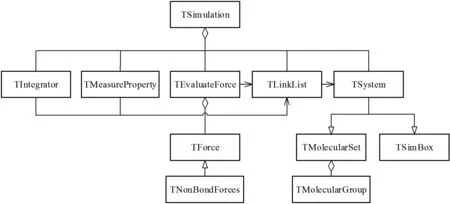
图1 模拟程序主要类的UML图
3 OpenMP的并行化
3.1 非成键作用
原子间的非成键作用是MD模拟中最耗时的运算。程序使用Linked List法,它是将空间划分为略大于截断距离的网格,记录每个网格中的原子。计算某原子的相互作用时,首先获取该原子所在的网格,计算它与该网格中的所有原子间的相互作用力,再计算它与自身元胞中26个相邻元胞(不重复计算,实际仅考虑其中的13个元胞)中所有原子间的作用力。Linked List需要每步更新列表。计算非成键力的核心代码如下:
double energy = 0, virals = 0;
for (int nz1 = 0; nz1 for (int ny1 = 0; ny1 for (int nx1 = 0; nx1 < NX; ++nx1) { //通过linked list查找所有相邻原子(由指向原子指针first和next索引) //计算原子间距离并计算力、势能和维里(代码略),累计力、势能和维里 first->Force() += fk; next->Force() -= fk; energy += rv; virials += rf; } } } 其中NX、NY和NZ表示三个维度划分的网格数目。程序对所有的元胞进行查找。其中的first和next是指向原子的指针。OpenMP并行化的关键是该for循环语句块的处理。OpenMP主要对循环次数固定的for并行,其格式如#pragma omp parallel for,其中#pragma为编译指令。对于多重循环而言,在外层循环中进行并行化远比内层循环并行化效率高。按OpenMP技术,此段代码的并行化操作仅需在第一层循环外添加如下并行指令 #pragma omp parallel for reduction(+:energy, virials) for (int nz1 = 0; nz1 < NZ; ++nz1) 统计的能量(energy)、维里(virials)在循环外部定义,每个线程共享这些变量,不同线程同时更新这些变量会存在竞争条件(race conditions)。在OpenMP中,数据同步操作有临界区(critical)、归约(reduction)和原子(atomic)等。不同编译器或系统三者开销并不相同,一般而言原子操作最小,而临界区最大。原子操作只能应用于单条语句。此处,对于energy和virials变量较适宜的是使用归约操作。 尽管指向原子的first和next指针是在并行块内部定义,属于私有变量,但对该变量指向的全局力,其累加过程中存在数据冲突。力为矢量,有三个分量。为了更好的处理力、位移和速度等向量,程序中定义了TVector类型,并为该类定义了运算符重载,因而无法使用归约操作。最方便的做法是该操作放入临界区,由不同线程独占运行从而避免冲突。其方法是将这些变量操作放在操作语句块中,前置critical指令即可,如 #pragma omp critical { first->Force() += fk; next->Force() -= fk; } 上述方法在体系较小,可用线程较多时无法获得较好性能。如对于包含500个水分子的立方型模拟盒子,NX、NY和NZ为3,1000个水分子值为4,显然对于这两个系统最多只能用3或4个线程。OpenMP 3.0对于for指令增加了collapse(参数)指令,指示编译器系统,将“参数”层循环合并处理,如#pragma omp parallel for collapse(2)将之后的两重循环合并[2]。但在OpenMP 2.0中没有提供相应的功能,不过可以对代码进行少量修改将上面的循环进行合并处理。只是在粒子数较少时,计算量也较小,并行化运算没有太大意义。 Velocity Verlet积分方法更新位置和速度需要两步操作,第一步更新位置和半时间步长的速度,第二步更新一个完整时间步的速度,在两步之间还需要计算新位置的力。由于粒子位置和速度更新完全独立,只要直接在for循环前添加相关指令即可。两步的并行化方法基本一致,其中第一步的核心代码如下。 #pragma omp parallel for (int i = 0; i < MolecularSpecies; ++i) { #pragma omp for for (int j = 0; j < MolecularNumbers[i]; ++j) for (int k = 0; k < MolecularLength[i][j]; ++k) { //获取指向原子指针*Atom,更新位置和半时间步长的速度 Atom->Velocity() += Atom->Force() * Mass[atom->Species()]; Atom->Position() += Atom->Velocity() * dt; } } 像上节那样简单的在第一重循环外放置#pragma omp parallel for,将按分子种类划分线程,并行效率可能非常低,如果仅有一种类型分子,则无法并行运行。如将该语句放置在最内层循环则fork-joint开销太大。考虑到一般情况下相同分子的分子数不会太少,将并行指令放在第一重循环外,#pragma omp for放在第二个循环中,这种parallel和for指令分离方式可以有效提高并行性能[10]。 本程序性质统计的抽象模型类似于力计算。程序定义了TMeasureProperty容器类,其中定义了统计各个性质的虚基类TMeasure的二重指针,即 TMeasure **sum; 如对于统计压力、势能等热力学性质的对象可以定义对象,并绑定到TMeasureProperty容器,相关代码如下 TMeasure *measuretherm = new TMeasureTherm(sys, force); sum->Bind(measuretherm); 性质统计的并行化在更大粒度上进行,每个统计性质使用一个线程,统计性质内部不再并行化,这些统计操作不再有数据冲突,仅需要在TMeasureProperty中的Evaluate函数中添加一条指令即可 void TMeasureProperty :: Measure(int step){ #pragma omp parallel for for(int i = 0; i < num; ++i) { sum[i]->Measure(step); } } 为考察程序的并行化效果,本文计算的硬件环境是Dell Precision 3620。CPU为E3-1225 v5 (四核),内存为8GB 2400MHz DDR4 UDIMM。操作系统为Windows 10 家庭版 64位。编译环境为Visual Studio Community 2015,内置OpenMP 2.0。 本文分别使用500、1000、5000、10000个水分子在温度为300K,密度为995.6g/cm3条件下执行NVT系综模拟,恒温方法选择Berendsen法。时间步长为10-2fs,执行10000步模拟。每个体系运行四个单独模拟,平均求出运算时间。体系的各种统计性质,并行程序给出了与串行程序完全一致的结果,并行方法没有问题。图2不同粒子数不同线程的计算时间和平行效率。本文的并行效率是相同条件下串行运算时间除以并行运算时间。首先从该图可以看出,并行效率很高,对于10000个粒子串行花费的时间约为四个线程的3.2倍,两个线程的1.8倍,接近于线程数4和2;其次,无论是串行还是并行,计算时间与粒子数基本上成正比。另外,体系水分子数很少时(如本文500个),由于网格数较小,未能很好地利用线程,并行效率不高。 图2 不同粒子数体系的串行与并行运算时间和并行效率 科学计算的主流语言如Fortran、C++等都具有面向对象拓展,使用面向对象技术对分子模拟程序进行设计可以大大降低复杂体系的编程难度,提高编程效率,同时不会明显降低程序的运算速度。当前计算机的硬件技术已发生较大变化,多核CPU已成为主流,配备二个多核CPU的工作站已非常普遍。本文研究表明,基于面向对象方法并采取OpenMP技术并行化模拟程序可以达到很高的并行效率,个人计算机或工作站完全可以模拟较大规模的体系,揭示更复杂的物理或化学现象。 [1] 都志辉编著. 高性能计算并行编程技术—MPI并行程序设计[M].北京:清华大学出版社, 2001:15-18. [2] Barbara Chapman, Gabriele Jost, Ruud van der Pas. Using OpenMP - Portable Shared Memory Parallel Programming[M].Massachusetts:The MIT Press, 2008:23-24, 35-50, 312. [3] Michael J Quinn著, 陈文光, 武永卫等译. MPI与OpenMP并行程序设计[M].北京:清华大学出版社, 2004:350-360. [4] Allen M P, Tildesley D J. Computer Simulation of Liquids[M].Oxford: Clarendon Press, 1987:71-105, 149-152. [5] Frenkel, Smit著, 王文川等译. 分子模拟—从算法到应用[M],.北京:化学工业出版社, 2002:51-92. [6] Feng J, Liu H, Hu Y. Molecular dynamics simulations of polyampholyte solutions: osmotic coefficient[J].Molecular Simulation, 2006, 32(1), 51-57. [7] Darden T, York D, Pedersen L. Particle mesh Ewald: An Nlog(N) method for Ewald sums in large systems[J].J. Chem. Phys., 1993, 98(12):10089-10092. [8] Berendsen H J C, Postma J P M, van Gunsteren W F, DiNola A, Haak J R. Molecular dynamics with coupling to an external bath[J].J. Chem. Phys., 1984, 81(8):3684-3690. [9] Hoover W G. Canonical dynamics: Equilibrium phase-space distributions[J].Physical Review A, 1985, 31(3): 1695-1697. [10] Marrink S J, Risselada H J, Yefimov S, Tieleman D P, de Vries A H. The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations[J].J. Phys. Chem. B, 2007, 111(27):7812-7824. ObjectOrientedC++DesignandOpenMPParallelizationoftheMolecularDynamicsProgram Feng Jian The object studied by using molecular dynamics simulation becomes more and more complex, which results in the programming more difficult and the computation workload bigger. The use of object-oriented and parallel technology can effectively solve these problems. Through the objects and the process of the molecular dynamics simulation, this paper gives the modelling of the object-oriented method, emphatically discusses the parallelization method of OpenMP. The simulations of actual system show that the program has the high parallel efficiency, and the speedup is close to the CPU core number, which can be used to simulate the larger systems. molecular dynamics simulation;object oriented technology; parallelization; C++ language; OpenMP O642.5 A 1673-1794(2017)05-0020-05 冯剑,滁州学院材料与化学工程学院教授,博士,研究方向:分子模拟(安徽 滁州 239000)。 国家自然科学基金:表面活性剂的界面传递行为研究(21476072) 2017-06-15 责任编辑:李应青3.2 数值积分
3.3 性质统计
4 结果与讨论
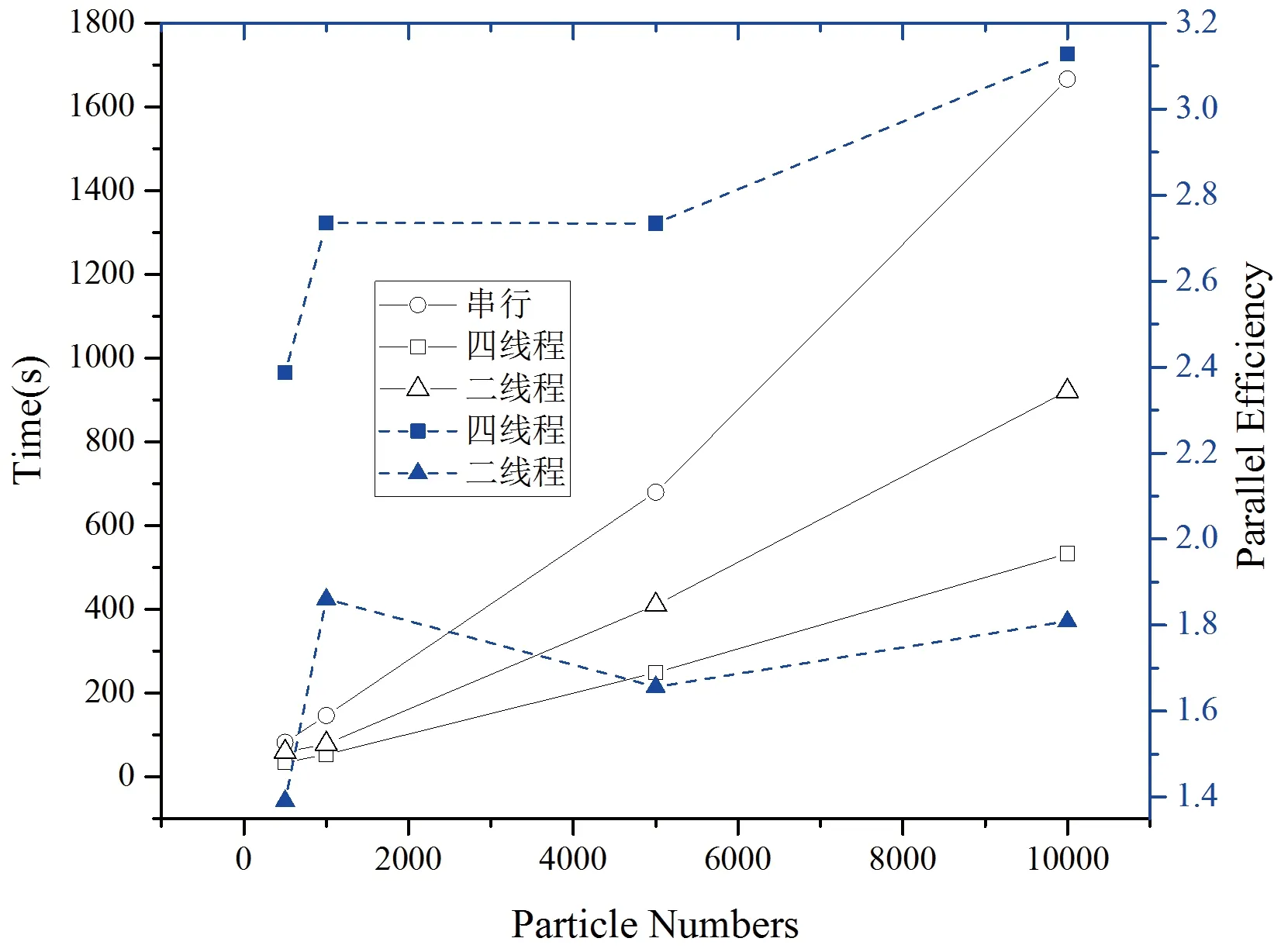
5 结论
