基于CFD的小尺度桩柱流固耦合分析及波浪力求解
2017-11-22张力伟,李昕,赵颖华
张 力 伟, 李 昕, 赵 颖 华
( 1.大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024; 2.新誉集团有限公司, 江苏 常州 213166; 3.大连海事大学 道路与桥梁工程研究所, 辽宁 大连 116026 )
基于CFD的小尺度桩柱流固耦合分析及波浪力求解
张 力 伟*1,2, 李 昕1, 赵 颖 华3
( 1.大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024; 2.新誉集团有限公司, 江苏 常州 213166; 3.大连海事大学 道路与桥梁工程研究所, 辽宁 大连 116026 )
基于Workbench平台建立了软土地基圆柱桩波浪作用分析的三维数值波浪水池,实现了线性波的数值模拟及波浪与桩柱的双向流固耦合分析,并得到波浪力数值解.对于小尺度桩柱,桩柱为刚性时其所受波浪力与《港口与航道水文规范》中规范解一致.考虑桩柱的柔性及流固耦合时,在达到峰值的位置波浪力与规范解相比既有增大也有减小,桩柱总波浪力最大增大5.7%,桩底弯矩最大增大54%.而采用直接加载法即不考虑流固耦合时桩柱的振动幅值大于耦合时桩柱振动,桩底弯矩最大,大于规范解84.6%.因此,在进行小尺度柔性桩柱设计时应采用流固耦合方法.
CFD;数值波浪水池;流固耦合;波浪力;小尺度桩柱
0 引 言
圆柱桩是海洋工程比较常见的结构形式,其在波浪荷载作用下的动力响应问题一直是工程设计中备受关注的重点.1950年Morison等提出了计算小尺度结构波浪力的经验公式[1],至今仍广泛使用.但是当结构本身的振动较大会对波浪力造成改变时,需考虑结构与波浪之间的流固耦合效应.Sarpkaya等[2]及Fish等[3]分别提出了考虑相对运动的修正Morison方程及基于附加质量的简化公式.基于这一思想,国内的一些学者针对海洋桩基的流固耦合问题进行了一系列的研究[4-7],取得了很好的成果.但是此过程需要不断迭代计算,工程计算量大,对于一般的工程技术人员来说过于繁复.而对于大直径结构物所受波浪力,通常采用绕射理论来求解[8],我国《港口与航道水文规范》[9]给出了桩柱最大水平总波浪力的简化计算公式,但是不能考虑流固耦合效应.在这种情况下,寻求一种通用的能够适用于不同结构尺寸的数值解析方法就显得尤为必要,在工程上具备重要价值.
近年来,计算流体动力学(CFD)分析方法已经被证明能够成功地模拟波浪运动,在构建数值波浪水池方面已经得到了广泛的应用[10-11].本文基于CFD方法,采用双向流固耦合技术实现小尺度桩柱波浪作用的模拟分析,并对波浪力进行求解,以期为海洋工程桩基动力学精确求解提供一个有效的手段.
1 理论基础
1.1 双向流固耦合原理
假设流体为不可压缩的理想流体,则离散后的流体运动方程[12]为
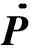
Mf
+KfP=Ff-Rf
(1)
式中:Mf为流体质量矩阵;Kf为流体刚度矩阵;P为流体整体压力向量;Ff为流体外荷载;Rf为耦合面荷载阵列,表达式为

Rf=ρS
(2)
(3)
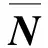
作用在结构表面上的流体压力荷载为
Rs=STP
(4)
考虑流体压力后,有阻尼结构动力控制方程为

Ms

+Cs
+KsU=Fs+Rs
(5)
式中:Ms为结构整体质量矩阵,Ks为结构整体刚度矩阵,Cs为结构阻尼矩阵,Fs为结构外荷载.
综合式(1)和(5),即可对流固耦合作用下结构响应进行求解.
1.2 小尺度桩柱波浪力
桩柱波浪力的计算参考我国《港口与航道水文规范》.对于D/L≤0.2的小尺度桩柱,H/d≤0.2且d/L≥0.2时,作用于水底面以上高度z处单位长度桩柱上的水平波浪力可按Morison公式计算:

(6)

(7)

(8)

(9)
式中:PD为波浪力的速度分力;PI为波浪力的惯性分力;CD为速度力因数,对圆形断面取1.2;CM为惯性力因数,对圆形断面取2.0;D为桩柱直径;A为桩柱的横断面积;u为桩柱所在位置流体质点速度;L为波长;H为波高;T为波浪周期;k为波数;d为水深;γ为水的重度;g为重力加速度;ω为波浪的角频率;t为时间,当波峰通过桩柱中心线时t=0.
若结构振动较大,考虑流固耦合对波浪力的影响,高度z处桩柱波浪力可表示为
PW=PD+PI=

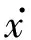
x.
)|(u-
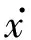
x.
)|+

γgA∂u∂t+γgCmA(∂u∂t-x..)
(10)
其中
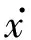
x.
、

x..
分别为桩柱相应高度对应的速度和加速度,Cm为附加质量因数.可见,当结构运动速度、加速度与流体质点运动方向相同时波浪力减小,反之增大.
作用于小尺度桩柱整个桩柱高度上的任意相位时的正向水平总波浪力P,可按下式计算:
P=PDmaxcosωt|cosωt|-PImaxsinωt
(11)
其中PDmax为作用于整个桩柱高度上的最大速度力,PImax为作用于整个桩柱高度上的最大惯性力,可按下列方法确定:
方法1沿桩柱高度选取不同的z值,按式(6)分别计算不同高度的PDmax和PImax,计算点不少于5个,其中包括z=0、d和d+η3点.计算PDmax时,η=ηmax;计算PImax时,η=ηmax-H/2;ηmax按规范给出的图表进行确定.求出不同高度处的PDmax和PImax后即可得到总的PDmax和PImax.
方法2高度z1和z2之间区段上PDmax和PImax按下列公式计算:
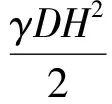
(12)

(13)
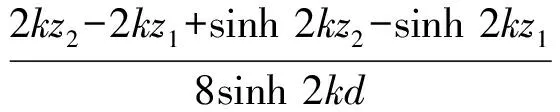
(14)
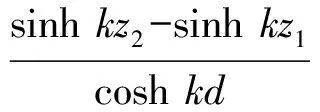
(15)
计算PDmax时,取z1=0,z2=d+ηmax;计算PImax时,取z1=0,z2=d+ηmax-H/2.
方法2同样适用于桩柱局部高度上的波浪力计算.
2 数值模型
采用ANSYS Workbench平台建立流固耦合数值仿真模型,其中流体和结构部分的仿真分别由平台内置的Fluent模块和Transient Structural 模块完成,耦合计算由System coupling 模块完成.
数值波浪水池长60 m,宽10 m,高12 m,水深d=10 m,水面以上2 m为空气,由于规范在计算波浪力时采用的是线性波,为便于对比,本文采用线性波进行模拟.设定波高H=1.8 m,波长L=23 m,周期T=4 s.桩柱高出水池上表面5 m,桩柱中心线与左侧波浪入口距离6 m.小尺度桩直径1.5 m,壁厚0.014 m,桩顶附加一个60 t的集中质量块.为模拟软土中桩的运动,依据《港口工程桩基规范》中对等效桩长的建议,水底以下建立一段6倍桩径长度的等效桩,桩底全约束.
网格划分全部采用结构化网格,水池长度方向网格尺寸0.3 m,高度方向自由水面上下2 m范围内网格尺寸0.2 m,自由水面以下2 m至水池底面网格尺寸0.4 m,结构网格与流体网格在耦合面上重合.数值模型见图1.

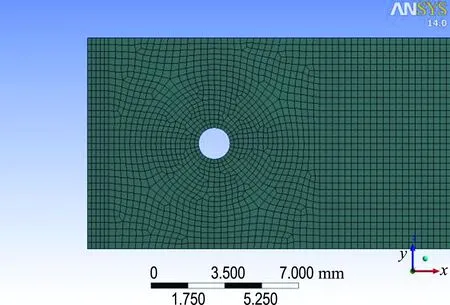
图1 波浪水池模型
数值造波采用速度入口造波方法,使用两相流模型VOF捕捉自由波面.水池左侧边界为速度入口边界,根据线性波波面方程[13]确定不同时刻入口的波面高度,波面以下水的体积分数为1,密度998.2 kg/m3,并按线性波理论确定其水平和垂直方向的速度分量;波面以上为空气,水的体积分数为0,空气密度1.225 kg/m3,入口速度为0;入口处两相介质的体积分数和速度分量通过UDF接口导入.水池上、下表面及桩柱耦合面设置为固壁边界,前后两个边界为对称边界,右侧出口边界设置为自由出流.模型计算考虑重力影响,设置运行环境参考工作压力为101 325 Pa,工作流体密度为1.225 kg/m3.
动网格设置:动网格采用动态光顺法,耦合面动网格类型为System coupling,上、下壁面动网格类型为Deforming.流固耦合面的数据传递方式为力耦合及位移协调,流固耦合面将压力荷载传递给结构耦合面,结构耦合面反过来将位移传递给流固耦合面.计算过程中对耦合面阻力进行实时监测得到桩柱上的波浪力.波浪力沿桩柱高度分两段进行监测,其中局部段高度为8.0~8.4 m,用于评估局部波浪力,另一段监测耦合面剩余部分,两者相加即为整个桩柱上的波浪力.为便于对比,同时计算了桩柱为刚性时的情况,此时只计算流体域即可,并关闭动网格选项.
湍流模式选用RNGk-ε模型,湍流强度根据雷诺数确定;动量方程、湍动能、湍动耗散率方程采用二阶迎风格式;压力速度耦合方式采用PISO.设置总计算时长为15 s,时间步长0.01 s,每步最大迭代次数10次.
3 计算结果与分析
图2为考虑结构耦合振动情况下t=12 s时波浪水池中波面形状与桩柱变形情况,可以看出,桩柱由于具有一定的柔度,在波浪力作用下随波面发生摆动.图3给出了距入口3 m处CFD模拟得到的波面变化曲线与理论解的对比.可以看出,在第1个周期内,CFD模拟没有得到完整的波高,波高与理论解相差较大;而第2个周期以后波高与理论解基本一致,说明数值模型准确可靠.

图2 波面形状与桩柱变形
图4给出了相同时刻过桩柱中心线纵剖面的局部波面形状及流体速度矢量,图中显示,在桩柱迎波面有一定的波面壅高产生,桩柱前后存在微小的水位落差.桩柱附近流体速度垂直向上,说明此时桩柱所受水平速度分力最小,而惯性分力最大.图5为同一时刻桩柱周围流体的速度流线,可以看出,桩柱周围流线较为平滑,没有漩涡产生,桩柱对波浪的扰动较小.

图3 距入口3 m处波面高度变化曲线
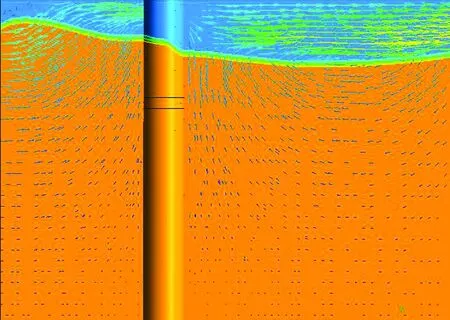
图4 波面及速度矢量

图5 桩柱周围速度流线
图6为计算时域内桩顶位移、速度和加速度曲线.桩柱的振动由低频振动和高频振动两部分组成,其中低频振动振幅较大,周期与波浪周期基本一致,说明桩柱的运动状态受波浪运动控制.加速度峰值为0.19 m/s2,相对于波浪质点的加速度峰值来说数值较大,会对波浪力产生影响.
图7给出了不考虑结构振动时桩柱局部波浪力的数值解与Morison法和规范方法2的计算结果的对比.不考虑结构振动引起的耦合时,波浪力

(a) 位移

(b) 速度

(c) 加速度
图6 考虑耦合时桩顶位移、速度和加速度曲线
Fig.6 Top pile displacement, velocity and acceleration curves considering coupling interaction

图7 不考虑耦合桩柱局部波浪力
数值解与规范解具有很好的一致性,数值方法求得的波浪力峰值与规范方法2的计算结果比较接近,而Morison法求得的波浪力峰值相对较小.
图8为采用CFD法得到的考虑结构振动和不考虑结构振动时桩柱局部波浪力对比,可以看出,在波浪力达到峰值的整周期位置,耦合工况的波浪力峰值既有增大也有减小.由计算可知,本算例中PDmax≤0.5PImax,桩柱所受最大波浪力近似等于最大惯性力,因此耦合作用下波浪力峰值的影响主要取决于桩柱对流体质点的相对加速度.结合图5中加速度曲线可知,在t=4,10,14 s时结构振动加速度较大,方向与桩柱所在位置流体质点加速度方向相反,因此波浪力峰值增大,最大增幅9%.而t=12 s时结构加速度与桩柱所在位置流体质点加速度方向一致,波浪力峰值减小.
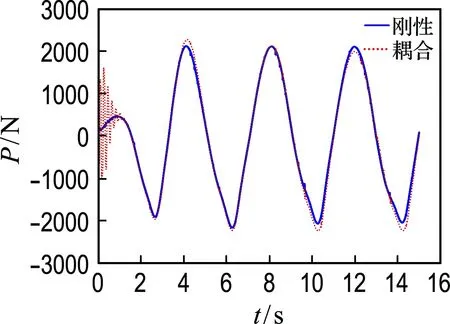
图8 考虑耦合桩柱局部波浪力
图9为考虑桩柱柔性耦合和桩柱为刚性时整个桩柱上总波浪力与规范方法2规范解的对比,可以看出,桩柱为刚性时桩柱总波浪力与规范解接近,而考虑柔性耦合时,桩柱总波浪力峰值影响规律与局部波浪力影响规律基本一致,在t=12 s时波浪力峰值减小,t=4,10,14 s时波浪力峰值增大,最大增幅5.7%.
为评估流固耦合作用对结构振动的影响,将桩柱波浪力规范解直接加载到对应的桩柱位置求出不考虑流固耦合时桩柱的振动响应(直接加载法).图10为不考虑流固耦合时桩顶位移、速度和加速度曲线,可以看出,不考虑流固耦合作用时桩顶的振动幅值大于考虑流固耦合时桩顶的振动幅值,说明流固耦合对结构的振动有阻尼作用.

图9 桩柱总波浪力

(a) 位移
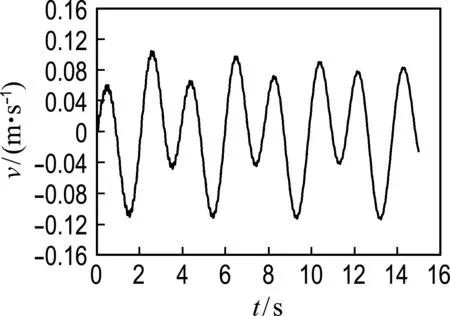
(b) 速度
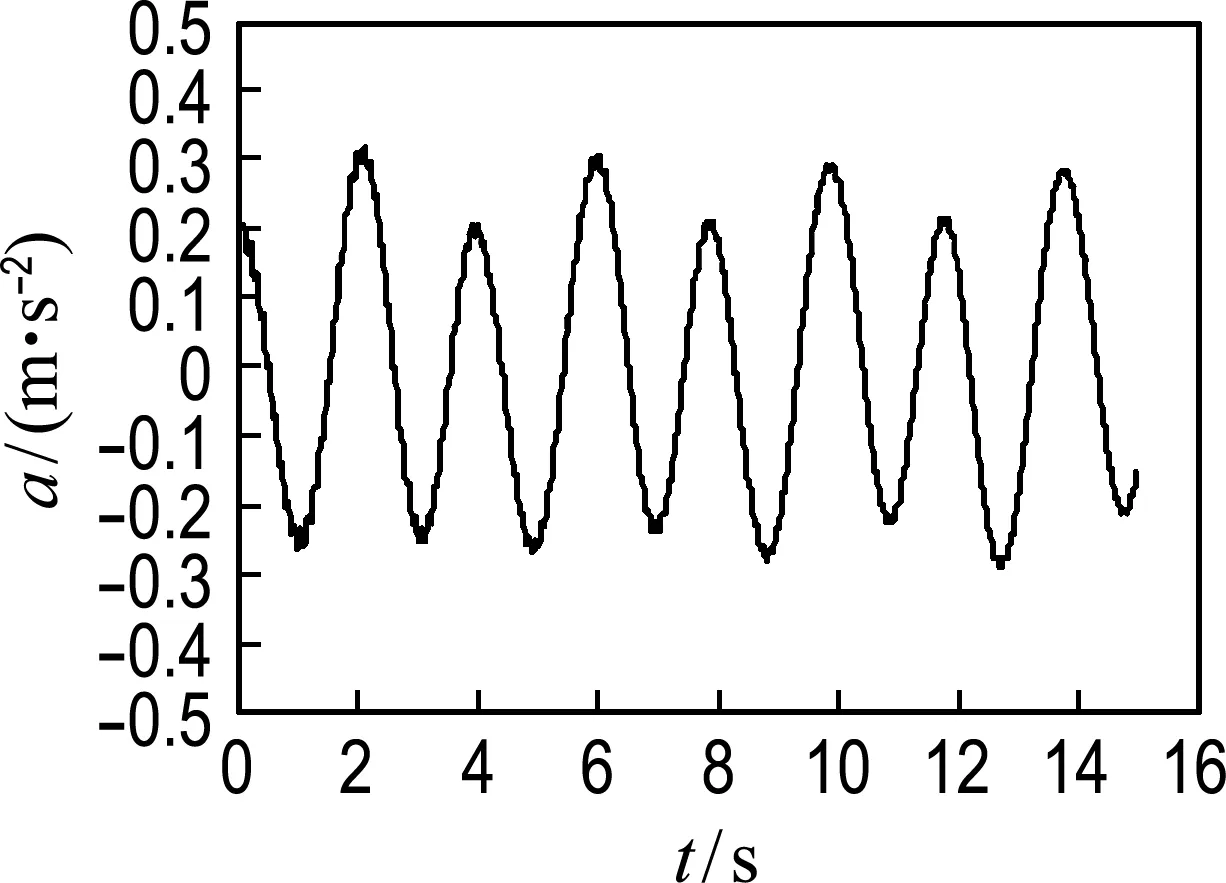
(c) 加速度
图10 不考虑耦合时桩顶位移、速度和加速度曲线
Fig.10 Top pile displacement, velocity and acceleration curves without considering coupling interaction
图11为两种工况下求得桩底弯矩与规范解(桩柱为刚性)对比,可以看出,规范方法2求得桩底弯矩最小,耦合情况下桩底弯矩大于规范解,最大增大54%.而采用直接加载法即不考虑流固耦合时桩底弯矩最大,大于规范解84.6%.因此,在进行小尺度柔性桩柱设计时若采用直接加载法则结果偏保守,应采用流固耦合方法.

图11 桩底弯矩
4 结 论
(1)对于小尺度桩柱,桩柱对波浪运动的扰动较小,桩柱周围速度流线较为平滑.桩柱的振动由低频振动和高频振动两部分组成,桩柱的运动状态基本受波浪运动控制.
(2)不考虑流固耦合时,小尺度桩柱波浪力数值解与规范方法2的计算结果比较接近,而Morison 法求得的波浪力峰值相对较小.考虑流固耦合时,在波浪力达到峰值的整周期位置波浪力既有增大也有减小,桩柱总波浪力最大增大5.7%.
(3)不考虑流固耦合作用时桩顶的振动幅值(直接加载法)大于考虑流固耦合时桩顶的振动幅值,说明流固耦合对结构的振动有阻尼作用.流固耦合情况下桩底弯矩大于规范解,最大增大54%.而采用直接加载法即不考虑流固耦合时桩底弯矩最大,大于规范解84.6%.因此,在进行小尺度柔性桩柱设计时应采用流固耦合方法.
[1] MORISON J R, JOHNSON J W, SCHAAF S A. The force exerted by surface waves on piles [J].JournalofPetroleumTechnology, 1950,2(5):149-154.
[2] SARPKAYA T, ISAACSON M.MechanicsofWaveForcesonOffshoreStructures[M]. New York: Van Nostrand Reinhold Company, 1981:25-32.
[3] FISH P R, DEAN R B, HEAF N J. Fluid-structure interaction in Morison′s equation for the design of offshore structures [J].EngineeringStructures, 1980,2(1):15-26.
[4] 张学志,黄维平,李华军. 考虑流固耦合时的海洋平台结构非线性动力分析[J]. 中国海洋大学学报, 2005,35(5):823-826.
ZHANG Xuezhi, HUANG Weiping, LI Huajun. Nonlinear dynamic analysis of offshore platform considering fluid-structure interaction [J].PeriodicalofOceanUniversityofChina, 2005,35(5):823-826. (in Chinese)
[5] 徐亚洲,李 杰. 结构流固耦合波浪动力响应的一阶预估校正法[J]. 船舶力学, 2012,16(7):781-786.
XU Yazhou, LI Jie. First order prediction correction method for dynamic wave responses considering fluid-structure-interaction [J].JournalofShipMechanics, 2012,16(7):781-786. (in Chinese)
[6] 王元战,龙俞辰,王朝阳. 考虑流固耦合影响的桩基波浪力简化计算方法[J]. 水道港口, 2014,35(2):93-98.
WANG Yuanzhan, LONG Yuchen, WANG Chaoyang. Simplified calculation method for wave force of piles under effect of fluid-structure interaction [J].JournalofWaterwayandHarbor, 2014,35(2):93-98. (in Chinese)
[7] 邓 露,肖志颖,黄民希,等. 考虑流固耦合的近海风机动力响应数值计算[J]. 湖南大学学报(自然科学版), 2015,42(7):1-8.
DENG Lu, XIAO Zhiying, HUANG Minxi,etal. Numerical simulation of dynamic response for offshore wind turbines including fluid-structure interaction [J].JournalofHunanUniversity(NaturalSciences), 2015,42(7):1-8. (in Chinese)
[8] 俞聿修,柳淑学. 随机波浪及其工程应用[M]. 大连:大连理工大学出版社, 2000.
YU Yuxiu, LIU Shuxue.RandomWaveandItsApplicationstoEngineering[M]. Dalian: Dalian University of Technology Press, 2000. (in Chinese)
[9] 中华人民共和国交通部. 港口与航道水文规范: JTS 145—2015 [S]. 北京:人民交通出版社, 2015.
Ministry of Transport of China. Code of Hydrology for Harbor and Waterway: JTS 145-2015 [S]. Beijing:China Communications Press, 2015. (in Chinese)
[10] 李金宣,柳淑学,HONG Keyyong. 非线性波浪的数值模拟[J]. 大连理工大学学报, 2008,48(3):430-435.
LI Jinxuan, LIU Shuxue, HONG Keyyong. Numerical simulation of nonlinear waves [J].JournalofDalianUniversityofTechnology, 2008,48(3):430-435. (in Chinese)
[11] 李宏伟. 数值水池造波方法研究[D]. 哈尔滨:哈尔滨工程大学, 2009.
LI Hongwei. Study on method of numerical wave generating [D]. Harbin: Harbin Engineering University, 2009. (in Chinese)
[12] 薛 杰,何尚龙,杜大华,等. 充液容器流固耦合模态仿真分析研究[J]. 火箭推进, 2015,41(1):90-97.
XUE Jie, HE Shanglong, DU Dahua,etal. Study on fluid-structure coupling modal simulation of liquid filling container [J].JournalofRocketPropulsion, 2015,41(1):90-97. (in Chinese)
[13] 竺艳蓉. 海洋工程波浪力学[M]. 天津:天津大学出版社, 1991.
ZHU Yanrong.WaveMechanicsforOceanEngineering[M]. Tianjin:Tianjin University Press, 1991. (in Chinese)
FSIanalysisofsmallscalepileandsolutionofwaveforceusingCFDmethod
ZHANGLiwei*1,2,LIXin1,ZHAOYinghua3
(1.StateKeyLaboratoryofCoastalandOffshoreEngineering,DalianUniversityofTechnology,Dalian116024,China;2.NewUnitedGroup,Changzhou213166,China;3.InstituteofRoadandBridgeEngineering,DalianMaritimeUniversity,Dalian116026,China)
Three dimension numerical wave tank is established on Workbench platform for analysis of cylinder pile in soft soil foundation under wave actions. Simulation of linear wave and two-way fluid-structure interaction(FSI) analysis are realized, and numerical results of wave force on cylinder are obtained. For small scale pile, the wave forces obtained using CFD method are consistent with the results using standard method given in Code of Hydrology for Harbor and Waterway when the pile is treated as rigid, but when the pile is treated as flexible and considering the coupling action between the pile and water, the peaks of wave force increase or decrease indefinitely, the maximum total wave force increases by 5.7% and the bending moment at pile bottom increases by 54%. The pile vibrations when neglecting the fluid coupling are greater than that considering the coupling, and the bending moment at pile bottom using direct loading method which doesn′t consider the fluid coupling increases by 84.6% than that using standard method. Therefore, FSI method should be applied in design of small scale flexible piles.
CFD; numerical wave tank; fluid-structure interaction (FSI); wave force; small scale pile
1000-8608(2017)06-0615-07
TK83;TU312
A
10.7511/dllgxb201706010
2017-03-10;
2017-09-17.
国家自然科学基金创新研究群体项目(51421064).
张力伟*(1982-),男,博士,高级工程师,E-mail:zlw_1982@163.com.
