悬臂梁结构串级无线预测控制算法研究及验证

杨 常 平， 喻 言*,2， 李 芦 钰， 冷 晓 智， 张 帅 帅， 欧 进 萍

( 1.大连理工大学 电子信息与电气工程学部， 辽宁 大连 116024； 2.辽宁省集成电路技术重点实验室, 辽宁 大连 116024； 3.大连理工大学 土木工程学院， 辽宁 大连 116024 )

悬臂梁结构串级无线预测控制算法研究及验证

杨 常 平1， 喻 言*1,2， 李 芦 钰3， 冷 晓 智1， 张 帅 帅1， 欧 进 萍3

( 1.大连理工大学 电子信息与电气工程学部， 辽宁 大连 116024； 2.辽宁省集成电路技术重点实验室, 辽宁 大连 116024； 3.大连理工大学 土木工程学院， 辽宁 大连 116024 )

应用无线方式对结构进行主动控制已经有了初步研究，并逐步取代传统的有线控制策略．无线方式不可避免地引入了延时，影响了系统稳定和控制效果，所以无线主动控制必须要解决延时问题．基于悬臂梁结构搭建了无线控制实验系统，采用PID和模型预测控制相结合的串级控制策略，增加了延时补偿算法，分别以无延时、信号采集端有延时、信号采集端及控制信号输出端都有延时3种工况，对悬臂梁无线控制系统进行了仿真与实验．仿真和实验结果表明，所建立的无线控制系统可以对模型结构实现控制，所运用的延时补偿策略能达到与有线控制相媲美的控制效果，对实际工程应用具有很好的借鉴作用．

延时补偿；无线控制；悬臂梁；预测控制

0 引 言

土木结构在受到地震、飓风等影响时会产生振动，当超过自身承受范围时结构就会失效甚至毁坏，所以需要对土木结构进行振动控制．传统的减振控制多为有线控制，布线复杂、维护困难，而无线方式布线少、系统的复杂程度低，且能根据实际需要更新传感器节点的布设，但是不可避免地引入了延时．喻言等[1]验证了无线传感器网络在海洋平台结构振动检测与控制上应用的可行性．赵永春等[2]设计并验证了基于压电元件同步开关阻尼技术的半主动振动控制．实际上，无线控制研究中从系统搭建、新型控制算法设计、延时处理等均面临全新的挑战．本文以悬臂梁模型为研究对象，构建无线控制实验系统：无线模块采用基于WiFi的嵌入式系统模块，控制器采用PID控制和模型预测控制相结合的串级控制方法，结合基于有限差分和变量代换的延迟补偿策略，经压电片驱动使悬臂梁形变，从而进行闭环控制．

1 悬臂梁结构无线控制系统设计

悬臂梁结构无线控制实验系统结构如图1所示，主要包括悬臂梁、位移传感器、无线发送与接收器、控制器、功率放大器以及压电驱动器．本实验的悬臂梁采用不锈钢梁．实验时，给钢梁一个初始状态，通过放置于梁上的激光位移传感器来测量悬臂梁末端位移，位移信号经调理电路和AD 转换后送入无线发送单元，无线接收单元接收到信号后送入dSPACE 控制器，控制器根据串级控制算法计算并输出最优控制力，最优控制信号经

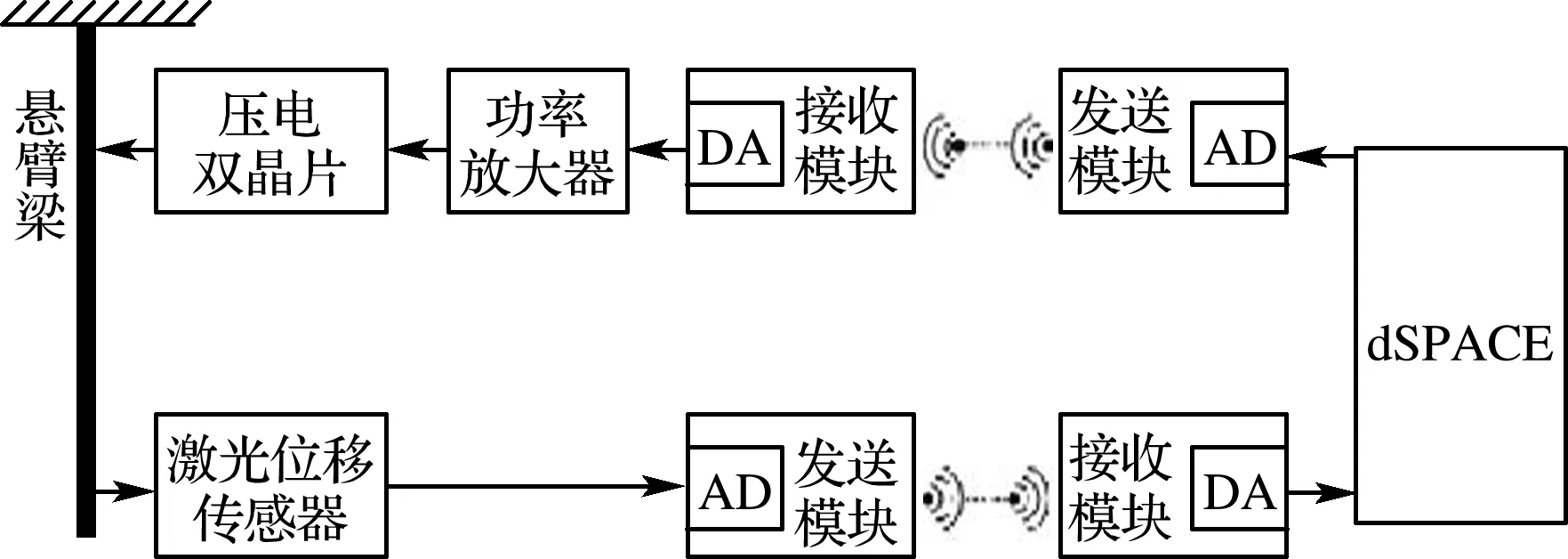
图1 系统结构

过无线发送单元传递出去，无线接收单元接收到控制信号后经过DA转换为模拟信号，再由放大器放大，以驱动压电驱动器产生足够大的形变，从而抑制梁的振动．实验现场如图2所示．

图2 实验现场

2 系统建模

如图3所示，悬臂梁的一端固定，在靠近梁固定端处粘贴有压电片，根据逆压电效应，压电片在电压的作用下可以产生形变，因此压电片在此处作为驱动器．悬臂梁模型及压电片参数如表1所示．

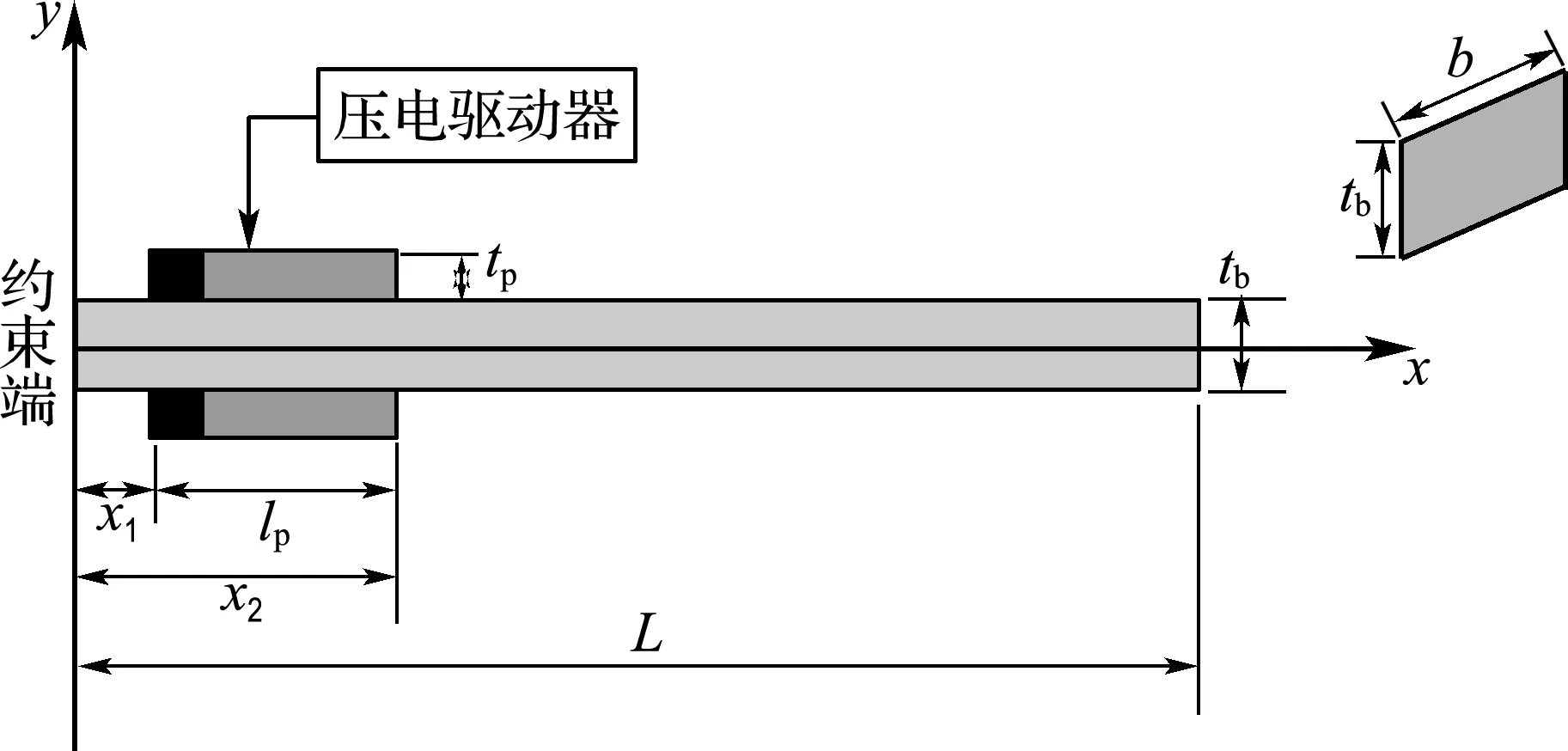
图3 悬臂梁结构

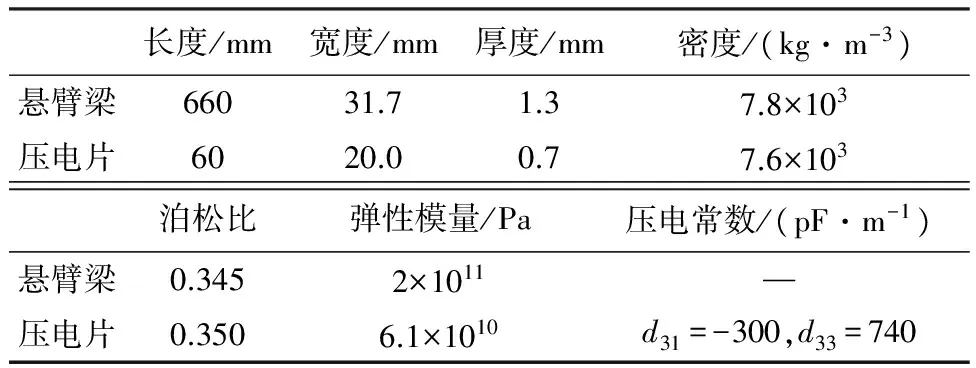
表1 悬臂梁及压电片参数

悬臂梁在外力作用下的动力学方程为

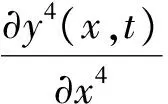
(1)

式中：EI为梁的弯曲刚度，ρ为梁密度，S为截面积．当在压电驱动器上施加电压u(t)，它绕压电梁的中性轴产生应力σ．该应力使梁产生力矩

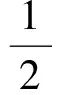
h(x-x1)]

(2)

化简方程，令

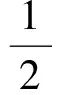
(3)

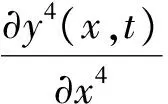
(4)

其中h(x)为阶跃函数．将式(4)乘以第i阶模态振型φi(x)并积分，有

(5)

i(t)+2ξiωi

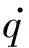
q．

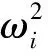
(6)

其中ξi为第i阶模态阻尼比．引入状态量：

x(t)=(q

q．

)T=

(q1(t)q2(t) …qn(t)

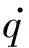
q．

1(t)

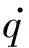
q．

2(t) …

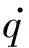
q．

n(t))T

(7)

则压电柔性悬臂梁的状态空间方程可表示为

(t)=Ax(t)+Bu(t)
y(t)=Cx(t)

(8)

(9)

3 带有延时补偿的控制算法设计

3.1 串级控制

多个控制器相互串联组成多级控制即为串级控制[3]．对于一套具有双控制器的串级控制系统，被控对象的状态信息经由主控制器计算得到中间量，该量作为输入经副控制器计算得到输出再作用于被控对象[4]．该串级控制系统实际上构成了两个闭环控制，一个是对控制量进行大概估算的内环控制，一个是对控制量进行精细计算的外环控制．外环控制回路称为主回路，内环控制回路称为随动回路，内外结合从而完成对控制量有着较高要求的控制过程[5-6]．这里，无论主回路或随动回路都有各自的被控对象、变送器和调节器．

本控制器算法部分采用串级控制模式．其中，PID算法作为内环控制器，输出为控制力；模型预测控制算法作为外环控制器，输出为内环控制器输入的参考量．串级控制系统如图4所示．

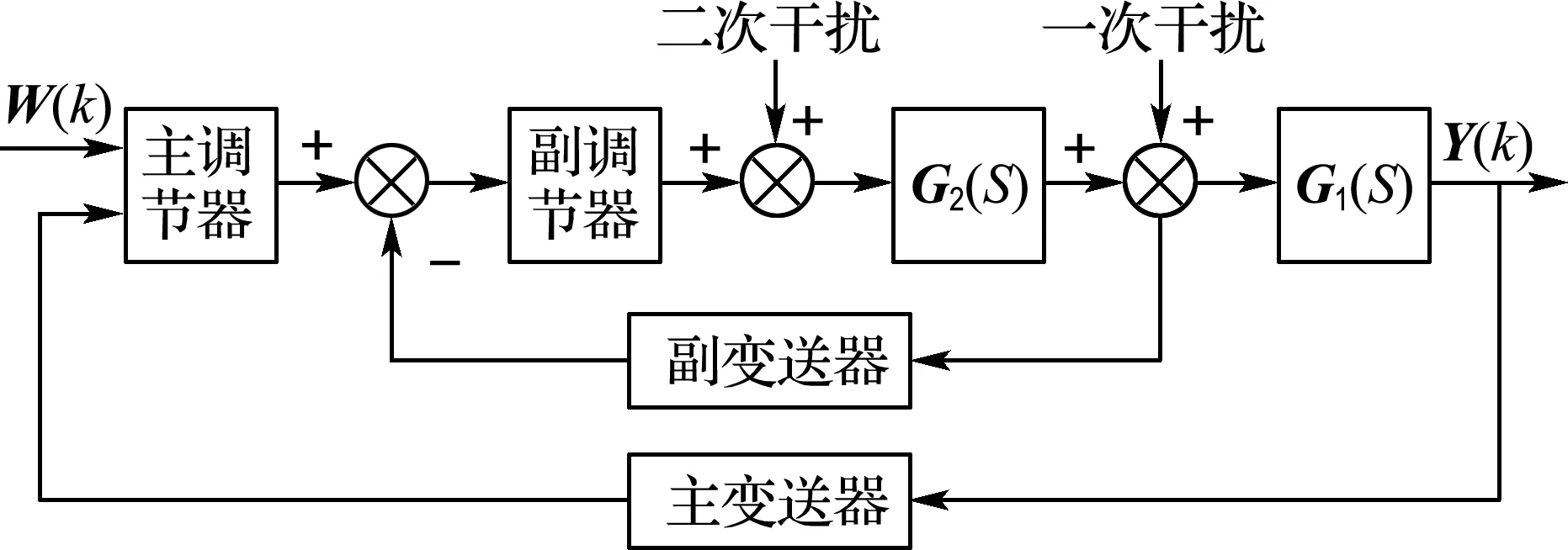
图4 串级控制系统

由控制过程来看，以二级串级控制为例，两个控制器串联工作，协调一致．主调节器根据主参数与给定值的偏差而动作；副调节器根据副参数与给定值的偏差而动作，其给定值为主调节器的输出．与简易控制系统相比较，对于一次干扰项，串级控制的副、主调节器先后进行粗调和细调，极大降低了干扰的影响，提高了控制质量，但同时也为整定参数带来不便．与单回路回馈控制系统比较，串级控制系统有许多优点，如能改善对象的动态特性、提高系统的控制质量，能迅速克服进入随动回路的二次扰动，能提高系统的工作频率，以及对负荷变化的适应性较强，等等．本实验中内环采用PID控制，其输入与输出的关系式为

(10)

其中Kp为比例系数，Ki为积分系数，Kd为微分系数．内环相当于加纯滞后的广义对象，外环是模型预测控制，可以实现纯滞后对象有效控制．

3.2 模型预测控制算法

一般地，模型预测控制由3部分构成，分别为预测模型、滚动优化和反馈校正[7]，如图5所示．

预测模型即描述系统动态特性的模型．预测模型可以是基于非参数式的，例如阶跃响应、脉冲响应模型，还可以是基于参数式的，例如状态方程、传递函数等[8-9]，本实验的预测模型选择基于参数式的状态方程．

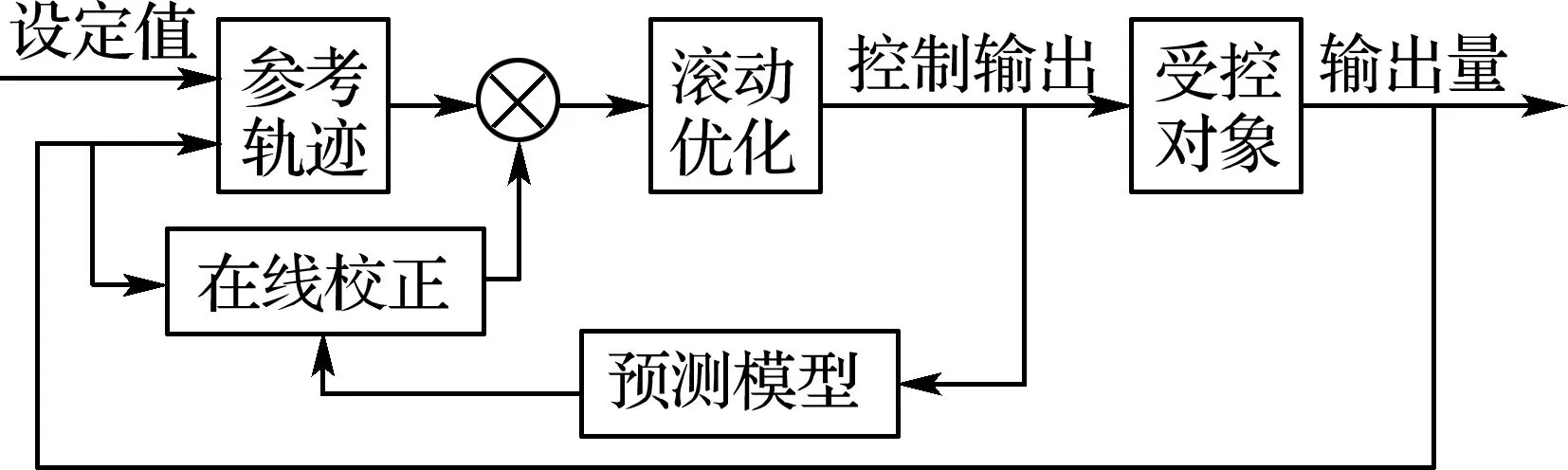
图5 模型预测控制算法流程

与一般最优控制不同，预测控制不是一次将各个时刻最优解都计算好，而是随着采样时刻的前进反复地在线进行，故称为滚动优化．优化性能指标是一种有限时间的优化过程，只从当前采样时刻开始的一个有限区间．在每一时刻得到一组未来的控制动作并只实现本时刻的控制动作，到下一时刻重新预测优化新的控制，每步都是反馈校正，有更强的鲁棒性[10]．

假定控制作用保持不变，在k时刻，未来N个时刻输出的初始预测值为

yi=yO(k+i)；i=1,2,…,N

(11)

在M个连续的Δu(k),…,Δu(k+M-1)控制增量作用时，未来各时刻的输出值为

j-1)；i,j=1,2,…,N

(12)

根据公式，把对象输出的初始值作为已知条件，根据未来控制作用增量即可计算未来的控制输出．M称为控制时域．

在任意k时刻，从该时刻起的M个控制增量都要被确定，使被控对象在未来P个时刻的输出预测值yM(k+i)尽可能地接近给定的期望值ω(k+i)，i=1,2,…,P．预测控制需要通过一个性能指标来确定控制的最优解，并且这个性能指标尽可能地涉及系统未来的行为．一般可以取被控对象的输出在未来各个时刻跟踪期望轨迹的方差最小．性能指标为

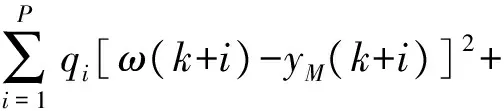
(13)

其中qi和rj分别是误差和控制力的加权系数．选取适当的qi和rj使得目标函数值J最小，此时的控制力即为最优控制力．

利用预测模型式(12)导出性能指标中y与Δu的关系,这一关系可用向量形式写成

yPM(k)=yPO(k)+GΔuM(k)

(14)

(15)

可通过极值必要条件dJ(k)/dΔu(k)=0求得

ΔuM(k)=(GTQG+R)-1GTQ[ωP(k)-yPO(k)]

(16)

取其中的即时控制作用增量Δu(k)构成实际控制

u(k)=u(k-1)+Δu(k)

(17)

到下一时刻,它又提出类似的优化解求出Δu(k+1)，即滚动优化．

在每一个采样时刻，预测控制都可以根据预测值与测量值进行比较，得到预测误差，再基于该误差来校正模型的预测值．校正后的预测值作为依据来计算最优解，形成负反馈，故称为反馈校正．

对象的实际输出为y(k+1)，并把它与模型预测输出yM1(k+1|k)相比较,构成输出误差e(k+1)=y(k+1)-yM1(k+1|k)．

采用对e(k+1)加权的方式修正对未来的预测：

(18)

在k+1时刻,预测的未来时间点将随着时间基准点的变化而变化为k+2,…,k+1+N．

(19)

在已知yPO(k+1)的情况下可经过上文推导过程对k+1时刻进行优化计算，求出Δu(k+1)．

3.3 延时补偿

根据文献提出的时滞补偿理论，对本系统进行时滞补偿．自由度为n，延时量为τ的悬臂梁系统的动力学方程可以表示为

M

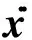
x．．

(t)+C

x．

(t)+Kx(t)=um(t-τ)+f(t)

(20)

其中C是阻尼矩阵，K是刚度矩阵，M是质量矩阵．状态空间方程为

=Ay(t)+Bum(t-τ)+Ef(t)

(21)

经过延时补偿后，可得到

y．(t)=Ay(t)+Bum(t)+Ef(t)

(22)

扩展后的系统矩阵为

(23)

本文中，由于采用无线网络控制系统，不可避免地引入了延时．时滞补偿虽然可以一定程度地弥补时滞带来的问题，但同时也对原有模型进行了改变，不再是不加延时的被控对象，即被控对象的状态空间模型发生了变化[11]．

4 仿真与实验验证

本研究基于Simulink搭建仿真环境，仿真和实验过程分为以下几个步骤进行：首先，根据悬臂梁和压电陶瓷的静态参数，建立悬臂梁模型的状态空间方程；其次，根据模型设计串级控制器并预设一个估计参数；再次，根据仿真结果调整控制器参数直到控制效果和控制力输出达到一个平衡点为止；接着将基于Simulink搭建的控制算法程序编译生成SDF文件并下载到dSPACE控制器中；最后搭建实验系统进行实验测试并验证系统的控制性能．

本实验的仿真阶段采用的是龙格-库塔法来求解微分方程，固定步长为0.001 s．控制器相关参数的整定是本实验的难点之一．本系统采用MPCRQk作为控制模块，其中，P和M不宜设置过大，设置过大会导致输入振幅很小时控制力漂移；R和Q体现为权重的设置，分为控制力权重和振幅的权重．

模型预测控制中P表示对k时刻起未来多少步的系统输出逼近期望值感兴趣．P取小值可以使系统快速稳定到目标状态，但是牺牲了稳定性，易发散；而P取值过大，稳定性得到了加强但是系统很难快速到达目标状态．M表示的是未来控制量增量的个数．P是控制量的增量在预测时域中改变的次数．在P值确定的情况下，控制增量的个数M越大，各个时刻的预测输出与期望值就越接近，这样获得的性能指标就越好．增大(减小)P与减小(增大)M得到的效果差不多．R的引入避免了控制量即Δu的剧烈变化，可以看作优化性能指标中一种软约束．适当的R可以使控制量的变化变小并逐渐趋于平缓．Q反映的是对不同时刻输出逼近期望值的重视程度．

本实验从两个方面对结果进行定量分析，分别为计算到达时间和位移均方根分析，其中到达时间指的是悬臂梁的振动幅度缩小到原来振动幅度的5%时所需要的时间．由于仿真模型会有误差，仅对实际实验数据进行定量分析．

4.1 无延时

首先对不加无线模块时的系统进行仿真，此时信号不经过无线发送和接收，所以认为无延时，图6为仿真结果．图7为用dSPACE对悬臂梁进行实际减振的效果图．经计算，在无延时条件下，无控系统到达时间为16.5 s，有控系统为7.6 s，到达时间缩减了54%；有控系统的位移均方根相比无控系统缩减了33.4%．从图中可以看出，所设计的控制器在无延时情况下减振效果良好．

4.2 控制器前端有延时

对在位移信号进入dSPACE这条路径上加入无线模块进行仿真和实验，此时只在从悬臂梁状态空间模型到控制器设置延时，延时时间设置为25 ms，加入一个滤波器，图8为仿真结果．图9为用dSPACE对悬臂梁进行实际减振的效果图．经计算，在该条件下，无控系统到达时间为16.5 s，有控系统为9.1 s，到达时间缩减了45%；有控系统的位移均方根相比无控系统缩减了26.5%．

图6 无延时仿真结果

图7 悬臂梁无延时位移时程图

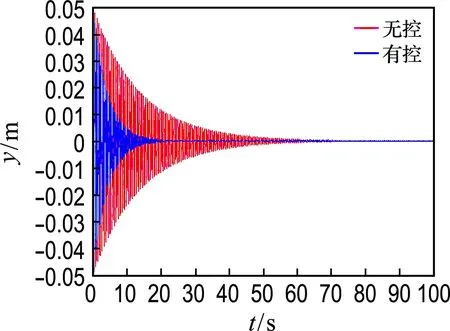
图8 控制器输入端有延时的仿真结果

图9 控制器输入端有延时的实验结果

4.3 控制器前后端都有延时

前面实验表明在信号采集端设置无线装置存在延时的情况下仍然可以通过调节控制器参数进行悬臂梁振幅的减振，现在控制器前后均设置无线模块，进行仿真和实验．图10为仿真结果．图11为用dSPACE对悬臂梁进行实际减振的效果图．经计算，在该条件下，无控系统到达时间为16.5 s，有控系统为10.1 s，到达时间缩减了39%；有控系统的位移均方根相比无控系统缩减了24.5%．

图10 控制器输入、输出端有延时的仿真结果

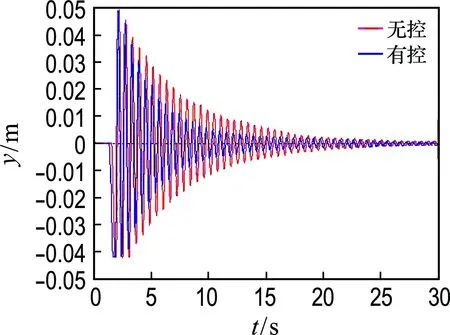
图11 控制器输入、输出端有延时的实验结果

5 结论及展望

(1)在无线控制有延时的情况下，经过延时补偿后，本文提出的串级控制器能实现对悬臂梁结构的减振．

(2)由于实验中存在的未知干扰以及噪声等问题，且建模属于简化模型，仿真得到的控制效果要优于实验对应的控制效果．

(3)本文提出的控制算法对于控制器前后均有延时的工况仍具有较好的控制效果．

(4)本文只讨论了针对本实验所用到的无线模块的固定延时进行的延时补偿，当无线控制中出现大延时或不确定延时时也会对控制效果产生影响，需要进行研究．

(5)因为延时的存在，梁的自振频率越大，振动周期越小，就要求延时越小，否则很难有较好的控制效果．怎样进一步缩小延时并应用于高频振动控制需要进一步研究．

在实际工程分析中，悬臂梁是比较典型的简化模型，大部分实际工程受力部件都可以简化为悬臂梁模型．本文以悬臂梁为研究对象对提出的算法进行验证，以便今后在桥梁等复杂钢结构工程领域进行应用和推广．

[1] 喻 言,欧进萍. 海洋平台结构振动监测的无线传感实验研究[J]. 哈尔滨工业大学学报, 2007,39(2):187-190.

YU Yan, OU Jinping. Wireless sensing experiments for structural vibration monitoring of offshore platform [J].JournalofHarbinInstituteofTechnology, 2007,39(2):187-190. (in Chinese)

[2] 赵永春,季宏丽,裘进浩,等. 基于压电元件的悬臂梁半主动振动控制研究[J]. 振动、测试与诊断, 2009,29(4):424-429.

ZHAO Yongchun, JI Hongli, QIU Jinhao,etal. Semi-active vibration control of cantilever beam using piezoelectric element [J].JournalofVibration,Measurement&Diagnosis, 2009,29(4):424-429. (in Chinese)

[3] 朱秋琴,黄云龙. 非线性广义预测控制算法及其仿真研究[J]. 机电工程, 2008,25(11):101-104.

ZHU Qiuqin, HUANG Yunlong. Nonlinearal general predictive control algorithm and simulation [J].Mechanical&ElectricalEngineeringMagazine, 2008,25(11):101-104. (in Chinese)

[4] 邵惠鹤,任正云. 预测PID控制算法的基本原理及研究现状[J]. 世界仪表与自动化, 2004,8(6):17-21.

SHAO Huihe, REN Zhengyun. The basic principle and research status of predictive PID control algorithm [J].InternationalInstrumentation&Automation, 2004,8(6):17-21. (in Chinese)

[5] 王国玉,韩 璞,王东风,等. PFC-PID串级控制在主汽温控制系统中的应用研究[J]. 中国电机工程学报, 2002,22(12):50-55.

WANG Guoyu, HAN Pu, WANG Dongfeng,etal. Studies and applications of PFC-PID cascade control strategy in main steam temperature control system [J].ProceedingsoftheCSEE, 2002,22(12):50-55. (in Chinese)

[6] 孙 璇. 串级控制系统的几种典型应用[J]. 科技资讯, 2007(2):18.

SUN Xuan. Application of several typical cascade control system [J].Science&TechnologyInformation, 2007(2):18. (in Chinese)

[7] 刘 钢,李圣怡,范大鹏. 机电伺服系统的预测函数控制算法研究[J]. 国防科技大学学报, 2004,26(2):89-93.

LIU Gang, LI Shengyi, FAN Dapeng. Studies of predictive functional control arithmetic in electromechanical servo system [J].JournalofNationalUniversityofDefenseTechnology, 2004,26(2):89-93. (in Chinese)

[8] 余世明. 预测控制算法及其应用研究[D]. 杭州:浙江大学, 2001.

YU Shiming. Predictive control algorithm and its application [D]. Hangzhou:Zhejiang University, 2001. (in Chinese)

[9] 齐维贵,朱学莉,丁 宝. 动态矩阵控制的模型简化与预报误差校正[J]. 电子学报, 2004,32(7):1206-1208.

QI Weigui, ZHU Xueli, DING Bao. Model simplification and prediction error correction of dynamic matrix control [J].ActaElectronicaSinica, 2004,32(7):1206-1208. (in Chinese)

[10] 秦 辉. 预测控制集结优化策略的研究及仿真分析[D]. 上海:上海交通大学, 2006.

QIN Hui. Researches and simulations of aggregation optimization strategy in predictive control [D]. Shanghai:Shanghai Jiao Tong University, 2006. (in Chinese)

[11] YU Yan, GUO Jinhe, LI Luyu,etal. Experimental study of wireless structural vibration control considering different time delays [J].SmartMaterialsandStructures, 2015,24(4):045005.

Studyandvalidationofcascadewirelesspredictivecontrolalgorithmforcantileverbeamstructure

YANGChangping1,YUYan*1,2,LILuyu3,LENGXiaozhi1,ZHANGShuaishuai1,OUJinping3

(1.FacultyofElectronicInformationandElectricalEngineering,DalianUniversityofTechnology,Dalian116024,China；2.KeyLaboratoryofLiaoningforIntegratedCircuitsTechnology,Dalian116024,China；3.SchoolofCivilEngineering,DalianUniversityofTechnology,Dalian116024,China)

The application of structure active control based on a wireless method has been studied preliminarily and tends to replace the traditional wired control method. However, the problem of time delay in a wireless control system is inevitable, and because of this problem, system stability and control capability are greatly influenced. Therefore, it is indispensable to solve the problem of time delay in a wireless control system. Based on a cantilever beam, a wireless control experimental system is proposed and implemented, and by using a cascade control strategy with a time delay compensation algorithm which combines PID and model predictive control, simulation and experiment are carried out in three different conditions which are activated without delay, with time delay at the signal acquisition terminal, with time delay at both acquisition terminal and output terminal respectively. Simulation and experiment results demonstrate that this method can effectively compensate for time delay and enable the wireless control system to exhibit excellent control performance that can be favorably compared with that of wired control. It has a good reference for practical engineering applications.

time delay compensation; wireless control; cantilever beam; predictive control

1000-8608(2017)06-0650-07

TP212；TP273；TU323.3

A

10.7511/dllgxb201706015

2017-02-15；

2017-09-23．

国家自然科学基金资助项目(51678108,51378093)；国家国际科技合作专项项目(2015DFG82080)；辽宁省高校优秀人才支持计划资助项目(LJQ2015028)；辽宁百千万人才工程项目(201724).

杨常平(1992-)，男，硕士生，E-mail:ychp100@mail.dlut.edu.cn；喻 言*(1977-)，男，教授，E-mail:yuyan@dlut.edu.cn.