考虑不确定性因素的有限元屈曲模型验证

聂小华 吴存利

(中国飞机强度研究所，西安710065)

考虑不确定性因素的有限元屈曲模型验证

聂小华 吴存利1)

(中国飞机强度研究所，西安710065)

研究了考虑不确定性因素的有限元屈曲模型验证和确认方法，提出了不确定参数选择的相关性和敏度分析方法以及基于面积度量的模型评估方法.针对化铣整体壁板，开展了有限元屈曲模型验证研究，首先利用8件试验件，获得了壁板屈曲载荷的试验值，然后依据试验加载情况，建立了考虑试验台的壁板有限元模型，最后利用面积度量方法对有限元模型进行了验证和确认.本文的模型验证和确认方法可为其他工程结构开展类似的工作提供借鉴.

整体壁板,建模,模型验证,不确定性,正态分布,面积度量

有限元仿真模型的验证一直是工程技术人员感兴趣的问题.近年来随着虚拟试验技术的发展和在工程中成功应用，有限元模型验证更引起人们广泛的关注. 一方面通过模型验证保证虚拟试验结果对物理系统或物理过程相关特性的定量估算是可靠的；另一方面为模型修正提供指导.关于模型验证，最初主要集中在确定性结构或系统，利用物理试验数据对有限元模型进行验证和确认，然而，工程结构中通常包含各种不确定性因素，如不同批次材料的弹性模量、密度参数，结构制造和工艺引起的几何尺寸允差，结构的装配允差，试验中测量允差等,因而工程计算中所涉及的物理参数都具有某种程度上的不确定性.由于这些不确定性因素的存在，结构响应预测变得更为复杂.为了使建立的有限元模型更符合工程实际，利用试验数据对有限元模型验证就应充分考虑结构中各个不确定性因素，以及结构物理试验中的不确定因素.

目前，对于考虑不确定性因素的模型验证，国外已开展了大量研究，发展了多种模型验证方法.Ferson等[1]针对热分析模型,提出了累积函数面积度量方法来验证热分析模型，Thacker等[2]系统讨论了累积函数面积度量的方法，并介绍了Z度量的方法，Hills等[3]详细研究了基于最大概似度量的模型验证与评估方法，并讨论了与其他度量方法的等效性,McFarlan等[4]研究了采用多响应量对模型验证，并诠释了采用多元统计的Hotelling’s T2检验来验证模型,Roy等[5]从不确定参数来源、不确定参数结构及传播、模型验证等方面进行了全面概述，并通过具体事例进行了说明.近年来随着模型验证技术的发展，国外又出版了这方面的专著[68]，制定了模型校核和验证指南[910].对于考虑不确定性因素的模型验证和确认，国内也开展了相应的研究工作，主要集中在结构动力模型[1112]，而对于静力有限元模型，目前还未见有公开的资料.

本文研究了考虑不确定性因素的静力有限元模型的验证方法，讨论了模型验证和确认方法，包括模型不确定性参数选取的敏度分析方法，以及基于面积度量的模型验证方法.针对化铣整体壁板，开展了模型验证研究.首先通过 8件壁板试验件，获得了壁板整体失稳载荷的试验结果，然后依据试验支持和加载方式，建立了化铣整体壁板有限元模型，最后利用面积度量方法完成了对有限元模型的验证和确认.

1 考虑不确定因素的模型验证方法

1.1 相关性和敏度分析

考虑不确定性因素的模型验证，首先需要选择不确定性参数，实际结构含不确定性参数较多，这种不确定性包括几何、材料、载荷、边界条件，每一类不确定性对预测结果可能都有影响，为了寻找对预测结果影响较大的参数，需要进行相关性和敏度分析.

对多变量系统，传统的敏度分析采用只变化一个参数，其他参数取恒定值的策略.这种方法得到的敏度值是一个局部值，不能衡量参数在整个取值范围内对系统响应的影响.本文对不确定性参数相关性和敏度分析，采用随机分析方法，其过程如下.

假设有n个随机参数，第i个随机参数的均值和标准差为µi和σi,其第j个样本可以表示为

式中，xij表示对第i个随机参数的第j次抽样，fi为第i个随机参数的概率密度函数,Rand[fi(µi,σi)]j表示对服从概率密度函数为fi的随机变量第j次随机抽样.

对n个随机参数分别进行m次抽样，得到每个随机参数的m个样本，利用样本通过模型计算，得到结构响应值的m个样本，即

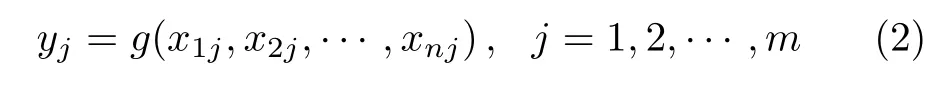
获得了随机参数样本和模型预测值的样本，就可以利用统计方法分析随机变量对模型预测值的相关性和敏度.相关性采用 Spearman秩系数[13]来度量.Spearman秩系数是用来考察分析参数在取值范围内的变化对输出量的影响.第i个随机参数与模型预测值的Spearman秩系数可写为

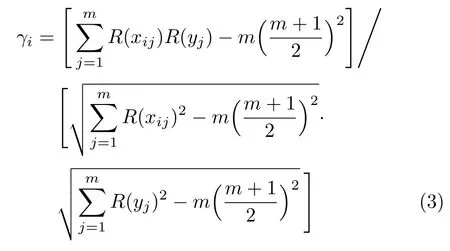
式中，xij和yj为输入变量和响应输出变量，R(xij)和R(yj)为xij和yj在其样本序列中的秩.

实际上Spearman秩系数是输入和输出参数之间相互关系的非线性度量，用于度量变量之间相互关系的强弱，在没有重复数据的情况下，如果一个参数随另一个参数的变化是严格单调的，则Spearman秩系数就是1或−1.系数为1意味着输入参数和响应值为正相关，而−1为负相关.在计算样本秩时，如果某几个样本相同，则这些样本的秩取其平均值.

响应量对输入参数的敏度可以采用最小二乘法得到，第i个参数与响应量的相关系数是

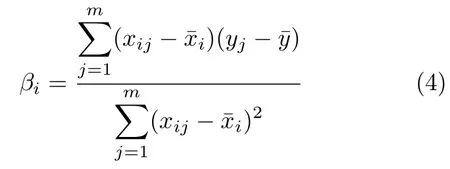
式中,xij和yj分别为输入变量和响应输出变量，¯xi为xij的均值，¯y为yj的均值.

由式(4)计算的敏度值的大小与输入参数的量级有关，比如材料的杨氏模量为100GPa，而泊松比为0.1，为了消除参数量级对敏度大小的影响，采用折算敏度量，即

相关性和敏度分析指明了模型对输入参数的依赖性.它可以用来指导对模型不确定参数的选择，数学模型对参数的依赖性也指明了物理系统对参数的依赖性.

1.2 模型验证方法

对模型验证，工程中通常采用4种方法：(1)假设检验；(2)贝叶斯方法；(3)均值比较；(4)面积度量方法.前3种方法都有其固有的缺点.例如假设检验先对所研究的问题作假设，然后根据某统计量的值，以及给定的显著性水平进行检验，作出拒绝或接受的判断，这与模型验证有显著区别，模型验证是定量评估模型的精度.贝叶斯方法多用来对模型修正，而均值比较也只能是模型预测值和试验值集中趋势的比较，不能定量评估模型好坏.实际上，预测值概率分布包含了大量模型信息，利用预测值和试验值的概率密度分布函数或累积分布函数来客观地度量有限元模型逼近数学模型的程度是恰当的，于是面积度量方法被提出了[1]，并被进一步得到诠释[10].

面积度量方法定义如下

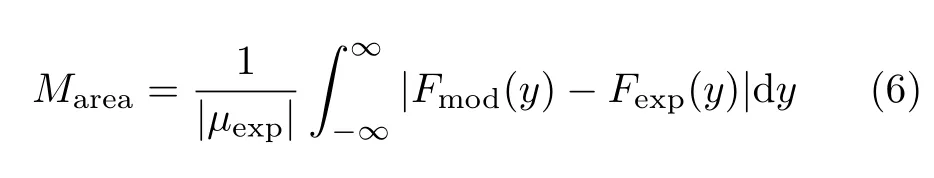
式中，Fmod(y)和Fexp(y)分别是模型预测值和试验值的累积分布函数，µexp为试验值的均值.上式积分的含义是模型预测结果与试验结果累积分布函数曲线所围成的面积，其值越小，表明模型越能模拟实际物理结构.

从式(6)可以看出，面积度量非负.如果模型预测值和试验值的累积函数完全相同，面积度量值为零.对于模型确认的阈值，文献 [10]建议 M阈值为0.1，即如果Marea≤0.1，模型通过验证，即认为模型是合理的，否则模型不被认可.

2 化铣整体壁板屈曲有限元模型验证

2.1 试验研究

化铣整体壁板共 8件.试验件构型见图 1,其中试验件高度为典型的翼肋间距，未考虑蒙皮的曲率，试验件高 h=300mm,蒙皮厚度 t=3mm,筋条间距 l=70mm,左右端加筋条距侧边距离都为l1=35mm.

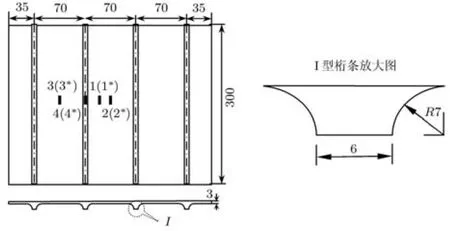
图1 试验件构型及尺寸

试件在25吨材料试验机上进行端压，材料试验机的载荷精度为±1%.用千分表和位移传感器测量试件的端部压缩量和蒙皮、长桁的挠度.用YJD-1应变仪测量蒙皮，长桁的纵向压缩和弯曲应变.试验装置见图2.

图2 试验装置

试件置于压力机上、下两台面之间，采取平端压方法.安装时试件横剖面形心对准压力机压力中心，并保证试件轴线与压力机台面垂直，试件两端面与压力机台面贴合且平行.为了确定试件受载时的应力水平与临界屈曲载荷，试件上贴有应变片(见图1)，试件端部位移用百分表来测量.试验时，先进行预试，加载至估算载荷的30%，进行应变、位移测量，分析试验情况.在试件状态满足试验要求的情况下，进行正式试验，分级加载，进行应变、位移测量和变形观察，直至试件失稳破坏为止，记录失稳载荷.

从试验中观测到8件试验件均因整体失稳而导致破坏，破坏前蒙皮无明显局部失稳波形，高载时，壁板呈柱状弯曲，突然总体破坏.

图3给出了试验应变随载荷的变化图.从图3可见，试验件前后面相同位置的应变(1对1∗，2对2∗，3 对 3∗，4 对 4∗)以及左右应变 (1∗，2∗对 3∗，4∗)的测量值存在着明显的差异，这是由壁板的初曲度，端面与试验机台面不垂直导致压力不均匀造成的.

表1为试验件屈曲载荷的试验值.试验结果较为分散，其原因大致有：(1)8件试验件材料来自不同批次的材料，材料差异性引起试验结果差异；(2)工艺引起化铣厚度差异；(3)压力不均匀.

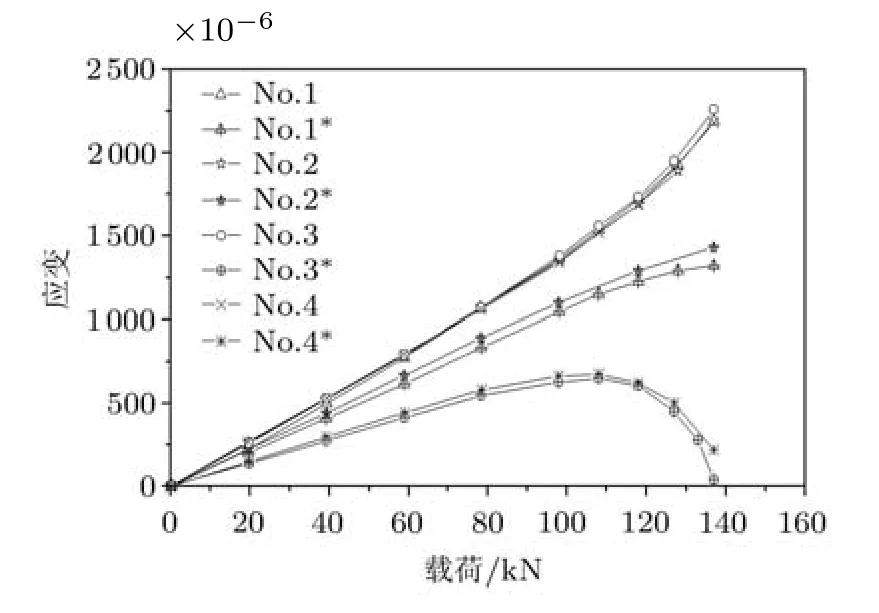
图3 试验应变

表1 化铣整体壁板试验结果

2.2 有限元建模研究

对化铣整体壁板屈曲载荷分析，首先需要建立有限元模型.由于屈曲载荷与模型的边界条件、网格密度和单元选择有关，因此建模时重点考虑载荷施加、边界约束和网格划分和单元选取等因素.

2.2.1 载荷施加

载荷施加要考虑两方面因素，一方面需要合理地模拟试验加载的平端压方法，另一方面要考虑试验件端头的不平度对载荷分配的影响.为了能真实地模拟试验加载情况，对压力机台面的部分结构也建立有限元模型，并在模型的上方选取两个点作为载荷加载点，这两个点应在同一个水平面上，且分别应在二分之一试验件形心延长线上，利用多点约束建立加载点和上台面的刚体约束.图4为载荷施加示意图.

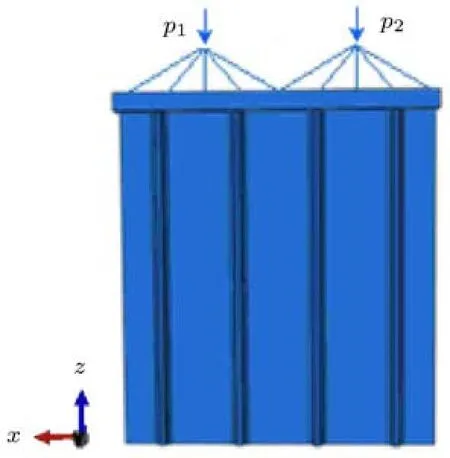
图4 载荷施加示意图

如果施加的总载荷为 p，则作用在两个加载点上的载荷为

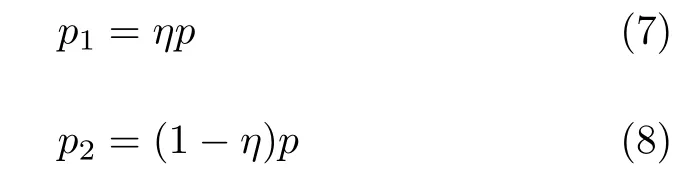
式(7)和式(8)中，η为载荷分配系数，η取0.5时，模拟载荷均匀加载；η取其他值，模拟载荷不均匀加载.

2.2.2 边界约束

边界约束施加也应模拟试验件真实支持情况，由于试验时采用平端压方法，压力机台面和试验件端面只有z的负方向运动，因此，对试验件和压力机台面施加约束如下.将试验件上端头的加筋和蒙皮内侧边固定在压力机上台面，对压力机台面施加x向和y向的约束.对于试验件下端面，约束端面上所有z向位移、蒙皮内侧边y向位移和形心点的x位移.这里只对端头蒙皮的内侧边施加y向约束，其目的是释放蒙皮端面的面外变形.

2.2.3 材料属性

由于试验件在材料线性范围内发生整体屈曲，因此有限元建模时只考虑材料的线性特性.试验件材料为Ly12cz，取其弹性模量E为75.362GPa，泊松比µ为0.291.压力机台面为30CrMnSiNi2A钢，材料弹性模量为196GPa，泊松比为0.3.

2.2.4网格划分和单元选择

在结构屈曲分析计算中，网格的尺度显著影响着计算结果的精度.Lynch系统地研究了机身加筋板离散化为曲壳元时，单元尺度对解的收敛性的影响[14].研究表明解的收敛性对网格尺度的要求跟元素类型有密切关系.对化铣整体壁板建模，采用实体单元.下面利用已有理论解的四边简支板来确定厚度方向划分为一个单元时，利用商用Abaqus软件来研究其他方向单元尺度对解的收敛性的影响.

取试验件1/4蒙皮来研究线性元(C3D8R)和二次元(C3D20R)的尺度对屈曲载荷的影响.图5为四边简支蒙皮示意图，图6为计算结果.从图 6可知，随着蒙皮长度和宽度方向单元数增加，采用两种单元的计算结果都收敛到解析解.对于C3D20R元素，采用较粗的网格就能收敛到理论解.因此对整体壁板蒙皮建模，采用C3D20R元.

图5 1/4蒙皮

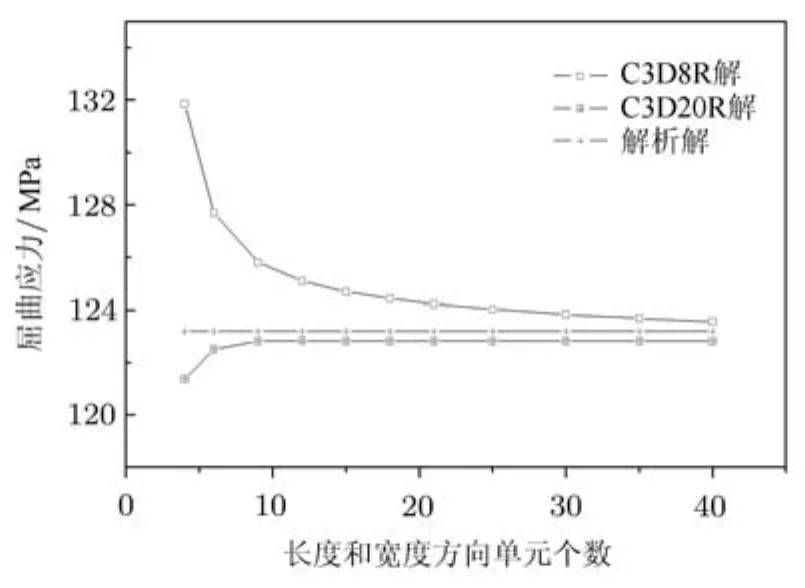
图6 单元个数对计算结果影响

采用Abaqus软件前置界面对整体壁板建模，将筋条和蒙皮分开来建，然后利用 tie命令将筋条和蒙皮绑在一起.为了获得较高精度的计算结果，蒙皮划分为40×40×1网格.筋条也采用C3D20R元模拟，为了不造成单元形状的畸变，对筋条剖面划分时忽略了尖角，见图7，将剖面划分8份，见图8，在长度方向划分为40个单元.

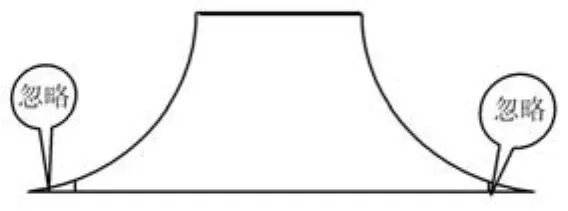
图7 筋条简化

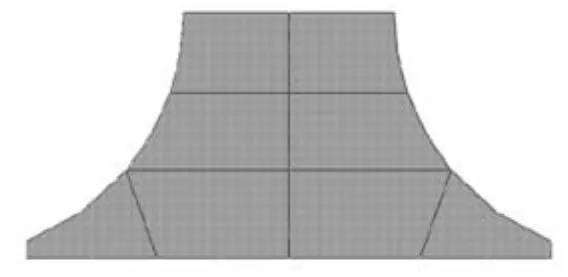
图8 筋条剖面划分

对于与整体壁板连接的压力机结构，采用C3D8R体元来离散化. 整个模型共有 1632个C3D20R单元，240个 C3D8R单元.试验件与连接结构的有限元模型见图9.

图9 整体壁板与连接结构有限元模型

2.3 模型验证

模型验证是通过度量计算结果与试验结果一致性来实现的.利用已有的试验数据，通过统计方法来验证有限模型，在模型验证中充分考虑试验和建模中一些不确定因素.这些不确定因素包括测量误差、设计允差、制造允差等.为了有效地对模型评估，首先需要分析试验和模型中一些不确定量对预测结果的相关性及敏度，采用式(3)的Spearman秩方法和式(4)的最下二乘方法来研究屈曲载荷对不确定参数的相关性和敏度，然后利用式(6)的面积度量方法对模型验证.

2.3.1 不确定参数对屈曲载荷相关性和敏度

不确定参数主要包括载荷系数η、板的厚度t、筋条宽度b、材料的弹性模量E和泊松比ν，工程分析中认为这些随机参数服从正态分布.表2依据工程经验给出这些随机量的均值、变异系数、标准差以及取值区域.

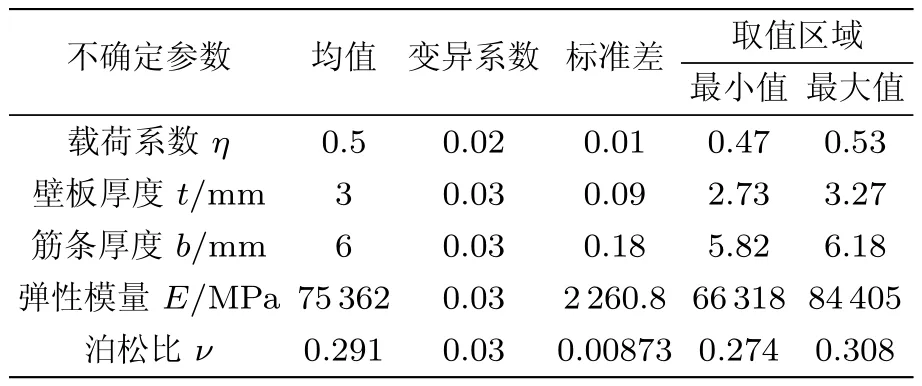
表2 随机变量统计性质和取值范围

采用300组随机参数样本进行分析，每个随机参数的样本可通过蒙特卡洛方法抽样得到.由于这些参数都认为服从正态分布，在实际操作中,只要知道均值u和标准差σ，就可利用函数Random.gauss(u,σ)随机产生服从均值为u和标准差为σ的样本.图10给出了屈曲载荷随不均匀载荷系数、结构几何参数和材料性能的变化关系.图中的均值线的斜率可以看作是屈曲载荷对每个变量的敏度.表3也给出了这些随机参数对屈曲载荷相关性系数和敏度值.从表3和图10可以看出，相对于载荷系数和材料泊松比，板的厚度、筋条宽度和材料的弹性模量对屈曲载荷具有较大的相关性和敏度，这说明整体壁板的屈曲载荷对这些参数有较大的依赖性.因此，对模型验证，只考虑板的厚度、筋条宽度和材料的弹性模量的不确定性.

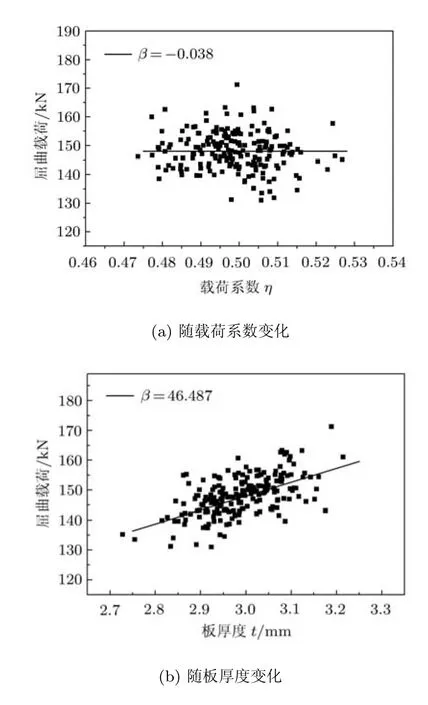
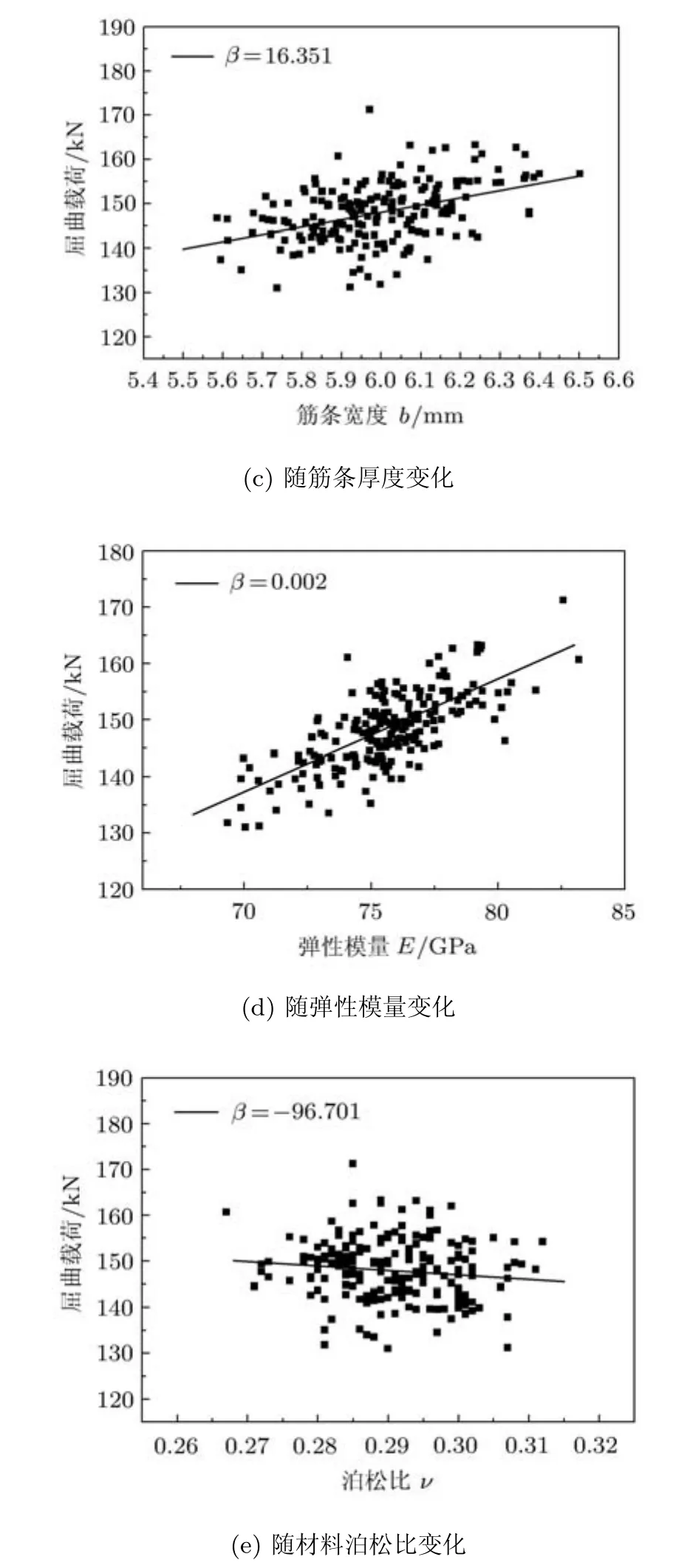
图10 屈曲载荷对各随机量的敏度

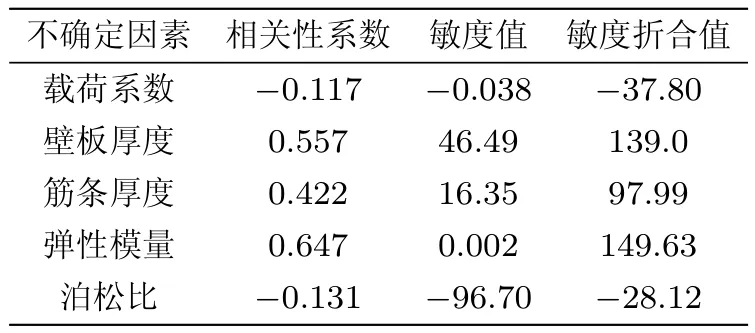
表3 随机变量的相关性和敏度

2.3.2 考虑不确定性因素的有限元模型验证

对模型验证，需要知道模型预测值和试验值的累积分布函数 (cumulative distribution function,CDF)，然后利用式(6)来计算二者围成的面积，再计算 Marea，如果 Marea≤0.1，可认为模型是合理的，即认为模型能反映试验件真实刚度以及支持状态.

(1)模型预测值的累积分布函数

由于压力不均匀性以及材料泊松比的不确定性对整体加筋板屈曲载荷影响甚微，在模型验证中，只考虑材料的弹性模量、板的厚度、筋条宽度作为结构的随机参数，3个随机参数的统计特性由表2给出.利用Random.gauss函数获得这3个随机变量的样本，将每组样本代入到参数化的有限元模型中，通过计算获得试验件整体屈曲载荷预测值.

选取400组样本进行随机有限元计算，获得400个壁板整体屈曲载荷样本值.将样本值从小到大分成20个区间，每个区间间距为2kN，计算落在每个区间载荷的频数，得到屈曲载荷与各区间频数图，见图11.

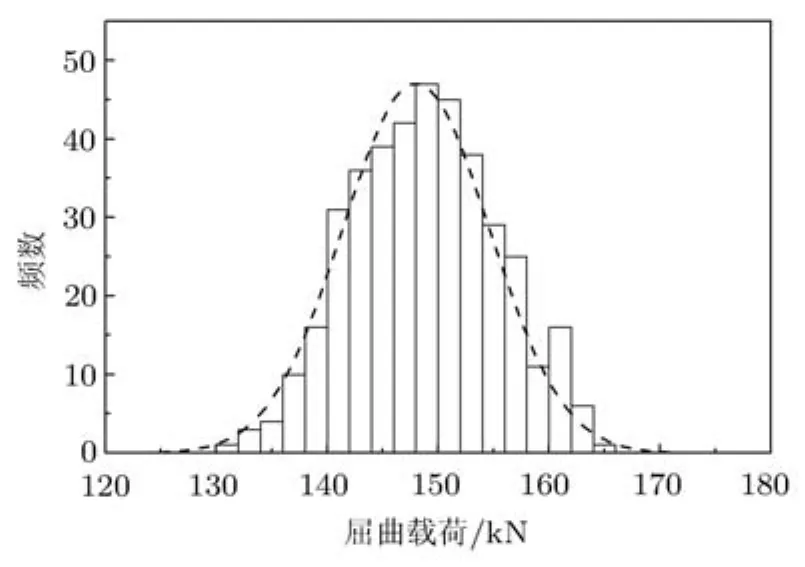
图11 屈曲载荷的柱状分布图

图11显示，在板的厚度、筋条宽度和材料的弹性模量服从正态分布的情况下，加筋板的整体屈曲载荷也服从正态分布.因此，可认为模型预测值累积函数为正态累积函数.

(2)试验值的累积分布函数

试验值的统计分布采用两种方法给出.一种方法是将化铣整体壁板试验结果视为服从高斯分布.利用表 1的 8个试验值，计算高斯分布的均值和标准差.另一种方法是，构造非减的阶梯函数Sn(x)为试验值累积分布函数[1]，Sn(x)表达式为

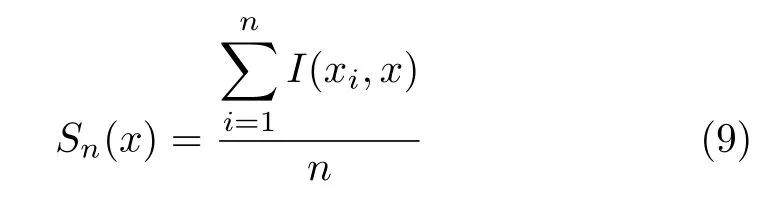
式中，n为试验值样本总数，而I(xi,x)为

实际上，在构造Sn(x)时，假设了每次试验值的概率为1/n,也意外着Sn(x)每次在纵轴上升幅度为1/n.由两种方法给出的试验累积分布函数见图12.

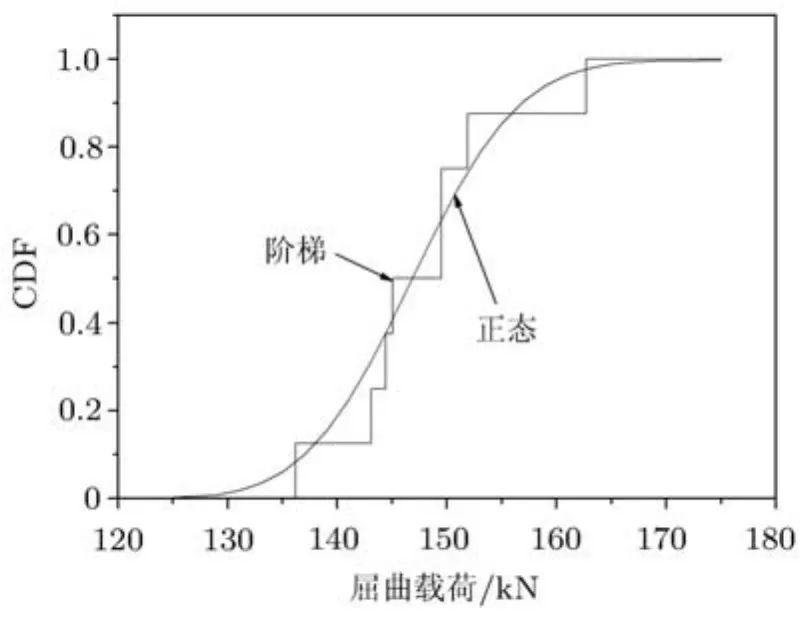
图12 两种方法给出的试验累积分布函数

(3)模型验证和确认

通过计算模型预测值和试验结果的累积分布函数围成的面积实现对模型评估和确认，如图 13所示. 图 13(a)是假定试验值累积分布函数为高斯的情况，而图 13(b)为阶梯分布的情况. 对于图13(a),计算得到面积度量值为Marea=0.006；对于图 13(b)，计算得到 Marea=0.011.M阈值取 0.1，显然Marea＜M阈值，表明本文的屈曲分析模型是合理的.

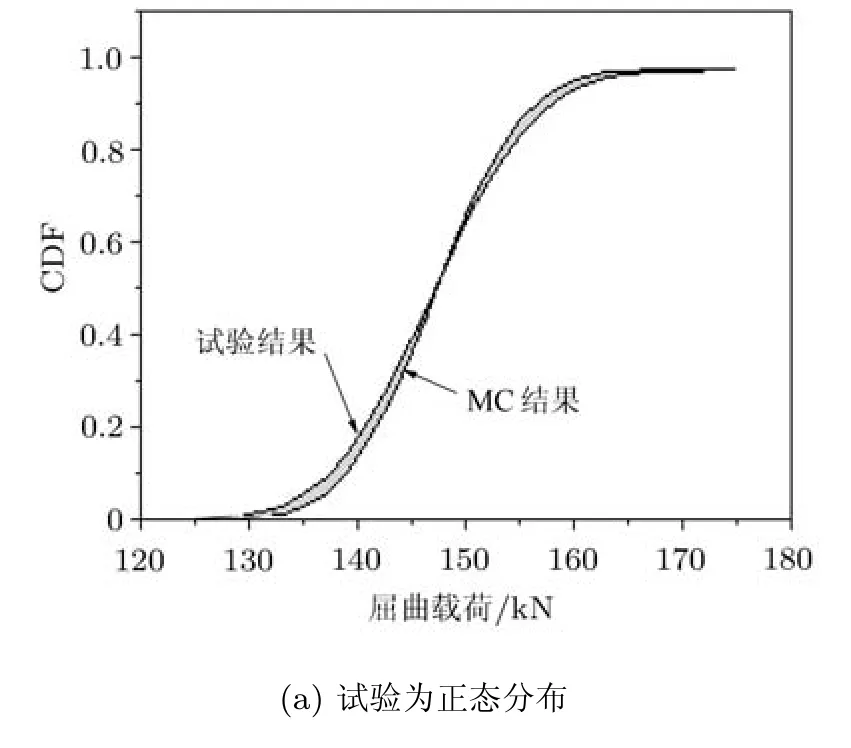
图13 试验和预测的CDF及其所围的面积

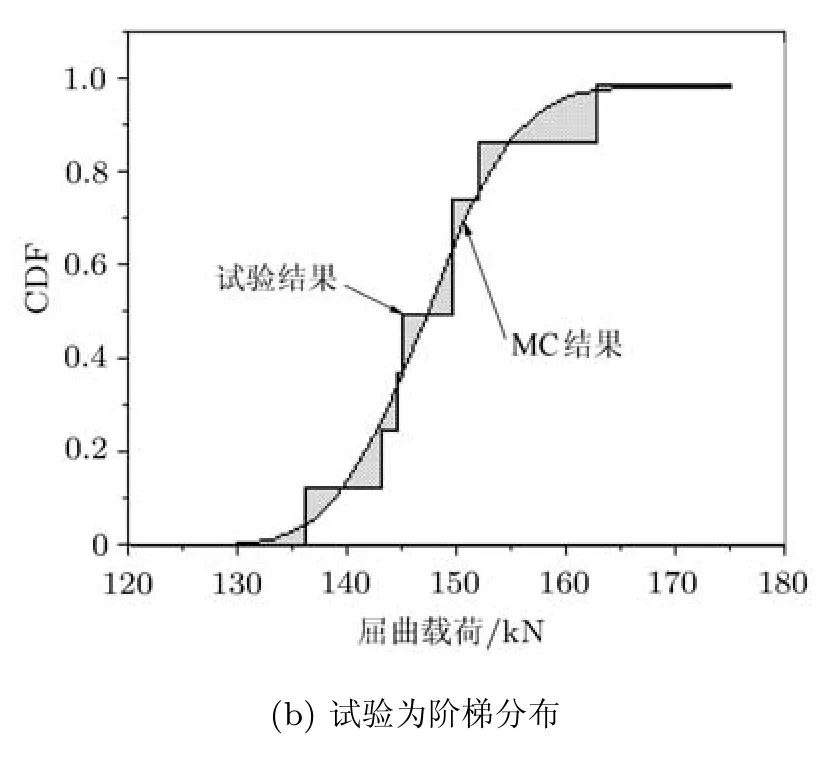
图13 试验和预测的CDF及其所围的面积(续)

3 结论

本文详细研究了考虑不确定因素的有限元屈曲模型验证技术，讨论了不确定参数选取的相关性分析和敏度分析方法，以及基于面积度量的模型验证方法.以整体加筋板为例说明了模型验证和确认的过程.纵观全文，可以得到如下结论.

(1)文中提出的考虑不确定因素的有限元模型验证方法，可以有效地对静力有限元模型进行确认.模型验证中充分考虑了建模过程和物理试验中的一些不确定因素，借用概率统计方法对模型的可靠性进行评价，避免因不确定因素干扰对模型可靠与否作出错误的判断.

(2)不确定参数的选择可采用相关性分析或敏度分析来实现.利用相关性或敏度分析，选取对模型预测结果影响较大的参数，而剔除影响小的参数.

(3)面积度量方法可以有效地对模型进行评估，通过模型预测值和试验值的累积分布函数实现对模型的验证.

考虑不确定因素的模型验证技术需要大量的试验数据，以及多次重复的有限元建模工作，因此需要建立试验数据库，并开展参数化建模的研究.另外，面积度量方法是利用单响应预测值模型进行评估，还不能用于多响应预测值，因此需要发展多响应预测值模型评估技术.

1 Ferson S,Oberkampf WL,Ginzburg L.Model validation and predictive capability for the thermal challenge problem.Computer Methods in Applied Mechanics and Engineering,2008,197(29-32):2408-2430

2 Thacker BH,Paez TL.A simple probabilistic validation metric for the comparison of uncertain model and test results.16th AIAA Non-Deterministic Approaches Conference,Maryland,2014

3 Hills RG,Trucano TG.Statistical validation of engineering and scientific models:a maximum likelihood based metric.Sandia report,SAND2001-1783

4 McFarland J,Mahadevan S.Multivariate significance testing and model calibration under uncertainty.Computer Methods in Applied Mechanics and Engineering,2008,197(29-32):2467-2479

5 Roy CJ,Oberkampf WL.A comprehensive framework for verification,validation and uncertainty quantification in scientific computing.Computer Methods in Applied Mechanics and Engineering,2011,200(25-28):2131-2144

6 Oberkampf WL,Roy C.Verification and Validation in Scientific Computing.Cambridge,UK:Cambridge University Press,2010

7 Roach P.Verification and Validation in Computational Science and Engineering.Albuquerque,N M:Hermosa Press,1998

8 Simmermacher T,Moaveni B,Cogan S,et al.Topics in model validation and uncertainty quantification.The 31st IMAC,Bethel,CT,USA,2013

9 ASME.Guide for verifivationamp;validation in computational solid mechanics，ASME Vamp;V 10-2006，The American Society of Mechanical Engineers,New York，2006

10 ASME.An illustration of the concepts of verification and validation in computational solid mechanics,ASME Vamp;V 10.1-2012,The American Society of Mechanical Engineers,New York，2012

11 陈学前，肖世富，刘信恩.不确定性因素结构的有限元建模与确认.噪声与振动控制,2013,33(5):26-29

12 陈学前，肖世富，刘信恩等.根部柔性梁的不确定性建模与确认，力学与实践,2012,34(1):52-56

13 Spearman C.Demonstration of formulae for true measurement of correlation.Am J Psychol,1907,18:161-169

14 Lynch CJ，Murphy A，Price M，et al.The computational post buckling analysis of fuselage stiffened panels loaded in compression.Thin-walled Structures,2004,42:1445-1464

VALIDATION AND CONFIRMATION OF STATIC FINITE ELEMENT MODEL BY CONSIDERING UNCERTAINTIES

NIE Xiaohua WU Cunli1)
(Aircraft Strength Research Institute of China，Xi’an 710065，China)

The finite element static models are validated by considering uncertain factors.The concepts of the correlation and the sensitivity in selecting uncertain parameters are proposed,as well as a general area metric,to validate finite element models.The model of an integrated stiffened panel is used to demonstrate the validation approach.The physical tests of the integrated stiffened panels are carried out to obtain the buckling loads.The finite element model is built with consideration of the stiffened panel and the test-bed.The reliability of the model is assessed against the experimental data by using the area metric.The validation approach in this paper can be used for similar engineering cases.

integrated stiffened panels,modeling,model validation,uncertainty,normal distribution,area metric

V258.3

A

10.6052/1000-0879-17-047

2017-02-15收到第1稿，2017-03-16收到修改稿.

1)吴存利，研究员，博士，主要从事计算结构力学和飞机强度计算技术的研究.E-mail:cunli888@sina.com

聂小华,吴存利.考虑不确定性因素的有限元屈曲模型验证.力学与实践,2017,39(5):460-467 Nie Xiaohua,Wu Cunli.Validation and con fi rmation of static finite element model by considering uncertainties.Mechanics in Engineering,2017,39(5):460-467

(责任编辑:周冬冬)