二次Riccati方程研究综述①

刘玉堂 辛祥鹏

(聊城大学 数学科学学院, 山东 聊城 252059)

二次Riccati方程研究综述①

刘玉堂 辛祥鹏

(聊城大学 数学科学学院, 山东 聊城 252059)

本文首先介绍了Riccati方程的基本情况，包括研究的部分成果和重要意义. 然后按国内和国际两类文献陈述了从2014年至今Riccaiti方程的研究进展. 对这两类文献又从方程本身的性质、可积性、精确解、数值解、定性理论和Riccati方程的应用等角度分别介绍了国内外的研究情况. 从中可以看出，求解仍是学者们研究Riccati方程工作的重点， 对它的应用主要是寻求其他微分方程的精确解, 实际应用方面的工作较少.

二次Riccati 方程，精确解，解的性质，Riccati 方程的应用

1 Riccati 方程的历史发展

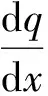
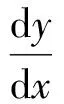
(1)

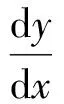
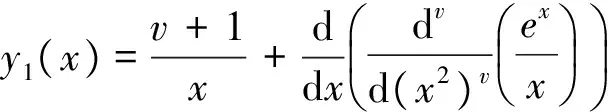
Riccati本人给出Riccati方程的求解方法，只要知道它的一个特解Y(x)，则引入z(x)=y(x)-Y(x)，可得Bernoulli方程

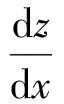
Riccati还给出，如果知道Riccati方程的两个特解y1(x)，y2(x)，则由

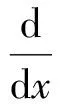
及

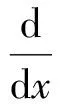
可有

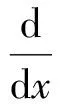
即通解可写成

其中c是常数。注意到右方只与p及y1(x)、y2(x)有关，因此，如果还知第三个解y=y3(x)，

则立即可得通解形式为[2]

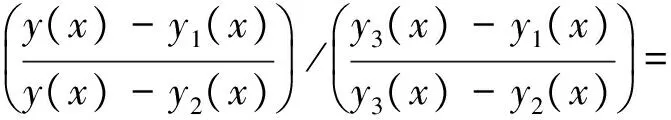
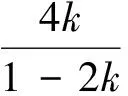
Liouville证明了Riccati方程一般没有初等解法, 即由初等积分法不能得到由初等函数表示的解. 但是很多实际问题与理论问题又迫切需要这个方程的解,比如出现在共形变换和单复变函数理论中的三阶施瓦兹微分方程, 描述浅水波运动的KdV方程, 科学与工程中的鲁棒稳定性、最优控制、扩散问题、随机过程等. 可惜, 近三百年来都未能从根本上解决这个方程, 使它成为世界著名难题. 我国学者林文业在2010年出版的《现代数学与量子力学》中用独创的多重积分迭代级数法彻底解决了这个难题.

对Riccati方程与二阶线性微分方程之间的关系和它的解的研究一直是学者们关心的问题.E. 卡姆克指出Riccati方程的一些可积情况、解的个数、任意四个解的交比为任意常数等性质.一般Riccati方程的可积和已知一个特解的求法是M Kourensky(1929年), R.Lagrange(1938年), Chiellini(1939年), L. tchacaloff(1925年)等得到的结果. Riccati微分方程和各种重要类型的二阶线性方程之间的密切关系, 整理的是M Kourensky(1926年)、D Mitrinovitch(1938年)、R Guigue(1938年)、E D Rainville(1936年)得到的结果。书中还列出了其他一些特殊形式的Riccati方程及其解[6]. 这些成果使人产生了它是艺术品之感，让人眼花缭乱，但是实质性的发展已经很少[5].

国内外对Riccati方程的推广研究各有侧重, 比如矩阵微分方程[7]、代数微分方程[8]、直至n阶的高阶微分方程[9]、分数阶微分方程[10,11]、随机微分方程[12,13,14]、离散微分方程[15]、 模糊微分方程[16]、差分微分方程[17], 等等. 由于篇幅所限, 本文主要综述2014年以来二次Riccati 微分方程的研究情况.

2 Riccati方程的研究现状

本文按文献来源分两方面介绍二次Riccati 微分方程(为方便起见下文称其为方程(1))的研究进展.

2.1 国内期刊作者对二次Riccati 方程的研究情况

国内期刊作者对Riccati微分方程的研究有方程(1)的性质、精确解、解的性质、定性理论、相关应用等, 下面分别介绍它们的研究现状.

对方程(1)研究的第二个重要方面是寻求精确解.2014年, 李松桦等通过函数替换简化了方程(1), 分析得到了一类特殊Riccati 方程的通解公式[25]. 2015年, 魏帅帅等通过齐次平衡原理和G′/G展开法对方程(1)进行求解, 得到了满足一定条件的G′/G解[26]. 何雨蔚依据几种手段求得方程(1)特殊形式的若干解[27]. 张玮玮也研究了一类特殊的方程(1), 并给出它的通解[28].唐晓等利用积分因子法考察方程(1), 给出它有积分因子的充分必要条件[29]. 2016年, 王明建等研究复常数系数的方程(1), 给出了它存在通解和常数特解的充分必要条件[30]. 套格图桑等通过研究孤子解的构造特点, 提出了复合型双孤子解的构造方法, 获得常系数方程(1)的若干解、Backlund变换和非线性解的叠加公式[31].

有的学者研究了方程(1)解的性质. 2016年, 段峰求解方程(1)的三种特殊形式, 给出了这些解之间的三个关系式[32]. 2017年, 凌云等研究了一类不能用初等积分法求解的特殊方程(1)解的存在唯一性、解最大存在区间的有界性、积分曲线的单调性和凹凸性, 也求出了它的通解[33].

利用初等积分法求解常微分方程不奏效时, 定性理论应运而生, 至今也不失为一种好方法. 2016年, 史正平考虑了二次项为1的方程(1),以临界点为突破口通过Hill方程的特征值把Riccati 方程转化为参数方程, 解答了方程(1)周期解的分支问题[34].

根据辅助方程的解寻求其他方程的解是求解时常用的方法, 常称为辅助方程(函数)法. 此方法以Tanh函数展开法为代表, 辅助方程就是方程(1)或它的变形. 这是方程(1) 在数学物理中的一个重要应用. 1990年兰慧彬、汪克林、楼森岳提出该方法, 后被Malfliet、Parkes和Duffy、范恩贵等学者推广使用. 它在求数学物理方程的精确解方面发挥了重要作用, 丰富了微分方程的研究方法. 目前微分方程领域仍有学者在应用方程(1)或其变形求解微分方程. 2012年，李晓琴利用方程(1)两类特殊形式的求解公式给出了两类二阶非线性微分方程的通解[35].2014年, 伊丽娜等利用方程(1)解的非线性叠加公式获得了带强迫项变系数耦合KdV方程的无穷序列复合型类孤子解[36].2016年, 李迎娣利用方程(1)简化形式的通积分给出了特定二阶变系数常微分方程的通积分[37].

2.2 国际期刊作者对二次Riccati 方程的研究情况

从现有文献看, 国际上对方程(1)的研究范围更加广泛：求方程(1)简化形式的精确解、数值解、近似解、具有某些解的条件、研究解的性质、研究解的物理意义、利用方程(1)(或其变形)的解求解其他方程、方程(1)的推广、方程(1)在量子力学中的应用.

2014年, 为求方程(1)的精确解, Lazhar Bougoffa提出了解决满足特定条件方程(1)的直接方法：如果方程(1)的系数函数满足一定关系, 使原方程成为变量分离方程, 就可以得到原方程的闭形式解[38]. 2015年, 楼森岳借助Riccati方程提出了求解非线性系统的相容Riccati展开法(CRE).文中将具有CRE的系统定义为可解CRE系统. 文中的方法对于各种可积系统, 包括KdV, KP, AKNS(还有非线性Schrondinger), sine-Gordon, Sawada-Kotera, Kaup-Kupershmidt, 修正非对称性 Nizhnik-Novikov-Veselov, Broer-Kaup, 弥散水波方程和Burgers系统是普遍适用的[39].Ling Xu等重新研究了基于Riccati方程的映射法, 发现有些局域结构的分离变量解没有物理意义, 有些分离变量解是互相等价的[40].Zaid Odibat2017年也提出了一种以Riccati方程命名的方法以寻求非线性演化方程的行波解. 用此方法可获得孤子解、扭结解和周期解, 解的形式有双曲线函数, 三角函数和有理函数[41]. Zaid Odibat在2016年还研究过分数阶的二次Riccati方程, 提出一种基于最优同伦渐近法(OHAM).OHAM的优点是可以通过只有一个辅助参数的同伦分析法(HAM)调整辅助参数、收敛速度和基数解的区域[42].Z.Navickas等提出了求解的逆平衡方法和直接平衡法, 可构造n次多项式系数广义Riccati方程的扭结孤立波解. 根据方程的参数和初始条件, 推出了方程存在扭结孤立波解的充分必要条件[43].

为求方程(1)的数值解,2016年,Gemechis File等为求二次Riccati方程的数值解引进了四阶Runge Kutta(RK4)法[45].2017年, Fateme Ghomanjani等介绍了一种求解带初值的二次Riccati方程和Riccati差分微分方程的方法.在这种技术中用Bezier曲线方法被作为算法去寻找这两个非线性方程的近似解[46]. Mehmet G. S. 2017年提出迭代再生核Hilbert空间法(IRKHSM)来获得常系数和变系数Riccati方程的数值解.在内积空间W2中通过再生核空间表示了Riccati方程的精确解,进一步由截断展开得到了Riccati方程的数值解,并且数值解的误差也单调减小,作者所提出的方法操作简便而富有成效[47].

借助方程(1)及其推广、变形寻求其他方程的精确解是Riccati方程应用的一个重要方面.2016年, Boudoue Hubert Malwe等研究了非线性的传输线方程, 通过广义Riccati方程映射法得到了方程的行波解、三角函数解、双曲函数解和有理函数解等[48].Hyunsoo Kim等首先建立了描述捕食者的时空扩散动力学微分方程, 该方程由两个耦合的非线性微分组成, 其中的猎物兽均增长率据Allee效应而定.使用广义Riccati方程法使作者得到了两个具有不同波速的精确解[49]. A H. Arnous等也在2016年通过方程(1)简化形式的Backlund变换等方法求解了Drinfel’d-Sokolov-Wilson方程, 得到了它的孤子解、奇异周期解等[50]. 2017年, Yakada Salathiel等通过广义Riccat方程映射法研究了描述离散电子晶格的Salerno方程, 在上、下禁制带隙得到了它的超越函数解和三角函数解, 选择适当的参数时得到了扭结孤子解、反扭结孤解子、呼吸子解、暗孤子解和亮孤子解等[51].同年, Sirendaoreji 首先构造了常系数Riccati方程的Bäcklund变换获得了解叠加公式, 从Bäcklund变换得到了Riccati方程的两分数类解, 证明新旧解之间的等价关系, 提出了所谓的统一Riccati方程展开法, 由例子证实此方法可以得到非线性发展方程的无穷多精确行波解[52].Xiao-Jun Yang等提出了局部分数阶Riccati微分方程方法, 并用该方法求解了分数阶二维Burgers型方程(2DBE)得到了该方程的不可微精确行波解[53].

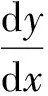
Riccati 微分方程在量子动力学中的应用, 很早就有学者研究. J. de Lucas等研究了有限维赋范分裂代数的Riccati方程, 证明有限维赋范分裂代数上的Riccati方程是欧几里德空间上共形Riccati方程的特殊情况, 也可以认为是与旋转群同构的矢量场李代数V的一条曲线. 将一种新Riccati方程, 即八元Riccati方程, 扩展到八次投影线. 使用四元数Riccati方程研究1+1维下的四元数Schrodinger方程[55]. 2015年, Han Cruz等借助非线性复Riccati方程证明量子不确定性演化的敏感性是由初始条件的选择造成的, 使得量子动力学得以重新描述. 系统的敏感性是通过它高斯波包形式的精确解来证明的[56]. 2016年, Han Cruz等把以前处理敏感性的方法应用于描述耗散量子系统. 通过简单的例子说明环境影响的效果：环境对量子不确定性的影响、相关函数、量子能贡献和隧道效应电流等[57]. 关于超对称量子力学(SUSY QM),Witten 认为研究量子力学因子分解法的两个超对称势是耦合Riccati方程的解. 由此, SUSY QM 中超对称的等谱势问题可以转化为复合Riccati方程解的复合问题. 2016年, Haret C. Rosu等研究了缺少线性项的耦合Riccati方程组. 薛定谔方程对应的势可以变换为Riccati方程. 单参数族等谱势的研究中, 基态的积分因子对应着Riccati方程的解. 利用一般Riccati方程的解, 通过定义Riccati方程解的复合公式得到了单参数等谱势的广义Mielnik结构. 用此方法研究了控制两口井的势参数时获得了一个有趣的结果, 对取某些值的参数来说小井深度定位的概率高于大井的概率[58].

2.3 对二次Riccati方程研究的预测

国内外学者用各种各样的方法求解是对二次Riccati方程研究的主流，其中最多的是求它的精确解，但是实质性的进展较少，其次是求它的数值解，求近似解的相当少. 求数值解最常用方法是经典的龙格库塔法，其他学者以后再求二次Riccati方程的数值解时，可以针对它的特点用一些其他方法，精度可能也不会太差. 求二次Riccati方程的近似解也可以作为今后一个研究方向. 在微分方程发展早期，数学家庞加莱和李雅普诺夫分别提出了定性理论和稳定性理论. 对二次Riccati方程的研究，学者们也可以尝试这两种理论. 有些物理学和工程学学者比较关心长时现象的研究，可以尝试求解. 因为Riccati方程与Schroding方程、Bessel方程等有联系，可以研究Riccati方程的近似解或解释解的物理意义.

3 结束语

综上所述, 对方程(1)的求解仍然是学术界感兴趣的问题, 国际期刊作者比国内期刊作者研究的范围更广更深，把它作为辅助函数/方程求解其他微分方程是近代的主旋律. 在应用方面, 国际期刊作者对Riccati方程研究较少, 国内学者对Riccati方程应用研究更少. 无论是国内学者还是国际学者都需要加强. 我国学者林文业关于Riccati方程所做的工作, 在国际学者的文献中没有引用, 说明并未引起足够的重视.在二十世纪以前方程(1)的可积性和精确解已经给出若干结果, 文中所引文献少部分作品创新点较少.

2014年之前很多优秀文献没有介绍，2014年以来的某些文献也不了解, 使我们对进展介绍不全面.限于篇幅, 本文对矩阵方程、代数方程等Riccati方程的推广、对Riccati方程应用中的最优控制、稳定性等讨论较少.鉴于Riccati方程的重要性, 学者们一定会对它继续研究、继续关注.

[1] Morris Kline. Mathematical Thought from Ancient to Modern Times[M]. 朱学贤,申又枨, 叶其孝;等,译.2二册.上海:上海科学技术出版社,2002.

[2] 秦元勋.常微分方程概貌[M]. 上海:科学技术文献出版社,1989.

[3] 伍卓群,李勇.常微分方程[M].北京:高等教育出版社,2015.

[4] 丁同仁,李承志.常微分方程教程[M].北京:高等教育出版社, 2014.

[5] 秦元勋.常微分方程定义的积分曲面[M]. 西安:西北大学出版社,1985.

[6] E卡姆克.常微分方程手册[M]. 张鸿林,译. 北京:科学出版社, 1977.

[7] Tayyebe Haqiri, Federico Poloni. Methods for verified stabilizing solutions to continuous-time algebraic Riccati equations[J]. Journal of Computational and Applied Mathematics, 2017,313(15):515-535.

[8] 岳聪,任兴民,邓旺群,等.航空发动机转子突加不平衡参数分析及LQR控制技术应用[J]. 振动与冲击,2015,34(17):174-179.

[9] Robert M. Yamaleev. Representation of solutions of n-order Riccati equation via generalized trigonometric functions[J]. Journal of Mathematical Analysis and Applications, 2014, 420(1):334-347.

[10] Lu Bin. Backlund Transformation of fractional Riccati Equation and infinite sequence solutions of nonlinear fractional PDEs[J]. Abstract and Applied Analysis, 2014, ID: 572052, 6ps.

[11] M Pardaman, A Ahmadian, S Effati,et al. Solving differential equations of fractional order using an optimization technique based on training artificial neural network[J]. Applied Mathematics and Computation, 2017,293: 81-95.

[12] Stephane Gaubert, Zheng Qu. The contraction rate in thompson’s part metric of order-preserving flows on a cone application to generalized riccati equations[J].Journal of Differential Equations, 2014,256: 2 902-2 948.

[13] Li Na, Wu Zhen, Yu Zhi-yong. Indefinite stochastic linear-quadratic optimal control problems with random jumps and related stochastic Riccati equations[J]. Science China Mathematics, 2017.doi: 10.1007/s11425-015-0776-6.

[14] Tien Dung Nguyen, Hanoi. Gaussian density estmates for the solution of singular stochastic Riccati equtions[J].Applications of Mathematics, 2016, 61(5): 515-526.

[15] Eric King-wah Chu, Peter Chang-Yi Weng. Large-scale discrete-time algebraic Riccati equationsDoubling algorithm and error analysis[J].Journal of Computational and Applied Mathematics, 2015(277): 115-126.

[16] Sh Sadigh Behzadi, Behnam Vahadani, T. Allahviranloo.et al. Application of fuzzy Picard method for solving fuzzy quadratic Riccati and fuzzy painleve I equations[J].Applied Mathematical Madelling 2016(40): 8 125-8 137.

[17] Huan Zhang, Peter M Dower. Max-plux fundamental solution semigroupps for a class of difference Riccati equations[J]. Proceedings of the 19th International Symposium on Mathematical Theory of Networks and Systems-MTNS, Budapest, Hungary,2010.

[18] 王明建,王五生,石东洋.一类一阶微分方程与Riccati方程的等价关系[J].河南科学, 2014,32(4): 479-481.

[19] 段峰,赵临龙,张兰.Riccati 方程的几个性质及其应用[J].首都师范大学学报:自然科学版,2014,35(6):9-13.

[20] 段峰.Riccati方程的初等变换及其应用[J].内江科技, 2015, 36(8): 63-64.

[21] 段峰.Riccati 方程的几个新的性质及其应用[J].中央民族大学学报:自然科学版, 2015,24(2): 21-26.

[22] 段峰,张兰,孙擎.Riccati方程的几个新的可积性判据[J].湖南理工学院学报:自然科学版, 2014,27(1): 24-27.

[23] 段峰,赵临龙,张兰.关于Riccati 方程可积性的研究[J].湖南学院学报,2014,35(2): 14-19.

[24] 段峰,张兰,杨芬.Riccati方程的几种可积类型及其通积分公式[J].中央民族大学学报:自然科学版,2014,23(3): 10-13.

[25] 李松桦,张泽川.一类Riccati微分方程的通解公式[J].湖南理工学院学报:自然科学版,2014,27(1):28-30.

[26] 魏帅帅,李凯辉,刘汉泽.G′/G展开法在Riccati 方程中的应用[J].河南科技大学学报:自然科学版, 2015,36(5):92-97.

[27] 何雨蔚.Riccati微分方程解的探讨[J].攀枝花学院学报, 2015,32(2):66-69.

[28] 张玮玮.一类特殊类型的Riccati 方程的求解[J].安庆师范学院学报:自然科学版,2015,21(2):110-111.

[29] 唐晓,刘翠萍,周恺.积分因子法在两类微分方程求解中的应用[J].高师理科学刊,2015,35(8):26-28.

[30] 王明建,胡博,王桂花.复系数Riccati 微分方程解的存在条件及应用[J]. 西安文理学院学报:自然科学版,2016,19(3): 34-36.

[31] 套格图桑,伊丽娜.一类非线性发展方程的复合型双孤子新解[J]. 物理学报,2015,64(2):12-23.

[32] 段峰.几类可积的Riccati 方程解的性质[J].中央民族大学学报:自然科学版,2016,25(1):27-31.

[33] 凌云,李满枝.一类Riccati 方程解的性质[J].海南热带海洋学院学报,2017,24(2):43-46.

[34] 史正平.Riccati 方程周期解的分支[J]. 数学的实践与认识, 2016,46(1):284-288.

[35] 李晓琴.二阶非线性微分方程Riccati 方程的解法及应用[J].聊城大学学报,2012,25(2):19-21.

[36] 伊丽娜,套格图桑.带强迫项变系数组合KdV方程的无穷序列复合型类孤子解[J]. 物理学报,2014,63(3): 1-8.

[37] 李迎娣.二阶变系数线性齐次微分方程的一些解法[J].西北民族大学学报:自然科学版, 2015,936(3): 1-2.

[38] Lazhar Bougoffa. New conditions for obtaining the exact solutions of the general Riccati equation[J]. The Scientific World Journal, 2014(2014):1-8.

[39] Lou S Y. Consistent Riccati expansion for integrable systems[J]. Studies in Applied Mathematics, 2015,134 (3):372-402.

[40] Xu Ling,Cheng Xuan,Dai Chao-qing. Discussions on equivalent solutions and localized structures via the mapping method based on Riccati equation[J]. The European Physical Journal Plus, 2015,130(12):242-249.

[41] Zaid Odibat.A Riccati equation approach and travelling wave solutions for nonlinear evolution equations[J]. Int J Appl Comput Math,2017,3: 1-13.

[42] Zaid Odibat. An analytic solution for fractional order Riccati equations by using optimal homotopy asymptotic Method[J]. Applied Mathematical Sciences, 2016,10(23):1 131-1 150.

[43] Navickas Z, Ragulskis M, Marcinkevicius R, et al. Kink solitary solutions to generalized Riccati equations with polynomial coefficients[J]. Journal of Mathematical Analysis and Applications, 2017,448: 156-170.

[44] Yasar Pala, Mutlu Ozgur Ertas. A new analytical method for solving general Riccati equation[J]. Universal Journal of Applied Mathematics,2017,5(2): 11-16.

[45] Gemechis File, Tesfaye Aga. Numerical solution of quadratic Riccate differential equations[J]. Egyptian journal of basic and applied sciences, 2016 (3):392-397.

[46] Fateme Ghomanjani, Esmaile Khorram. Approximate solution for quadratic Riccati differential equation[J]. Journal of Taibah University for Science, 2017, (11): 246-250.

[47] Mehmet G. S. Iterative reproducing kernel Hibert spaces method for Riccati differential equations[J]. Journal of computational and Applied Mathematics, 2017 (309): 163-174.

[48] Boudoue Hubert Malwe, Gambo Betchewe, Serge Y Doka, et al. Travelling wave solutions and soliton solutions for thenonlinear transmission line using the generalized Riccatiequation mapping method[J]. Nonliner Dyn, 2016, 84:171-177.

[49] Hyunsoo Kim, Jin Hyuk Choi. Exact solutions of a diffusive predator-prey systemby the generalized Riccati equation[J]. Bull Malays Math Sci Soc, 2016,(39):1 125-1 143.

[50] Arnous A H, Mirzazadeh M, Eslami M. Exact solutions of the Drinfel’d-Sokolov-Wilson equation using Backlund transformation of Riccati equation and trial function approach[J]. Pramana-journal of physics, 2016,86(6):1 153-1 160.

[51] Yakada Salathiel, Yaouba Amadou, Gambo Betchewe, et al. Soliton solutions and traveling wave solutions for a discrete electrical lattice with nonlinear dispersion through the generalized Riccati equation mapping method[J]. Nonlinear Dyn, 2017,(87): 2435-2443.

[52] Sirendaoreji. Unified Riccati equation expansion method and its application to two new classes of Benjamin-Bona-Mahony equations[J]. Nonlinear Dyn, 2017,89:333-344.

[53] Yang Xiao-Jun, Gao Feng, Srivastava H M. Exact travelling wave solutions for the local fractional two-dimensional Burgers-type equations[J]. Computers and Mathematics with Applications, 2017(73): 203-201.

[54] Armengol Gasull, Joan Torregrosa, Xiang Zhang. The number of polynomial solutions of polynomial Riccati equations[J].J Differential Equations, 2016,(261): 5 071-5 093.

[55] Lucas J de, Tobolski M, Vilarino S.Geometry of Riccati equations over normed division algebras[J]. Journal of Mathematical Analysis and Applications, 2016, (440): 394-414.

[56] Han Cruz, Dieter Schuch, Octavio Castanos, et al. Time-evolution of quantum systems via a complex nonlinear Riccati equation. I. Conservative systems with time-independent Hamiltonian[J]. Annls of Physics, 2015, (360): 44-60.

[57] Han Cruz, Dieter Schuch, Octavio Castanos, et al. Time-evolution of quantum systems via complex nonlinear Riccati equation. II. Dissipative systems[J]. Annls of Physics, 2016, (373): 609-630.

[58] Haret C Rosu, Stefan C Mancas, Pisin Chen. One-parameter families of supersymmetric isospectral potentials from Riccati solutions in function composition form[J]. Annals of Physics, 2014, (343): 87-102.

ReviewofQuadraticRiccatiEquation

LIU Yu-tang XIN Xiang-peng

(School of Mathematical Sciences, Liaocheng University, Liaocheng 252059, China)

A brief basic situation of the Riccati equation is introduced including some results and the significance of its research. The research progress of the Riccait equation is analyzed from domestic and international literatures from 2014 to the present. The research situation are expounded at home and abroad in the view of the nature of the equation itself, integrable properties, exact solutions, numerical solutions, the qualitative theory and the applications. It can be seen that the solutions is still the focus of the study of the quadratic Riccati equation, and its application is mainly to find exact solutions to the other differential equations, the practical application of the quadratic Riccati equation is rarely done.

the quadratic Riccati differential equation, exact solution, properties of solutions, applications of the Riccati equation

2017-04-20

国家青年科学基金项目(11505090)；山东省自然科学基金中青年科学家奖励基金( BS2015SF009)资助

刘玉堂,E-mail：liuyutang2008@sina.com.

O175.2

A

1672-6634(2017)03-0021-05