模糊子集的(λ,μ)-限制生成的模糊代数结构①

吕艳瑞 李令强

(聊城大学 数学科学学院，山东 聊城 252059)

模糊子集的(λ,μ)-限制生成的模糊代数结构①

吕艳瑞 李令强

(聊城大学 数学科学学院，山东 聊城 252059)

对环的任意模糊子集A和一对实数0≤λ<μ≤1,定义了A的(λ,μ)-限制,构造了其生成的模糊子(半)环与模糊理想.

模糊子环, 模糊理想, 生成模糊子环, 生成模糊理想

0 引言

1965年,为了处理对象信息的不确定性, Zadeh[1]采用隶属度方法来描述点对集的隶属关系,引入了模糊集的概念. 1971年, Rosenfeld[2]把这种方法引入代数, 提出了模糊群的概念. 随后,人们也把环和理想等代数结构推广到了模糊领域中. 2008年,姚炳学教授在其专著[3]中详细地介绍了群与环的模糊理论. 特别的,对任意一对实数0≤λ<μ≤1,姚炳学教授引入了(λ,μ)-模糊群、(λ,μ)-模糊环和(λ,μ)-模糊理想等模糊代数结构. Rosenfeld的模糊群可以看做(0,1)-模糊群.所以,(λ,μ)-模糊代数结构是一种更广泛的模糊结构.近年来,人们对(λ,μ)-模糊代数的研究逐渐展开,取得了一些有意义的成果[4-10]. 对环的任意模糊集A,本文将定义A的(λ,μ)-限制,并构造其生成的模糊子(半)环与模糊理想.

1 预备知识

本文中R=(R,+,·)表示一个环,N为自然数,λ,μ为常数且0≤λ<μ≤1.若A,B为环R的模糊子集,定义模糊子集A+B,A-B,A·B,-A如下:∀x∈R,

(A+B)(x)=∨{A(y)∧B(z)|x=y+z},(A-B)(x)=∨{A(y)∧B(z)|x=y-z},
(A·B)(x)=∨{A(y)∧B(z)|x=y·z},(-A)(x)=A(-x).

另外,称A包含于B,记作A⊆B若:∀x∈R,A(x)≤B(x).

定义1[3]设A为环R的模糊子集.

若A满足:∀x,y∈R,A(x+y)≥A(x)∧A(y),A(-x)≥A(x),则称A为环R的模糊子加群;

若A满足:∀x,y∈R,A(x+y)≥A(x)∧A(y),A(xy)≥A(x)∧A(y),则称A为环R的模糊子半环;

若A满足:∀x,y∈R,A(x+y)≥A(x)∧A(y),A(xy)≥A(x)∧A(y),A(-x)≥A(x),则称A为环R的模糊子环.

定义2[3]设A为环R的模糊子集. 若任取x,y∈R

A(x+y)∨λ≥(A(x)∧A(y))∧μ,A(xy)∨λ≥(A(x)∧A(y))∧μ,

则称A为环R的一个(λ,μ)-模糊子半环.

定义3[3]设A为环R的模糊子半环. 若任取x,y∈R,A(-x)∨λ≥A(x)∧μ,则称A为环R的一个(λ,μ)-模糊子环. 显然,A为(λ,μ)-模糊子环的充要条件为:∀x,y∈R,

A(x-y)∨λ≥(A(x)∧A(y))∧μ,A(xy)∨λ≥(A(x)∧A(y))∧μ.

定义4[3]设A为环R的模糊子集. 若任取x,y∈R,

A(x-y)∨λ≥(A(x)∧A(y))∧μ,A(xy)∨λ≥(A(x)∨A(y))∧μ,

则称A为环R的一个(λ,μ)-模糊理想.

2 模糊子集的(λ,μ)-限制生成的模糊子(半)环与模糊理想

定理1 设A为环R的模糊子(半)环、模糊理想,则A为R的(λ,μ)-模糊子(半)环、模糊理想.

证明文献[3]利用模糊集的截集证明了该结论,我们直接用定义来证明. 以模糊子半环为例, 其它情形类似. 任取x,y∈R,由A为R的模糊子半环得

A(x+y)∨λ≥(A(x)∧A(y))∨λ=(A(x)∨λ)∧(A(y)∨λ)
≥(A(x)∧μ)∧(A(y)∧μ)=A(x)∧A(y)∧μ.
A(xy)∨λ≥(A(x)∧A(y))∨λ=(A(x)∨λ)∧(A(y)∨λ)
≥(A(x)∧μ)∧(A(y)∧μ)=A(x)∧A(y)∧μ.

综上,A为R的(λ,μ)-模糊子半环.

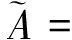
定理2 设A为环R的模糊子集, 则如下定义的模糊子集(A)

是环R的一个模糊子半环, 当然也是(λ,μ)-模糊子半环.

证明任取x,y∈R,有

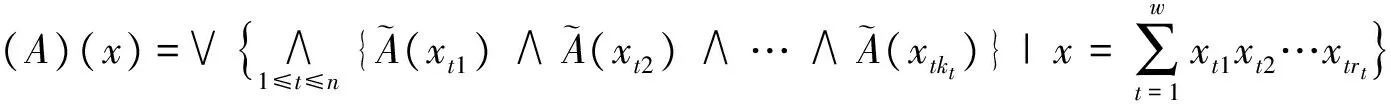
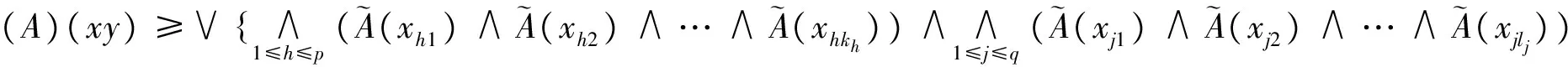
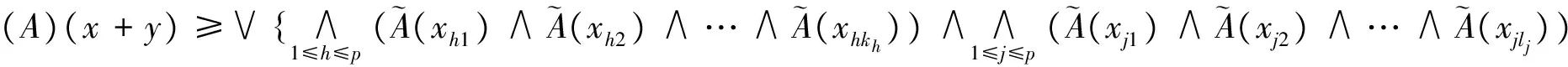
因此,(A)是R的模糊子半环.

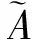
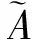
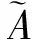
定义6 设A为环R的模糊子集, 称(A)为A的(λ,μ)-限制生成的模糊子半环.

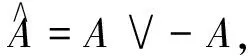
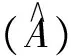
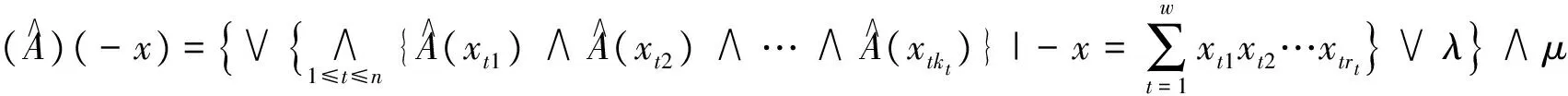
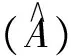
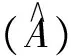
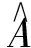
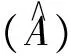
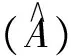
定理6 设A为环R的模糊子集, 则如下定义的模糊集[A]

是环R的一个模糊理想, 当然也是(λ,μ)-模糊理想.

证明任取x,y∈R,有

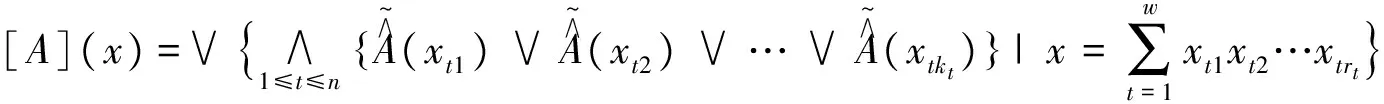
同理可得,[A](xy)≥[A](y),故[A](xy)≥[A](x)∨[A](y).综上,[A]是R的模糊理想.

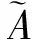
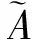
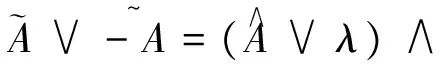
所以

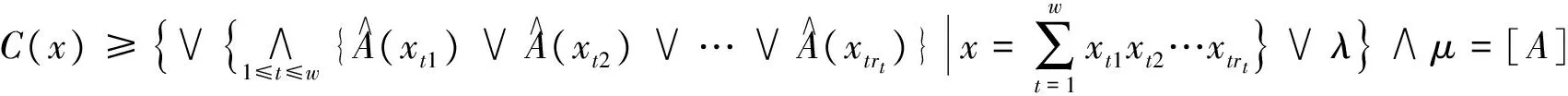
定义8 设A是环R的模糊子集, 称[A]为A的(λ,μ)-限制生成的模糊理想.

3 结语

本文对环的任意模糊子集A,构造了包含其(λ,μ)-限制的最小模糊子(半)环和模糊理想.值得注意的是,任意一族(λ,μ)-模糊子(半)环和(λ,μ)-模糊理想的交仍然是(λ,μ)-模糊子(半)环和(λ,μ)-模糊理想,且最大的模糊子集,即取常值1的模糊子集是(λ,μ)-模糊子(半)环和(λ,μ)-模糊理想. 所以, 对环的任意模糊子集A, 存在包含A的最小的(λ,μ)-模糊子(半)环和(λ,μ)-模糊理想. 我们将在稍后的工作中对此展开讨论.

[1] Zadeh L A. Fuzzy sets[J]. Inform and Control， 1965, 8(1): 338-353.

[2] Rosenfeld A. Fuzzy groups[J]. Math Anal Appl， 1971, 35: 512-517.

[3] 姚炳学.群与环上的模糊理论[M].北京:科学出版社,2008.

[4] Yao B X .(λ,μ)- fuzzy normal subgroups and(λ,μ)-fuzzy quotient subgroups[J]. The Journal of Fuzzy Mathematics, 2005, 13: 695-705.

[5] Yao B X .(λ,μ)-fuzzy subrings and(λ,μ)-fuzzy ideals[J]. The Journal of Fuzzy Mathematics, 2007, 15:981-987.

[6] 刘俊兰,姚炳学.模糊同态下的(λ,μ)-模糊子环[J]. 聊城大学学报:自然科学版,2010,23(1): 14-16.

[7] 李玉瑛,王绪柱.(λ,μ)-模糊子群的运算[J].模糊系统与数学,2014,28(2):46-51.

[8] 郝翠霞,姚炳学.(λ,μ)-商模糊子群及其同构定理[J].模糊系统与数学,2015,29(1): 35-42.

[9] 周峰,姚炳学.(λ,μ)-模糊软环与(λ,μ)-模糊软理想[J].河南科技大学学报:自然科学版,2015, 36(5):97-99.

[10] 王爽.环上的(λ,μ)-模糊n伪理想与(λ,μ)-模糊拟理想[J].聊城大学学报:自然科学版, 2016,29(3):5-7.

TheFuzzyAlgebraicStructureGeneratedby(λ,μ)-RestrictionofFuzzySubsets

LV Yan-rui LI Ling-qiang

(School of Mathematical Sciences, Liaocheng University, Liaocheng 252059, China)

For arbitrary fuzzy subsetofAof a ring and a pair of real numbers (λ,μ) with 0≤λ<μ≤1, the notion of restriction ofAis defined; and then the fuzzy subrings (subsemi-rings) and fuzzy ideals generated by the restriction are constructed, respectively.

fuzzy subring，fuzzy iedal，(λ,μ)-fuzzy subring，(λ,μ)-fuzzy ideal

2017-05-08

国家自然科学基金项目(11501278)资助

李令强，E-mail：lilingqiang@126.com.

O153

A

1672-6634(2017)03-0012-05