旋翼桨尖涡生成及演化机理的高精度数值研究

叶舟,徐国华*,史勇杰

南京航空航天大学 直升机旋翼动力学国家级重点实验室,南京 210016

旋翼桨尖涡生成及演化机理的高精度数值研究

叶舟,徐国华*,史勇杰

南京航空航天大学 直升机旋翼动力学国家级重点实验室,南京 210016

为了细致捕捉直升机旋翼桨尖涡的生成和演化过程,建立了一个基于高精度网格和高阶通量计算格式的旋翼桨尖涡计算流体力学(CFD)求解方法。在该方法中,流场求解选取旋转坐标系下的Navier-Stokes方程为控制方程;空间离散采用迎风Roe格式,并采用低耗散的5阶WENO(Weighted Essentially Non-Osciltatory)格式进行对流通量的计算;时间推进则采用双时间法,在伪时间步上使用隐式LU-SGS(Lower-Upper Symmetric Gauss-Seidel)推进格式;应用嵌套网格方法实现桨叶网格和背景网格的数据交换。应用所建立的方法对悬停状态的旋翼桨尖涡流场进行了高精度模拟,在桨叶网格上精细地捕捉到了桨尖涡的具体生成过程,在背景网格上捕捉到了更多圈数的桨尖涡尾迹,并对桨尖涡的演化机理进行了深入研究。结果表明:建立的高精度数值方法能够有效地对旋翼桨尖涡的生成和演化过程进行细致模拟;悬停状态下旋翼桨尖气流在上下表面压力梯度的作用下经历了边界层增厚、逐渐卷起形成涡核以及最终脱离桨叶形成桨尖涡的过程。

桨尖涡;WENO格式;嵌套网格;计算流体力学;旋翼;直升机

直升机以其独特的垂直起降和空中悬停等特点在军事和民用领域中发挥了重要的作用,而正是旋翼这个特殊部件赋予了直升机如此特异的性能。然而,也正是因为旋翼的存在,直升机也承受着各种气动干扰问题,进而给直升机的噪声和振动等带来很大影响。在工作状态下,旋翼的旋转会产生较强的涡流场,从桨叶尖端脱落的桨尖涡会与直升机的其他部件甚至是旋翼其他桨叶发生干扰,因此,开展旋翼桨尖涡的生成机理和演化过程研究具有重要的理论和实际意义。

先前,旋翼桨尖涡的研究大多是通过试验手段来开展的,而试验技术水平则随着现代测量设备的进步而提升。2000年,Heineck等[1]通过PIV(Particle Image Velocimetry)对悬停状态下旋翼0°～270°涡龄角的桨尖涡尾迹进行了测量,观测到了旋翼桨尖涡的内部结构。同年,Martin等[2]则采用PIV和LDV(Laser Doppler Velocimetry)2种设备对旋翼桨尖涡进行了试验,并详细对比了这2种方法的差异,为之后的试验测量提供了较好的依据。2001年,Wong和Komerath[3]使用LDV对低速前飞状态下的旋翼桨尖涡进行了测量,获得了其488°涡龄角内的桨尖涡尾迹分布。在此之后还有一些研究者对旋翼桨尖涡进行了试验[4-6],虽然能够直观地显示出旋翼桨叶脱落的桨尖涡,但由于试验本身的局限性,却不能对桨尖涡的具体生成过程进行捕捉并可视化,且不能观测更大涡龄角范围的桨尖涡尾迹。

近年来,随着计算流体力学(CFD)技术的快速发展,使得采用数值模拟方法研究桨尖涡的生成及演化机理成为可能。数值方法能够弥补试验手段的不足,且成本更低,因此逐渐成为旋翼桨尖涡流场研究的热点。例如,2007年,美国马里兰大学的Duraisamy等[7]采用CFD方法对具有矩形桨尖的桨叶进行了桨尖涡的数值计算,其计算结果与试验测量数据大体吻合,表明了CFD方法在桨尖涡研究中的可靠性。最近,一些学者进一步采用高精度CFD方法[8-10]开展了旋翼桨尖涡的数值研究,但他们主要都是针对旋翼桨尖涡尾迹的演化以及与其他部件的气动干扰方面,尚未涉及桨尖涡的形成机理和演化规律研究。这是因为,旋翼桨尖涡的CFD模拟对计算网格和计算格式要求很高,具有相当的难度。因此,深入开展旋翼桨尖涡的形成机理和演化规律研究具有良好的学术价值。

鉴于此,本文拟发展一个适用于旋翼桨尖涡的生成及演化研究的高精度CFD求解器。为了对桨尖涡涡核进行精细捕捉,提出了高精度的旋翼桨叶网格生成及加密方法,并重点建立了低数值耗散的5阶WENO(Weighted Essentially Non-Oscillatory)通量求解格式,以模拟桨尖涡的演化进程。采用建立的方法对悬停状态下的旋翼桨尖涡进行了数值模拟,结果表明:在旋翼桨尖涡的远场演化过程中,存在一个收缩极限使得桨尖涡收缩到此位置便开始向外扩张。而且,旋翼桨尖涡的下降和收缩速度等特性与桨尖马赫数和总距等参数密切相关。

1 旋翼涡流场高精度数值计算方法

1.1 旋翼悬停流场求解方法

对于悬停状态的旋翼准定常流场,采用旋转坐标系下的Navier-Stokes方程[11]进行数值求解,其表达式为

式中:W、Fc、Fv和Q分别为守恒变量、无黏通量、黏性通量和源项,可分别表示为

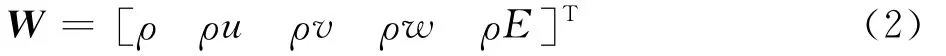
式中:u、v和w分别为流体运动速度的3个轴向分量;Ω为旋翼旋转角速度;τ为黏性应力;U 为桨叶在计算位置上与流体的相对速度,ρ为流体密度;p为流体压力;[nxnynz]T为控制面在x、y和z方向的面法矢;Θ为黏性力和热传导对流体的功;H为单位质量流体的总焓。

在空间离散方面,采用迎风Roe格式[12]针对控制面对流通量进行计算,其表达式为

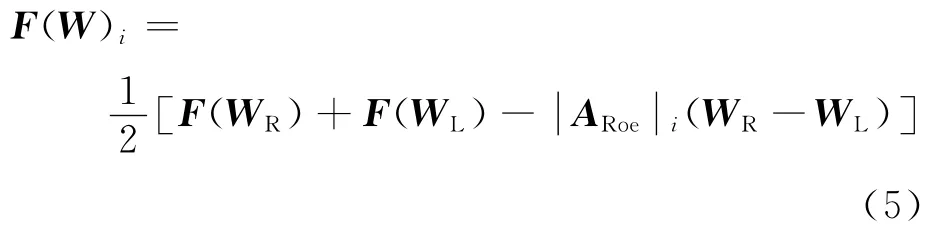
式中:F(W)i为控制面上的对流通量,i为控制面编号;F(WR)和F(WL)分别为控制面右侧和左侧的对流通量;为Roe矩阵。为了闭合式(5),采用5阶WENO格式[13]对控制面左右两侧的原始变量进行插值计算。对于5阶WENO格式而言,其涉及的模板数与3阶ENO格式是相同的,但是,WENO格式不涉及模板的选择问题,并且在光滑区精度较高。

如图1所示,网格单元I对应I-1/2和I+1/2两个控制面,在求解控制面I-1/2右侧和控制面I+1/2左侧的原始变量时,选取的模板是一致的,均为单元I-2、I-1、I、I+1和I+2。在计算网格均匀的前提下,控制面I+1/2左

图1 WENO格式模板选择Fig.1 Template selection for WENO scheme

侧和I-1/2右侧的原始变量求解公式为

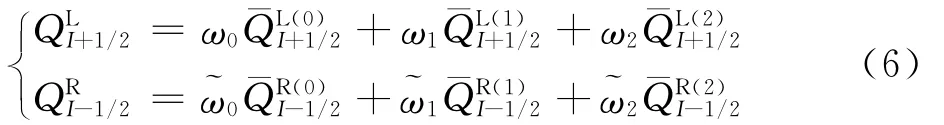
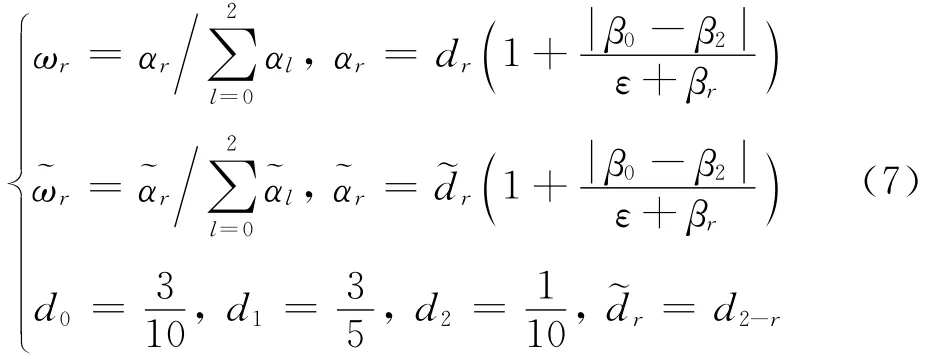
式中:β为光滑因子,控制面I-1/2和I+1/2的光滑因子求解方法一致,均可由所选模板格心的原始变量计算得到;ε为小量,取值10-6,用于避免分母为0。

在计算域边界处,可采用3阶ENO格式或者降阶的3阶WENO格式对控制面左侧和右侧原始变量进行计算,但是由于流场边界对整体流场影响巨大,模板选取对计算收敛性影响较大。因此,这里采用虚拟网格方法[15]对边界进行处理,从而保证边界面的5阶WENO插值。

如图2所示,在边界外添加两层虚拟网格,虚拟网格格心的原始变量值由内部流场值等梯度插值得到。需要指出的是,图中所示的插值边界有4种,即:桨叶网格物面边界、桨叶网格最外层网格边界(运动嵌套网格方法中桨叶网格没有远场边界)、背景网格远场边界和背景网格洞边界(运动嵌套网格方法中背景网格没有物面边界)。

图2 虚拟网格的定义Fig.2 Definition of dummy cells

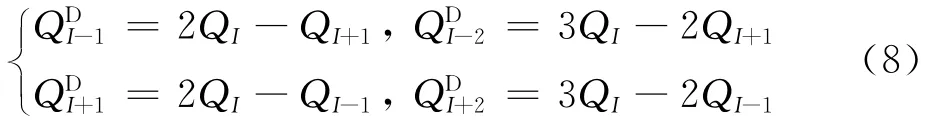
计算域边界外虚拟网格格心的原始变量的计算方法为式中:上标D表示虚拟网格(Dummy cells)。

在时间推进方面采用双时间方法,并在每个伪时间步使用高效的隐式LU-SGS(Lower-Upper Symmetric Gauss-Seidel)推进格式[16],湍流模型选取B-L(Baldwin-Lomax)模型[17]。

1.2 旋翼嵌套网格与加密

采用嵌套网格方法[18]对旋翼流场计算域进行离散,其中旋翼桨叶采用C-O型贴体网格,背景网格为C-H型,计算中生成的网格如图3所示。另外,为了有效地对旋翼桨尖涡生成和演化过程进行捕捉,需对桨叶截面的二维翼型网格进行加密。

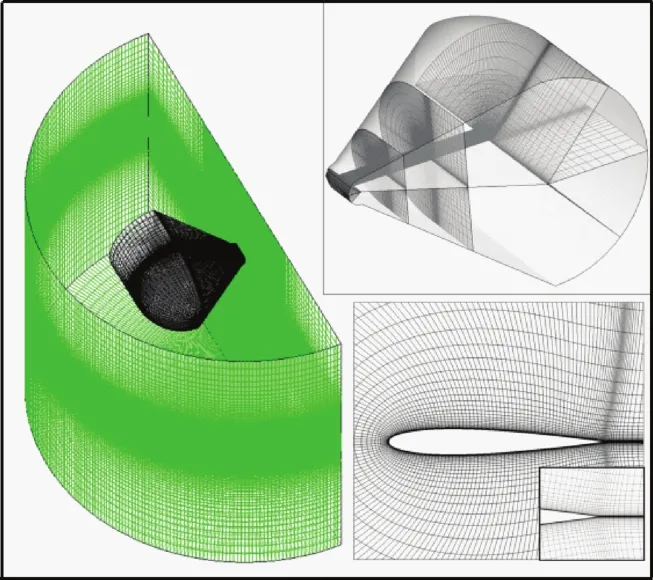
图3 悬停嵌套网格系统Fig.3 Generated overset grid system in hover

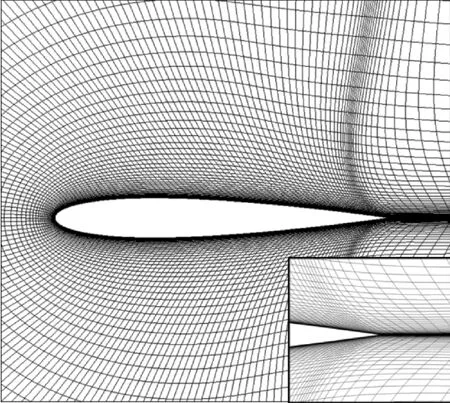
图4 正交性差的加密网格Fig.4 Refined grid with bad orthogonality

二维网格生成采用椭圆型方程[19]网格生成法,该方法能有效地对生成的网格进行正交化处理,但是如果过度增加法向的网格节点数,网格的正交性会变差,如图4所示。因此,首先采用椭圆型方程网格生成法生成正交性较好的二维翼型网格,然后在此基础上运用线性插值方法对该网格进行加密,从而使得网格密度和正交性均满足旋翼CFD计算的要求。图5是加密后的整体计算网格,由图中可见,该网格不仅实现了特定区域的网格加密还保留了原先较好的网格正交性,保证了Navier-Stokes方程求解的精度。

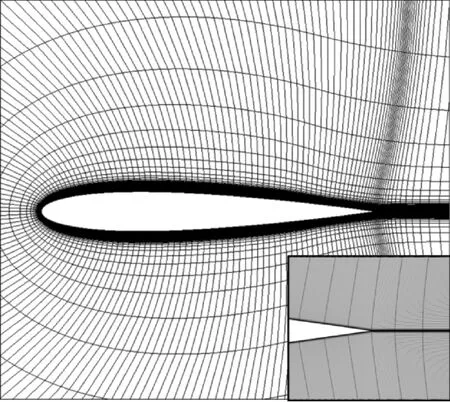
图5 正交性好的加密网格Fig.5 Refined grid with good orthogonality

2 计算方法验证

选取具有多翼型配置和复杂线性扭转分布桨叶的Helishape 7A旋翼进行验证计算,该旋翼具有4片桨叶,展弦比为15,桨叶采用了OA209和OA213两种翼型,且具有3段不同的扭转分布,总距定义在0.7R(R为桨叶半径)处。选取该旋翼桨尖马赫数为0.662,总距为7.5°的悬停试验状态[20]进行数值模拟。图6给出了Helishape 7A旋翼桨叶各截面压力系数Cp分布的计算值与试验数据的对比,图中:ψ为涡龄角;x/c为数据点的弦向位置;r/R为桨叶展向截面的径向位置。从图中可以看出,在旋翼桨叶的各段,本文计算的桨叶表面压力系数分布均能与试验数据吻合得较好。

图6 Helishape 7A旋翼桨叶各截面压力系数分布计算值与试验数据的对比Fig.6 Comparisons of calculation and test results of sectional pressure coefficients distribution of Helishape 7A blade

为了更好地对旋翼桨尖涡的生成及演化规律进行捕捉和研究,应排除特殊桨尖外形和扭转分布等造成的影响,因此,后续针对桨尖涡生成及演化的模拟和计算均选取桨叶构型相对简单的Caradonna-Tung模型旋翼。该旋翼具有2片展弦比为6的矩形无负扭转桨叶,桨叶截面翼型为NACA0012。这里对该旋翼桨尖马赫数为0.794,总距为8°的试验状态[21]进行了验证计算。图7为Caradonna-Tung旋翼桨叶截面压力系数分布计算值与试验值的对比,图中“Bkweno”表示只在背景网格上应用高阶格式计算,“Allweno”表示桨叶网格和背景网格上均采用高阶格式计算;图8为旋翼桨尖涡的等涡量图。

本文采用嵌套网格方法对旋翼流场进行模拟,所以可以分别对桨叶网格和背景网格添加高阶格式。从图7中结果可知,本文计算的桨叶截面压力系数分布能与试验值高度吻合,能较好捕捉桨叶激波,而桨叶网格添加高阶格式对桨叶截面压力系数分布的计算影响并不大;通过图8中的等涡量图的对比可见,基于 MUSCL格式的CFD方法只能捕捉到涡龄角360°左右的旋翼桨尖涡,而采用5阶 WENO格式捕捉的桨尖涡涡龄角能达到900°以上,由此可以看出5阶 WENO格式在降低旋翼桨尖涡数值耗散方面的能力。因此,若要对桨尖涡的演化进行研究,必须要在背景网格上添加高阶格式。

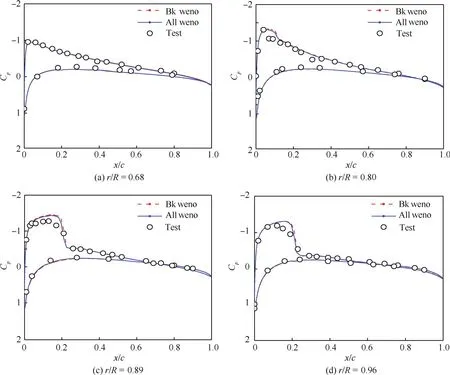
图7 Caradonna-Tung旋翼桨叶各截面压力系数分布计算值与试验数据的对比Fig.7 Comparisons of calculation and test results of sectional pressure coefficients distribution of Caradonna-Tung blade

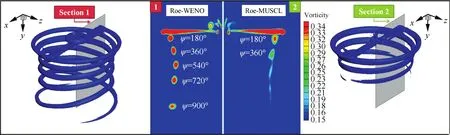
图8 Caradonna-Tung旋翼桨尖涡等涡量对比图Fig.8 Comparisons of vortex iso-vorticity faces of Caradonna-Tung blade tip

根据以上对Helishape 7A旋翼和Caradonna-Tung旋翼试验状态的计算对比可知,本文建立的数值分析方法能够有效地对旋翼流场进行模拟,可以根据需要分别对桨叶网格和背景网格应用高阶格式,能够适应不同要求的旋翼气动计算。

3 旋翼桨尖涡生成及演化计算

3.1 旋翼桨尖涡的生成

为了完整地捕捉旋翼桨尖涡的生成过程,选取Caradonna-Tung旋翼桨尖马赫数0.3、总距8°的状态进行数值模拟。在该状态下对旋翼桨尖涡的生成进行了3组计算模拟,分别为:未加密网格无高阶格式(Baseline)、加密网格无高阶格式(Refined)和未加密网格与高阶格式(Weno)。需要说明的是,为了表明加密的网格已经消除了网格量对计算精度的影响,在本节的研究开始前进行了相应的计算对比。本文加密的桨叶网格维数为225×80×150,使用该网格计算的结果与使用维数为225×150×178的桨叶网格计算的结果基本相同,这表明该网格已经满足精度要求,并且由于其网格量更小,所以具有更高的计算效率。

图9给出了“Baseline”和“Refined”2组算例计算的旋翼桨尖涡的生成过程,从图中可以大致看出旋翼桨尖涡的捕捉精度的差异,具体桨叶尖部弦向不同截面的涡量云图如图10所示。观察图9和图10可以看出,在桨叶前缘(z=0.25c)至截面z=-0.25c之间,由于旋翼桨叶上下表面压力梯度的存在,气流从桨尖下方向上方流动,然而,由于“康达效应”的作用,气流在该截面段依然吸附在桨叶端部表面。从z=-0.45c左右的位置开始,“康达效应”渐渐不能束缚上翻气流,桨叶端部的边界层开始增厚,直至截面z=-0.60c附近,端部气流开始脱离桨叶圆形端面。之后随着桨尖气流的持续向上表面流动,在桨叶后缘(z=-0.75c)处桨尖涡彻底脱离桨叶表面,最终形成成型的桨尖涡。

对比图9和图10中2组算例的计算结果可以发现,在没有进行网格加密的“Baseline”算例中,旋翼桨尖涡的生成过程也能被大致地捕捉到,但其具体流场细节的捕捉并不如“Refined”算例。例如在z=-0.60c截面处,“Baseline”算例只能捕捉到边界层的变厚现象,而“Refined”算例却能明显地捕捉到旋翼桨尖涡的脱离现象以及涡核下方旋转方向相反的二级涡,并且桨尖涡涡量的耗散也有所降低。另外,“Weno”算例计算的桨尖涡结果与“Baseline”算例相似,只是桨尖涡的数值耗散有所降低,所以未列出。由此可知,旋翼桨尖涡生成过程的模拟对桨叶网格精度要求较高,若不进行合理加密,将不能对其生成过程进行精确捕捉。

除了桨尖涡的生成过程,还对桨叶网格上旋翼桨尖涡涡核速度和涡核直径的变化进行了相关研究。以旋翼变距轴为基准,向旋翼尾迹方向分别旋转10°、20°和30°,并分别截取这3个面上旋翼桨尖涡的信息。

图9 桨尖涡的生成过程Fig.9 Formation processes of blade tip vortex

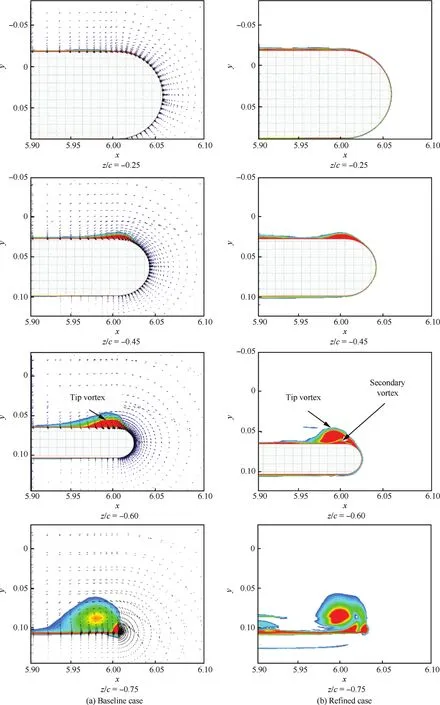
图10 不同桨叶网格桨尖涡生成过程对比Fig.10 Comparisons of blade tip vortex formation process with different blade grid

表1给出了各截面上旋翼桨尖涡的涡核速度与桨尖速度的比值Vcore/Vtip以及涡核半径与弦长的比值rcore/c。由表1可见,在10°涡龄角处“Refined”算例捕捉的桨尖涡涡核速度最大,也更接近该状态下旋翼桨尖涡的最大值[22],其次是“Weno”算例,模拟精度最低的是“Baseline”算例,具体对比如图11(a)所示。

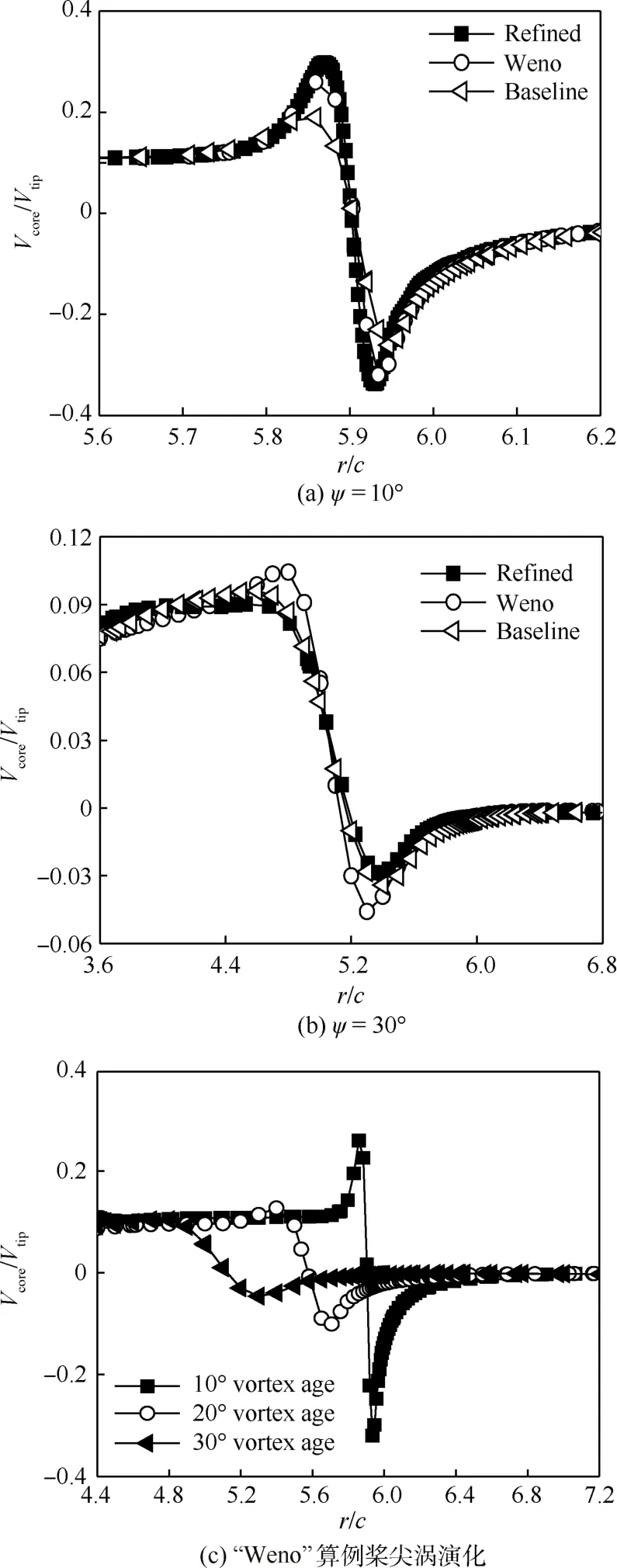
图11 3个涡龄角处桨尖涡的涡核速度截面Fig.11 Tip vortex core velocity profiles at three vortex ages

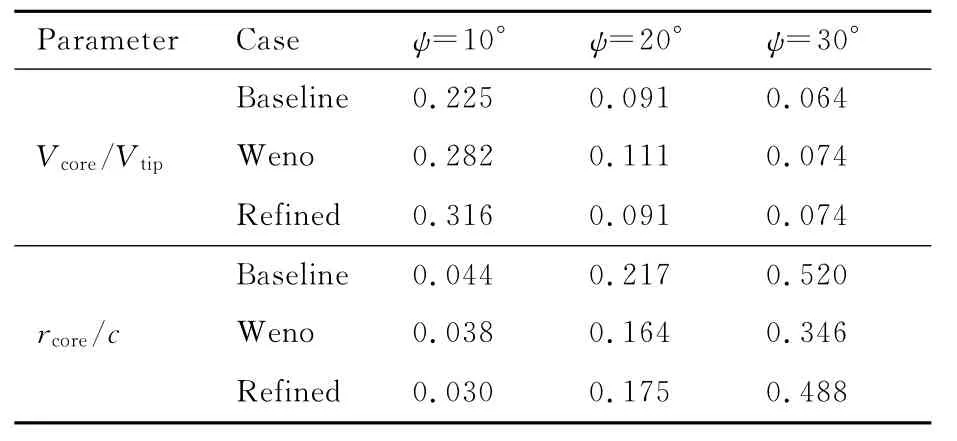
表1 涡核旋转速度和半径的演变规律Table 1 Evolutions of swirl velocity and radius of vortex core

然而经过一段距离的演化,在20°和30°涡龄角处,“Refined”算例的涡核速度很快降到与“Baseline”相近,而“Weno”算例的涡核速度下降最慢,并且在30°涡龄角处具有最大的涡核速度,如图11(b)所示。另外,涡核直径的演化规律与涡核速度具有高度的一致性,由此可见,5阶WENO计算格式在降低旋翼桨尖涡数值耗散方面具有较好的能力。然而,尽管如此,旋翼桨尖涡依然存在较强的数值耗散。图11(c)列出了“Weno”算例3个桨尖涡随涡龄角的变化规律,图中r/c为桨尖涡涡核的径向位置。由图可见,即便是采用5阶WENO计算格式,旋翼桨尖涡依然很快耗散,这说明旋翼桨尖涡在生成后经历了很强的物理耗散过程,因此,对于旋翼桨尖涡的生成捕捉计算,可不在桨叶网格上添加高阶计算格式,但必须对桨叶网格的相应部分进行加密,从而保证桨尖涡的捕捉精度。

3.2 旋翼桨尖涡演化规律分析

为了研究旋翼桨尖涡的演化规律,在不同桨尖马赫数和总距下对Caradonna-Tung旋翼的桨尖涡进行了参数化计算。如图12所示,选取不同计算状态下不同涡龄角处的旋翼桨尖涡截面,通过其涡核中心径向和垂向位置的变化分析旋翼桨尖涡下降和收缩特性随计算状态变化的规律。

图13给出了总距θ0=8°、桨尖马赫数Matip不同的各状态下Caradonna-Tung旋翼桨尖涡垂向位置y/c和径向位置r/c随涡龄角的变化曲线。观察图13(a)可见,在各桨尖马赫数下,旋翼桨尖涡从桨尖(r/c=6.0)处脱落后开始向旋转中心收缩,在收缩到r/c=4.8附近时,4个算例中的桨尖涡均开始向外扩张。对比4条曲线可见,桨尖马赫数小的算例中旋翼桨尖涡收缩速度更快,在达到收缩极限后也较先向外扩张。另外,由图13(b)可知,桨尖马赫数小的算例中旋翼桨尖涡下降速度也快,但由于其涡流场强度更小,其捕捉到的桨尖涡圈数也少。

图12 不同涡龄角处的桨尖涡截面Fig.12 Tip vortex profiles at different vortex ages

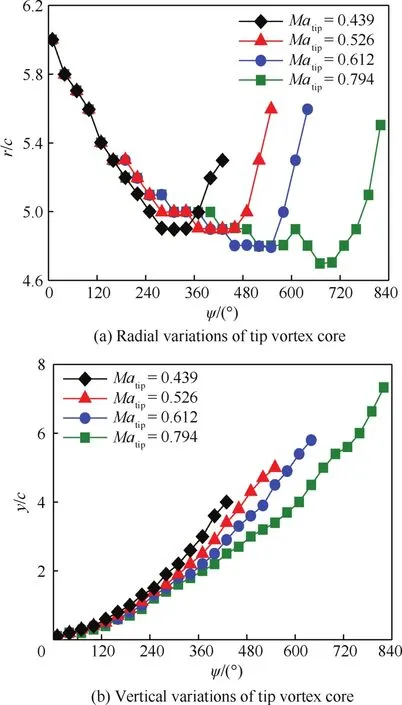
图13 不同桨尖马赫数下涡核位置的变化Fig.13 Position variations of tip vortex cores at different blade tip Mach number

图14是在0.3桨尖马赫数下,变换总距计算得到的旋翼桨尖涡演化曲线。如图14(a)所示,在不同总距的算例中,旋翼桨尖涡在收缩到r/c=4.8附近时开始向外扩张,这与图13(a)的结果是一致的。另外,由于0.3桨尖马赫数、4°总距状态的旋翼涡流场较弱且耗散较快,并没有捕捉到更多圈数,所以没有捕捉到其桨尖涡扩张现象。通过对比图14(a)和图14(b)可以发现,总距较大的算例中旋翼桨尖涡收缩和下降速度更快,捕捉到的桨尖涡圈数更多。

综合以上分析可知,对于本文计算的不同计算状态下的Caradonna-Tung旋翼桨尖涡,存在一个收缩极限使得旋翼桨尖涡收缩至此位置即开始向外侧扩张。收缩极限之所以存在,是因为在旋翼桨尖涡产生的初期其涡强度较大且没有较大的物理耗散,其诱导出的旋翼下洗流也较大,这就导致了桨盘下方内侧的气流速度(动压)高于外侧,内侧气流静压则小于外侧,所以大气压将桨尖涡向内侧挤压,而随着桨尖涡的演化和耗散,内侧气流速度下降,内外压差逐渐减小,桨尖涡则不再向内收缩而是向外侧扩张。另外从以上结果分析可知,旋翼桨尖马赫数越小、总距越大,桨尖涡的下降和收缩速度就越快。

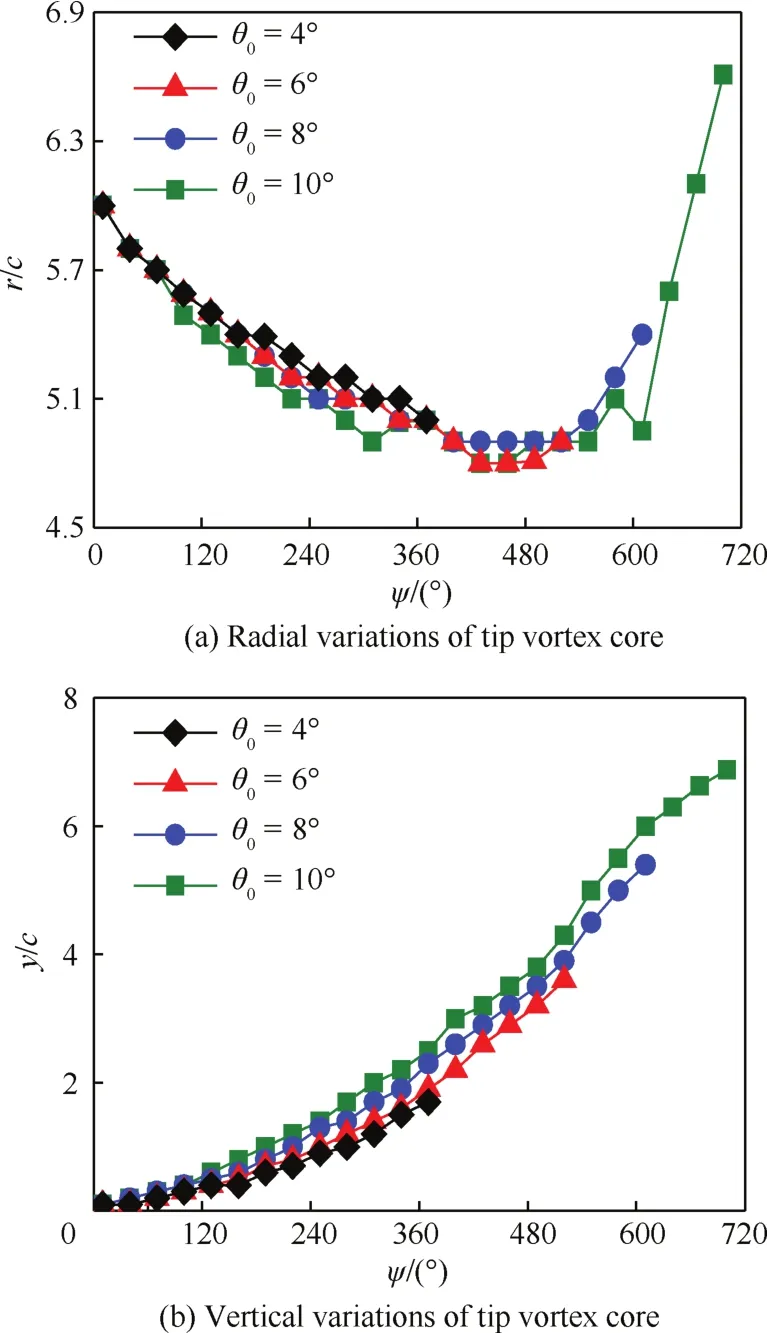
图14 不同总距下涡核位置的变化Fig.14 Position variations of tip vortex core at different collective pitch

4 结 论

本文建立了一个基于网格加密技术和5阶WENO计算格式的旋翼桨尖涡高精度CFD求解器。采用所建立的方法对旋翼桨尖涡流场进行了计算,细致地模拟了桨尖涡的形成和演化过程,研究结果表明:

1)在旋翼桨尖气流卷起至桨尖涡涡核能够清晰分辨时,桨尖涡下方会出现与桨尖涡旋转方向相反的二级涡,但该二级涡强度较低,在桨尖涡形成后即很快耗散殆尽。

2)在桨叶网格上,桨叶贴体网格加密措施能明显提高桨尖涡的捕捉精度,高阶 WENO格式则能一定程度上降低数值耗散。然而,旋翼桨尖涡在初始生成阶段存在较强的物理耗散,此耗散很难通过高阶格式和网格加密等措施来减弱。

3)对于本文计算的不同状态下的旋翼桨尖涡,存在一个收缩极限(约0.8R处)使得桨尖涡收缩到此位置后便开始向外扩张。此外,旋翼的桨尖马赫数越小、总距越大,桨尖涡的下降和收缩速度就越快。

4)本文建立的高精度求解器能有效地对旋翼桨尖的边界层增厚、桨尖涡的卷起和演化过程进行细致模拟,成功揭示了旋翼桨尖涡的生成及演化机理。

[1] HEINECK J T,YAMAUCHI G K,WADCOCK A J,et al.Application of three-component PIV to a hovering rotor wake[C]//Proceedings of the 56th AHS Annual Forum.Fairfax Virginia:American Helicopter Society,2000.

[2] MARTIN P B,LEISHMAN J G,PUGLIESE G J,et al.Stereoscopic PIV measurements in the wake of a hovering rotor[C]//Proceedings of the 56th AHS Annual Forum.Fairfax Virginia:American Helicopter Society,2000.

[3] WONG O D,KOMERATH N M.Tip vortex formation and evolution to the near wake of a rotor in forward flight[C]//Proceedings of the 57th AHS Annual Forum.Fairfax Virginia:American Helicopter Society,2001.

[4] RICHARD H,RAFFEL M.Rotor wake measurements:full-scale and model tests[C]//Proceedings of the 58th AHS Annual Forum.Fairfax Virginia:American Helicopter Society,2002.

[5] RAMASAMY M,JOHNSON B,LEISHMAN J G.Turbulent tip vortex measurements using dual-plane digital particle image velocimetry[C]//Proceedings of the 64th AHS Annual Forum.Fairfax Virginia:American Helicopter Society,2008.

[6] KINDLER K,MULLENERS K,RICHARD H,et al.A full-scale Particle Image Velocimetry investigation of“Young”rotor blade tip vortices[C]//Proceedings of the 65th AHS Annual Forum.Fairfax Virginia:American Helicopter Society,2009.

[7] DURAISAMY K,RAMASAMY M,BAEDER J D,et al.High resolution computational and experimental study of hovering rotor tip vortex formation[J].AIAA Journal,2007,45(11):2593-2602.

[8] 印智昭,招启军,王博.基于高阶WENO格式的旋翼非定常涡流场数值模拟[J].航空学报,2016,37(8):2552-2564.YIN Z Z,ZHAO Q J,WANG B.Numerical simulations for the unsteady vortex flowfield of rotors based on highorder WENO scheme[J].Acta Aeronautica et Astronautica Sinica,2016,37(8):2552-2564(in Chinese).

[9] 龚志斌,李杰,张恒.翼尖开孔吹气流动控制数值模拟研究[J].航空计算技术,2015,45(4):21-23.GONG Z B,LI J,ZHANG H.Numerical simulation of flow control over a fixed wing with slotted tip[J].Aeronautical Computing Technique,2015,45(4):21-23(in Chinese).

[10] 叶舟,徐国华,史勇杰.直升机旋翼/尾桨/垂尾气动干扰计算研究[J].航空学报,2015,36(9):2874-2883.YE Z,XU G H,SHI Y J.Computational research on aerodynamic characteristics of helicopter main-rotor/tail-rotor/vertical-tail interaction[J].Acta Aeronautica et Astronautica Sinica,2015,36(9):2874-2883(in Chinese).

[11] POMIN H,WAGNER S.Navier-Stokes analysis of helicopter rotor aerodynamics in hover and forward flight[J].Journal of Aircraft,2002,39(5):813-821.

[12] ROE P L.Approximate Riemann solvers,parameter vectors,and difference schemes[J].Journal of Computational Physics,1981,43(2):357-372.

[13] BORGES R,CARMONA M,COSTA B,et al.An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws[J].Journal of Computational Physics,2008,227(6):3191-3211.

[14] HARTEN A,ENGQUIST B,OSHER S,et al.Uniform-ly high order essentially non-oscillatory schemes[J].Siam Journal on Numerical Analysis,1987,115(1):200-212.

[15] BLAZEK J.Computational fluid dynamics:principles and applications[M].2nd ed.Oxford:Elsevier Ltd.,2007:274-276.

[16] LUO H,BAUM J D,LOEHNER R.A fast,matrix-free implicit method for computing low Mach number flows on unstructured grids[J].International Journal of Computational Fluid Dynamics,2000,14(2):133-157.

[17] BALDWIN B,LOMAX H.Thin layer approximation and algebraic model for separated turbulent flows[C]//Proceedings of the AIAA 16th Aerospace Sciences Meeting.Reston:AIAA,1978.

[18] CHIU I T,MEAKIN R L.On automating domain connectivity for overset grids:AIAA-1995-0854[R].Reston:AIAA,1995.

[19] THOMPSON J F,THAMES F C,MASTIN C W.Automatic numerical generation of body-fitted curvilinear coordinate system for field containing any number of arbitrary two-dimensional bodies[J].Journal of Computational Physics,1974,15(3):299-319.

[20] RENZONI P,D'ALASCIO A,KROLL N,et al.EROS-a common European Euler code for the analysis of the helicopter rotor flowfield[J].Progress in Aerospace Science,2000,36(5):437-485.

[21] CARADONNA F X,TUNG C.Experimental and analytical studies of a model helicopter rotor in hover:NASATM-81232[R].Washington,D.C.:NASA,1981.

[22] TANGLER J L.Experimental investigation of the subwing tip and its vortex structure:NASA-CR-3058[R].Washington,D.C.:NASA,1978.

High-resolution numerical research on formation and evolution mechanism of rotor blade tip vortex

YE Zhou,XU Guohua*,SHl Yongjie

National Key Laboratory of Science and Technology on Rotorcraft Aeromechanics,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

To capture the formation and evolution process of the helicopter blade tip vortex in detail,a computational fluid dynamics(CFD)method based on refined grids and a high-order interpolation scheme is presented.ln this method,the Navier-Stokes equation in the rotating coordinate system is selected as the governing equation.For spatial discretization,the upwind Roe scheme together with a fifth-order WENO(Weighted Essentially Non-Oscillatory)scheme is employed to calculate the convective variables.A dual-time method is utilized for time marching,and the implicit LU-SGS(Lower-Upper Symmetric Gauss-Seidel)scheme is adopted for every pseudo time step.The information between blade grid and the background grid is exchanged by using the overset grid method.With the method developed,the tip vortex flowfield of a hovering rotor is simulated accurately,and the detailed formation process and the evolution of the blade tip vortex are captured in the blade and background grids,respectively.The formation and evolution mechanisms of the blade tip vortex are then discussed.lt is demonstrated that the current high-accuracy method is effective in simulating the formation and evolution of the blade tip vortex in hover condition.The cross flow around the blade tip is firstly attached to the blade,and then the boundary layer grows due to the pressure gradient.With advancing downstream,the vortex core is gradually identifiable,and is detached from the tip blade ultimately.

blade tip vortex;WENO scheme;overset grid;computational fluid dynamics;rotor;helicopter

2016-10-13;Revised:2016-12-14;Accepted:2016-12-22;Published online:2017-02-16 09:36

URL:www.cnki.net/kcms/detail/11.1929.V.20170216.0936.002.html

s:National Natural Science Foundation of China(11302103);Funding of Jiangsu lnnovation Program for Graduate Education(KYLX15_0238);The Fundamental Research Funds for the Central Universities

V211.52

A

1000-6893(2017)07-520846-11

10.7527/S1000-6893.2017.120846

2016-10-13;退修日期:2016-12-14;录用日期:2016-12-22;网络出版时间:2017-02-16 09:36

www.cnki.net/kcms/detail/11.1929.V.20170216.0936.002.html

国家自然科学基金(11302103);江苏省研究生培养创新工程(KYLX15_0238);中央高校基本科研业务费专项资金

*通讯作者.E-mail:ghxu@nuaa.edu.cn

叶舟,徐国华,史勇杰.旋翼桨尖涡生成及演化机理的高精度数值研究[J].航空学报,2017,38(7):520846.YE Z,XU G H,SHl Y J.High-resolution numerical research onformation and evolution mechanism ofrotor blade tip vortex[J].Acta Aeronautica et Astronautica Sinica,2017,38(7):520846.

(责任编辑:鲍亚平)

*Corresponding author.E-mail:ghxu@nuaa.edu.cn