频率不变宽带波束形成权重系数的稀疏优化

张书瑞,马晓峰*,盛卫星,韩玉兵

南京理工大学 电子工程与光电技术学院,南京 210094

频率不变宽带波束形成权重系数的稀疏优化

张书瑞,马晓峰*,盛卫星,韩玉兵

南京理工大学 电子工程与光电技术学院,南京 210094

在基本的傅里叶变换频率不变波束形成(FIB)基础上,从减少抽头权重系数数量,降低FIB运算量角度出发,提出基于最小l0范数的抽头权重系数稀疏优化模型,并采用正交匹配追踪(OMP)算法来求解该优化问题。在高增益、等波纹、低旁瓣FIB方向图的要求下,所提出的优化方法使得稀疏率降低到3.53%,且能够保证稀疏优化后的方向图误差小于1%。接着进一步开展阵元数量的稀疏优化,有效地减少了阵元通道数,进一步降低了算法实现的硬件复杂度。仿真结果验证了所提方法的正确性和有效性。

相控阵;宽带信号处理;频率不变波束形成;稀疏优化;低复杂度

在雷达、通信、成像等领域中,系统宽带化和一体化是发展趋势。宽带雷达具有更强的抗干扰能力和更高的距离分辨率,可以获取更多的目标特征信息,同时,宽带系统也有利于雷达、通信和成像系统的多功能一体化集成。因此,宽带数字阵列天线的需求越来越迫切[1-5],开展低成本高效宽带数字波束形成技术的研究具有十分重要的理论价值和现实意义[6-9]。

空时联合优化结构常用于宽带阵列信号处理,这类方法所需的空时二维系数规模较大,迭代收敛速度慢,且单次迭代运算复杂。另外,空时联合优化方法需要预延时结构来实现波束指向控制,无论在模拟域还是数字域,延时误差均是不可避免的,这会造成宽带波束形成性能的严重下降[10-11]。空频联合优化方法也是宽带自适应阵列信号处理的主要研究方向[6,12],由于这类方法将时域信号转换到变换域上,再进行自适应阵列信号处理,计算量较大。

频域不变波束形成(Frequency Invariant Beamforming,FIB)能够有效地解决宽带波束形成频率不一致的问题,所以FIB是近年来宽带波束形成的研究热点。文献[6,13-14]提出了基于傅里叶变换的均匀线阵FIB,该结构与空时联合优化技术所采用的抽头延时结构相同,抽头权重系数的求解只需离散傅立叶逆变换(Inverse Discrete Fourier Transform,IDFT)和加窗处理即可。该方法实现简单,并且能够推广到多维阵列。文献[15]提出了基于子带分解的FIB,该方法将通带范围内的信号分解为相应子带进行窄带波束形成,然后利用最小二乘法实现FIB,由于该方法要进行信号子带分解,增加了计算复杂度。文献[16]利用最小二乘(Least Squares,LS)、线性约束(Constrained Least Squares,CLS)、无约束(Unconstrained Least Squares,ULS)和整体约束(Constrained Total Least Squares,CTLS)准则来计算FIB抽头权重系数。在不同准则约束下,优化目标均为不同频点方向图与参考频点方向图的均方误差最小。这些准则的优化目标直接,但得到的FIB方向图性能和选取参考方向图有很大的关系,计算复杂度较高;若要实现高增益、等波纹、低旁瓣等高要求的FIB方向图,权重计算复杂度会进一步提高,方向图的频域一致性也会恶化。

针对FIB的零陷干扰抑制问题,文献[17]利用固定角度方向零陷约束和等波纹原型滤波器,实现了零陷可控的低旁瓣FIB。同时,针对FIB的系数稀疏优化问题,文献[17]还提出了一种门限稀疏约束优化方法,但是,该方法难以确保方向图误差控制在可接受的范围内,且无法实现抽头延时线(Tapped Delay Lines,TDLs)的稀疏。文献[18]提出了基于压缩感知(Compressive Sensing,CS)的FIB稀疏理论,该文献将最小l0范数问题退化到最小l1范数上求解,由于约束条件放宽,基于最小l1范数求得的有效权重系数个数要大于基于最小l0范数的方法。另外该方法是利用文献[16]提出的FIB准则来计算未稀疏的抽头权重系数,计算复杂度高。

在高增益、等波纹、低旁瓣FIB方向图的要求下,方向图综合需要消耗大量的自由度,增加了稀疏优化的难度。本文在高增益、等波纹、低旁瓣的傅立叶变换FIB基础上,提出了求解基于最小l0范数抽头权重系数稀疏约束的优化模型,在FIB方向图恶化程度受控的前提下,实现了稀疏权重迭代过程的快速收敛,优化得到了稀疏表示的抽头权重系数。在此基础上,增加了抽头延时线的稀疏优化方法,该优化方法对各抽头延时线的可视期望信号增益进行判断,若不满足增益要求,优化方法会消除该抽头延时线的权重系数,即有效地减少了阵元通道(横向滤波器)数。本文所提出的稀疏优化方法实现简单,仿真结果也验证了本文方法的正确性和有效性。

1 高增益等波纹低旁瓣FIB

如图1所示,设均匀线阵含有M个各向同性的全向天线,阵元间距d取通带范围内最高频率对应波长的一半。采用如图2所示的空时抽头结构实现频率不变的高增益、等波纹、低旁瓣FIB,每个阵元后的横向滤波器阶数为K。

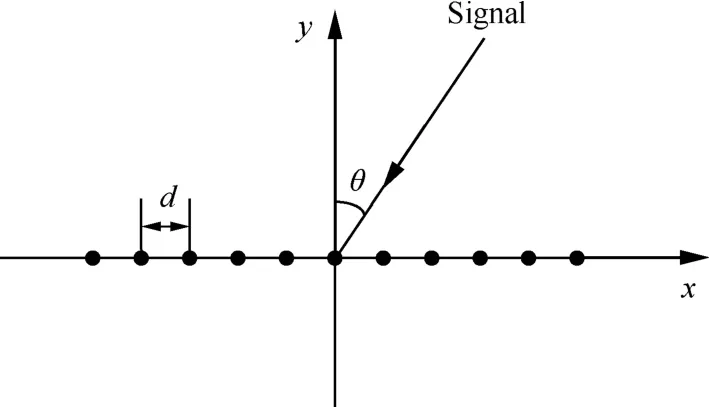
图1 均匀线阵示意图Fig.1 Equally spaced linear array

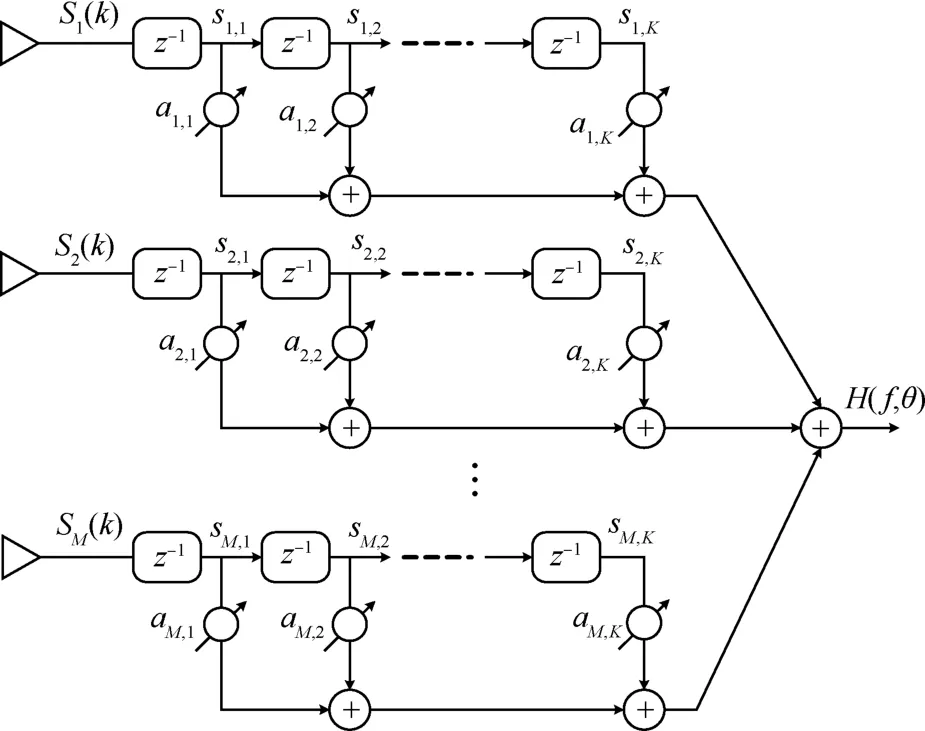
图2 频域不变波束形成结构Fig.2 Frequency invariant beamforming structure

设Sm(k)(m=1,2,…,M)为k时刻、第m个阵元接收到的信号,其表达式为

式中:c为光速;f为信号频率;θ为来波信号方向;Ts为采样周期;fs为采样频率。

定义am,k(m=1,2,…,M,k=1,2,…,K)为FIB抽头权重系数,那么FIB的方向图响应H(f,θ)可以表示为

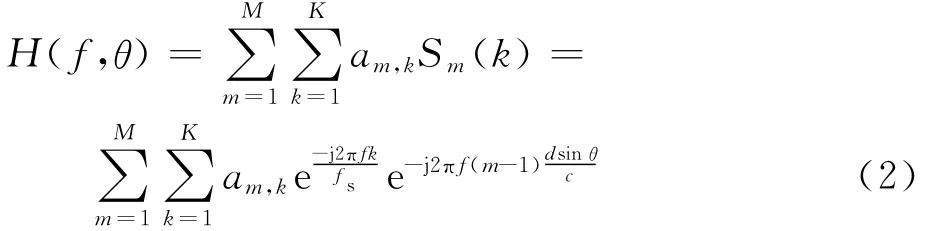
[6,14],定义F1=f/fs,F2=(df sinθ)/c,将其代入式(2)中,得到方向图函数G(F1,F2)关于F1和F2的表达式为

由式(3)可知,方向图函数G(F1,F2)与FIB抽头权重系数am,k满足二维离散傅立叶变换(Discrete Fourier Transform,DFT)对关系,即G(F1,F2)为am,k的二维频响特性。那么,只要使得G(F1,F2)与来波信号频率f无关,再对G(F1,F2)关于F1和F2进行二维逆离散傅立叶变换(Inverse DFT,IDFT),就能得到基于傅立叶变换的FIB抽头权重系数am,k。要使得波束方向图与频率无关,只与扫描角度有关,那么FIB的方向图频响特性应表示为

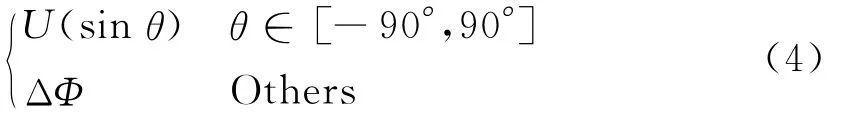
H(f,θ)=G(F1,F2)=一般地,ΔΦ=0°,U(sinθ)为只与波束指向角度有关的函数。由F1和F2的定义可知

文献[19]指出,时域低通FIR滤波器的频响特性与空域波束形成方向图具有对应的关系,那么式(4)中的U可以通过原型低通等波纹滤波器的频响特性来表征,这样就可以设计得到期望的高增益、等波纹、低旁瓣FIB方向图。

当波束指向法向0°时,相当于原型低通等波纹FIR滤波器的频响特性的归一化频率F=0。因为sinθ∈[-1,1],F∈[-0.5,0.5],并且要满足当F=0时,sinθ=0,根据文献[6,14],定义F=sinθ/2。同理,若波束指向偏离法向θ0时,原型低通FIR滤波器的频率响应就要在频率维上平移sinθ0/2,那么就有F=(sinθ-sinθ0)/2。因为波束指向法向(0°)和偏离法向(θ0)的分析方法相同,为了简化分析,后续仅考虑波束指向法向的情况,即F=sinθ/2。

已知X阶低通等波纹FIR滤波器的系数为p(x),且X一般为奇数。那么该低通等波纹FIR滤波器的频响特性P(F)表示为

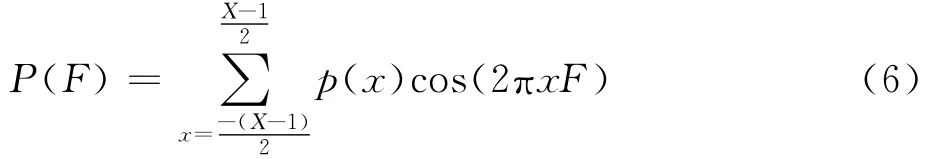
由F=sinθ/2,式(4)中的U(sinθ)可以表示为

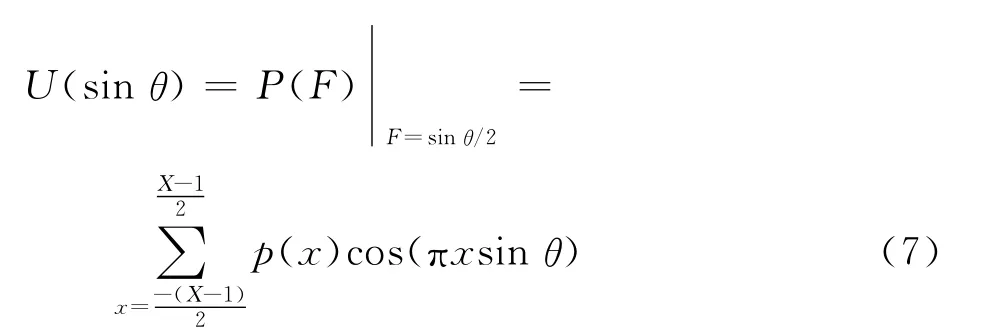
那么,高增益、等波纹、低旁瓣FIB的抽头权重系数am,k的计算步骤为

步骤1 将式(7)代入式(4),可得G(F1,F2)=

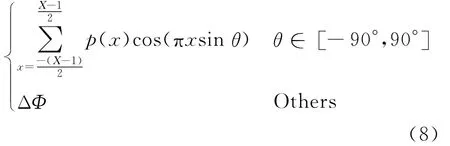
步骤2 对G(F1,F2)进行二维IDFT,求得q(n1,n2)。

步骤3 对q(n1,n2)在n1和n2维度上分别使用M点和K 点的窗函数进行加窗处理,从而求得高增益、等波纹、低旁瓣FIB的抽头权重系数am,k(m=1,2,…,M,k=1,2,…,K)。

2 基于稀疏优化的FIB

为了描述方便,对第1节给出的FIB表述进行重新建模。将通带范围内的宽带信号均分为I个子带,将空域扫描角度范围等间隔地分为J份,那么不同频率不同角度的来波信号S(f,θ)表示为

在式(9)～式(12)中,m=1,2,…,M,k=1,2,…,K。在式(12)中,sm,k(fi,θj)表示频率为fi(i=1,2,…,I)、来波方向为θj(j=1,2,…,J)的信号经过第m个阵元的第k个抽头延时后的数据。将第1节所求得的未稀疏FIB抽头权重系数

am,k(m=1,2,…,M,k=1,2,…,K)改写为向量形式a:

那么该FIB频响特性,即方向图响应可以描述为

式(15)给出了未稀疏FIB在不同频率下的方向图响应。接下来,定义稀疏FIB的权重系数向量w为

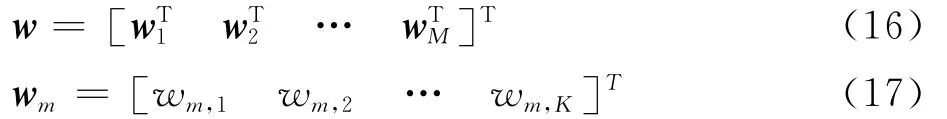
式中:wm,k为重新定义的第m个阵元的第k个抽头权重系数。若m=^m、k=^k位置的抽头权重系数经过稀疏优化后,为非有效系数,则w^m,^k=0。那么稀疏后的FIB方向图响应H～(f,θ)可以重新描述为

定义稀疏优化后FIB方向图的相对误差为

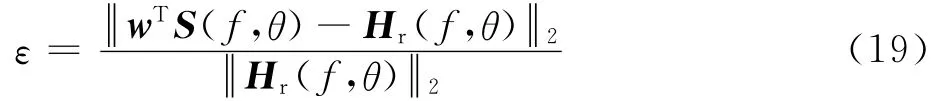
由式(19)方向图相对误差的定义可知,ε表示稀疏优化FIB方向图在主瓣区和旁瓣区与未稀疏FIB方向图的相对误差。该参数描述了稀疏优化FIB方向图与未稀疏FIB方向图相比的恶化程度。ε越小恶化程度越小。权重系数稀疏约束引入的目的是尽可能多的减少有效抽头权重系数的数量,且保证方向图误差在可接受的范围内。那么抽头权重系数稀疏优化问题就可以用式(20)来描述:

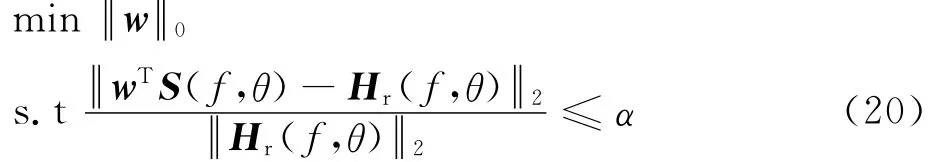
式中:w0为w的l0范数,即w中非零元素的个数;·2表示l2范数;α描述了稀疏优化方法允许方向图相对误差的最大值。

若式(20)中的信号为窄带信号(即I=1)、横向抽头滤波器的个数K=1,则该问题就退化为文献[20-21]中的窄带阵元稀布问题。本文利用文献[22]提出的正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法来求解式(20)的最小l0范数问题。OMP算法解决的是最小l0范数问题,它的基本思想是:以贪婪迭代的方法选择观测矩阵S(f,θ)的行,在每一次的迭代过程中,从完备原子库(即观测矩阵S(f,θ))中选择与方向图Hr(f,θ)最匹配的原子(即S(f,θ)的行),并将所选原子利用Gram-Schmidt正交化方法进行正交处理,再将Hr(f,θ)在这些正交原子构成的空间上投影,得到Hr(f,θ)在各个已选原子上的分量和余量,然后在剩余原子库中继续选出与Hr(f,θ)余量最为匹配的原子,经过数次迭代之后,当方向图相对误差足够小时(例如满足小于允许的最大相对误差α),Hr(f,θ)便可以由选出的原子线性表示,线性权重即为所要求的稀疏权重系数w。

对于抽头延时结构,式(20)只能在满足目标函数的条件下,实现对抽头权重系数的稀疏优化。为了实现对抽头延时线的稀疏优化,即将阵元通道数进一步减少,本文提出了抽头延时线的稀疏优化约束。其原理为,当该阵元后的抽头延时权重对主瓣范围Θs内信号的增益小于给定的抽头延时线稀疏阈值β时,将该抽头延时线上的权重系数全部置为0,即消除该抽头延时线。那么该抽头延时线稀疏优化约束表示为

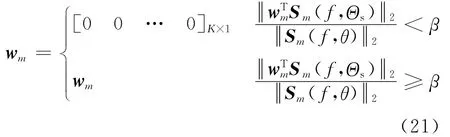
式中:m=1,2,…,M。

那么基于抽头权重系数稀疏和抽头延时线稀疏的宽带FIB稀疏优化方法的步骤可以描述为

步骤1 初始化:设置式(20)和式(21)中的α和β,余量H0=Hr(f,θ),迭代次数n=1,稀疏权重系数^w0=0MK×1,支撑集^S0=S(f,θ),并且为了描述方便,将支撑集分解为行向量表示的形式^S0=[S0(1) S0(2) … S0(MK)],索引集A=Ø。

步骤2 计算相关系数u=^Sn-1[Hn-1]T,将u中最大值对应的位置记录为λ(n),并将支撑集^Sn-1对应位置的向量记录为ˉS=Sn-1[λ(n)]。

步骤3 更新支撑集^Sn,将支撑集中对应的索引向量各元素置为0,即Sn[λ(n)]=[0 0 …0]1×IJ,并且更新索引集A=A∪ˉS。

步骤4 利用最小二乘法计算式(22),进行

权重逼近,求得W:

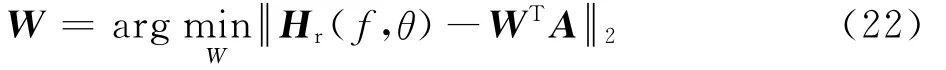
步骤5 得到第n次迭代的抽头稀疏系数^wn[λ(x)]=W(x),x=1,2,…,n。

步骤6 令w=^wn,通过式(21)进行抽头延时线是否稀疏的约束判断。

步骤7 若满足式(23),停止迭代;否则,通过式(24)求得余量Hn,令n=n+1,跳转到步骤2。

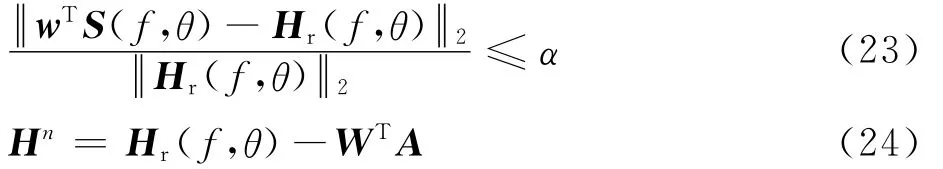
按照上述步骤,再结合第1节的内容,就可以得到基于抽头权重系数稀疏和抽头延时线稀疏的高增益、等波纹、低旁瓣FIB的稀疏权重系数。

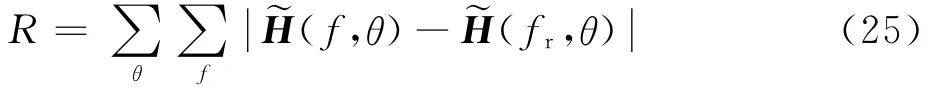
为了评价稀疏优化FIB方向图的一致性,参照文献[18],定义方向图频域一致性均方误差R为式中:fr为参考频率。在FIB的实际应用当中,需要确保通带范围内的方向图主瓣区保持一致,从而减少天线系统对宽带信号接收的失真影响;旁瓣区则只需要有较低的旁瓣特征即可。因此,式(25)中的积分求和范围为通带频率的主瓣区。

3 仿真分析

首先将给出原型低通等波纹FIR滤波器的频响特性,即期望的FIB方向图,并且给出未稀疏的高增益、等波纹、低旁瓣FIB的方向图;接着对本文提出的FIB稀疏方法进行仿真验证,并与文献[18]提出的基于最小l1范数稀疏约束的FIB和文献[17]所提出的基于门限约束的FIB进行性能比较和分析。

3.1 未稀疏FIB的方向图

为了得到高增益、等波纹、低旁瓣特性的频率不变方向图,原型低通等波纹FIR滤波器的阶数X=37,通过式(7)得到该原型滤波器的频响特性,即期望的FIB方向图。均匀线阵FIB的阵元间距为d=c Ts[13-14],阵元数M=59,横向滤波器阶数K=71,通带范围(归一化频率)为f/fs∈[0.3,0.5]。

由图3的归一化幅频响应可知,原型低通等波纹FIR滤波器的频响特性(即期望的方向图)的旁瓣电平为 -40 dB左右,3 dB波束宽度为4.1°。

由图4的未稀疏FIB不同频率下归一化方向图可知,基于傅立叶变换下FIB的3 d B波束宽度为4.1°左右、旁瓣电平为-40 dB,且能保持较高的频率一致性。

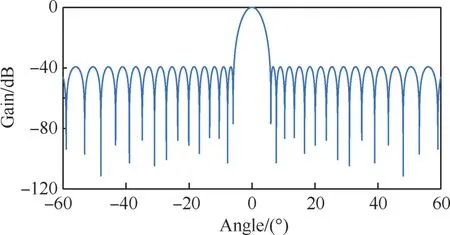
图3 原型滤波器归一化幅频响应Fig.3 Normalized frequency response of prototype filter

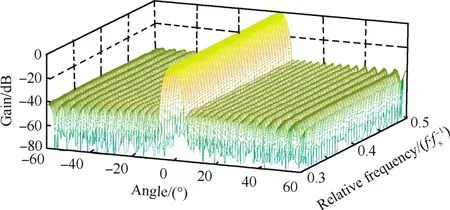
图4 未稀疏FIB的归一化方向图Fig.4 FIB beam pattern without sparse optimization

3.2 稀疏FIB的算法仿真和性能分析

在本文的稀疏优化算法中,稀疏后的FIB方向图允许的最大相对误差均为1%,即式(23)中的α=0.01。对于本文所提抽头延时线稀疏优化方法,式(21)中的β=2×10-5;主瓣区Θs为[-3°,3°]。其他仿真条件与3.1节相同。

对于本文所提算法,仿真分为两部分,一部分为只有基于最小l0范数的抽头权重系数稀疏约束,没有抽头延时线的稀疏约束;另一部分为在最小l0范数权重系数稀疏约束的基础上,加入抽头延时线的稀疏约束,即式(21)。

由图5和图6稀疏优化权重FIB的归一化方向图可知,拥有抽头延时线约束和不拥有抽头延

图5 抽头稀疏优化的FIB归一化方向图Fig.5 FIB beam pattern with proposed sparse design of taps

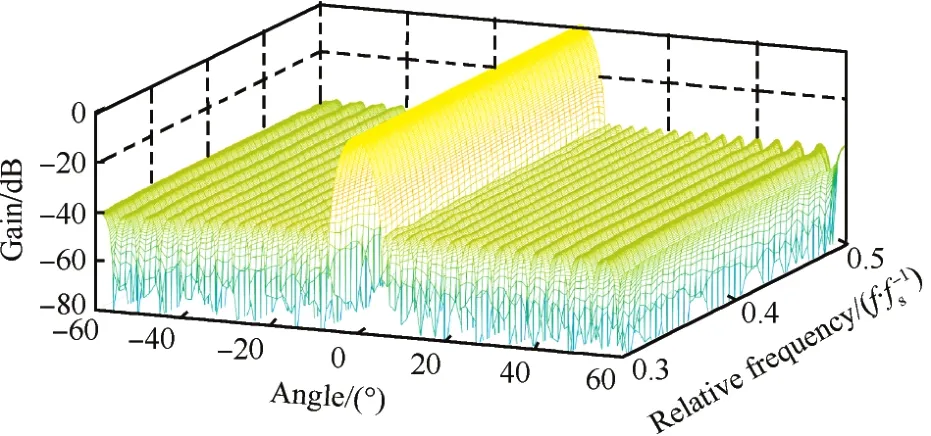
图6 抽头和延时线稀疏优化的FIB归一化方向图Fig.6 FIB beam pattern with proposed sparse design of taps and TDLs

图7 抽头稀疏优化后的有效抽头位置

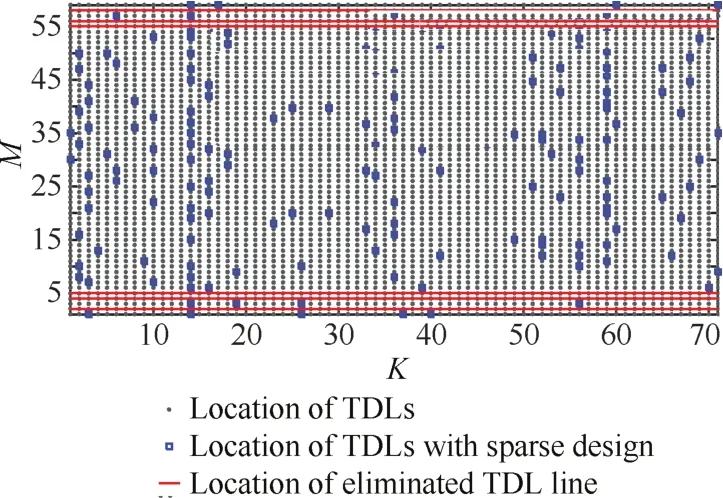
图8 抽头和延时线稀疏优化后的有效抽头和被消除延时线的位置Fig.8 Location of effective taps and eliminated TDLs with proposed sparse design of taps and TDLs

Fig.7 Location of effective taps with proposed sparse时线约束的FIB方向图均能够保持4.1°的3 dB主瓣宽度,并且能够实现-40 d B左右等波纹低旁瓣的要求。由图7和图8稀疏优化后的有效抽头位置可以看到,未添加抽头延时线稀疏约束的抽头阵列每一个通道均含有有效权重系数,接收通道数未减少,而添加抽头延时线稀疏约束的抽头阵列减少了6个阵列单元,有效的减少了接收通道数。

参照文献[18],求解基于最小l1范数的抽头权重系数稀疏约束,利用MATLAB的CVX工具箱来求解该优化问题,设置的迭代停止条件与本文方法相同,为稀疏后的FIB方向图相对误差小于1%。另外将文献[17]门限稀疏约束的门限设置为1.2×10-3,即若权重系数的绝对值小于约束门限时,该权重系数设置为0。其他仿真条件与3.1节相同。图9和图10将给出这两种稀疏约束方法的有效抽头位置。

图9 利用文献[18]理论稀疏优化后的有效抽头位置Fig.9 Location of effective taps with method in Ref.[18]

图10 利用文献[17]理论稀疏优化后的有效抽头位置Fig.10 Location of effective taps with method in Ref.[17]

由图9和图10可知,文献[17-18]所提出的稀疏约束方法能够减少抽头权重系数,但是有效抽头个数要大于本文所提出的方法,且每一个抽头延时线均含有有效权重系数,无法实现抽头延时线的稀疏。

表1给出了各个算法迭代次数、稀疏后的有效权重系数个数(稀疏率)、稀疏后方向图的相对误差、频率一致性以及阵元通道稀疏后对FIB性能影响的分析。与未稀疏方法相比,所有抽头权重系数稀疏算法均能够有效地减少抽头权重系数个数,其中基于最小l0范数无抽头延时线稀疏约束的FIB拥有最小的有效权重系数。与文献[18]的基于l1范数稀疏约束和文献[17]的门限稀疏约束相比,本文基于l0范数的稀疏约束能够大量地减少抽头权重系数。由式(19)计算不同稀疏方法的方向图相对误差,基于最小l1范数和本文所提方法均能够满足1%的方向图相对误差。由于基于约束门限的稀疏方法没有方向图误差约束,所以相较其他稀疏约束方法,其方向图相对误差较大。利用式(25),计算各个FIB的方向图一致性R,其中通带范围内的主瓣区Θs为[-3°,3°],归一化参考频率为fr/fs=0.4。相较未稀疏和其他稀疏方法,本文所提方法能够满足方向图一致性的要求,在通带范围内的主瓣区能够保证较好的方向图一致性,从图5和图7的不同频率下归一化方向图也可以得到相同的结论。

由表1还可知,抽头权重稀疏优化的迭代次数和有效权重个数是相同的。但是附带抽头延时线稀疏约束的优化方法有效权重个数是小于迭代次数的;并且,相较抽头权重稀疏优化方法,附带抽头延时线稀疏约束的优化方法需要更多的迭代次数,拥有更多的有效抽头权重个数。这是由于某几次迭代在步骤5中利用式(21)进行条件判断,置零了所得到的有效权重,需要重新寻找与Hr(f,θ)余量最为匹配的原子,造成了迭代步骤次数增加。从消除通道阵元数来说,只有本文所提基于最小l0范数抽头权重系数稀疏约束和抽头延时线稀疏约束能够在高增益、等波纹、低旁瓣的FIB要求下,有效地稀疏抽头数和通道数。

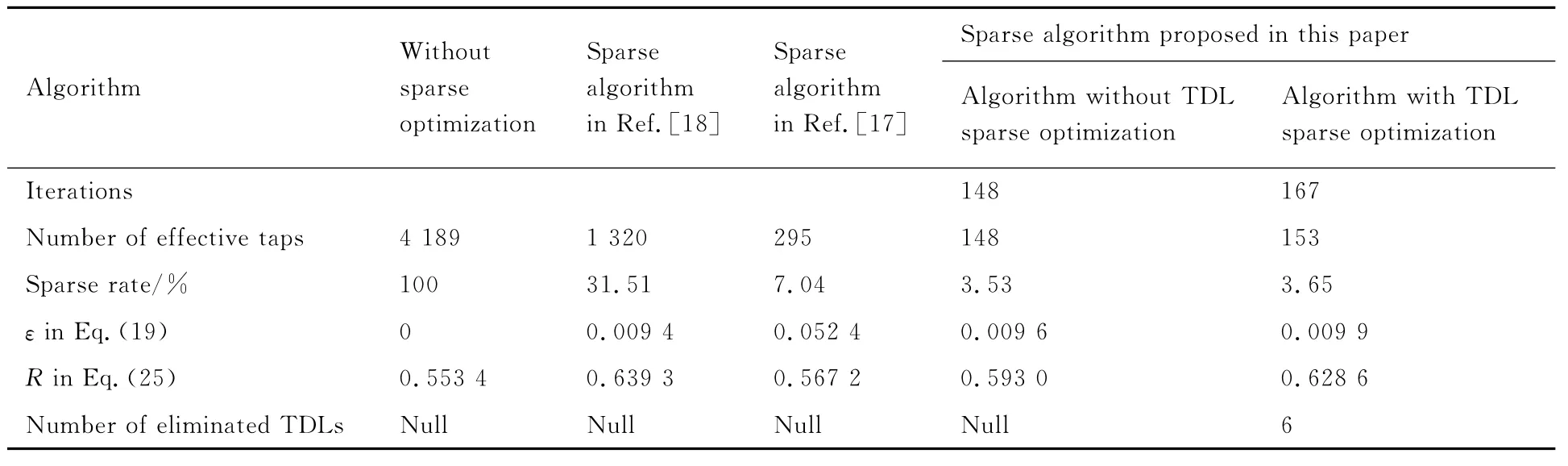
表1 不同算法的性能分析Table 1 Performance analysis of different algorithm

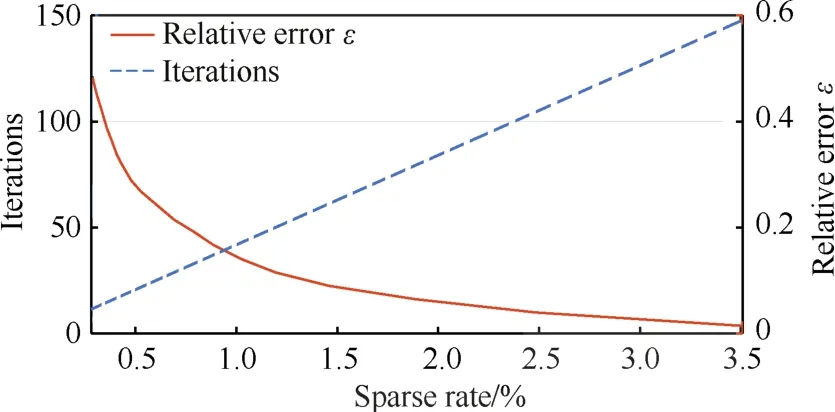
图11 稀疏率与算法性能的关系Fig.11 Relationship of sparse rate and algorithm performance

由图11可知,随着稀疏率的逐渐增加(即有效抽头个数的逐渐增多),本文所提算法的迭代次数逐渐增加,但稀疏优化方向图的相对误差逐渐减小。所以要得到较低的方向图相对误差,就要有较多的有效抽头权重个数(大的稀疏率),需要更多的算法迭代次数。

4 结 论

从降低FIB运算量的角度出发,本文提出了如下的稀疏优化方法。

1)提出了基于l0范数权重系数稀疏约束的优化模型和求解方法,确保方向图恶化在一定范围内的前提下,有效地实现FIB抽头延时权重系数的稀疏优化。

2)在1)基础上,增加了抽头延时线的稀疏约束,在有效稀疏抽头权重系数的同时,减少了阵元通道数,进一步降低了算法实现的硬件复杂度。

本文算法实现简单,有利于宽带阵列天线在低复杂度的情况下,实现高增益、等波纹、低旁瓣等高指标要求的FIB方向图。仿真结果验证了本文算法的正确性和有效性。

参 考 文 献

[1] NORDHOLM S,DAM H H H,LAI C C,et al.Broadband beamforming and optimization[J].Academic Press Library in Signal Processing,2014,3:553-598.

[2] SENAPATI A,GHATAK K,ROY J S.A comparative study of adaptive beamforming techniques in smart antenna using LMS algorithm and its variants[C]//2015 International Conference on Computational Intelligence and Networks(CINE),2015:58-62.

[3] GENG Z,DENG H,HIMED B.Adaptive radar beamforming for interference mitigation in radar-wireless spectrum sharing[J].IEEE Signal Processing Letters,2015,22(4):484-488.

[4] AHMAD F,ZHANG Y,AMIN M G.Three-dimensional wideband beamforming for imaging through a single wall[J].IEEE Geoscience and Remote Sensing Letters,2008,5(2):176-179.

[5] ZHAO Y,LIU W,LANGLEY R J.Adaptive wideband beamforming with frequency invariance constraints[J].IEEE Transactions on Antennas and Propagation,2011,59(4):1175-1184.

[6] LIU W,WEISS S.Wideband beamforming:concepts and techniques[M].New York:John Wiley&Sons,2010:143-198.

[7] BYRNE D,CRADDOCK I J.Time-domain wideband adaptive beamforming for radar breast imaging[J].IEEE Transactions on Antennas and Propagation,2015,63(4):1725-1735.

[8] CROCCO M,TRUCCO A.Design of superdirective planar arrays with sparse aperiodic layouts for processing broadband signals via 3D beamforming[J].IEEE/ACM Transactions on Audio,Speech,and Language Processing,2014,22(4):800-815.

[9] WEISS S,BENDOUKHA S,ALZIN A,et al.MVDR broadband beamforming using polynomial matrix techniques[C]//IEEE 23rd European Signal Processing Conference(EUSIPCO),2015:839-843.

[10] EBRAHIMI R,SEYDNEJAD S R.Elimination of presteering delays in space-time broadband beamforming using frequency domain constraints[J].IEEE Communications Letters,2013,17(4):769-772.

[11] EBRAHIMI R,SEYDNEJAD S R.Wideband Laguerre adaptive array with pre-steering constraints[J].IET Signal Processing,2015,9(7):529-536.

[12] SALLBERG B.Faster subband signal srocessing[dsp Tips&Tricks][J].IEEE Signal Processing Magazine,2013,30(5):144-150.

[13] SEKIGUCHI T,KARASAWA Y.Wideband beamspace adaptive array utilizing FIR fan filters for multibeam forming[J].IEEE Transactions on Signal Processing,2000,48(1):277-284.

[14] LIU W,WEISS S.Design of frequency invariant beamformers for broadband arrays[J].IEEE Transactions on Signal Processing,2008,56(2):855-860.

[15] ZHAO Y,LIU W,LANGLEY R J.Design of frequency invariant beamformers in subbands[C]//IEEE/SP 15th Workshop on Statistical Signal Processing,2009:201-204.

[16] ZHAO Y,LIU W,LANGLEY R J.Application of the least squares approach to fixed beamformer design with frequency-invariant constraints[J].IET Signal Processing,2011,5(3):281-291.

[17] 张书瑞,马晓峰,盛卫星,等.零陷可控的低旁瓣频率不变宽带波束形成[J].系统工程与电子技术,2016,38(6):114-120.ZHANG S R,MA X F,SHENG W X,et al.Wideband frequency beamforming with low sidelobes and anti-jamming nulls[J].Systems Engineering and Electronics,2016,38(6):114-120(in Chinese).

[18] HAWES M B,LIU W.Sparse array design for wideband beamforming with reduced complexity in tapped delaylines[J].IEEE/ACM Transactions on Audio,Speech,and Language Processing,2014,22(8):1236-1247.

[19] 王永良,丁前军,李荣锋.自适应阵列处理[M].北京:清华大学出版社,2009:13-61.WANG Y L,DING Q J,LI R F.Adaptive array processing[M].Beijing:Tsinghua University Press,2009:13-61(in Chinese).

[20] 王建,盛卫星,韩玉兵,等.基于压缩感知的自适应数字波束算法[J].电子与信息学报,2013,35(2):438-444.WANG J,SHENG W X,HAN Y B,et al.Adaptive digital beam forming algorithm based on compressed sensing[J].Jounal of Electronics&Information Technology,2013,35(2):438-444(in Chinese).

[21] WANG J,SHENG W X,HAN Y B,et al.Adaptive beamforming with compressed sensing for sparse receiving array[J].IEEE Transactions on Aerospace and Electronic Systems,2014,50(2):823-833.

[22] TROPP J A,GILBERT A C.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory,2007,53(12):4655-4666.

Sparse optimization for weight coefficient of wideband frequency invariant beamforming

ZHANG Shurui,MA Xiaofeng*,SHENG Weixing,HAN Yubing

School of Electronic and Optical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China

To reduce the computational complexity of the basic Fourier transform frequency invariant beamforming(FlB),the sparse optimization for tap weights of the FlB is proposed based on minimum l0norm.The optimization is solved by the orthogonal matching pursuit(OMP).,With the proposed method,the sparse rate of the effective tap weights decreases to 3.53%when the relative error of the FlB beam pattern is less than 1%.At the same time,the beam patterns of FlB synthesized by sparse tap weights can hold high gain,equiripple and low sidelobes.To reduce the number of tapped delay lines(TDLs),the sparse optimization for the TDLs is also presented,which effectively decreases the number of sensor elements,and reduces the implementation complexity.The simulation results verify the correctness and effectiveness of the proposed method.

phased array;wideband signal processing;frequency invariant beamforming;sparse optimization;low complexity

2016-09-18;Revised:2016-12-13;Accepted:2017-01-17;Published online:2017-01-19 08:27

URL:www.cnki.net/kcms/detail/11.1929.V.20170119.0827.002.html

s:National Natural Science Foundation of China(61401207);Key Projects Foundation of Shanghai Aerospace(SAST201437);College Graduate Scientific Research lnnovation Fund in Jiangsu Province of China(KYZZ16_0187)

TN958.92

A

1000-6893(2017)07-320794-09

10.7527/S1000-6893.2017.320794

2016-09-18;退修日期:2016-12-13;录用日期:2017-01-17;网络出版时间:2017-01-19 08:27

www.cnki.net/kcms/detail/11.1929.V.20170119.0827.002.html

国家自然科学基金(61401207);上海航天基金重点项目(SAST201437);江苏省研究生培养创新工程(KYZZ16_0187)

*通讯作者.E-mail:maxiaofeng@njust.edu.cn

张书瑞,马晓峰,盛卫星,等.频率不变宽带波束形成权重系数的稀疏优化[J].航空学报,2017,38(7):320794.ZHANG S R,MA X F,SHENG W X,et al.Sparse optimizationfor weight coefficient of wideband frequency invariant beamforming[J].Acta Aeronautica et Astronautica Sinica,2017,38(7):320794.

(责任编辑:苏磊)

*Corresponding author.E-mail:maxiaofeng@njust.edu.cn