金属梯度多孔夹芯板振动特性分析
2017-11-22肖登宝赵桂平
肖登宝, 赵桂平
西安交通大学 航天航空学院 机械结构强度与振动国家重点实验室, 西安 710049
金属梯度多孔夹芯板振动特性分析
肖登宝, 赵桂平*
西安交通大学 航天航空学院 机械结构强度与振动国家重点实验室, 西安 710049
金属梯度多孔材料芯层的胞孔壁厚度及半径沿芯层厚度方向逐渐变化,使得芯层的材料参数如密度和弹性模量等逐渐变化;采用金属梯度多孔材料代替传统均质多孔芯层会影响夹芯板的振动特性。基于高阶夹芯板理论且考虑梯度多孔芯层密度和弹性模量的耦合影响,建立了复合材料面层-金属梯度多孔夹芯板的振动方程。分析了3种密度的梯度芯层:单向分布、正梯度对称分布和负梯度对称分布对夹芯板固有频率的影响;最后讨论了3种梯度夹芯板在相同三角脉冲载荷作用下的振动响应。计算结果表明梯度芯层密度对称分布的夹芯板固有频率大于单向分布的夹芯板固有频率。
金属梯度多孔材料; 夹芯板; 高阶板理论; 振动特性; 脉冲载荷
复合材料夹芯结构的面层通常由高密度、高刚度的各向异性薄板组成,芯层由轻质均匀多孔材料或梯度多孔材料组成。面层承受切向载荷和弯矩,芯层承受横向剪切和垂直载荷。由于力学性能优越,复合材料夹芯结构已经广泛应用于飞机和高超声速飞行器。
近年来,国内外学者对梯度材料进行了许多研究。梯度材料可分为两种类型:功能梯度材料和梯度多孔材料。功能梯度材料通过改变各组分材料沿厚度方向的含量分布,使得材料在空间位置上呈现梯度变化,从而获得沿厚度方向逐渐变化的力学性能。目前对功能梯度芯层夹芯结构的振动特性研究已有许多成果[1-4]。在这些研究中,功能梯度材料芯层密度和弹性模量沿厚度方向的分布通常采用指数或幂函数描述,且二者之间相互独立。梯度多孔材料一般是孔壁厚度或孔径沿厚度方向逐渐变化,使得芯层的材料参数如密度和弹性模量等也沿厚度方向逐渐变化。Gibson和Ashby[5]基于相关实验数据分析并构建正方体模型模拟闭孔泡沫材料的受力性能,认为多孔材料的密度和弹性模量不是相互独立的。因而继续采用分析功能梯度材料的方法描述梯度多孔材料的密度和弹性模量分布是不可行的。Ashby[6]通过对理论模型的推导,给出了一个二次项函数来描述密度和弹性模量之间的耦合关系。但是在Ashby给出的公式中有需要根据研究者经验取值的参量,这制约着该公式的进一步应用。谢兰生等[7]采用十四面体结构模型(Kelvin结构模型[8-9])研究了泡沫金属弹性常数与其基体材料性能之间的关系。王嵩和卢子兴[10]采用Voronoi分析了泡沫材料相对密度对弹性性能的影响。Xiao等[11]通过对Gibson和Ashby[5]理论模型和实验数据的深入分析,给出了一个描述金属多孔材料弹性模量和密度之间耦合关系的多项式函数,并且进一步将该公式发展用来描述金属梯度多孔材料弹性模量分布与密度分布函数之间的耦合关系。
梯度多孔芯层材料对夹芯结构振动特性的影响,目前较少有学者做过分析。Rahmani等[12]给出了一个适用于梯度多孔芯层夹芯结构的高阶理论,在该模型中梯度芯层的密度是常量,弹性模量随厚度方向逐渐变化。Liu等[13]采用一阶剪切变形理论和高阶位移场理论来分别描述面板和梯度芯层的变形,建立了梯度芯层夹芯板的振动模型。在该模型中,密度和弹性模量是相互独立的。Xiao等[11]采用高阶夹芯板理论,获得了梯度多孔芯层夹芯板的振动方程,该模型中密度和弹性模量相互耦合;同时分析了密度线性分布的梯度多孔芯层夹芯板固有频率的特性。研究结果表明考虑芯层密度和弹性模量耦合的夹芯板固有频率随梯度范围的增加而降低,这与考虑芯层密度和弹性模量相互独立的夹芯板固有频率特性相反。因此在分析梯度多孔芯层夹芯板振动特性时必须考虑芯层密度和弹性模量的相互耦合。目前对于梯度多孔芯层密度非线性分布的夹芯板振动特性研究还较少,需要进一步深入研究。
本文给出了适用于梯度多孔夹芯板的振动方程,重点分析了3种金属梯度多孔芯层(单向分布、正梯度对称分布和负梯度对称分布)对夹芯板固有频率的影响。同时也讨论了这3种金属梯度多孔夹芯板受到相同冲击载荷作用时的振动响应,并比较研究了它们的变化特点,为梯度多孔夹芯板的设计提供理论依据。
1 金属梯度多孔夹芯板振动方程的建立
应用在飞机副翼上的夹芯结构,其沿翼展方向的几何尺寸远大于其他两个方向尺寸,为简化计算,可以将其等效为平面应变问题处理,如图1所示。图1所示的3种梯度多孔芯层分别是单向分布、正梯度对称分布和负梯度对称分布。其中正梯度对称分布型是指芯层密度分布关于x轴对称,同时密度由芯层中心面向其上下面逐渐增加;负梯度对称分布则反之。
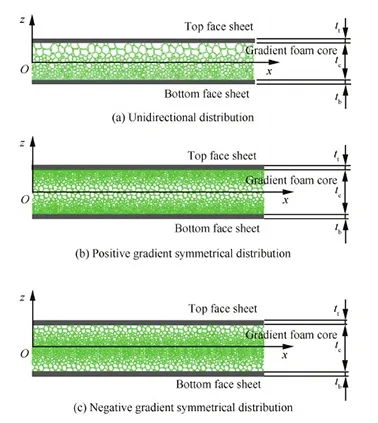
图1 金属梯度多孔芯层夹芯板示意图Fig.1 Schematic diagram of sandwich panel with gradient metallic cellular core
在模型中tt和tb分别表示上下面层厚度,tc表示芯层厚度,夹芯板的长度为l。模型基本假设:① 复合材料面层很薄刚度很大,承受切向载荷和弯矩,遵循Kirchhoff假设;② 金属泡沫芯层刚度较弱,承受横向正应力和剪切应力,具有横向压缩和剪切特性;③ 不考虑金属泡沫夹芯结构的缺陷,认为面层和芯层理想粘接。采用与厚度方向有关的2级幂级数描述芯层沿x的位移;采用与厚度方向有关的1级幂级数描述芯层沿z方向的位移。模型满足芯层和面层交界处位移连续条件。
上面层的位移场表示为
(1)
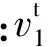
下面层的位移场表示为
(2)
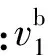
中间芯层的非线性高阶位移场表示为[14]
(3)
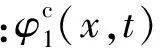
(4)
将式(1)~式(4)代入哈密尔顿方程中:

(5)
式中:δT为动能的变分形式;δU为应变能的变分形式;δW为虚功的变分形式。相比z方向动能,整个结构x方向的动能可以忽略,因此δT可写为
(6)
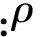
应变能变分δU可表达为
(7)
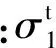
(8)
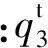
(9)
式中:质量矩阵各个元素详细附录参见文献[11]。
2 金属梯度多孔芯层的密度和弹性模量的耦合关系
金属梯度多孔芯层密度分布分为3种:单向分布、正梯度对称分布和负梯度对称分布。分布函数分别为
(10a)
(10b)
(10c)
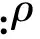
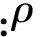

表1 梯度多孔芯层下面层的密度Table 1 Mass density of bottom face on gradient cellular core
图2 金属梯度多孔芯层密度沿厚度方向的分布 Fig.2 Mass density distribution of gradient metallic cellular core varies along thickness direction
金属梯度多孔芯层取梯度泡沫铝,其弹性模量和密度的耦合关系为[11]
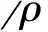
(11)
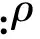
将式(10)和式(11)代入振动方程式(9)即可得到适用于分析金属梯度多孔芯层夹芯板的振动方程。面层的材料参数为
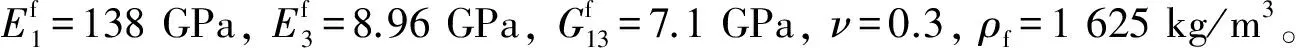
3 芯层密度梯度变化对夹芯板振动特性的影响
3.1 振动方程可靠性验证
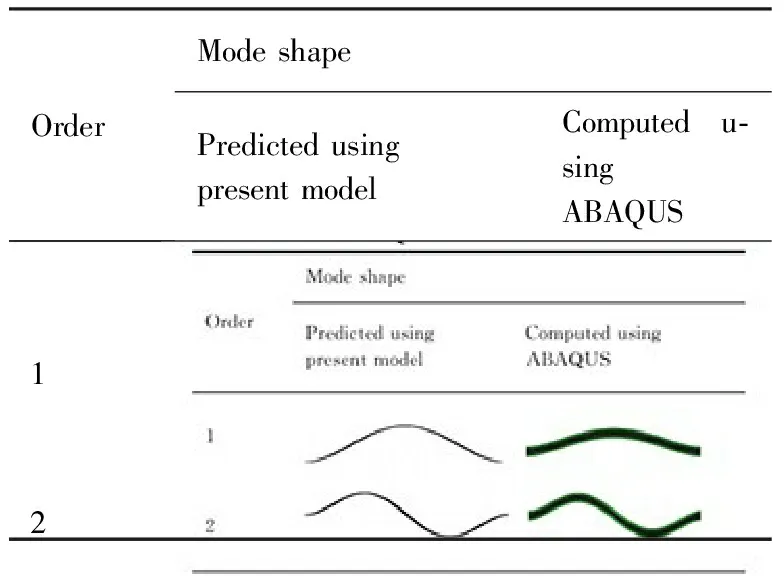
通过对比本文振动方程和ABAQUS软件计算的梯度泡沫夹芯板固有频率和相应振型,从而验证本文理论模型的可靠性。取梯度泡沫芯层的密度分布函数为式(10a),n=1,证明本文理论模型的可信性可靠性。夹芯板的固有频率详细附录参见文献[11],前2阶振型如表2所示。通过振型对比可以看出本文理论模型计算的振型和ABAQUS计算的振型一致。
表2梯度夹芯板理论和ABAQUS计算的前2阶振型对比
Table2ComparisonofthefirstsecondmodeshapescomputedusinggradientsandwichtheoryandABAQUS
OrderModeshapePredictedusingpresentmodelComputedu⁃singABAQUS12
3.2 芯层密度梯度变化对夹芯板固有频率的影响
金属梯度多孔芯层夹芯板第1、2阶固有频率随芯层密度梯度指数的变化如图3所示;金属梯度多孔芯层夹芯板的第1、2阶固有频率如表3所示。
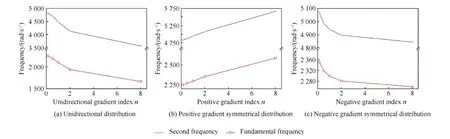
图3 金属梯度多孔夹芯板第1、2阶固有频率随梯度指数的变化Fig.3 Fundamental and second frequencies of sandwich panels vary with gradient index n
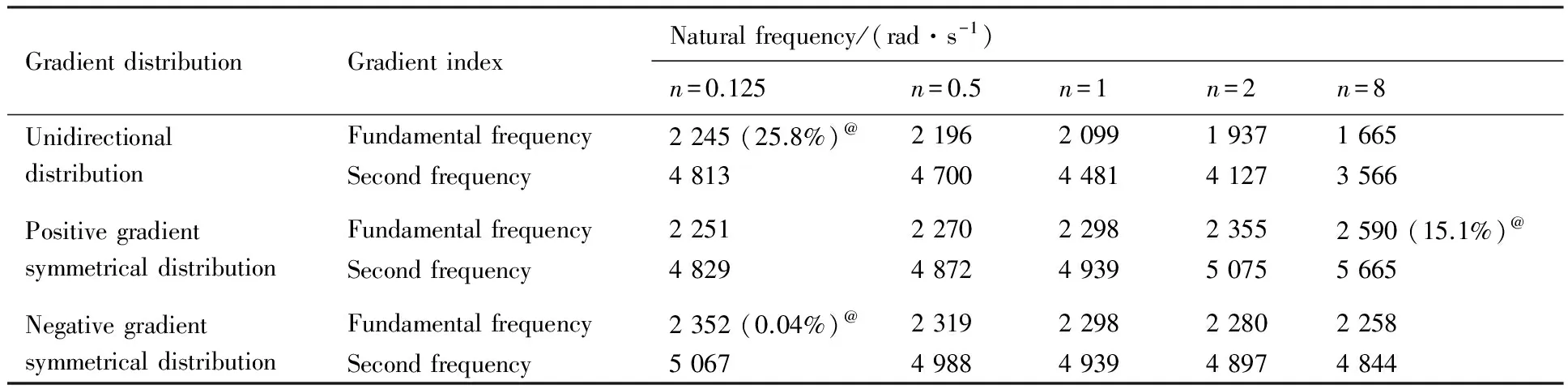
表3 金属梯度多孔芯层夹芯板第1、2阶固有频率Table 3 Fundamental and second frequencies of sandwich panels with gradient metallic cellular core
Note: @ represents relative error, i.e., (Maximum value of frequency-Minimum value of frequency)/Maximum value of frequenc×100%
从图3(a)中可以看到单向分布梯度夹芯板的第1、2阶固有频率随梯度指数的增加而降低;图3(b)正梯度对称分布夹芯板第1、2阶固有频率随梯度指数的变化近似线性变化;图3(c)中负梯度对称分布夹芯板的第1、2阶固有频率随梯度指数的增加而降低。
从表3中可以看出:在本文给出的n值范围内,芯层密度梯度对称分布的夹芯板固有频率明显大于单向分布的夹芯板固有频率。另外,对单向分布梯度夹芯板,不同的梯度指数分布情况下第1阶固有频率的最大值和最小值的相对差值为25.8%,由此可见改变单向分布的梯度指数对单向分布金属梯度多孔芯层夹芯板固有频率有较大的影响。但是,负梯度对称分布夹芯板的第1阶固有频率最大值和最小值之间的相对差值仅为0.04%,说明负梯度对称分布梯度夹芯板固有频率受梯度分布变化的影响非常小。
3.3 脉冲激励下芯层密度梯度变化对夹芯板最大挠度的影响
对两端固支夹芯板上面层施加均布的三角脉冲载荷, 其表达式为
(12)
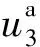
从图4(b)可以看出单向梯度芯层夹芯板的最大挠度随梯度指数的增加而增加,同时挠度衰减速度随梯度指数的增加而降低。
从图5中可以看出当梯度指数n<1时,负梯度对称分布芯层夹芯板的最大挠度值小于其他两种梯度分布夹芯板的最大值;当梯度指数n>1时,正梯度对称分布芯层夹芯板的最大挠度值小于其他两种梯度分布夹芯板的最大值。因此,夹芯板芯层的梯度模式和梯度指数对其振动的最大挠度有较大影响,在工程应用中要根据实际需要选择合适的梯度模式和梯度指数。
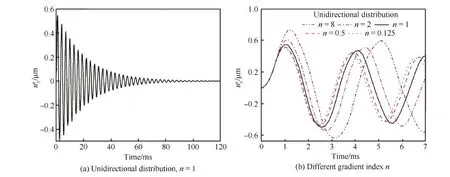
图4 单向金属梯度多孔夹芯板的振动特性Fig.4 Vibration response of sandwich panels with unidirectional distribution cellular core
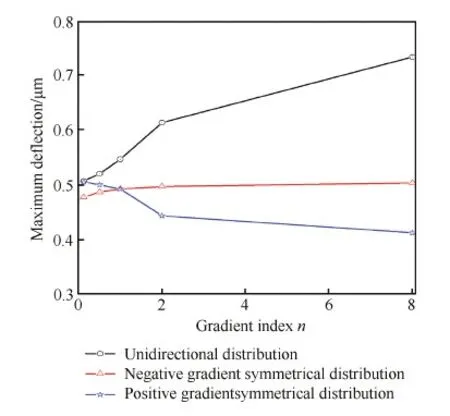
图5 3种梯度多孔芯层夹芯板的最大挠度Fig.5 Maximum deflections of sandwich panels with three gradient metallic cellular cores
4 结 论
针对金属梯度多孔夹芯板,采用高阶夹芯板理论同时考虑金属梯度多孔芯层弹性模量和密度的耦合作用得到金属梯度多孔芯层夹芯板的振动方程。在此基础上分析了金属梯度多孔芯层密度单向分布、正梯度对称分布、负梯度对称分布对夹芯板固有频率特性和振动响应的影响。结论如下:
1) 梯度指数变化对单向分布夹芯板固有频率影响最大,负梯度对称分布夹芯板固有频率受梯度分布变化的影响最小。另外在本文给出的密度梯度n值范围内,梯度芯层密度对称分布的夹芯板固有频率大于单向分布的夹芯板固有频率。
2) 当梯度指数n<1时,负梯度对称分布芯层夹芯板的最大挠度值小于其他两种梯度分布夹芯板的最大值;当着梯度指数n>1时,正梯度对称分布芯层夹芯板的最大挠度值小于其他两种梯度分布夹芯板的最大值。
本文结果为金属梯度多孔夹芯结构的设计提供了理论依据,可供工程应用参考。
[1] SURESH S, MORTENSEN A. Fundamentals of functionally graded materials[M]. London: IOM Communications Limited, 1998: 1-40.
[2] DAI H T, CHENG W, LI M Z. Static/dynamic analysis of functionally graded and layered magneto-electro-elastic plate/pipe under Hamiltonian system[J]. Chinese Journal of Aeronautics, 2008, 21(1): 35-42.
[3] 贺尔铭,胡亚琪,张钊,等. FGM板三维层合模型及热-噪声载荷下的动态响应研究[J]. 航空学报, 2013, 34(6): 1293-1300.
HE E M, HU Y Q, ZHANG Z, et al. 3-D laminated model and dynamic response analysis of FGM panels in thermal-acoustic environments[J]. Acta Aeronautica et Astronautica Sininca, 2013, 34(6): 1293-1300 (in Chinese).
[5] GIBSON L J, ASHBY M F. Cellular solids: Structure and properties[M]. 2nd ed. Cambridge: Cambridge University Press, 1997: 185-196.
[6] ASHBY M F. Metal foams: A design guide[M]. Oxford: Butterworth-Heinemann, 2000: 53-54.
[7] 谢兰生, 童国权, 高霖. Kelvin结构开孔泡沫材的弹性性能研究[J]. 应用力学学报, 2007, 24(1): 75-78.
XIE L S, TONG G Q, GAO L.Elastic properties of the Kelvin type with open-cells[J]. Chinese Journal of Applied Mechanics, 2007, 24(1): 75-78 (in Chinese).
[8] THOMOSON W S. On the division of space with minimum partitional area[J]. Acta Mathematica, 1887, 11(1): 121-134.
[9] 卢子兴, 黄纪翔, 陈鑫. 各向异性Kelvin开孔泡沫模型的弹性性能[J]. 航空学报, 2009, 30(6): 1017-1022.
LU Z X, HUANG J X, CHEN X. Elastic properties of anisotropic Kelvin model for open-cell foams[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(6): 1017-1022 (in Chinese).
[10] 王嵩, 卢子兴. 闭孔Voronoi泡沫的弹性性能分析 [J]. 航空学报, 2007, 28(3): 574-578.
WANG S, LU Z X. Investigation into elastic properties of closed-cell Voronoi foam[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(3): 574-578 (in Chinese).
[11] XIAO D B, MU L, ZHAO G P. The influence of correlating material parameters of gradient foam core on free vibration of sandwich panel[J]. Composites Part B: Engineering, 2015, 77: 153-161.
[12] RAHMANI O, KHALILI S M R, MALEKZADEH K, et al. Free vibration analysis of sandwich structures with a flexible functionally graded syntactic core[J]. Composite Structure, 2009, 91(2): 229-235.
[13] LIU M, CHENG Y S, LIU J. High-order free vibration analysis of sandwich plates with both functionally graded face sheets and functionally graded flexible core[J]. Composite Part B: Engineering, 2015, 72: 97-107.
[14] HOHE J, LIBRESCU L, OH S Y. Dynamic buckling of flat and curved sandwich panels with transversely compressible core[J]. Composite Structure, 2006, 74(1): 10-24.
[15] QIN Z, BATRA R C. Local slamming impact of sandwich composite hulls[J]. International Journal of Solids and Structures, 2009, 46(10): 2011-2035.
(责任编辑: 徐晓)
Vibration response of sandwich panels with gradient metalliccellular core
XIAODengbao,ZHAOGuiping*
StateKeyLaboratoryforStrengthandVibrationofMechanicalStructures,SchoolofAerospace,Xi’anJiaotongUniversity,Xi’an710049,China
The gradient metallic cellular material has gradient pore structures from one surface of the material to the other one resulting in varying material properties,such as mass density and elastic modulus. The vibration response of sandwich panels may be influenced when the traditional homogeneous cellular core is replaced by gradient metallic cellular core. Based on the high-order plate theory and considering the coupling effect between the density and the elastic module of gradient metallic cellular materials, the vibration equation for the sandwich panel with composite face sheet and gradient metallic cellular core is developed. The influence of three gradient types of cores (unidirectional distribution, positive gradient symmetrical distribution and negative gradient symmetrical distribution) on the natural frequency of sandwich panels is discussed. The vibration responses of sandwich panels with three gradient metallic cellular cores under the same impulsive loading are discussed.
gradient metallic cellular material; sandwich panel; high-order plate theory; vibration response; impulse load
2016-06-30;Revised2016-09-05;Accepted2016-12-27;Publishedonline2017-02-171322
URL:www.cnki.net/kcms/detail/11.1929.V.20170217.1322.008.html
NationalNaturalScienceFoundationofChina(11372237)
2016-06-30;退修日期2016-09-05;录用日期2016-12-27; < class="emphasis_bold">网络出版时间
时间:2017-02-171322
www.cnki.net/kcms/detail/11.1929.V.20170217.1322.008.html
国家自然科学基金 (11372237)
*
.E-mailzhaogp@mail.xjtu.edu.cn
肖登宝, 赵桂平. 金属梯度多孔夹芯板振动特性分析J. 航空学报,2017,38(6):220576.XIAODB,ZHAOGP.VibrationresponseofsandwichpanelswithgradientmetalliccellularcoreJ.ActaAeronauticaetAstronauticaSinica,2017,38(6):220576.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.220576
V214.8; O327
A
1000-6893(2017)06-220576-08
*Correspondingauthor.E-mailzhaogp@mail.xjtu.edu.cn
