基于充气前缘技术的旋翼翼型动态失速抑制

许和勇， 邢世龙， 叶正寅， 马明生,2

1.西北工业大学 翼型叶栅空气动力学国家级重点实验室， 西安 710072 2.中国空气动力研究与发展中心， 绵阳 621000

基于充气前缘技术的旋翼翼型动态失速抑制

许和勇1,*， 邢世龙1， 叶正寅1， 马明生1,2

1.西北工业大学 翼型叶栅空气动力学国家级重点实验室， 西安 710072 2.中国空气动力研究与发展中心， 绵阳 621000

动态失速的发生会在直升机旋翼桨叶和桨毂上产生高的交变扭转振动载荷，并限制直升机高速重载状态下的使用包线。本文利用计算流体力学(CFD)方法对基于充气前缘(ILE)技术的SC1095旋翼翼型动态失速抑制进行研究，分析了ILE抑制动态失速的控制机理，获得了ILE结构布置和充放气方式对动态失速的影响规律。研究表明：ILE可以有效抑制动态失速的发生；ILE最大膨胀程度越大，其抑制动态失速的效果越好，但膨胀程度过大后抑制效果开始减弱；ILE在翼型上仰至最大迎角时恰好达到最大膨胀状态，其对动态失速的抑制效果最好；ILE保持最大膨胀状态的时间长短对抑制效果影响不大；在翼型上仰至不同迎角时开始对ILE充气会对动态失速抑制有较大影响；ILE整流段与翼型连接位置对动态失速抑制有很大影响，整流段越长，抑制效果越好。

直升机旋翼； 动态失速； 分离涡； 主动流动控制； 充气前缘

与其他航空器相比，直升机具有垂直起降、空中悬停、低速机动等特殊能力，能够在复杂地形环境下执行任务，独特的飞行能力决定了其在军、民用领域中不可替代的作用。但在高速重载及机动飞行的情况下，直升机旋翼的后行桨叶会发生由大迎角引起的动态失速现象。动态失速的发生会导致桨毂和机身振动载荷激增，成为限制直升机飞行包线的重要因素之一，而翼型的动态失速特性基本决定了桨叶的动态失速特性。因此，如何减缓或抑制翼型动态失速的发生一直是直升机旋翼设计领域的研究热点和难点。

Chandrasekhara 等在1987—2004年间做了大量翼型动态失速的研究工作[1]。研究发现，在较高雷诺数下，导致翼型发生动态失速的原因是前缘附近的强逆压梯度和激波诱导分离[2]。因此，大部分针对动态失速控制的研究都集中于翼型前缘部分。目前，得到广泛研究的控制方法有前缘涡流发生器[3-5]、合成射流[6-10]、等离子体激励[11-14]、智能结构[15-16]等。此外，德国DLR宇航中心进行了一种用于旋翼的前缘动态下垂研究[17-18]，通过一种特殊设计的转动机构使得翼型前缘可以刚性旋转，在不同状态下对前缘进行变形，从而达到改变气动外形的目的。该装置有效改善了翼型的动态失速特性。虽然前缘动态下垂装置有很好的控制效果，但是装置复杂，很难在直升机旋翼的弹性桨叶上实际应用。文献[19]提出了一种比前缘动态下垂装置结构更简单的基于充气前缘(Inflatable Leading Edge，ILE)的流动控制方法，通过在NACA 63-212翼型前缘处安装一个可充放气的气囊来改变翼型前缘气动外形。从所给的结果来看，该方法能有效提高翼型的最大升力系数和失速迎角。文献[20]研究了ILE在定常来流下与流场的耦合作用对翼型气动特性的影响。数值研究表明，ILE增升效果明显，且在迎角较大时还具有较好的减阻效果，但ILE结构刚度会影响抑制静失速的效果。

文献[19-20]仅开展了ILE抑制静失速方面的工作，并未研究其对动态失速的控制能力。鉴于ILE方法在抑制静态失速方面的良好表现，为了拓展和深入对ILE方法的理解，有必要开展基于ILE方法的动态失速抑制研究。因此，本文将该方法应用到旋翼翼型的动态失速抑制中，重点研究和讨论以下几个方面：ILE抑制动态失速的控制机理；ILE最大膨胀状态的大小、对应迎角、保持时间对动态失速的影响；翼型上仰至不同迎角时开始充气对动态失速的影响；ILE整流单元与翼型连接位置对动态失速的影响。

1 充气前缘结构及外形计算方法

1.1 充气前缘结构

充气前缘是指在原翼型前缘处安装的一个由三段弹性结构组成的气囊，其剖面结构如图1所示，分为充气单元和整流单元两部分。充气单元由弹性结构BC、CC′组成，为密封设计，可以通过翼型表面的气孔进行充放气；整流单元由弹性结构AC、CC′组成，内部与大气相通，其不仅能改变充气单元的外形，还能起到整流的作用。ILE放气后在自身张力的作用下能紧贴壁面，因此可以保持原翼型的气动外形。由于AC段所用弹性结构的弹性模量远大于BC、CC′段的，所以本文假设AC段在充放气过程中不发生弹性变形。

在实际实施中，充放气孔设置在BC′段的翼型表面，输气管道经由翼型内部与外部的充放气设备相连，通过一个受控的往复运动活塞即可实现对充气气囊的外形控制。本文只针对二维的情况进行数值模拟研究，以验证该方案对动态失速进行控制的有效性。

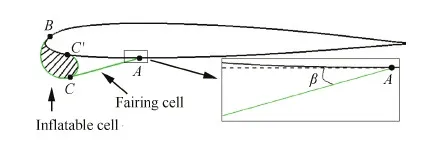
图1 充气前缘的结构Fig.1 Configuration of inflatable leading edge (ILE)

1.2 充气前缘外形计算方法

如图1中的局部放大部分所示，β为ILE整流段(线段AC)与翼型弦线的夹角，取逆时针为正。不同的β代表ILE的不同膨胀程度。计算中A、B、C′点在翼型上的横坐标分别为0.262 3c、0.014 1c、0.060 7c，c表示翼型弦长，文中如不加以说明则点A、B、C′均为上述位置。

根据文献[21]的实验参数，来流马赫数Ma=0.30，雷诺数Re=3.92×106，SC1095翼型的俯仰振荡规律为

α(t)=α0+αmsin(ωt)

(1)

式中：平均迎角α0=9.78°；迎角振幅αm=9.90°；减缩频率ω=0.099。

为了描述充气规律和翼型俯仰规律之间的联系，设函数γ(t)为

γ(t)=α0+αmsin(ωt+φ)

(2)

改变φ可以控制ILE最大膨胀状态对应不同迎角。ILE膨胀程度的描述参数β随γ(t)的变化规律为

(3)

若不加以说明文中均采用αmin=α1=-0.12°，α2=αmax=19.68°，βmin=-5°，βmax=15°，φ=0，a、b值由式(3)中其他参数联立计算得到。改变α1可以控制上仰至不同迎角时开始对ILE进行充气。改变α2可以控制ILE保持最大膨胀状态的持续时间。

在计算ILE外形时假设AC段不发生弹性形变，长度不变。在每个时间步上首先通过式(3)计算出β值，确定C点位置，然后通过求解出与线段AC相切且过B点或同时与翼型表面BC′相切的半径最大圆来确定ILE充气单元BC段的外形。本文计算中不考虑流场与ILE之间的流固耦合问题。

图2为充放气过程中的ILE外形变化图，给出了β分别为-4°、0°、5°、10°、15° 时的ILE外形。

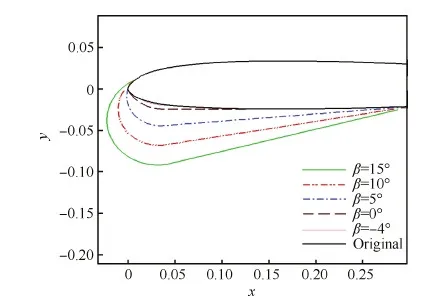
图2 充放气过程中的充气前缘外形Fig.2 Shapes of ILE in inflation process

2 数值计算方法及动网格实现步骤

基于自编的非结构混合网格流场解算程序，通过求解非定常Navier-Stokes方程对SC1095旋翼翼型的动态失速和基于ILE技术的SC1095旋翼翼型动态失速抑制进行数值模拟。对流项采用AUSM+-up格式进行空间离散，黏性通量采用Jameson二阶中心格式计算。为模拟旋翼翼型动态失速流场的非定常特性，采用双时间方法进行物理时间推进；伪时间推进采用LU-SGS隐式格式，可以有效增加时间步长，提高计算效率。湍流模拟采用Spalart-Allmaras一方程湍流模型做全湍流计算，并且求解过程与流动控制方程求解之间为松耦合。

图3 翼型计算网格Fig.3 Mesh for airfoil calculation

计算所用的三角形/四边形非结构混合网格如图3所示，分别为整个计算域网格、翼型周围网格、前缘处网格、后缘处网格。动网格的实现步骤为：首先，在每个时间步内计算出翼型的外形(包括ILE外形)；然后，采用网格点随体刚性运动方法实现四边形结构网格的变形；最后，通过弹簧光顺法对三角形非结构网格进行网格变形。

3 结果与讨论

3.1 数值方法和网格收敛性验证

为验证本文所用的数值计算方法对翼型动态失速特性的计算能力，对SC1095旋翼翼型的动态失速进行了数值模拟和验证。计算状态取自文献[21]的风洞试验，马赫数为0.30，雷诺数为3.92×106，俯仰运动的参数见式(1)。为准确模拟俯仰振荡过程中翼型的非定常气动力，将一个俯仰振荡周期等分为720个物理时间步，子迭代收敛标准为残值降至1×10-5。采用3套疏密不同的网格计算翼型的动态失速，以验证网格收敛性。3套计算网格单元数分别约为2.3万、7万和13万，翼型表面网格点依次加密，第1层网格高度均为翼型弦长的10-5。

图4给出了翼型升力、阻力和俯仰力矩系数CL、CD和Cm的计算值与实验值的对比情况。由图可以看出，计算值与实验值吻合较好，且3套不同疏密网格所计算出的升力、阻力和俯仰力矩系数之间相差很小。由此可见，本文所用数值计算方法可以有效计算出翼型动态失速过程中的气动力变化情况，并且中等规模网格足以保证计算精度。因此，在下文数值模拟计算中均采用中等规模的网格，并且在结果处理中原始翼型的结果均使用中等规模网格的计算值。

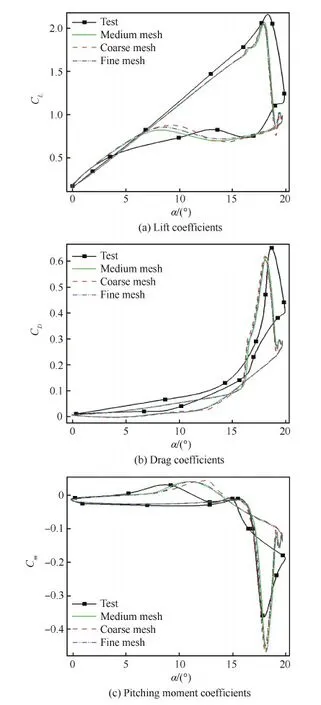
图4 气动系数计算结果与实验值的比较Fig.4 Aerodynamic coefficients comparison between calculation and test

3.2 ILE最大膨胀程度对翼型动态失速的影响

对不同最大膨胀程度的SC1095-ILE翼型(带ILE的SC1095翼型)动态失速进行数值模拟，以研究ILE最大膨胀程度βmax对翼型动态失速的影响。

从图5中的迟滞环可以看出βmax越大，ILE对动态失速的抑制效果越好，虽然最大升力系数略有降低，但是翼型的阻力系数和俯仰力矩系数峰值均大幅度下降。当βmax>19°后，ILE基本抑制了翼型的动态失速。再继续增大βmax时，ILE抑制翼型动态失速的能力仍有所增强。当βmax=25° 时，俯仰力矩系数峰值最小，ILE对动态失速的抑制效果最好。继续增加βmax时，俯仰力矩系数峰值略有增加，抑制效果减弱。

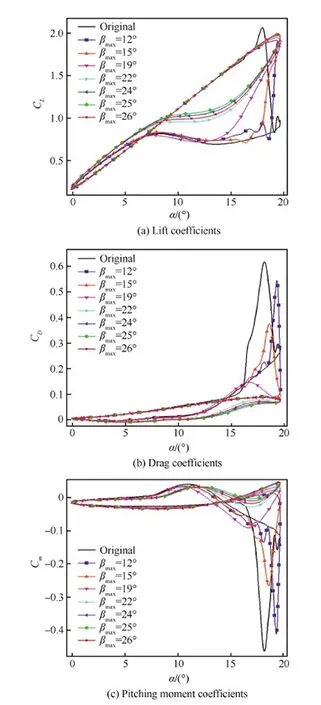
图5 ILE最大膨胀程度对气动系数的影响 Fig.5 Effect on aerodynamic coefficients of ILE maximum dilation

3.3 ILE抑制动态失速的控制机理分析

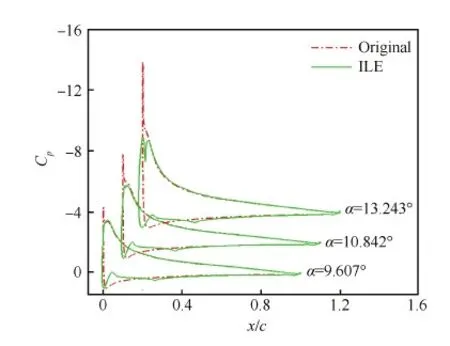
图6 压力系数分布对比Fig.6 Comparison of pressure coefficient distributions

本节以βmax=25° 为例，对比分析ILE对动态失速的控制机理。图6给出了3个迎角下的压力系数Cp对比图。迎角为9.607°时，两种翼型的流动均是附着状态，上翼面的逆压梯度均较小。上仰至10.842° 时，流动依然是附着状态，但是SC1095翼型的Cp峰值却显著增加，翼型上翼面处的逆压梯度增大，而SC1095-ILE翼型由于ILE的存在，其Cp峰值只是略有增加。翼型上仰到迎角为13.243°时，SC1095翼型的流动虽然还是附着状态，但Cp峰值已经增加到约-10；而此时SC1095-ILE翼型的流动也是附着状态，并且由于ILE的作用其Cp峰值未超过-5，逆压梯度更小。

图7和图8分别给出了SC1095翼型和SC1095-ILE翼型在上仰过程中迎角为14.372° 时的流场流线图及翼型表面压力系数曲线图，图中Original代表SC1095翼型，ILE代表SC1095-ILE翼型。图7中SC1095翼型上仰至14.372° 迎角时，由于在上翼面沿流向的逆压梯度过大导致在靠近前缘处出现前缘分离气泡，Cp峰值超过-11。从图8可以发现，SC1095-ILE翼型的Cp曲线出现2个峰值，这是由于ILE充分膨胀后，在ILE与翼型上翼面连接处B点位置形状不连续，形成了一个局部“凹坑”所致，图7(b)中右上角给出了该处局部放大的压力云图。

图9和图10给出了迎角为16° 时的流场和Cp对比情况。可见，SC1095翼型上仰至16° 的过程中，Cp峰值不断增长，并超过-12，不断增大的逆压梯度导致前缘分离气泡不断变大并开始向后缘发展；而由于ILE的作用，SC1095-ILE翼型上没有产生前缘分离涡。

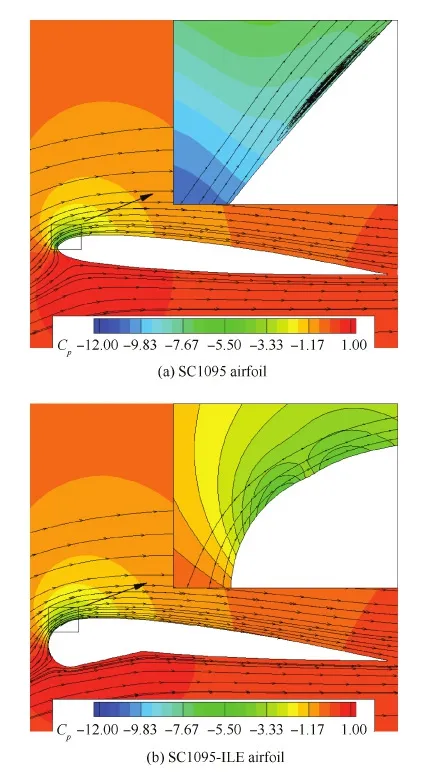
图7 迎角为14.372° 时的翼型流场Fig.7 Flow fields of airfoils at α=14.372°

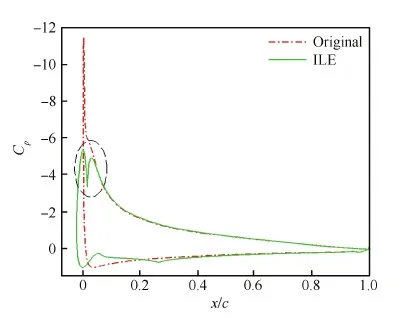
图8 迎角为14.372° 时翼型表面压力系数对比(Ma=0.30, Re=3.92×106)Fig.8 Comparison of airfoil surface pressure coefficient distributions at α=14.372° (Ma=0.30, Re=3.92×106)

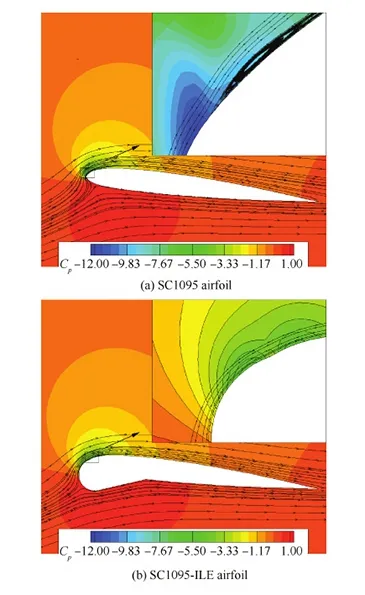
图9 迎角为16° 时的翼型流场Fig.9 Flow fields of airfoils at α=16°

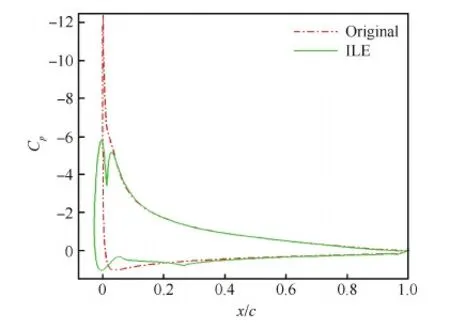
图10 迎角为16° 时翼型表面压力系数对比(Ma=0.30, Re=3.92×106)Fig.10 Comparison of airfoil surface pressure coefficient distributions at α=16° (Ma=0.30, Re=3.92×106)

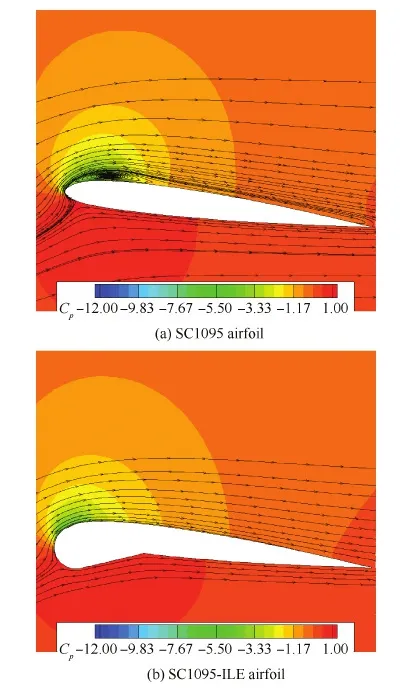
图11 迎角为16.398° 时的翼型流场Fig.11 Flow fields of airfoils at α=16.398°

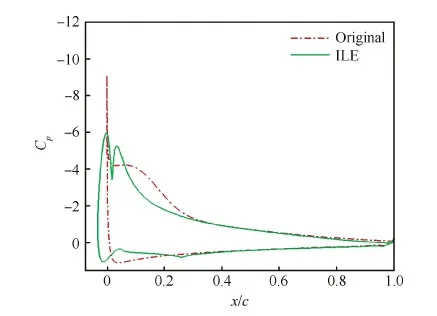
图12 迎角为16.398° 时翼型表面压力系数对比(Ma=0.30, Re=3.92×106) Fig.12 Comparison of airfoil surface pressure coefficient distributions at α=16.398°(Ma=0.30, Re=3.92×106)

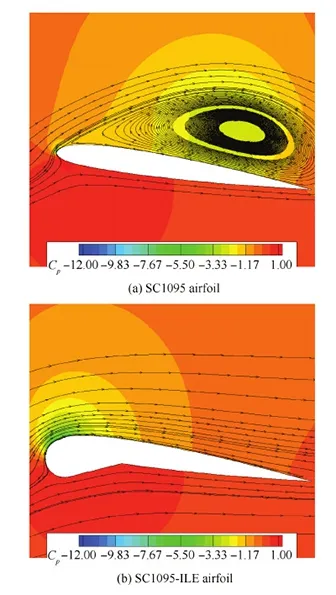
图13 迎角为18.014° 时的翼型流场Fig.13 Flow fields of airfoils at α=18.014°

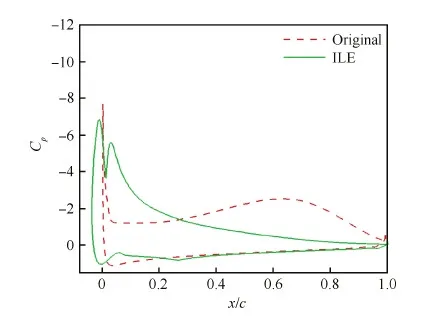
图14 迎角为18.014° 时翼型表面压力系数对比(Ma=0.30, Re=3.92×106) Fig.14 Comparison of airfoil surface pressure coefficient distributions at α=18.014°(Ma=0.30, Re=3.92×106)

图11～图14给出了迎角为16.398° 和18.014° 时的流场和Cp对比情况。SC1095翼型在上仰至16.398° 迎角时，前缘分离气泡已经向后缘移动一段距离，并且发展成了一个较大的分离涡，在该分离涡向后缘移动的过程中Cp峰值不断下降，但由于该分离涡形成的低压效应，翼型升力系数依然逐渐变大，阻力系数和力矩系数也不断增大。SC1095翼型继续上仰至18.014° 迎角的过程中，分离涡继续不断变大并向后缘移动，翼型的升、阻力系数和俯仰力矩系数继续增长，当达到18.014° 迎角时SC1095翼型的升力系数接近最大值。对于SC1095-ILE翼型，在上仰至18.014° 迎角的过程中，ILE外形不断变大，持续改变着SC1095-ILE翼型的前缘变径，Cp峰值变化平缓，减缓了逆压梯度的增长，进而有效地抑制了翼型前缘分离涡的产生和发展，阻止了动态失速的发生，大大降低了翼型的阻力系数和俯仰力矩系数的峰值。

图15和图16分别给出了SC1095翼型和SC1095-ILE翼型在上仰至最大迎角19.680° 时的流场流线图及翼型表面Cp曲线图。由迎角18.014° 持续上仰至最大迎角19.680° 的过程中，SC1095翼型已经完全失速，升力系数骤降，并在上翼面区域产生大范围的分离涡。由于ILE在之前的翼型上仰运动中抑制了前缘分离涡的产生，所以在由迎角18.014° 上仰至最大迎角19.680° 的过程中，SC1095-ILE翼型依然保持了很好的附着流动，只是在翼型后缘处出现小范围的分离流动，没有发生失速。在达到最大迎角19.680° 后，翼型开始下俯。SC1095翼型在下俯过程中发生涡的移动和脱落，Cp峰值不断下降，阻力系数和俯仰力矩系数不断减小。SC1095-ILE翼型在下俯过程中后缘处也出现较大分离，并伴随有涡的脱落，其Cp峰值不断下降，升力系数不断减小。当SC1095翼型下俯至约7° 迎角、SC1095-ILE翼型下俯至约9° 迎角时，流动重新恢复到附着状态。

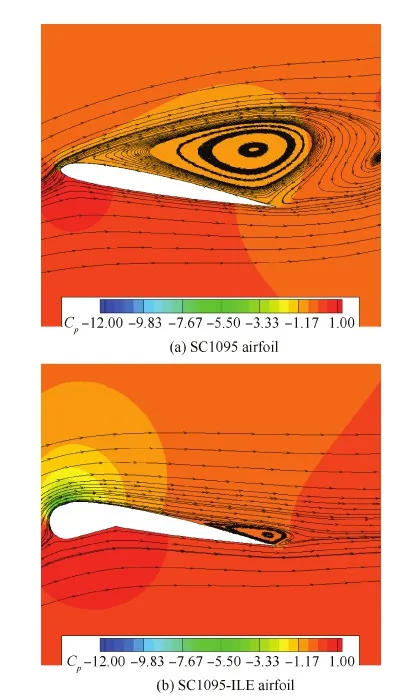
图15 迎角为19.680° 时的翼型流场Fig.15 Flow fields of airfoils at α=19.680°

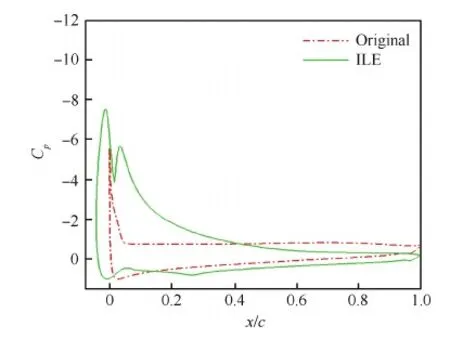
图16 迎角为19.680° 时翼型表面压力系数对比(Ma=0.30, Re=3.92×106) Fig.16 Comparison of airfoil surface pressure coefficient distributions at α=19.680°(Ma=0.30, Re=3.92×106)

可见，ILE可以阻止前缘分离涡的产生和发展，从而能够有效抑制翼型动态失速的发生。从图5(a)可以看出，SC1095-ILE翼型的升力系数迟滞环面积已经大为减小。

3.4 ILE最大膨胀状态对应不同迎角对动态失速的影响

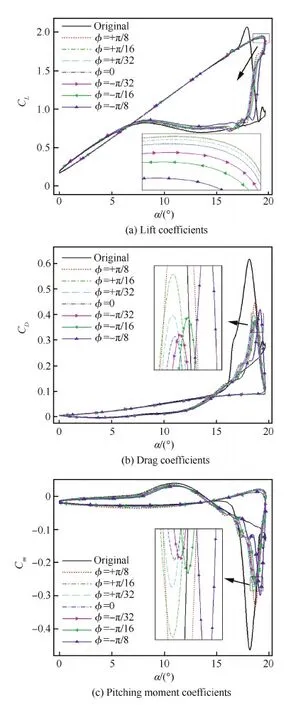
图17 ILE最大膨胀状态对应迎角的影响Fig.17 Effect of angles of attack at which ILE reaches maximum dilation

图17给出了ILE最大膨胀状态对应不同迎角时的翼型气动力曲线。图中φ=+π/8、φ=+π/16、φ=+π/32分别表示翼型上仰至迎角为15.89°、17.75°、18.71°时ILE刚好膨胀到最大，翼型继续上仰时ILE开始放气，变小；φ=0表示翼型上仰时ILE充气，当翼型达到最大迎角时ILE刚好膨胀到最大，翼型下俯时ILE放气；φ=-π/32、φ=-π/16、φ=-π/8分别表示翼型下俯至迎角为18.71°、17.75°、15.89°时ILE刚好膨胀到最大，翼型继续下俯时，ILE开始放气，变小。计算中βmax为15°。

总体来说，ILE达到最大膨胀程度时所对应的迎角状态对于动态失速抑制效果的影响不大。当φ>0时，翼型最大升力系数略有增加，而φ<0时则有所减小。在φ≠0时，翼型的阻力系数、俯仰力矩系数的峰值均略有增加，且φ的绝对值越大则阻力系数和俯仰力矩系数的峰值增加越多。可见，从降低阻力和力矩系数峰值的角度来看，φ=0即在上仰至最大迎角时ILE达到最大膨胀程度，控制效果最好。

3.5 ILE保持最大膨胀状态的时间对动态失速的影响

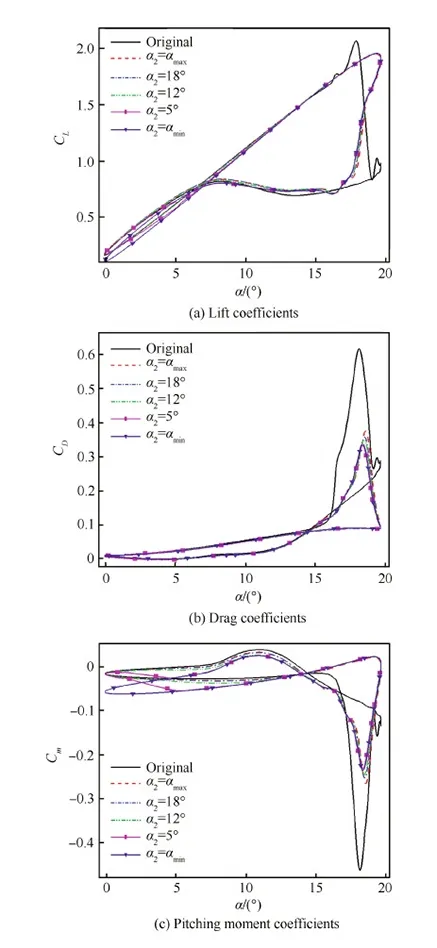
图18 ILE最大膨胀程度保持时间的影响Fig.18 Effect of duration of ILE maximum dilation

如图18所示，为研究ILE保持最大膨胀状态的时间(即当翼型大于某一迎角后ILE始终保持最大膨胀状态)对动态失速抑制的影响规律，选择5个工况进行计算，分别为α2=αmin、5°、12°、18°、αmax。其中，α2=18° 表示当翼型迎角大于18° 后ILE始终保持最大膨胀状态，其他以此类推。可见，ILE保持最大膨胀状态的时间长短对动态失速抑制效果的影响不大，较长的保持时间可以略微降低阻力系数和俯仰力矩系数的峰值。但是，过长时间保持最大膨胀状态(例如α2=αmin表示一直保持最大膨胀状态)会在小迎角时产生较大的低头力矩。因此，为了简化对ILE的控制过程，应尽量缩短ILE保持最大膨胀状态的时间。

3.6 翼型上仰至不同迎角时开始充气对动态失速的影响

选择了6个工况进行计算，分别为α1=αmin、5°、10°、12°、13°、15°，以研究在翼型上仰至不同迎角时开始充气对翼型动态失速抑制效果的影响规律。其中，α1=5° 表示翼型上仰至迎角为5° 时对ILE开始充气，上仰至最大迎角时ILE刚好膨胀到最大，翼型下俯至迎角为5° 时ILE放完气体，并在自身张力作用下紧贴在原翼型上，其他以此类推。

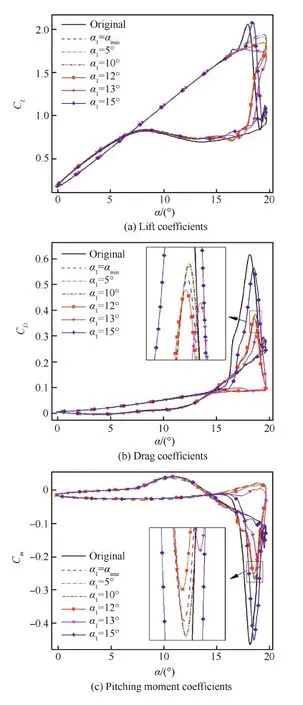
图19 ILE开始充气时迎角位置的影响 Fig.19 Effect of angles of attack at which ILE is started to be dilated

如图19所示，在α1不断增大至10° 的过程中，翼型的最大升力系数略有降低，当α1大于10° 后最大升力系数降低幅度变大，继续增加α1至15° 时最大升力系数又突然增大，略微超过原翼型，且增大了升力系数迟滞环面积。对于阻力特性，α1增加时阻力的最大值略有增加，当α1=12°、13° 时阻力峰值均下降，达到15°时则又突然急剧变大，仅比原翼型值略低。对于力矩特性，与阻力特性的变化规律一致，力矩的峰值先是随α1的值增大而变大，之后减小，当α1=15° 时又突然变大，仅略小于原翼型值。α1=15° 意味着在翼型产生前缘分离涡之后才开始对ILE进行充气，虽然ILE快速膨胀，但已无法有效抑制分离涡的增长和向后缘移动，最终导致SC1095-ILE翼型较早发生失速，ILE抑制动态失速的作用大为减弱。而α1=αmin则表示翼型开始上仰就对ILE进行充气，在产生前缘分离涡之前ILE已经达到一定膨胀程度，很好地降低了Cp的峰值，减缓了流动的逆压梯度，阻止了前缘分离涡的产生，进而抑制了SC1095-ILE翼型动态失速的发生。

3.7 ILE整流单元与翼型连接位置对动态失速的影响

通过改变ILE整流单元与翼型连接位置(A点的位置)来研究A点位置对翼型动态失速的影响。计算中B、C′点均保持原来位置不变，x为A点在翼型上相对于翼型前缘的横坐标位置。计算结果如图20所示。可见，A点越靠近前缘(即整流段越短)，其对动态失速的抑制作用越弱。当x=0.08c、0.12c时，虽然延迟了失速发生的迎角，但是产生了更大的升、阻力和力矩系数峰值，且显著增大了升力系数迟滞环面积。A点越靠后，整流段越长，则ILE对动态失速的抑制效果越好。当x=0.08c时，由于整流段较短，SC1095-ILE翼型的前缘半径小，在上翼面沿流向的逆压梯度较大而导致在靠近前缘处出现分离涡，且不断变大并向后缘移动，最终导致SC1095-ILE翼型失速。而当x=0.30c时，在上仰过程中，由于ILE的整流段更长，翼型前缘半径更大，可以降低Cp峰值，减小流动的逆压梯度，进而有效地抑制流动的分离，阻止动态失速的发生，大大降低了翼型的阻力系数和俯仰力矩系数的峰值。

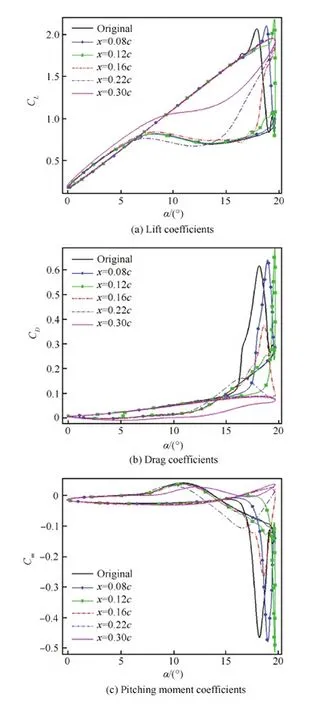
图20 ILE整流单元与翼型连接位置的影响 Fig.20 Effect of connection locations of ILE rectifier unit and airfoil

4 结 论

1) 通过阻止前缘分离涡的产生和发展，ILE能够有效地抑制动态失速的发生，可以在最大升力系数下降不大的情况下，非常显著地降低阻力和俯仰力矩系数的峰值，明显改善了翼型的动态失速特性。

2) 在点A、B、C′位置不变的情况下，ILE最大膨胀程度越大，即βmax越大，其抑制动态失速的效果越好。在本文选取的翼型和计算参数条件下，最大膨胀程度βmax=25° 时具有最佳控制效果。当βmax>25° 时，其对动态失速的抑制效果开始减弱。

3) 翼型上仰至最大迎角且ILE刚好达到最大膨胀状态时，其对动态失速的抑制效果更好。

4) ILE保持最大膨胀状态的时间长短对动态失速抑制效果影响不大。

5) 在翼型上仰至不同迎角时开始对ILE充气会对动态失速抑制有较大影响。在翼型上仰至较大迎角才开始充气会减弱对动态失速的抑制作用，在本文选取的翼型和计算参数条件下，当翼型上仰至迎角为15°后开始充气会失去对动态失速的抑制作用。

6) ILE整流段与翼型连接位置对动态失速抑制有很大影响，整流段越长对动态失速的抑制效果越好。

在实际的直升机旋翼前飞过程中，翼型的实际迎角与桨叶的变距、挥舞、方位角以及当地诱导下洗速度等因素密切相关，而且存在旋转三维效应，这些复杂因素会对实际的控制效果产生一定影响。根据本文的研究结论，通过合理地设计ILE装置并设置充放气参数，可以尽可能降低这种影响。本文只是针对SC1095翼型这一种旋翼翼型得出上述研究结论，而且只计算了一个特定的俯仰状态，但从结论可以看出充气前缘技术具有很好的控制效果和应用前景，文中的研究方法和思路也可以进一步应用于其他翼型和工况。此外，本文的充气前缘技术在动态入流情况下以及三维情况下的控制效果和控制机理有待进一步的研究。

[1] EKATERINARIS J A, CHANDRASEKHARA M S, PLATZER M F. Recent development in dynamic stall measurements, computations and control: AIAA-2005-1296[R]. Reston: AIAA, 2005.

[2] CHANDRASEKHARA M S, WILDER M C, CARR L W. Compressible dynamic stall control: A comparison of different approaches: AIAA-1999-3122[R]. Reston: AIAA, 1999.

[3] MARTIN P, WILSON J, BERRY J, et al. Passive control of compressible dynamic stall: AIAA-2008-7506[R]. Reston: AIAA, 2008.

[4] MAI H, DIETZ G, GEISSLER W, et al. Dynamic stall control by leading-edge vortex generators[J]. Journal of the American Helicopter Society, 2008, 53(1): 26-36.

[5] PAPE A L, COSTES M, RICHEZ F, et al. Dynamic stall control using deployable leading-edge vortex generators[J]. AIAA Journal, 2012, 50(10): 2135-2145.

[6] RAJU R, MITTAL R, CATTAFESTA L. Dynamics of airfoil separation control using zero-net mass-flux forcing[J]. AIAA Journal, 2008, 46(12): 3103-3115.

[7] DENG X, XIA Z X, LUO Z B, et al. Vector-adjusting characteristic of dual-synthetic-jet actuator[J]. AIAA Journal, 2015, 53(3): 794-797.

[8] 罗振兵, 夏智勋. 合成射流技术及其在流动控制中应用的进展[J]. 力学进展， 2005, 35(2): 221-234.

LUO Z B, XIA Z X. Advances in synthetic jet technology and applications in flow control[J]. Advances in Mechanics, 2005, 35(2): 221-234 (in Chinese).

[9] ZHAO G Q, ZHAO Q J. Parametric analyses for synthetic jet control on separation and stall over rotor airfoil[J]. Chinese Journal of Aeronautics, 2014, 27(5): 1051-1061.

[10] ZHAO G Q, ZHAO Q J, GU Y S, et al. Experimental investigations for parametric effects of dual synthetic jets on delaying stall of a thick airfoil[J]. Chinese Journal of Aeronautics, 2016, 29(2): 346-357.

[11] POST M L, CORKE T C. Separation control using plasmas actuators-stationary and oscillating airfoils: AIAA-2004-0841[R]. Reston: AIAA, 2004.

[12] CORKE T C, POST M L. Overview of plasma flow control concepts, optimization, and applications: AIAA-2005-0563[R]. Reston: AIAA, 2005.

[13] POST M L, CORKE T C. Separation control using plasma actuators: Dynamic stall vortex control on oscillating airfoil[J]. AIAA Journal, 2006, 44(12): 3125-3135.

[14] 李应红, 吴云, 梁华, 等. 提高抑制流动分离能力的等离子体冲击流动控制原理[J]. 科学通报，2010, 55(31): 3060-3068.

LI Y H， WU Y， LIANG H, et al. The mechanism of plasma shock flow control for enhancing flow separation control capability[J]. Chinese Science Bulletin, 2010, 55(31): 3060-3068 (in Chinese).

[15] BARLAS T K, VAN KUIK G A M. Review of state of the art in smart rotor control research for wind turbines[J]. Progress in Aerospace Sciences, 2010, 46(1): 1-27.

[16] STRAUB F K. A feasibility study of using smart materials for rotor control[J]. Smart Materials and Structures, 1996, 5(1): 1-10.

[17] GEISSLER W, DIETZ G, MAI H, et al. Dynamic stall control investigation on a full size chord blade section[C]//30th European Rotorcraft Forum. Cologne: German Aerospace Center (DLR), 2004.

[18] GEISSLER W, DIETZ G, MAI H. Dynamic stall on a supercritical airfoil[C]//29th European Rotorcraft Forum. Cologne: German Aerospace Center (DLR), 2003.

[19] WERNICKE K G, WERNICKE R K. Inflatable wing leading edges for high life and deicing: NASA Tech Briefs[R]. Washington, D.C.: NASA, 2000.

[20] 蒋跃文, 叶正寅, 张正科. 充气结构与流场的耦合求解方法[J]. 力学学报， 2010, 42(1): 1-7.

JIANG Y W, YE Z Y, ZHANG Z K. Model of inflatable structure/fluid interaction for variable leading edge[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(1): 1-7 (in Chinese).

[21] MCALISTER K W, PUCCI S L, MCCROSKEY W J, et al. Experimental study of dynamic stall on advanced airfoil section: NASA-TM-84245-VOL-2[R]. Washington, D.C.: NASA Ames Research Center, 1982.

(责任编辑： 李明敏)

Dynamic stall suppression for rotor airfoil based on inflatable leading edge technology

XUHeyong1,*，XINGShilong1,YEZhengyin1,MAMingsheng1,2

1.NationalKeyLaboratoryofScienceandTechnologyonAerodynamicDesignandResearch,NorthwesternPolytechnicalUniversity,Xi’an710072,China2.ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China

The occurrence of dynamic stall will result in high vibration torque loads and limit the flight envelope of a helicopter at high speed and load. Through the method of computational fluid dynamics (CFD)， dynamic stall suppression for SC1095 helicopter rotor airfoil based on inflatable leading edge (ILE) technology is studied. The control mechanism of dynamic stall suppression and the effect of structure and inflating process of ILE are analyzed. The result shows that the dynamic stall suppression method based on ILE is effective. The bigger the expansion of the ILE，the better the effect of the ILE on dynamic stall suppression. However, if the ILE is too great, the effect will become weak. If the expansion of the ILE reaches the maximum when the airfoil pitches to the maximum angle of attack，the best control performance can be achieved. The duration of the maximum expansion state of the ILE has minor effect on the control performance. The angle of attack at which the ILE starts to swell has a great effect on the control ability. The position which connects the ILE and the airfoil has a great effect on dynamic stall suppression. A longer fairing section of the ILE has a better effect on dynamic stall suppression.

helicopter rotor; dynamic stall; separation vortex; active flow control; inflatable leading edge

2016-09-14；Revised2016-10-11；Accepted2016-11-22；Publishedonline2016-11-241034

URL：www.cnki.net/kcms/detail/11.1929.V.20161124.1034.004.html

s：NationalNaturalScienceFoundationofChina(11472223，11202166)

2016-09-14；退修日期2016-10-11；录用日期2016-11-22； < class="emphasis_bold">网络出版时间

时间：2016-11-241034

www.cnki.net/kcms/detail/11.1929.V.20161124.1034.004.html

国家自然科学基金 (11472223，11202166)

*

.E-mailxuheyong@nwpu.edu.cn

许和勇， 邢世龙， 叶正寅， 等． 基于充气前缘技术的旋翼翼型动态失速抑制J． 航空学报,2017,38(6):120799.XUHY,XINGSL,YEZY,etal.DynamicstallsuppressionforrotorairfoilbasedoninflatableleadingedgetechnologyJ.ActaAeronauticaetAstronauticaSinica,2017,38(6):120799.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0308

V211.3； V211.52

A

1000-6893(2017)06-120799-13

*Correspondingauthor.E-mailxuheyong@nwpu.edu.cn