双后掠乘波体设计及性能优势分析
2017-11-22刘传振白鹏陈冰雁
刘传振, 白鹏, 陈冰雁
中国航天空气动力技术研究院, 北京 100074
双后掠乘波体设计及性能优势分析
刘传振, 白鹏*, 陈冰雁
中国航天空气动力技术研究院, 北京 100074
根据密切锥乘波体的设计几何关系,提出双后掠乘波体概念,给出了双后掠乘波体设计的参数与生成乘波体外形之间的关系。使用非均匀有理B样条(NURBS)表达包括圆和直线的激波出口型线辅助设计,研究了钝头区域可控、后掠区域可控的乘波体外形设计方法。使用CFD数值计算方法验证了设计方法的有效性,同时研究了双后掠乘波体外形的性能优势,结果表明在保持高超声速高性能的基础上适当设计外形在低速状态、纵向稳定性和涡效应增升方面具有性能优势,为大空域宽速域高超声速飞行器的研制开拓了新的途径。
乘波体; 双后掠; 低速性能; 稳定性; 涡升力
高升力超声速/高超声速外形一直是人类不懈的追求。根据高超声速无黏流动的双曲型特征,飞行器的气动性能可以在很大程度上得以提高,乘波体就是利用这一特性的典型外形。乘波体通过附着激波将高压气流限制在飞行器下表面阻止流动泄露,有效突破了高超声速飞行器的升阻屏障,具有很高的升阻比。经过几十年的发展,乘波体从早期的单一构型逐渐发展为具有不同特点的复杂构型。Nonweiler首先提出了楔形流场乘波体[1],Jones等使用锥形流场进行设计,有效提高了乘波体的容积率[2],后续有些学者发展了其他的基准流场,从带迎角锥、椭圆锥流动[3-4]等到一般三维流动[5-6]都有涉及,大大拓展了设计空间,而密切锥方法[7]的提出更是提高了灵活性,可以得到具有特殊性质的乘波体外形[8-9]。
乘波体的工程应用目前仍然有诸多限制,主要问题有3点:容积率不高,低速状态气动性能不好,纵向稳定性难以保证。目前有一些解决方法,例如容积率可以通过修改上表面外形进行扩充[10],低速状态则可以通过串联不同设计状态的乘波体提高[11],纵向稳定性则可以通过改变基准流场部分改善[12]。这些方法具有较好的工程应用价值,但大部分手段灵活性和可控性不好,难以提取设计参数进行控制。乘波体外形一般根据高超声速流场通过流线追踪得到,其生成曲面具有独特的特征,难以自由设计,但乘波体的平面形状可以通过设计曲线进行修改,这为改善乘波体在非设计点的气动性能提供了一种非常值得考虑的思路,而定后掠角乘波体的概念则为这一思路提供了有效途径。
定后掠角乘波体由来已久。Starkey和Lewis[13]提出了一种定常楔形角乘波体方法,Jones介绍了一种设计曲线过圆锥顶点的定后掠乘波体,但这些设计方法有的不够灵活,有的设计空间受限,应用较少。最近几年,洛克希德·马丁公司的Rodi[14-15]从密切锥乘波体设计方法出发,提出了定后掠角密切锥和密切流场乘波体的概念,介绍了这类乘波体潜在的性能优势;段焰辉等[16]则给出了定后掠角乘波体具体的设计方法,提取设计变量进行了分析研究。通过这些工作设计得到了给定前缘的三角翼乘波体,为通过定制平面形状改善乘波体的气动性能奠定了基础。
本文延伸了定后掠乘波体概念,通过对设计曲线的修改提出了双后掠乘波体的概念,大大提高了密切锥方法的灵活性,同时使用非均匀有理B样条(Non-Uniform Rational B-Spline, NURBS)表达设计曲线进行辅助设计,增强了设计方法的可控性,并保证了乘波体曲面的连续光滑。双后掠乘波体外形兼顾了不同速域性能的气动优势,本文使用计算流体力学(Computational Fluid Dynamics, CFD)方法对其亚声速状态、纵向稳定性以及涡升力非线性增加等性能优势进行了探索,得到了有价值的结论。
1 设计方法
1.1 双后掠乘波体设计
密切锥乘波体设计方法是一种反设计方法,由给定的激波形状拟合流场并生成乘波体。需要给出的设计曲线包括激波出口型线——也叫做进气捕获曲线(Inlet Capture Curve, ICC)和流线追踪的初始线——捕获流管(Flow Capture Tube, FCT)。密切锥乘波体设计中,ICC曲线和FCT曲线的形状直接决定了乘波体的外形。本节讨论2个有用的几何关系式,确定设计参数与乘波体外形之间的关系,然后给出了双后掠乘波体的设计方法。

图1 密切锥乘波体后掠角关系图Fig.1 View of sweep angle relationships of osculating cone waverider
图1给出了密切锥乘波体设计方法的局部示意图,首先作ICC曲线在G点的切线,过此点的垂面GH即为密切平面,密切平面内使用锥形流拟合,流场一般采用数值方法求解Taylor-Macoll方程得到,尺度由ICC曲线的当地曲率半径决定,如果ICC当地为直线,则曲率半径无穷大,可使用二维楔形流动代替。H点为密切平面与FCT曲线的交点,在H点作FCT的当地切线。ICC在G点斜率倾角为δ,FCT在H点处的斜率倾角为δ1,对应乘波体部分的长度为l、宽度为s,λ为前缘后掠角。那么有

(1)
式中:β为有效激波角。当δ1=δ时,即有文献[14]中提到的关系式:
sinδ=tanλtanβ
(2)
在密切锥乘波体设计中,此条件为全域性(Universally),即使ICC和FCT曲线不为直线,此条件也成立。因为流场和激波的影响对乘波体性能更具决定性,在应用这一关系式时,一般将FCT设定为水平直线而修改ICC曲线的形状。
第2个关系是下表面偏转角关系,即

(3)
式中:ε为ICC曲线与乘波体下表面型线之间的夹角;γc为锥形流中的半锥角。已知ε和δ可以确定下表面的厚度分布。这是一个比较弱的条件,依赖于密切平面使用锥形流作为流场,此时流线的方向平行于圆锥的母线方向。
文献[14]使用式(2)和式(3)给出了定后掠乘波体的概念,生成得到了三角翼布局乘波体。本文拓展这一方法,如图2所示,给出了双后掠角乘波体的设计方法。指定FCT为直线,ICC由一段直线和圆弧组成,直线段与圆弧不相切,一般取直线段倾角小于圆弧圆心角,否则会导致乘波体下表面产生重叠。r为FCT偏移圆弧圆心的距离,当r为0时,设计得到的是尖头乘波体,当r>0时,设计得到的是钝头乘波体。圆弧与直线的交接点B处容易产生乘波体下曲面不连续的情况,本文通过设定此点附近区域的斜率和曲率由圆弧到直线部分逐渐过渡予以缓解,所生成乘波体的平面形状如图2所示,图中,A、B、C、D、I、Q、Q1、Q2、S、P、T1、T2均为几何点。
图2所示的设计参数与乘波体外形的控制参数之间存在对应的几何关系,假设O点为坐标原点,圆弧半径为R,FCT偏移距离为r,圆弧圆心角为θ1,直线段倾角为θ2。乘波体长度为
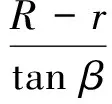
(4)
乘波体宽度为

(5)
钝头区域宽度为
sd=Rsinθ1-tanθ1(Rcosθ1-r)
(6)
当r=0时,所生成的外形为尖头乘波体,当r=Rcosθ1时,此设计方法方法退化为FCT为水平直线的锥导乘波体,有时r取值不够直观,本文使用钝头度ζ=r/(Rcosθ1)将其归一化;第一后掠区域宽度为
s1=(Rcosθ1-r)(tanθ1-tanθ2)
(7)
第二后掠区域宽度为

(8)

图2 双后掠乘波体设计Fig.2 Double swept waverider design
第一后掠区域前缘线不是严格意义的直线,可以近似取T1、T2两点的斜率角作为第一后掠角λ1,即
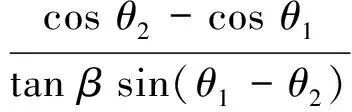
(9)
第二后掠角λ2可根据式(2)计算:

(10)
同时第二后掠部分的厚度分布可以根据式(3)求解:
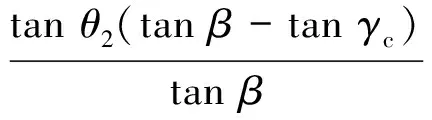
(11)
根据式(6)、式(9)~式(11),可以通过钝头区域、后掠角大小和厚度分布求解r、β、θ1、θ2,因此此方法具有给定乘波体的平面形状生成乘波体外形的能力。
1.2 使用NURBS辅助设计
双后掠乘波体设计方法扩大了乘波体的设计空间,具有良好的灵活性。但图2所示方法生成的外形,其后掠区域的大小难以控制;过渡点处斜率变化剧烈,难以保证乘波体下表面在相应位置的光滑连续性。
为了解决这个问题,本文引入非均匀有理B样条方法表达ICC曲线进行设计。NURBS已经成为利用计算机处理几何信息时用于形状表示、设计和数据交换的工业标准,受到了人们的广泛关注。分析图2中ICC曲线的构成,主要包括圆弧和直线部分。NURBS方法的一个最大优点就是能够精确表示包括圆在内的圆锥截线[17],这一特性在进行密切锥设计时具有很大的便利。
p次NURBS曲线的定义为

(12)
式中:Pi为控制点;wi为权因子;Ni,p(u)为定义在非周期非均匀节点矢量上的p次B样条基函数。
NURBS方法可以通过特定的控制点生成圆弧,也可以给定半径和圆心角生成一段圆弧。直线的表达则可以通过共线的p+1个点生成。
图3给出了使用二次NURBS表达包括圆和直线在内的曲线辅助乘波体设计的示意图,为了控制第一后掠区域的范围,本文增加过渡段,同时使用重节点技术控制曲线保证圆和直线互不干扰。具体实施如下:A、E、B、F、C、D点为NURBS生成ICC曲线的控制点,其中A、E、B点确定圆弧部分,圆心角为θ1,F、C、D点共线,产生斜率倾角为θ2的直线,B、F、C点控制圆弧与直线的过渡段。F点的位置很重要,它控制第一后掠区域的大小,也影响乘波体的总宽度,F点的选取方法如下:沿圆弧在B点的切线向上延伸至FCT曲线,给定控制参数0≤ω≤1,在切线段上选择F点的位置,当ω=0时,F点与B点重合,方法退化为图2 所示的双后掠乘波体设计,当ω=1时,F点到达FCT曲线,方法退化为三角翼乘波体设计。
增加了控制参数ω之后,乘波体的平面控制参数如下:
1) 乘波体长度为
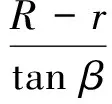
(13)
2) 乘波体宽度为
(14)
3) 钝头区域大小为
sd=Rsinθ1-tanθ1(Rcosθ1-r)
(15)
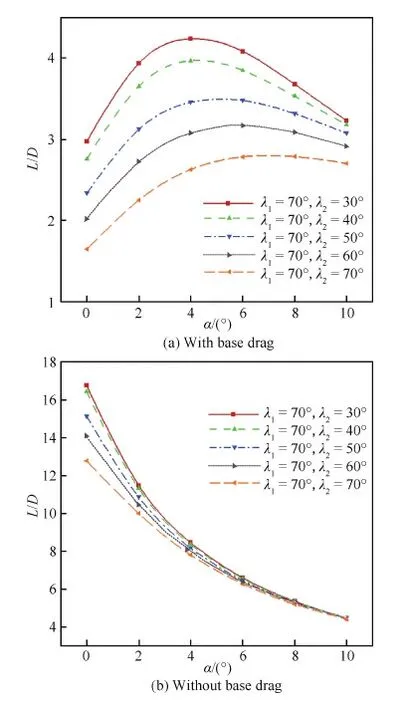
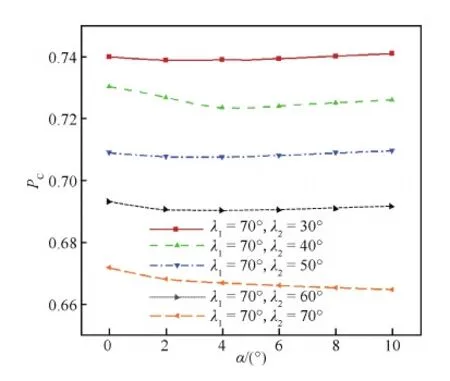
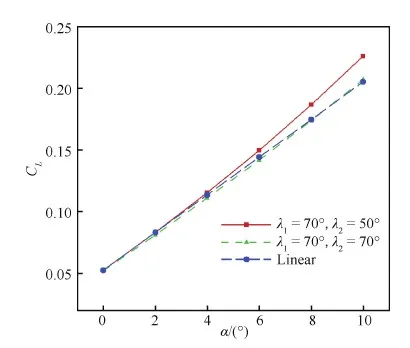
NURBS曲线的节点矢量为[0 0 0a1a1a21 1 1],0 图3 使用NURBS的双后掠乘波体设计方法Fig.3 Double swept waverider design method aided with NURBS 图4 设计曲线及其对应的乘波体Fig.4 Waveriders corresponding to different design curves 使用NURBS表达ICC曲线,保证了第一后掠段斜率和曲率的光滑过渡,使乘波体平面形状和表面曲面的过渡更加光顺,同时增加参数ω,后掠段的区域大小也可以控制。图4给出了改变NURBS控制点所得到的ICC曲线及其所对应的乘波体外形,本方法可以生成尖头双后掠乘波体外形和钝头乘波体外形,同时可以改变后掠区域和角度,指定平面形状设计外形。 1.3 设计变量提取和性能快速预估 从设计方法中本文得到双后掠乘波体的设计参数包括圆弧半径R、钝头区域控制参数r、激波角β、ICC曲线的偏转角θ1和θ2以及第一后掠区域控制量ω。根据方法部分的分析,通过这些控制参数可以控制乘波体的长度l、宽度s、钝头区域大小sd、第一和第二后掠区域s1和s2、第一和第二后掠角大小λ1和λ2以及下表面厚度分布ε等平面控制参数。相应的,也可以通过这些平面控制参数反推得到设计参数,因此设计变量可以选取平面控制参数。为了简单直观,在下文的性能分析中选定的设计变量为R、r、β、λ1、λ2、ω等。选定这些参数后,即可通过定制平面形状生成乘波体外形。 使用密切锥进行乘波体设计时,所生成的外形中存储有无黏流场信息,可以通过流线积分法评估无黏气动力。高超声速条件下,黏性在阻力中占有很大的比重,因此在乘波体设计中需要把黏性效应考虑进去。本文使用基于流线的黏性力计算方法[18]进行预估。除了气动特性,飞行器的容积也是一个非常重要的参考量,一般定义容积率作为容积的参考量,τ=V2/3/S,V为容积,S为平面投影面积。 双后掠乘波体的核心价值在于保持高超声速高性能的基础上,提高非设计点状态的气动性能,改善传统乘波体的缺陷,因此具有重要的探索意义和实用价值。本文的研究表明,适当设计的双后掠乘波体在保持高超声速特性的基础上具有低速性能好、纵向稳定性强等优点,同时随迎角增加部分外形也具有升力的非线性增加特性。 2.1 设计方法CFD验证 流线积分法和基于流线的黏性力计算方法可以方便地估计乘波体的气动性能,效率很高,但精度不能保证,也无法计算非设计点状态的气动性能。本节使用中国航天空气动力技术研究院自主研发、具有完全知识产权的CFD数值模拟软件平台——GiAT进行数值验证计算,计算网格为非结构网格,湍流模型使用Spalart-Allmaras模型。 在不同的设计状态下选择尖头和钝头2个外形对乘波体设计和性能快速预估方法进行CFD验证,设计状态和设计变量如表1所示。 表2给出了尖头外形CFD方法和乘波体快速预估(WR)方法得到的气动力对比,其中CL、CDinv、CDvis、CD分别为升力系数、无黏阻力系数、有黏阻力系数、总阻力系数,升阻比L/D的误差为4.7%,计算结果吻合较好。 图5给出了尖头乘波体下表面等压线,激波整体附着在前缘,限制了流场在前缘处的泄露,具有明显的乘波效应。图6给出了尖头乘波体后缘截面的压力分布,展示了设计激波曲线与CFD模拟结果的对比,激波形状除在转折处存在误差外在大部分区域拟合得都很好。 图7和图8分别给出了钝头乘波体下表面等压线和激波曲线的对比,依然吻合较好,验证了设计方法和性能快速预估方法的有效性,钝头乘波体的气动力结果对比如表3所示。 表1 设计状态和变量Table 1 Design states and variables 表2 尖头乘波体CFD气动力验证Table 2 CFD aerodynamic force validation of cusp waverider 图5 尖头乘波体下表面区域等压线Fig.5 Pressure contour lines under lower surface of cusp waverider 图6 尖头乘波体设计激波(‘∘’)与CFD激波对比Fig.6 Comparison between design shock wave (‘∘’) and CFD shock wave of cusp waverider 图7 钝头乘波体下表面区域等压线Fig.7 Pressure contour lines under lower surface of blunt waverider 图8 钝头乘波体设计激波(‘∘’)与CFD激波对比Fig.8 Comparison between design shock wave (‘∘’) and CFD shock wave of blunt waverider 表3 钝头乘波体CFD气动力验证Table 3 CFD aerodynamic force validation of blunt waverider 乘波体设计与CFD结果的主要误差存在于圆和直线的转折处,本文未严格按照NURBS曲线的曲率设定锥形流,而是使曲率逐渐过渡,这样处理保证了过渡段的曲面光滑,但对乘波体的气动性能有一定的影响,在转折处曲率的设定有待进一步探索。 2.2 低速性能优势分析 本文的设计方法允许指定乘波体的平面形状参数。通过不同后掠角组合生成兼顾高超声速和低速性能的乘波体外形,是一种很有价值且可行的思路。 以钝头乘波体外形为例,考察双后掠乘波体在低速状态的性能优势。设计状态为Ma=8.0,高度为30 km,钝头度ζ=0.3,ω=0.2,β=12°,给定λ1为70°,λ2取值为30°、40°、50°、60°、70°,见图9,其中λ2=70°的外形即单后掠乘波体外形,可以作为性能分析的对比外形。考虑低速和起降性能,考察状态为Ma=0.4,高度为0 km。 图9 测试乘波体外形Fig.9 Views of test waverider 表4 乘波体在高超声速状态的性能Table 4 Hypersonic performances of waveriders 表4给出了所选外形在设计状态(高超声速Ma=8,高度为30 km)的性能,当λ2降低时,高超声速状态的高升阻比特性予以保持,其升阻比不但未下降,还有所上升;容积率τ有所下降,但机身部分保持不变,有效装载空间基本降低很少,因此仍在可以接受的范围内。 图10(a)给出了不同后掠角组合的乘波体在亚声速状态升阻比随迎角的变化,可以看到,当λ2减小时,升阻比曲线有了很大程度的提高。底阻在低速状态的影响非常巨大,实际设计中需要对后体进行修形减阻,同时高超声速飞行器一般将尾喷口放置于飞行器底部,因此在初步估算时可以不考虑底阻。图10(b)给出了不考虑底阻时升阻比的变化,减小第二后掠角会增强低速性能,提高低速状态的升阻比。 图10 不同后掠角组合对低速升阻比的影响Fig.10 Effect of different sweep angles on low-speed lift drag ratio 以λ1=70°,λ2=50° 外形为例,高超声速阶段的升阻比为5.577,低速阶段升阻比为3.5(考虑底阻)或15(不考虑底阻),容积率为0.136,可以看到气动性能可以兼顾低速和高速状态,这为宽速域大空域飞行器的气动外形设计奠定了良好的基础。 2.3 纵向稳定性优势分析 飞行器的纵向稳定性与平面形状关系很大,而双后掠乘波体设计方法可以指定平面形状参数,因此适当设计可以改善纵向稳定性。本节选择2.2节中的系列外形,使用CFD计算高超声速(Ma=8,高度为30 km)和低速(Ma=0.4,高度为0 km)状态下不同迎角的气动性能,分析平面形状对乘波体纵向稳定性的影响。通过3种判据考查双后掠乘波体在高超声速纵向稳定性方面的性能优势。 1) 一般飞行器设计中将重心布置于2/3全长处,图11给出了重心在67%处时力矩系数Cm随迎角的变化,可以看到当λ2减小时,纵向稳定性增加。λ2=70° 的外形纵向不稳定,而随着λ2减小飞行器的纵向稳定性逐渐变强,当λ2≤60° 时已经成为静稳定状态,因此减小λ2可以较大程度上增强纵向稳定性,从表5第一行静稳定裕度的变化也可以看到这一趋势。纵向稳定性可以根据气动焦点(Aerodynamic Center, AC)与重心的位置判定,当重心在气动焦点之前时,飞行器是纵向稳定的。从表5可以看出,气动焦点位置随λ2减小不断后移,说明了纵向稳定性的增强。 2) 减小λ2使得飞行器后体部分面积增加,这给重心的布置带来难度,因此本文考察了乘波体形心(Center of Configuration, CC)与气动焦点随λ2的变化趋势以对纵向稳定性进行分析。从表5中看到随着λ2的减小,形心的后移速度小于气动焦点的后移速度,气动焦点与形心的位置差(表5最后一行)由λ2=70° 的-7.83%拉近到λ2=30° 时的-3.88%,因此减小λ2使得气动焦点的位置相对于形心更加后移,这使得重心布置于气动焦点之前更加容易。从这一角度可以确认飞行器的纵向稳定性随λ2减小而增强。 图11 高超声速状态力矩系数随迎角的变化Fig.11 Variation of moment coefficients with angle of attack in hypersonic state 表5 改变λ2对高超声速纵向稳定性的影响Table 5 Effect of λ2 on hypersonic longitudinal stability 3) 在气动布局的初始设计阶段,有时重心位置难以确定,可以通过计算纵向压心PC位置随迎角的变化来判断飞行器的静稳定特性。图12给出了压心随迎角的变化曲线,当λ2<60°时,随迎角增大压心位置存在后移的趋势,在迎角受到扰动发生变化后能产生回复力矩,保证了飞行条件下的纵向静稳定性。而λ2较大时,压心前移,静稳定性不能保证。 表6给出了低速状态下纵向稳定性与设计参数λ2之间的变化关系,可以看到,在低速状态,双后掠乘波体的性能变化趋势与高速状态相同。 与高超声速状态相比,在低速阶段飞行器的纵向稳定性明显较劣,由表6可以看到,当重心布置在67%时,直到λ2减小到30° 才处于静稳定状态。从图13也可以看到飞行器的压心随迎角都是前移的,这导致气动焦点的位置非常靠前。但仍然可以看到,随着λ2的减小,纵向稳定性的改善趋势非常明显,从λ2=70° 减小到30°,形心位置后移3.8%,而气动焦点位置后移了9.07%,因此在低速状态下改变λ2仍然可以提高纵向稳定性。λ2过小,飞行器的容积率很低,影响了工程实用性,因此λ2取值不能太小,在表5的设计中,选择λ2=40°~50° 左右是可行的。 图12 高超声速状态压心位置随迎角的变化 Fig.12 Variation of pressure centers position with angle of attack in hypersonic state 表6 改变λ2对低速纵向稳定性的影响Table 6 Effect of λ2 on subsonic longitudinal stability 高超声速与低速状态的气动焦点位置差异较大,以λ2=50° 外形为例,Ma=8时气动焦点在乘波体全长的70.70%处,Ma=0.4时气动焦点位置在63.36%处,两者相差7.34%,这是非常大的差距,在之后的飞行器设计中需要特别注意。 图13 低速状态压心位置随迎角的变化 Fig.13 Variation of pressure centers position with angle of attack in subsonic state 2.4 涡效应非线性增升 涡的产生在于流体遭遇突变或静止流动突然被扰动。双后掠角乘波体可以得到前缘突变的乘波体外形,这为利用涡增强升力提供了条件。根据Miller和Wood的研究[19],增强涡升力有两种方法,在给定马赫数的情况下增加迎角,或者增加前缘后掠角。 随着马赫数的升高,激波越来越占据主导地位。为了在高马赫数下产生涡升力,增加λ1生成类似于边条翼的涡生成装置。本文选择在Ma=5、高度为20 km状态下生成带涡生成装置的涡升力外形,见图14(a),第一后掠角为70°,第二后掠角为50°,图14(b)用70° 定后掠角乘波体作为对比外形。 升力系数随迎角的变化如图15所示,随着迎角增加,涡升力乘波体升力的非线性增长很明显,而定后掠角外形的升力则几乎为线性。带涡生成装置的外形从迎角为4° 开始具有非线性增升效果,而这种非线性增升在α=10° 时有接近10%的升力增加,效果非常可观。 涡效应增升可以初步解释如下:随着迎角增大,涡效应逐渐增强,由涡诱导的低压区域逐渐增大,上表面压力减小,尤其是涡生成装置的影响区域压力减小更多,这带来了较大的非线性升力增加。除了增加涡生成装置,将上表面设计为下凹面也可以增强涡升力,具体内容可以参考文献[20]。在高超声速阶段,飞行器上表面的分离情况非常复杂,其涡效应的生成、发展以及影响因素需要深入研究。 图14 带涡生成装置的外形与定后掠角外形Fig.14 Shapes with vortex generation configuration and fixed sweepback 图15 涡升力乘波体升力系数随迎角的变化 Fig.15 Variation of vortex-lift waverider lift coefficients with angle of attack 本文拓展密切锥乘波体设计方法后提出了双后掠乘波体概念,并使用NURBS表达设计曲线,提高了设计方法的灵活性,保证了乘波体外形的光滑和可控。使用CFD手段验证了设计方法的有效性,同时分析了双后掠乘波体在低速状态、纵向稳定性和涡效应方面的性能优势,为宽速域大空域乘波体的工程化实用提供了新的思路。本文首次尝试双后掠乘波体设计分析,未来研究中还有几个问题需着重考虑: 1) 从CFD分析可以看到,不同曲线过渡区域激波形状的吻合情况不好,需要对此区域进行曲率控制以精确模拟乘波性能。 2) 高超声速和低速阶段气动焦点的位置差异较大,在飞行器设计中应研究减小不同速域气动压力位置差别的方法。 本文工作使用自由流面生成上表面,在后续工作中需要研究更合适的上表面生成方法,并探索涡升力与上表面之间的关系。 [1] NONWEILER T R F. Aerodynamic problems of manned space vehicles[J]. Journal of Royal Aeronautical Society, 1959, 63: 521-530. [2] JONES J G, MOORE K C, PIKE J, et al. A method for designing lifting configurations for high supersonic speeds using axisymmetric flow field[J]. Archive of Applied Mechanics, 1968, 37(1): 56-72. [3] RASMUSSEN M L. Waverider configurations derived from inclined circular and elliptic cones[J]. Journal of Spacecraft and Rockets, 1980, 17(6): 537-545. [4] 乐贵高, 马大为, 李自勇. 椭圆锥乘波体高超声速流场数值计算[J]. 南京理工大学学报(自然科学版), 2006, 30(3): 257-260. LE G G, MA D W, LI Z Y. Computation of hypersonic flowfields for elliptic-cone-derived waverider[J]. Journal of Nanjing University of Science and Technology (Natural Science), 2006, 30(3): 257-260 (in Chinese). [5] 刘传振, 白鹏, 陈冰雁. 三维流场乘波体快速设计方法及多目标优化[J]. 宇航学报, 2016, 37(5): 535-543. LIU C Z, BAI P, CHEN B Y. Rapid design and multiobject optimization for waverider from 3D flow [J]. Journal of Astronautics, 2016, 37(5): 535-543 (in Chinese). [6] LOBBIA M A, SUZUKI K. Experimental investigation of a Mach 3.5 waverider designed using computational fluid dynamics[J]. AIAA Journal, 2015, 53(6): 1590-1601. [7] SOBIECZKY H, DOUGHERTY F C, JONES K. Hypersonic waverider design from given shock wave[C]//The First International Waverider Symposium. Maryland: University of Maryland, 1990. [8] SZEMA K, LIU Z, MUNIPALLI R. An efficient GUI design tool for high-speed airbreathing propulsion in tegration: AIAA-2010-4362[R]. Reston: AIAA, 2010. [9] 贺旭照, 倪鸿礼. 密切曲面锥乘波体——设计方法与性能分析[J]. 力学学报, 2011, 43(6): 1077-1082. HE X Z, NI H L. Osculating curved cone (OCC) wave-rider: Design methods and performance analysis[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(6): 1077-1082 (in Chinese). [10] BOWCUTT K G. Optimization of hypersonic waveriders derived from cone flows-including viscous effects[D]. Maryland: University of Maryland, 1986. [11] 王发民, 丁海河, 雷麦芳. 乘波布局飞行器宽速域气动特性于研究[J]. 中国科学: 技术科学,2009, 39(11): 1828-1835. WANG F M, DING H H, LEI M F. Aerodynamic char acteristics research on wide-speed range waverider configuration[J]. Scientia Sinica (Technologica), 2009, 39(11): 1828-1835 (in Chinese). [12] 贾子安, 张陈安, 王柯穆, 等. 乘波布局高超声速飞行器纵向静稳定特性分析[J]. 中国科学: 技术科学, 2014, 44(10): 1114-1122. JIA Z A, ZHANG C A, WANG K M, et al. Longitudin-al static stability analysis of hypersonic waveriders[J]. Scientia Sinica (Technologica), 2014, 44(10): 1114-1122 (in Chinese). [13] STARKEY R, LEWIS M. A simple analytical model for parametric studies of hypersonic waveriders: AIAA-1998-1616[R]. Reston: AIAA, 1998. [14] RODI P E. The osculating flowfield method of wave-rider geometry generation: AIAA-2005-0511[R]. Reston: AIAA, 2005. [15] RODI P E. Geometrical relationships for osculating cones and osculating flowfield waveriders[C]//The 49th Aerospace Science Meeting. Reston: AIAA, 2011. [16] 段焰辉, 范召林, 吴文华. 定后掠角密切锥乘波体的生成和设计方法研究[J]. 航空学报, 2016, 37(10): 3023-3034. DUAN Y H, FAN Z L, WU W H. Research on the methods of generation and design of osculation cone wa-verider with constant angle of sweepback[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(10): 3023-3034 (in Chinese). [17] PIEGL L A, TILLER W. The NURBS book[M]. 2nd ed. New York: Springer-Verlag, 1997: 202-227. [18] CORDA S, ANDERSON J. Viscous optimized hyper sonic waveriders designed from axisymmetric flow fields: AIAA-1988-0369[R]. Reston: AIAA, 1988. [19] MILLER D S, WOOD R M. Lee-side flow over delta wings at supersonic speeds[J]. Journal of Aircraft, 1984, 21(9): 680-686. [20] RODI P E. Vortex lift waverider configurations[C]//The 50th Aerospace Science Meeting. Reston: AIAA, 2012. (责任编辑: 李明敏) Design and property advantages analysis of double swept waverider LIUChuanzhen,BAIPeng*,CHENBingyan ChinaAcademyofAerospaceAerodynamics,Beijing100074,China Based on the design of osculating cone waverider, the concept of double swept waverider is proposed. The relationships between design parameters and configuration parameters are derived. Employing the non-uniform rational B-spline (NURBS) to represent the design curve including circular arc and straight line to aid the waverider generating, this paper develops the method for creating the waverider with controllable configuration parameters, including the blunt head area, the sweep angle and the swept area. The computational fluid dynamics technology is applied to validate the effect of the design method, and the advantageous performances of the waverider are also studied. Results show that with appropriate configuration, the waverider has advantageous performances in subsonic characteristics, aerodynamic stability and nonlinear vortex lift, while maintaining the high hypersonic performance. The method provides a novel way to design the wide-velocity-range hypersonic vehicles. waverider; double swept; subsonic characteristics; stability; vortex lift 2016-09-21;Revised2016-10-10;Accepted2016-11-07;Publishedonline2016-11-151556 URL:www.cnki.net/kcms/detail/11.1929.V.20161115.1556.004.html NationalNaturalScienceFoundationofChina(11672281) 2016-09-21;退修日期2016-10-10;录用日期2016-11-07; < class="emphasis_bold">网络出版时间 时间:2016-11-151556 www.cnki.net/kcms/detail/11.1929.V.20161115.1556.004.html 国家自然科学基金 (11672281) * .E-mailbaipengaero@163.com 刘传振, 白鹏, 陈冰雁. 双后掠乘波体设计及性能优势分析J. 航空学报,2017,38(6):120808.LIUCZ,BAIP,CHENBY.DesignandpropertyadvantagesanalysisofdoublesweptwaveriderJ.ActaAeronauticaetAstronauticaSinica,2017,38(6):120808. http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn 10.7527/S1000-6893.2016.0291 V211.5 A 1000-6893(2017)06-120808-11 *Correspondingauthor.E-mailbaipengaero@163.com
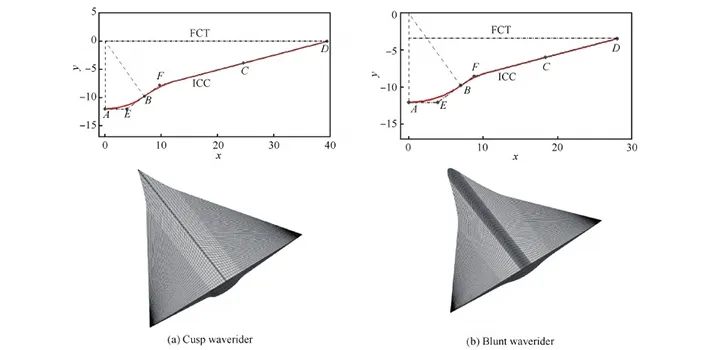
2 性能优势分析



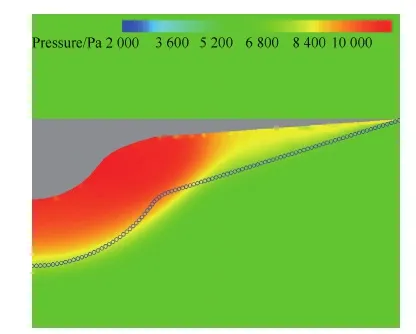



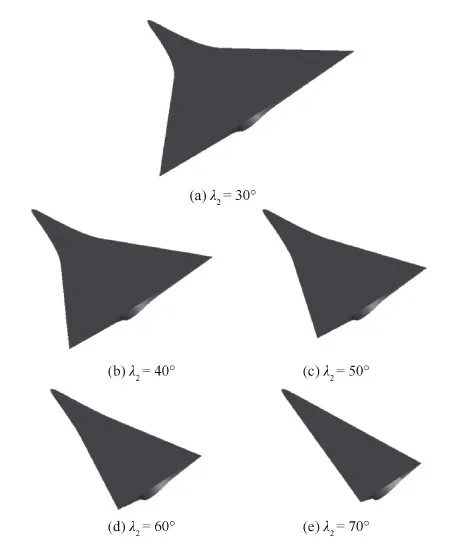
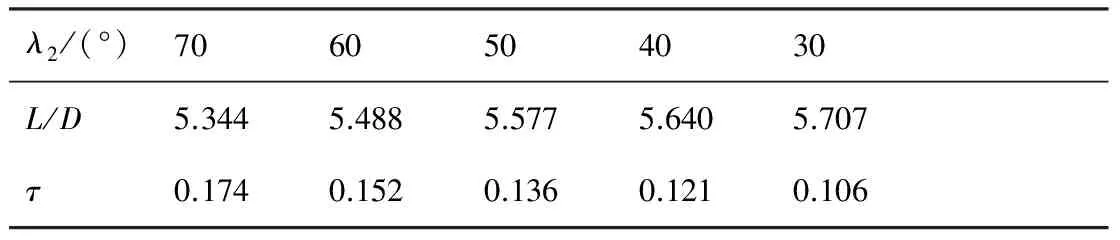





3 结 论
