76Ge 形 变 的 壳 模 型 分 析

金 华

(上海电机学院 数理教学部，上海 201306)

76Ge 形 变 的 壳 模 型 分 析

金 华

(上海电机学院 数理教学部，上海 201306)

在pf5/2g9/2模型空间下，利用壳模型程序MSHELL，基于JUN45有效相互作用对核素76Ge进行了大规模的壳模型计算。计算较好地再现了实验上观测到的能级和E2跃迁概率。通过对计算的γ带能级分布的分析和对受限的Hartree-Fock方法计算得到的等势能面的考察，发现JUN45有效相互作用给出76Ge较软的三轴形变特征。这与实验上76Ge具有刚性三轴形变的分析结果不符，表明现有的JUN45有效相互作用存在一定的缺陷。研究表明，球形壳模型方法适用于中等质量核素形变激发的描述。

大规模壳模型计算； JUN45有效相互作用； 三轴形变； 等势能面

形变是研究原子核集体激发的重要信息[1]。最近，锗Ge同位素的三轴形变引起了实验和理论研究的极大兴趣[2-5]。实验上,通过对表征核素三轴形变的γ带的探测发现，76Geγ带的能级间距分布的相位变化随着自旋的增加，呈现出具有刚性三轴形变的特征;而周围核素γ带对应的能级间距相位变化则与之反相，表现出较软三轴形变的特点，与76Ge形成明显的形变差异[3]。一些基于形变自由度的内禀模型，如三轴转子DF模型[3]和三轴投影壳模型[4]，较好描述了76Ge刚性三轴形变的结构特征。

球形壳模型是原子核结构理论中较为微观的模型，是研究幻核附近核素以及轻核、中等质量核素结构的基本工具[6]。该模型从球形的谐振子势出发构造基矢，借助于计算机的大规模计算，对体系巨大维数的哈密顿矩阵进行对角化，从而得到原子核的波函数和能级[6]。壳模型虽然没有形变参数，但在充分的组态混合之下，同样可以有效描述原子核的集体激发[7]。以76Ge为例，基于唯像的对力+多极力有效相互作用进行的壳模型计算，就被用来研究76Ge的刚性三轴形变[3]。文献[8]中利用拟合pf5/2g9/2壳核区的实验数据得到的JUN45有效相互作用，对该核区开展了壳模型计算，并对相关核素进行了系统地核结构研究，但并没有计算γ带、分析76Ge的形变特征。在上述研究的基础上，本文利用JUN45有效相互作用，对76Ge开展大规模的壳模型计算，在再现实验能级和电磁跃迁概率的基础上，对76Ge的三轴形变进行分析。

1 理论模型

对于76Ge的壳模型计算，以56Ni为冻结的壳芯，截取壳芯上方4个单粒子轨道(2p3/2，1f5/2，2p1/2，1g9/2)作为剩余的价核子激发的模型空间。在JT表象下，体系的哈密顿量可写成二次量子化的形式，即

(1)

式中，ε和j分别为单粒子轨道的能量和角动量；C†和C为产生算符和湮灭算符，其下标为描述单粒子态的一套量子数；V(jajb;jcjd:JT)为反对称化的剩余两体相互作用矩阵元，其中,J和T为两核子总角动量和同位旋，对应的z轴分量分别用M和Tz表示,a、b、c、d为单粒子轨道；而二粒子态产生算符A†则定义成

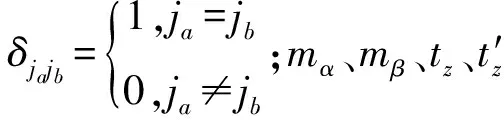
壳模型计算中，单粒子能量往往可通过实验值获取。两体相互作用矩阵元一般有3种途径决定：① 基于唯像核力的计算[9]；② 从裸的核核散射势出发，利用多体微扰理论加G矩阵或Vlow-k方法获取[10]；③ 拟合已有的实验数据得到[8]。本文计算中采用的JUN45有效相互作用，正是拟合了pf5/2g9/2壳核区已有的实验能级获得的，相应的单粒子能量和两体相互作用矩阵元的数值详见文献[8]。由于JUN45有效相互作用的两体相互作用矩阵元具有质量依赖[8]，因而,在76Ge的计算中，其数值需要乘以标度因子(76/58)-0.3。

在确定了相互作用后，便可以构造基矢。采用Lanczos方法对式(1)对应的哈密顿矩阵对角化，得到能量本征值和波函数[6]。大规模的壳模型计算有M-scheme和J-scheme两种构造基矢的方法[6]。本文采用基于M-scheme方法的壳模型程序MSHELL来对76Ge进行大规模壳模型计算。在计算E2跃迁概率时，取质子的有效电荷eπ=1.5e，中子的有效电荷eν=1.1e[8]，其中，e为电子电量。大规模壳模型计算的具体方法见文献[6]，本文不再赘述。

为了考察76Ge的形变，引入受限的Hartree-Fock方法[11-12](CHF)，得到式(1)哈密顿量在价核子总角动量I下具有轴对称β形变和三轴γ形变的CHF态|β,γ,I〉，求出能量期望值〈β,γ,I|H|β,γ,I〉，便可在β-γ平面下，通过绘制等势能面图判断76Ge的形变情况。

2 计算结果与讨论

确定76Ge在模型空间下激发的价核子数目，指定计算的自旋态的角动量I和宇称P，并将JUN45有效相互作用的单粒子能量和两体相互作用矩阵元输入壳模型程序MSHELL，将哈密顿矩阵对角化，便可以计算得到76Ge在某一自旋态下的波函数|IP〉、相应的激发能量E(IP)和价核子在轨道上的占有数。本文中，计算了76Ge激发能在6 MeV以下正、负宇称的能级，并与文献[3]中的实验能级作比较，如图1所示。

图1 76Ge理论计算的能级与实验值的比较

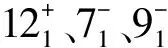
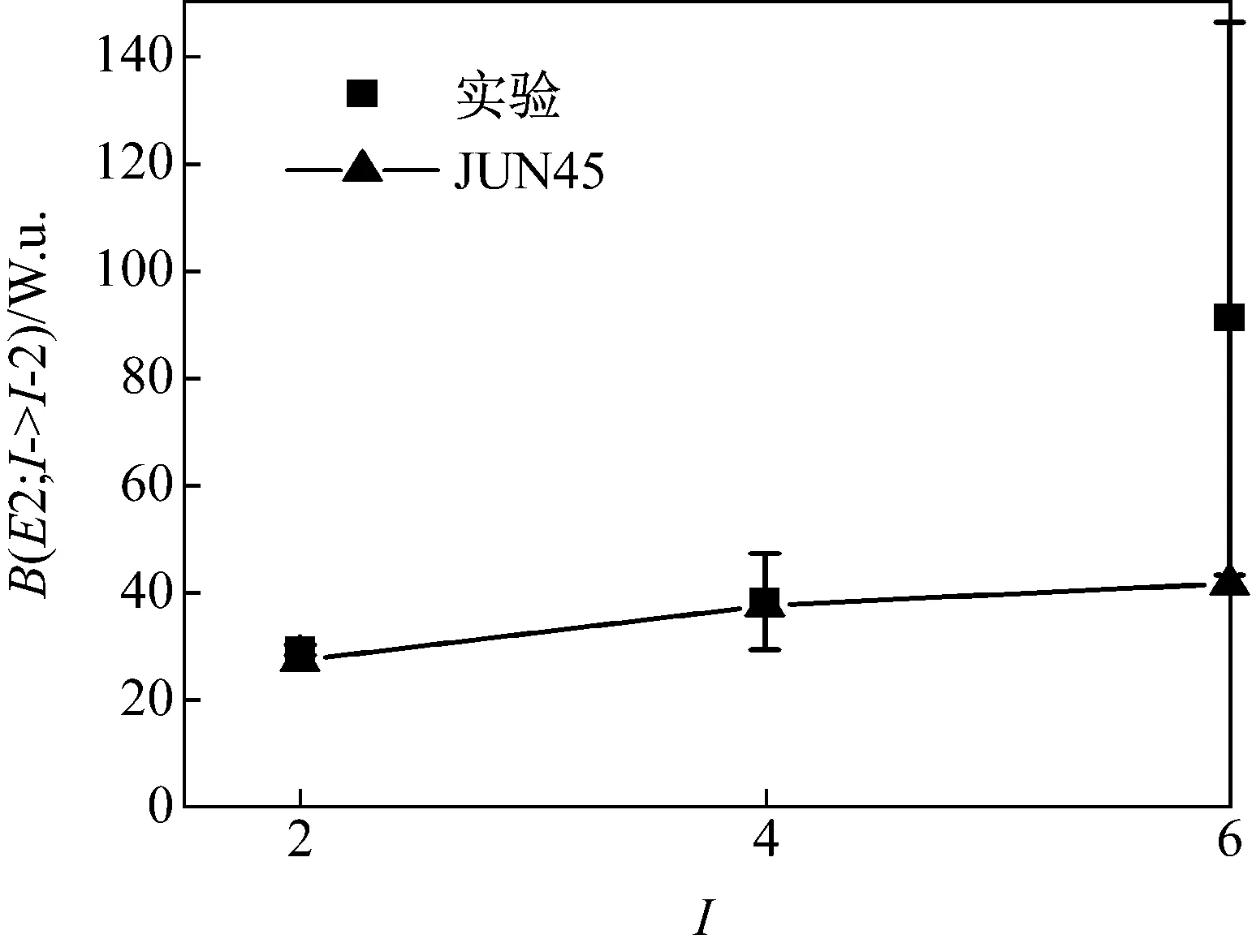
图2 76Ge理论计算的B(E2)值与实验值的比较

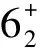
为了区分核素三轴形变的软硬，可对γ带的能级引入变量S(I)进行判断[3,14]，

(3)

当原子核具有刚性的三轴形变时，S(I)呈现出偶数自旋S(I)数值较高、奇数自旋S(I)数值较低的振荡变化；当原子核的三轴形变较软时，S(I)的相位变化与刚性形变的情况相反。图3所示为76Geγ带理论计算的S(I)值与实验值的比较。

图3 76Ge γ带理论计算的S(I)值与实验值的比较

Fig.3 Comparison between the calculatedS(I) values and experimental results forγband in76Ge

由图可见，实验中测得的76Ge的γ带S(I)数值随自旋I变化时，呈现出刚性三轴形变的特征[3];而JUN45有效相互作用计算的γ带S(I)数值在I=5后的振荡行为，表现出较软三轴形变的特征，明显与实验给出的结论不符。这种差异显然是由于理论计算的γ带能级间距分布的不规则性所引起的。

利用CHF方法，图4给出了总角动量I=0时，由JUN45有效相互作用计算的76Ge在β-γ极坐标平面内的等势能面。由图可见，能量最小处位于β≈0.18、γ≈30°方向上一块较平坦的区域内，呈现出较软三轴形变的特点，这与S(I)的分析结果一致，表明JUN45有效相互作用不能给出76Ge刚性三轴形变的特征；但三轴形变的位置出现在γ≈30°方向上，该结果与文献[3]中内禀模型给出的结论相同。

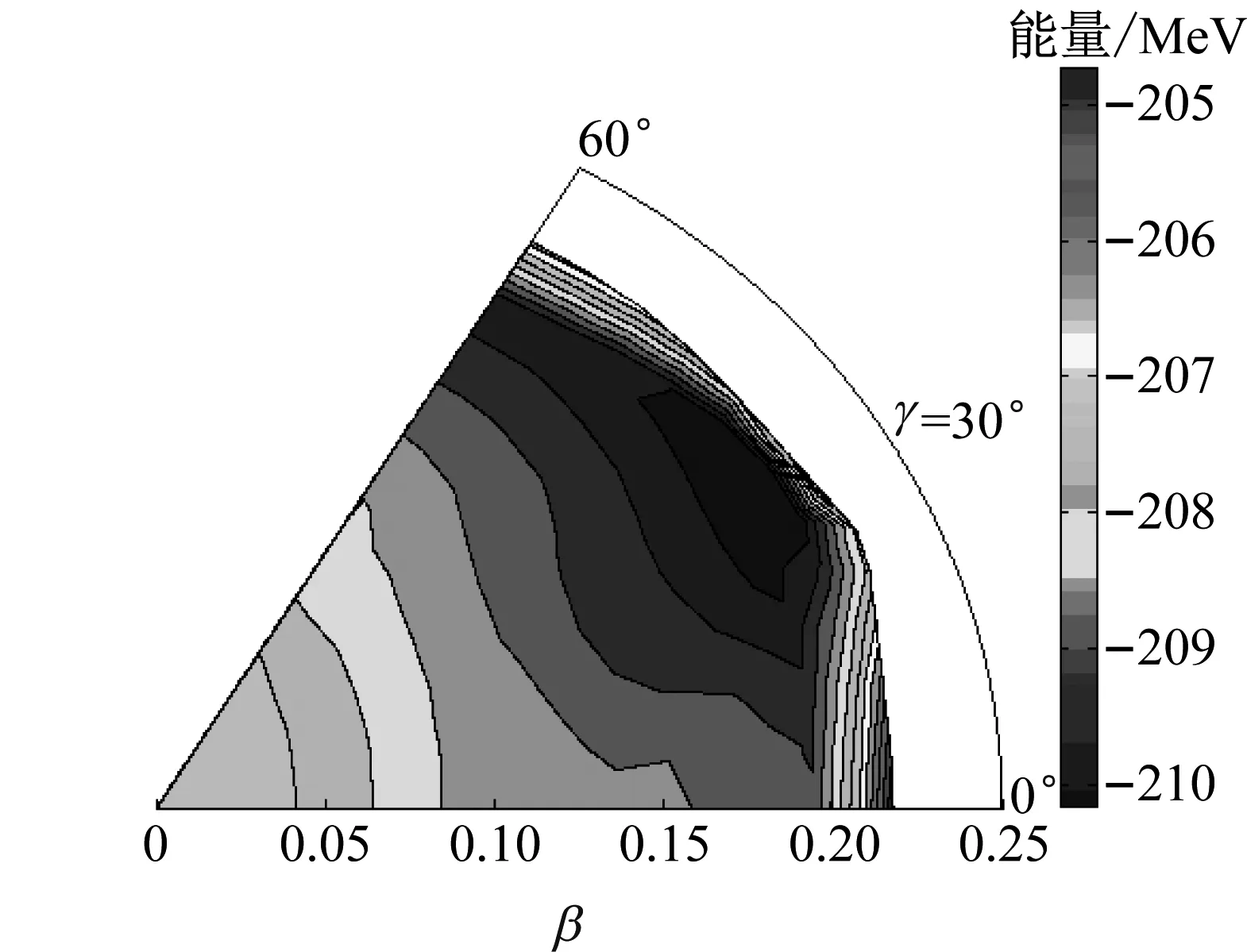
图4 I=0时，理论计算的76Ge的等势能面

3 结 论

[1] 宁平治，李磊，闵德芬.原子核物理基础：核子与核[M].北京：高等教育出版社，2003:412.

[2] LETTMANN M，WERNER V，PIETRALLA N，et al. Triaxiality of neutron-rich84,86,88Ge from low-energy nuclear spectra [J]. Physical Review C，2017，96(1)：011301.

[3] TOH Y，CHIARA C J，MCCUTCHAN E A，et al. Evidence for rigid triaxial deformation at low energy in76Ge [J]. Physical Review C，2013，87(4)：041304.

[4] BHAT G H，DAR W A，SHEIKH J A，et al. Nature ofγdeformation in Ge and Se nuclei and the triaxial projected shell model description [J]. Physical Review C，2014，89(1)：014328.

[6] CAURIER E，MARTNEZ-PINEDO G，NOWACKI F，et al. The shell model as a unified view of nuclear structure [J]. Review of Modern Physics，2005，77(2)：427-488.

[7] 金华，王韩奎，孙扬.丰中子锰同位素的壳模型计算[J].原子核物理评论，2016，33(3)：268-273.

[8] HONMA M，OTSUKA T，MIZUSAKI T，et al. New effective interaction forf5pg9-shell nuclei [J]. Physical Review C，2009，80(6)：064323.

[9] JIN Hua，SUN Yang， KANEKO K，et al. Shell model description with neutrong9/2excitation for neutron-rich57-62Mn isotopes [J]. Physical Review C，2013，87(4)：044327.

[10] CORAGGIO L，COVELLO A，GARGANO A，et al. Shell-model calculations and realistic effective interactions [J]. Progress in Particle and Nuclear Physics，2009，62(1)：135-182.

[11] HARA K，SUN Yang，MIZUSAKI T. Backbending Mechanism of48Cr [J].Physical Review Letters，1999，83(10)：1922-1925.

[12] KANEKO K，MIZUSAKI T，SUN Yang，et al. Shell-model Hamiltonian from self-consistent mean-field model：N= Z nuclei [J]. Physics Letters B，2009，679(3)：214-218.

[13] MUKHOPADHYAY S，CRIDER B P，BROWN B A，et al. Nuclear structure of76Ge from inelastic neutron scattering measurements and shell model calculations [J]. Physical Review C，2017，95(1)：014327.

[14] SUN J J，SHI Z，LI X Q，et al. Spectroscopy of74Ge：From soft to rigid triaxiality [J] . Physics Letters B，2014，734：308-313.

Shell-model Analysis for Deformation of76Ge

JINHua

(Department of Mathematics and Physics, Shanghai Dianji University, Shanghai 201306, China)

Large-scale shell-model calculation is performed for nucleus76Ge with the shell-model code MSHELL using JUN45 effective interaction in the model space ofpf5/2g9/2shell. The calculation well reproduces observed experimental levels andE2 transition probabilities. The energy level distribution for the calculatedγband and potential energy surface are studied, and calculated using the constrained Hartree-Fock method. It is found that the JUN45 effective interaction shows the characteristic of soft triaxial deformation in76Ge. This result does not agree with that of rigid triaxial deformation obtained in experimental studies. Some defects exist in the present JUN45 effective interaction. The paper indicates that the spherical shell-mode method is suitable for description of deformation excitation in medium-mass nuclei.

large-scale shell-model calculation; JUN45 effective interaction; triaxial deformation; potential energy surface

2017 -08 -25

中国科学院高精度核谱学重点实验室开放课题项目资助；上海电机学院学科建设项目资助(16JCXK02)

金 华(1979-)，男，副教授，博士，主要研究方向为原子核结构理论，E-mail: jinhua@sdju.edu.cn

2095-0020(2017)05 -0301-05

O 571.2

A