参悟课程目标 提升教学实效
2017-11-20汤双
汤双

[摘 要] 新课程改革背景下,如何提升初中数学教学效果一直困扰着一线教师. 本文以教学实录为例,从教学艺术、质化艺术、衍生艺术三方面阐述了提升教学效果的具体做法,让学生充分感受学习之乐,领略成长之美.
[关键词] 参悟;提升;课程目标;教学实效
近期,笔者有幸参加南通市名师培养梯队成员会课活动,听了吴老师一堂新授课“平行四边形”. 吴老师严谨的治学态度、精湛的教学技艺和与时俱进的教学理念都让笔者深深折服,也激发了笔者对这堂课的思考.
【教学实录片断1】
师:同学们,这是一个什么图形?(投影图1)
生(齐):平行四边形.
师:我们看一看图1中平行四边形的组成元素有哪些.
生1:有点和线.
师:能说得具体点吗?
生1:有顶点.
师:对,这个多边形有顶点,分别是点A、点B、点C、点D,还有呢?
生2:它有四条边,分别是AB,BC,CD,DA,两组边互相平行,像AB∥DC.
生3:它有两组对角,它们分别相等.
师:很好. 图1中有四个角,分别是∠A,∠B,∠C,∠D,它们是四边形的4个内角. 刚才,生3提到两角的位置关系,例如∠A和∠B是……
生(齐):同旁内角.
师:在平行线中,当两条平行线被第三条直线所截时,会出现同旁内角(如图1中的∠A和∠B). 但在平行四边形中,我们也把∠A和∠B称为邻角,图1中这样的邻角还有……
生(齐):∠B和∠C,∠C和∠D,∠D和∠A.
师:两角之间还有其他的位置关系吗?例如∠A和∠C是什么角?
生(齐):对角.
师:对,这些是我们学过的知识. 今天,我们一起来进一步探究平行四边形的性质.
师:研究一个图形,我们第一步要给它下一个……
生(齐):定义.
教学艺术
学生是学习的主体,教为学服务. 要实现这一目标,教师必须有扎实的基本功,有能灵活调控课堂教学的能力,以及能对学生的学习状态进行准确判断. 小学课本对平行四边形已有介绍,学生都认识它,只是不知道平行四边形的规范化定义,以及如何用符号语言表示出来. 鉴于此,笔者认为本节课的开场可以这样设计:
先画一个图形——平行四边形,“同学们,你们认识这个图形吗?”“认识,是平行四边形. ”“你知道什么是平行四边形吗?”(师生共同讨论,得出定义)“借用它的定义和符号表示,你知道平行四边形有哪些性质吗?”“对边平行,对边相等.”“对角相等.”如此,性质便全变成了几何语言.
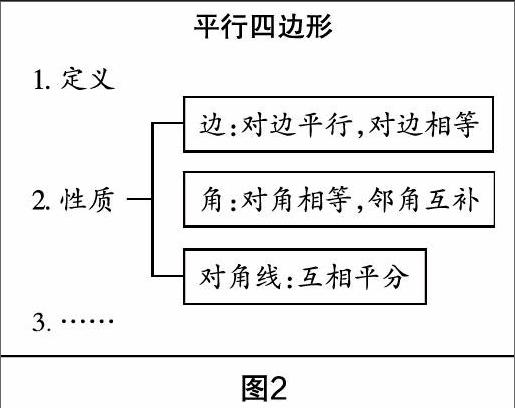
板书设计方面,竖着依次写,条理会更清晰(如图2),师生讨论时学生提到哪一点,就板书哪一点,一方面,针对性强,能体现“学生是主体,我为学生服务”的理念;另一方面,是教学生学习新知的方法,为后续研究特殊的平行四边形做铺垫.
质化艺术
现在,课堂教学讲求高效,那什么是高效?笔者的理解是,以最少的时间获得最大的收获. 那什么是收获?课堂教学的收获不单纯体现为数学知识的拓展与延伸,不单纯地为数学方法的掌握与应用,还涵盖学习技能的习得. 那怎样做才能使学生的收获达到最大呢?笔者认为到达学生的最近发展区就是最大. 即教学中用最少的时间,使知识、方法、能力、情感、态度都达到任教班级学生的最近发展区,产生课堂教学效益.
【教学实录片断2】
师:学习了平行四边形的定义,请同学们看下面这个问题(投影). 如图3,已知四边形ABCD是平行四边形,若∠B=50°,求其他三个角的度数;若∠B=70°,求其他三个角的度数;若∠B=α,求其他三个角的度数.
师:同学们试一试,并把你的解答过程说给大家听.
生1:由已知,因为四边形ABCD是平行四边形,所以AD∥BC. 所以∠A+∠B=180°. 因为∠B=50°,所以∠A=180°-50°=130°. 又因为AB∥CD,∠B=50°,所以∠C=180°-50°=130°. 用同样的方法可求出∠D=50°.
师:非常好!如果∠B=70°,其他三个角的度数又是多少?
生2:……
师:刚才两题中的角是具体值,如果∠B=α,其他三个角的度数如何求?
生3:因为四边形ABCD是平行四边形,∠B=α,所以∠B=∠D. 所以∠D=α.
师:∠B=∠D是你算出来的吗?
生(齐):因为对角相等.
师:你发现了对角相等?为什么?
……
探究平行四边形边与角的性质时,吴老师尊重学生的认知规律,注重知识的生成,用建构思想指导教学,这种教学设计很好. 不过,对于第三小問“当∠B=α时,求其他三个角的度数”,此时既然学生已经发现平行四边形的对角相等,笔者觉得后面的教学过程可以质化一下. 比如,接着学生的思路,“我们今天这节课就是证明平行四边形的对边、对角为什么相等. ”也可以:“同学们,现在我们已经认识了平行四边形的基本元素,有四个角,四条边,就现有的元素请大家从数量关系与位置关系来考量,看看它们之间有怎样的结论,猜想并证明. ”如此一番,学生便马上“上车”了,教学效益生成.
衍生艺术
“授人以鱼,不如授人以渔. ”这是教学的终极目标,也是教育价值最大化的体现. 本课中,平行四边形的性质源于定义的两个特征. 抓住这两点指导学生探究,还可以教会学生研究平行四边形的方法:连接其中一条对角线,将四边形变为两个三角形,进而将研究四边形的边、角关系问题转化为研究三角形的边、角关系问题. 如果往更深一层研究,可以借助电子白板设计教学:利用电子白板“连一连”的功能,在平行四边形内作一条辅助线或两条辅助线,先证平行线间的两个三角形两两全等,并提问“为什么平行四边形有这些性质?”答案显然是因为有“两组对边分别平行”这个前提条件. 再利用电子白板将这个图形绕着对角线的交点旋转180°,此时会发现图形又绕回去了,这说明平行四边形还是中心对称图形,这便进一步向学生渗透了中心对称的知识.
现在的课堂,多媒体技术辅助课堂教学越来越广,教学时,通过多媒体动态直观地呈现平行四边形的性质,既能加强学生对平行四边形性质的理解,又能激发学生的学习兴趣,增强课堂的趣味性.endprint
