基于任意多项式中弧线的单级高效率风扇设计

邱名， 郝颜， 范召林， 江雄， 陈逖

中国空气动力研究与发展中心 计算空气动力研究所， 绵阳 621000

基于任意多项式中弧线的单级高效率风扇设计

邱名*， 郝颜， 范召林， 江雄， 陈逖

中国空气动力研究与发展中心 计算空气动力研究所， 绵阳 621000

为了在压气机通流设计阶段考虑叶片弯掠效应，开发了基于流线曲率法的通流设计程序，提出一种基于四次多项式的任意中弧线叶片造型方法，并推导了任意回转面上的中弧线表达式。以此方法为基础，采用通流设计与叶片造型相互迭代的方式开展大流量跨声速风扇设计研究。此风扇级的设计点为巡航状态，设计流量为155 kg/s、压比为1.54。研究结果表明：在设计状态，此风扇级的总压比为1.545，转子和级效率分别为0.939、0.916；在设计转速下，失速裕度为17%，转子和级最高效率分别为0.945、0.923；在起飞状态，流量接近440 kg/s，效率与巡航状态相当，压比高于巡航状态。

跨声速风扇； 流线曲率法； 叶片弯掠； 大流量风扇； 高效率风扇； 任意中弧线叶型； 多项式中弧线

压气机作为航空发动机的重要核心部件，其性能对发动机的性能、经济性和安全性都有重要影响；而风扇作为压气机的第一级，其损失的大小直接影响到后面各级等熵压缩功的大小。特别是大涵道比发动机，风扇性能对航空发动机的耗油率有着重要影响。因此，高效率、宽稳定工作范围的大流量风扇研究对大涵道比航空发动机研制有重要意义。

20世纪50年代，Wu和Brown[1]提出了著名的三元流理论(又称“两类流面理论”)，将叶轮机内流动分为S1流面流动和S2流面流动。依据两类流面理论，结合S1流面的流动数值计算和S2流面的反问题数值解法，研究者建立起的准三维设计体系；然后再结合弯掠和端弯等设计技术，构成当前的三维设计体系。其中，S2流面的求解对压气机的设计有重要作用。当前的S2求解方法包括流线曲率管流法[2-3]、流线曲率通流法[4]、矩阵通流法[5]和时间推进的欧拉方程通流法[6-8]。流线曲率管流法由Novak[9]提出，计算只涉及叶排间隙区域，通过经验模型考虑损失和堵塞。通过引入叶片体积力，Frost[4]在Novak的基础上提出流线曲率通流法，使得S2流面的计算延伸到有叶区域。

与传统的压气机/风扇设计相比，大流量风扇压比不高，通常采用叶尖切线速度较小的跨声速设计。但风扇尺寸和功率较大，流动具有强三维性，弯掠对其性能有重要影响。但是Frost以及后来一些研究者发展的通流计算方法要么要求计算站垂直于旋转轴，要么要求计算站垂直于子午流线，且不能考虑弯掠效应。为在通流设计阶段考虑风扇/压气机叶片的弯掠影响，Wennerstrom[10]推导了任意计算站上的完全径向平衡方程。该方法通过在叶片前缘和尾缘设置计算站，然后利用叶排内的环量分布规律和熵增计算体积力，通流设计可考虑计算站弯掠的影响。接受Wennerstrom的思想，Hearsey[11]和Law[12]发展了有名的通流计算程序HT0300。

经过通流设计后，再结合一些经验模型可完成轴流压气机叶片构型。当前S1流面的叶型造型大多采用平面叶型生成方法。其思路是先生成平面叶型，再将平面叶型离散，最后转换到回转面上。若回转面为圆柱面，转换后的结果精确；若为其它回转面，转换后有可能使得金属角等参数与通流设计结果不一致。不仅如此，由平面叶型到回转面叶型生成方法较麻烦，同时会失去原有的高阶连续特性。为避免此问题，部分研究者采用基于锥面的叶型造型方法[13-14]。但对于大流量风扇，叶根处S1流面与锥面差别较大；用锥面代替S1流面，常常造成S1流面与轮毂相交。

在过去几十年，中国民用航空发动机主要依靠从国外购买，国内研究较少。近十年以来，中国决定发展具有自主知识产权的民用航空发动机，国内研究者纷纷开展大流量风扇研究。南京航空航天大学的胡骏等[15]开展大涵道比风扇的进气畸变研究;周旭[16]基于简化径向平衡方程，开展某大涵道风扇的改进设计及优化；王志强等[17]开展大涵道比风扇转子优化。哈尔滨工业大学的胡应交[18]基于简化径向平衡方程，开展级压比1.3、涵道比为15的大流量风扇设计。北京航空航天大学的朱芳等[19]基于数值模拟开展涵道比风扇缩尺寸的实验研究。在西北工业大学的高丽敏等[20]提出用长短叶片改善风扇静子的叶尖稠度匹配。这些研究取得很大的进步，但风扇的弯掠设计总是在完成两类流面设计之后再考虑；而且主要依赖CFD进行弯掠分析。

为在大流量风扇的通流设计阶段适当地考虑弯掠影响，本研究依据Wennerstrom推导的完全径向平衡方程开发了一个通流设计程序。同时改进任意多项式中弧线造型，提出任意回转面上的四次多项式中弧线造型方法，满足大流量风扇叶型设计需求。最后进行单级大流量风扇的设计和分析，验证程序的有效性。

1 数值方法及算例验证

1.1 数值方法

为了确保计算和设计结果的可靠性，本文先以NASA Rotor 37为研究对像，探讨数值方法和计算网格的选择，并与实验结果作对比。其中叶片及流道数据来自文献[21]，总体性能的实验数据来自文献[22-23]，流动细节的实验数据来自文献[24]。

在本研究中，计算软件采用PMB3D-Turbo。PMB3D为课题组自编软件，广泛用于歼击机、直升机、螺旋桨飞机和飞船等各类飞行器的数值模拟；已经通过众多工程型号验证。PMB3D-Turbo是在PMB3D基础上进行适应性改造的内流计算软件，支持结构网格、变比热和多级叶轮机械数值模拟。目前，此软件已经过多个标模实验验证；并经过一些非标模的Fluent和Numeca对比验证。PMB3D-Turbo采用有限体积法，多种湍流模型。在本研究中，模拟选用的湍流模型为Spalart-Allmaras模型，空间离散为Roe格式，时间离散为LU-SGS(Lower-Upper Symmetric Gauss-Seidel)格式。同时，采用多重网格和当地时间步长加速收敛。

在本研究中，利用Autogrid 5生成结构网格，采用完全匹配的周期性边界，总网格量约为161万。其中，S1流面的网格及网格拓扑结构如图1(a)所示，叶栅通道被分为7个部分；进口段和出口段为H形网格，共75万网格；通道内为2个J形网格和1个O形附面层网格(见图1(b))，在叶尖间隙区采用蝶形网格(见图1(c))，总网格量为86万。附面层网格的厚度约为2 mm，底层网格与壁面的距离为0.002 mm。计算结果表明，此算例的第1层网格高度y+在0.7左右，且最大y+不超过1.5；网格量增大后，计算结果无明显变化。

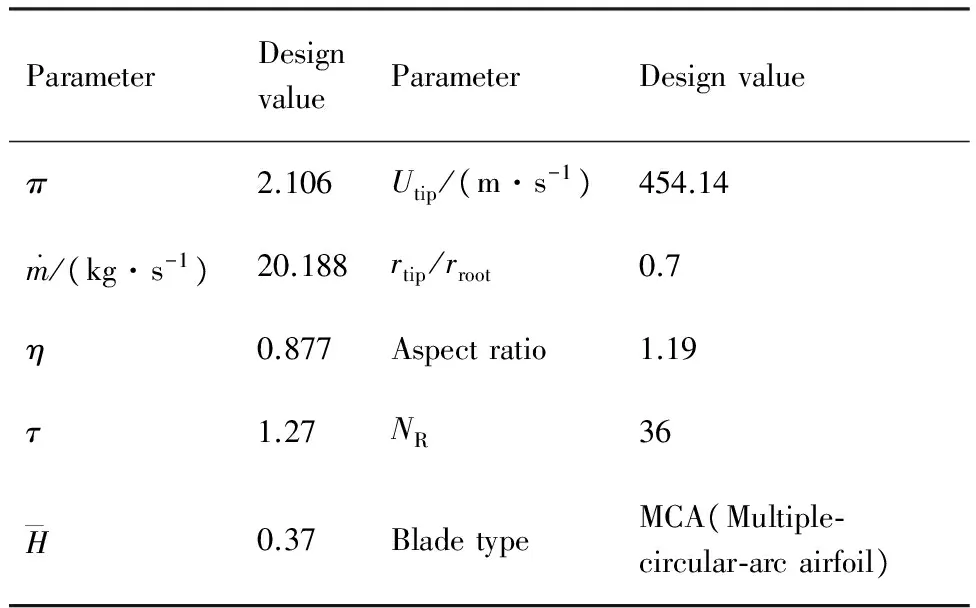
表1 Rotor 37 设计参数Table 1 Design parameters of Rotor 37

求解在绝对坐标系下进行，进口边界给定绝对总温、总压、气流角；出口边界给定叶根处静压，其他叶高静压用简化径向平衡方程计算得到；叶片表面及轮毂设为运动物面边界，无滑移。在本算例中，进口总压为101 325 Pa，总温为288 K，轴向进气。通过调整出口压力，完成整条特性曲线计算。

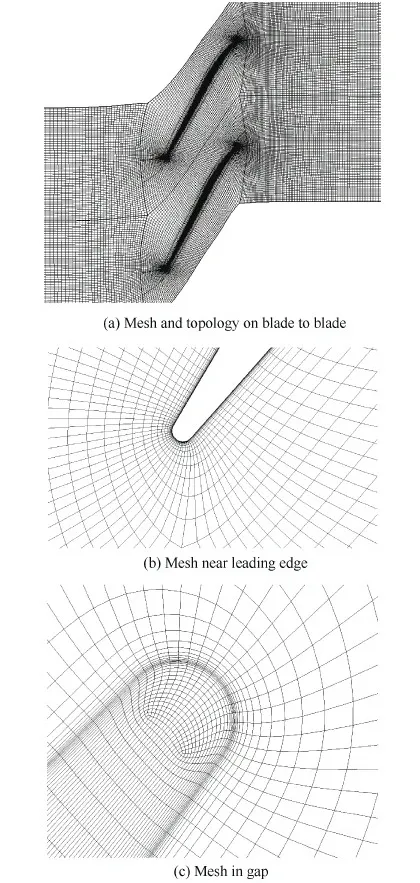
图1 CFD网格 Fig.1 CFD mesh

1.2 Rotor37的计算及实验结果对比

在图2中，用左三角表示实验结果，带棱形的虚线表示CFD计算结果。从图2(a)可以看出，总压比随流量的减小而增大；计算压比略小于实验压比，但计算与实验的结果趋势一致,且误差不大。从图2(b)可以看出,在接近堵塞流量时效率最高，且流量减小后效率降低；在堵塞状态，压比越高，效率越高；计算与实验的结果趋势一致,且误差不大。

在设计点(0.98倍堵塞流量)，周向平均后的展向总压比、总温比分布如图3所示。从图中可以看出，在5%叶高以上，计算结果与实验结果基本一致。在5%叶高以下，CFD计算得到的总压比和总温比比实验值略大；其主要原因在于实验时轮毂部分转动，计算时轮毂全部转动，增大了叶根外的气流角。但总的来说，计算与实验结果基本吻合。图4给出70%叶高的相对马赫数等值线图；计算得到的激波形状、位置、强度与实验结果相当，分离区大小也基本一致；最大误差在于激波前和激波后的最高马赫数差别。从图中可看出，计算得到的激波前最高马赫数1.47，激波后最高马赫数0.97；实验得到的激波前最高马赫数1.50，激波后最高马赫数1.0；两者误差较小，主要来源于测量和结果处理的精度不一致(即小数点后精确的位数)。

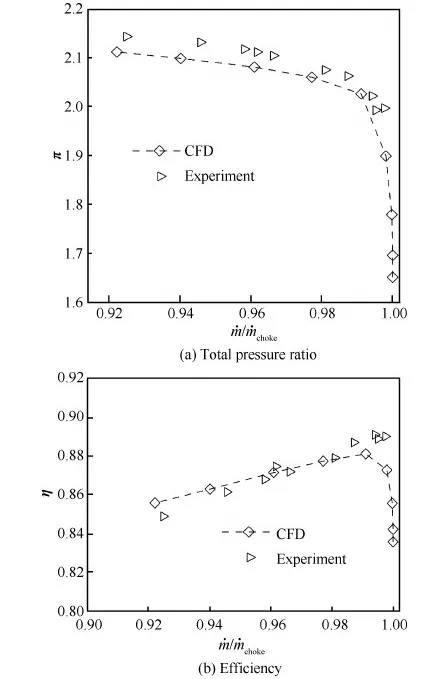
图2 计算与实验的总体性能(Rotor 37) Fig.2 Calculation and experiment overall performance (Rotor 37)

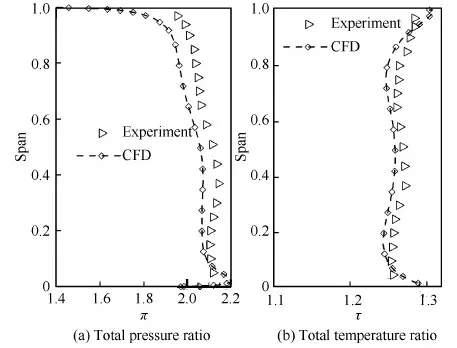
图3 设计点展向参数分布 Fig.3 Distribution of span parameters at design point

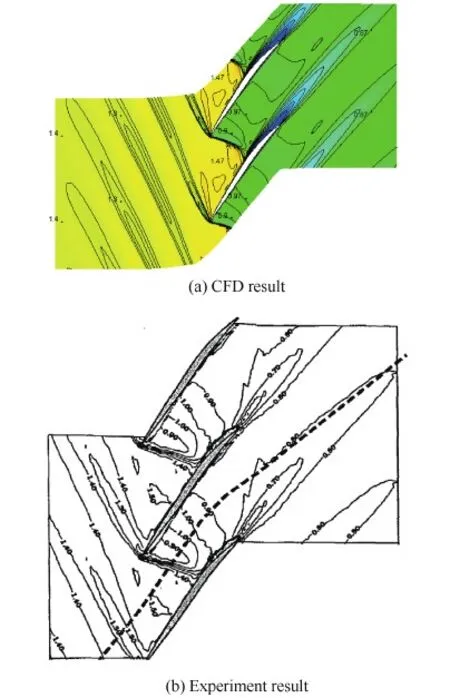
图4 70%叶高的相对马赫数等值线图 Fig.4 Relative Mach number contours at 70% span

2 设计方法

2.1 通流设计

建立图5所示的坐标系，通流设计的主方程(径向平衡方程)为

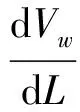
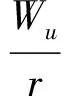
sin(φ+γ)Fw-cos(φ+γ)Fn

(1)

式中：V为绝对速度；W为相对速度；HR为转子焓；s为熵；r为半径；rc为子午流线曲率半径；m为子午面流线的长度；L为计算站长度；φ为子午流流线与轴线的夹角；γ为计算站与径向夹角(见图5(a))；ω为角速度；T为温度；下标w为子午流线方向，n为子午面上垂直于流线的方向，u为周向(垂直于子午面)；Fw和Fn为体积力在w向和n向的分量。其中，

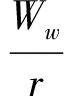
(2)

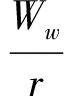
(3)

式中：β′为叶片金属角(即图5(b)中Fs与w向的夹角)，ε为B与l方向的夹角;l为计算站方向。B为L在中弧面的投影；Fs为S2流面上的流线方向。

式(1)推导过程可参照文献[10]，但在文献[10]中体积力的推导有误。此处忽略黏性，体积力与叶片表面压力差等效，并计入落后角的影响。推导思路如下：1)体积力的方向垂直于叶片中弧面，由压力面指向吸力面(即为图5(b)的Fp方向)；Fp为无黏体积力的方向；2)由B和Fs的叉积可求得w、n向的体积力与周向体积力的比值；3)周向体积力与加功量相关，可由环量分布确定。在图5(b)中，Fs处于w-u平面，且与中弧面相切；B处于l-u平面，且与中弧面相切；e为单位向量，ew、en、eu分别为单位向量的3个分量。β′和ε的表达式为

β′=β-δ

(4)

(5)

式中：β为S1流面上的相对气流角，其符号由u的正负确定(x=0,y>0时，u=0)；δ为脱轨角，其符号正负与前缘站相对气流角符号相同。在前缘站δ等于迎角，在尾缘站δ等于落后角；θ为柱坐标系下C点的周向角坐标，按右手系确定正负；x、y、z为相应的笛卡尔坐标(C点位叶片中弧面上，详细定义见图5(c))。对于压气机，若旋转方向为正，转子前缘站气流角的方向为负，静子前缘站气流角的方向为正。

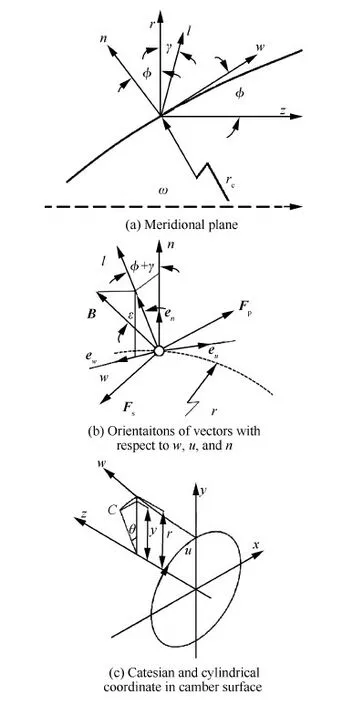
图5 通流设计坐标系 Fig.5 Coordinate system for through-flow design

将式(2)和式(3)代入式(1)并化简可得

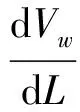
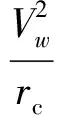
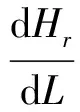
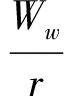
(6)

由于通流设计不包含任何叶片信息，无法直接给出ε。在过去的研究常常假定ε为0(即为直叶片)，从而舍掉ε的相关项(可参照文献[7]的式(34))。但此简化后，通流设计将不能考虑叶片的弯掠信息。为在通流设计中考虑三维效应，本研究保留了此项，并采用通流设计与叶片造型相互迭代的方式完成ε求解。在第一次通流设计时，仍然假定ε为0；完成通流设计后，进行叶片造型，并由造型程序输出各计算站上的ε，堵塞系数等；然后再将造型结果反馈到通流设计中，进行迭代设计。

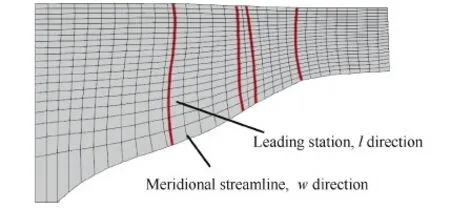
图6 通流设计网格 Fig.6 Mesh for through-flow design

由于计算站的l方向与径向的夹角γ为任意值(γ变化，体积力随之变化)，可在前缘和后缘各设一个计算站(如图6)，从而可在设计和分析中考虑前后掠。同样给定叶片弯掠的数值后，依托于造型程序，可得到对应的ε角，最终转换为体积力。也就是说，依托于体积力的计算，本研究采用的通流设计方法可考虑弯掠的影响。

2.2 叶型设计方法

在完成通流设计后，可得到如图6所示的网格和网格点的流动参数。网格上的子午流线即对应S1流面的母线，三维叶片造型首先需要在S1流面上进行叶型设计。由式(4)可知，给定S1流面的攻角、落后角和脱轨角分布后，可得到各站点的叶片金属角(即得到各计算站处中弧线的切线与轴向夹角)。本研究中初始迎角为0°，初始落后角由卡特公式确定，最后根据CFD结果调整。

为准确表达作者的叶型设计思想，先进行平面叶型中弧线的关系式推导。若将叶型中弧线用k段四次多项式表示，k为后缘站与前缘站的序号之差)，则叶型中弧线方程为：

(7)

式中：z0、zi和zk分别为第j个流面上前缘站、任意站(第i站介于前缘站和尾缘站之间)、尾缘站的流向坐标。对于任意给定的z，满足zi-1≤z≤zi，则

S′(z)=4aiz3+3biz2+2ciz+di=tanβ′

zi-1≤z≤zi

(8)

令

f(z)=Aiz3+Biz2+Ciz+Di=tanβ′

zi-1≤z≤zi

(9)

(10)

由于f′(z0)、f″(z0)、f(z0)和f(z1)已知，解式(10)可得出A1、B1、C1和D1，即确定第1段f(z)关系表达式。在得到第i段fi(z)关系表达式后，节点xi上的一阶导数f′(zi)和二阶导数f″(zi)已知，利用一、二阶导数连续，再次求解式(10)可确定第i+1段的f(z)关系表达式。由f(z)关系表达式可确定式(8)的各项系数，继而得到S′(z)关系表达式。此时，式(7)中的前4个系数ai、bi、ci、di完全确定。结合前缘点处的坐标可确定e1，再依据连续关系确定ei。当Ai≡0时，此方法生成的中弧线与Frost[24]提出的中弧线一致。

一般来说，流线及流线曲率都具有连续、光滑的特性；而任意中弧线的思想就是用考虑落后角的平均流线作为中弧线；因此要求中弧线及中弧线的曲率连续光滑。而本方法得到的中弧线三阶可导连续，其中一、二阶导数不仅连续，而且光滑，这使得中弧线曲率连续且光滑。因此，此方法可生成流线型的中弧线。而过去的任意中弧线造型方法采用三次样条插值，二阶导数连续，但不光滑，不满足流线曲率的光滑特性。这是本方法与文献[24]的中弧线生成方法的区别。为避免繁琐的转换以及由转换带来的金属角误差，同时保持连续光滑的特性，笔者推导了任意回转面上基于四次多项式的任意中弧线叶型造型方法。

在柱坐标系下，由几何关系可得

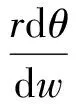
(11)

式中：w为子午面上的流向坐标。对式(11)进一步推导和简化

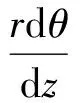
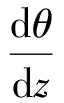
(12)

在式(12)中，z为轴向坐标。按照平面叶型的中弧线造型思路，先用三次样条曲线确定z与tanβ′/rcosφ的关系。此时需要解方程组

(13)

式中：当i=1时，M2=0，M1由最大曲率最小确定；当i>1时，由一、二阶导数连续确定M1和M2。然后由积分关系得到中弧线的表达关系式为

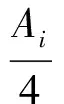
(14)

其中e1由前缘点的坐标确定，ei依据各节点的连续关系确定。此时中弧线上任意点的坐标为(z，r(z),θ(z))。r(z)是半径和轴向坐标的关系式，用三次样条对通流设计的离散流线坐标进行插值可得到。

3 结果与分析

3.1 设计参数

在此研究中，风扇的进口总温为248 K，总压为35 200 Pa。此参数对应11 km高空、飞行马赫数为0.85，进气道总压恢复系数为0.967(雷诺数约为5.7×106)。 详细设计参数见表2，采用等外径设计。为控制叶尖分离，外机匣从转子叶尖30%弦长处向下压3.5°。通流设计时，计算站上的流量等于设计流量加储备流量)。在表2中，πD为设计压比；πTH为通流计算的给定压比；NS为静子叶片数。

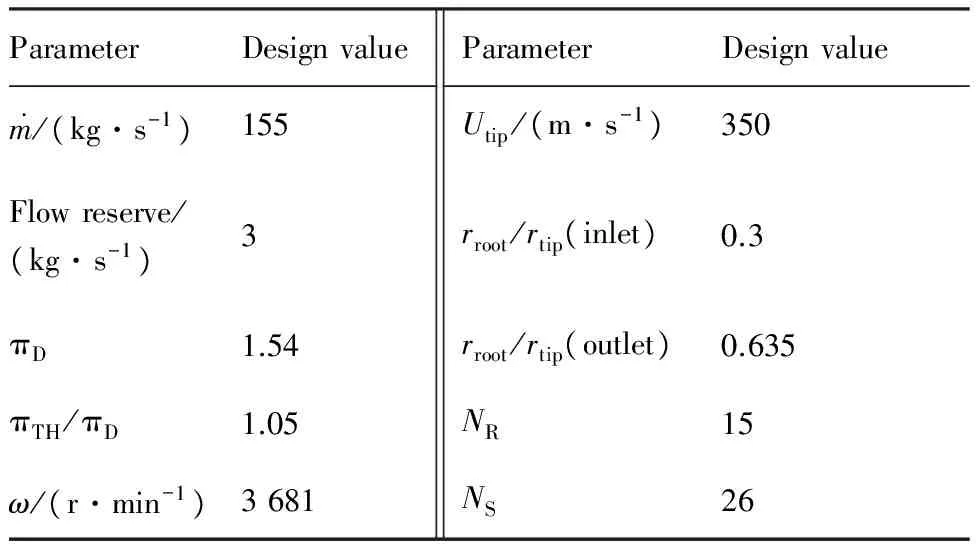
表2 设计参数Table 2 Design parameters

通流设计得到的子午面流线、计算站网格线和马赫数云图如图7所示；径向共采用21根流线，按等流量分配；叶排内设置4个计算站，加上前缘站和尾缘站共6个站；转静叶排间设置一个计算站；转子叶尖马赫数为1.24，在叶尖采用前掠设计。在此设计中，用扩散因子估算叶型损失，用M-L-H(Miller-Lewis-Hartmann)激波模型估算激波损失。通流设计表明，转子效率为0.942，级效率为0.917。

在此研究中，各叶高叶型均采用任意中弧线造型，叶排内的环量分布是中弧线形状的主要决定因素。在过去的研究和设计中，主要依靠经验给定叶排内的环量分布，并认为类似二次函数的环量分布可取得较好的性能。但此结论缺乏理论依据，也从来没有研究者给出普适的二次函数各项系数。而在另一些研究中，研究者认为正弦形式的环量分布效果更好[26]。在此研究中，笔者对比了线性环量分布、下凹的环量分布、上凸环量分布和正弦函数的环量分布。采用线性环量分布时，叶型中弧线接近圆弧，但在前后缘处的曲率有所减小；采用下凹的环量分布时，叶型前段平直，气流转角主要集中在后段；采用上凸环量分布，气流转角主要集中在叶型前段；采用正弦环量分布时，气流转角主要集中在叶型中部。通过CFD的性能分析和对比，此研究最终确定如图8所示的风扇的环量Vu·r分布。此风扇级采用等功设计，轴向进气；转子叶根处的环量采用线性分配，叶尖处的环量采用下凹的曲线分配；其他叶高的环量分布由叶根和叶尖的环量分布进行线性插值。

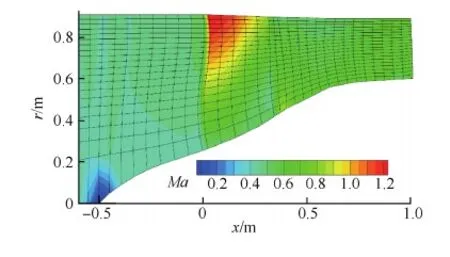
图7 通流设计结果(马赫数) Fig.7 Result of through-flow design (Mach number)

由于采用等功设计，叶根的气流转角较大，叶尖气流转角相对小一些。这使得静子叶根安装角大，叶尖安装角小。若轴向弦长相同，叶根弦长会比叶尖片弦长大。同时，静子叶根处的栅距小，叶尖的栅距大。两者的共同作用使得静子叶根稠度大，叶尖稠度小。这种稠度差别主要由轮毂比决定，轮毂比越小，差别越大，即风扇静子的叶根和叶尖存在较大的稠度差别。为补偿稠度差，静子叶尖的轴向弦长要大一些，叶根的轴向弦长要小一些。基于此思想设计，本研究中的静子在子午流面的形状上宽下窄。最终的造型结果显示，转子叶根稠度为2.5，叶尖稠度为1.65；静子叶根稠度为2.0，叶尖稠度为0.95。

图8 环量分布 Fig.8 Distribution of angular momentum

3.2 设计点性能

基于以上设计结果，采用本文第1节介绍的网格拓扑和数值方法开展数值模拟分析，计算网格量为232万，于静子后缘下游15%弦长处提取数据结果。按流量平均的结果显示，此风扇的级压比为1.545，级效率为0.918，转子效率为0.94。其展向参数分布如图9所示，在90%叶高以下，效率均高于0.9，总压比沿展向变化不大。也就是说，三维CFD的计算结果与通流设计值基本一致，此风扇的转子效率和级效率都较高。

图10给出设计点时不同叶高的马赫数云图，从叶根和叶中均无分离；叶尖存在单道正激波封口，正激波前最大马赫数为1.32，没有因激波附面层干扰而发生明显分离；激波形状基本满足M-L-H激波模型[27]。风扇及其静子叶片吸力面的极限流线如图11所示，由于激波与附面层的相互干扰，转子叶尖吸力面存在小分离，但随即再附；叶根没有发生角区分离，但在60%～80%叶高的吸力面尾缘存在小分离；静子完全无分离。

图9 设计点性能 Fig.9 Perfomance at design point

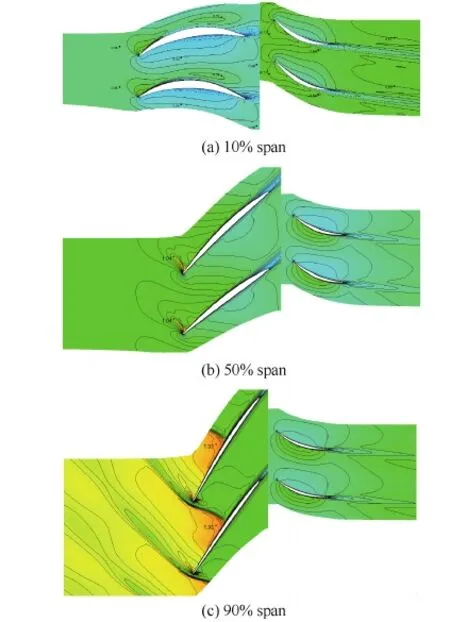
图10 设计点马赫数云图 Fig.10 Mach number contours at design point

图11 吸力面的极限流线 Fig.11 Limit streamline on suction surface

3.3 非设计点性能

保持转速和进口条件不变，通过调整出口压力，直到计算发散，得到图12(a)所示的流量-压比特性曲线。在近失速点，压比为1.58，流量为135.6 kg/s；结合设计点压比(1.54)和流量(155 kg/s)，可求得设计转速下的失速裕度为17%。在本文中，采用如下公式计算裕度。

(15)

式中：下标S为失速点，D为设计点。从图12(a)还可发现，此风扇级具有较宽的稳定工作范围；随着流量越小，风扇转子和级的总压比差别增大。其原因在于流量减小，静子攻角增大，总压恢复系数下降。

图12(b)给出设计转速下的流量—效率特性曲线，此风扇级具有较高的效率。在最高效率点，流量为161 kg/s，级效率达0.923，转子效率达0.945；在近失速点，级效率大于0.85，转子效率大于0.89；若进行优化，此风扇级的效率有可能进一步提升。图13给出近失速点的叶根和叶尖流动，转子叶根前缘附近发生附面层分离，在50%左右弦长再附，在尾缘处又再次分离；叶尖处激波被大大前推，受激波的干扰形成一个小的附面层分离区域；静子叶根和叶尖均出现大分离。也就是说，吸力面大分离和激波前推脱体是此风扇失速的主要原因。

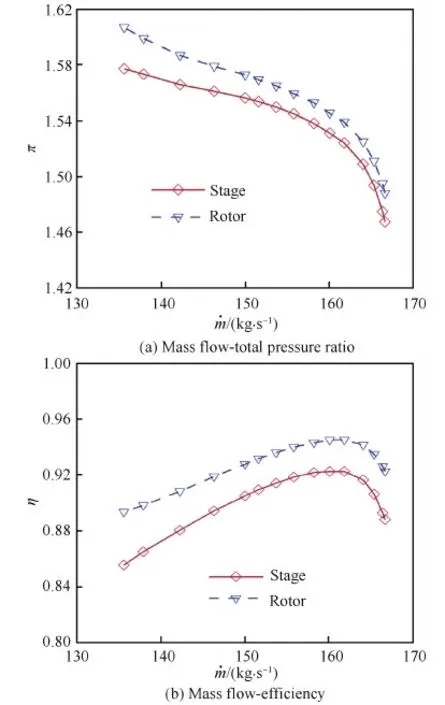
图12 设计转速下的流量-压比和流量-效率特性线 Fig.12 Characteristic of mass flow-total pressure ratio and mass flow-efficiency at design speed

当发动机处于起飞状态时，假定风扇进口总压为101 325 Pa，总温为288 K，风扇转速为1.1倍设计转速(雷诺数约为1.4×107)。此时，此风扇级的流量—压比、流量—效率特性曲线如图14所示，最高效率为0.923，最大压比为1.61。也就是说，此风扇级在起飞状态的效率与设计点相当，起飞状态的压比高于设计点。其原因在于雷诺数增加，附面层流动改善，压比及裕度增大；但来流偏离设计值，效率增加不明显。

图13 近失速点马赫数云图 Fig.13 Mach number contours near stall point

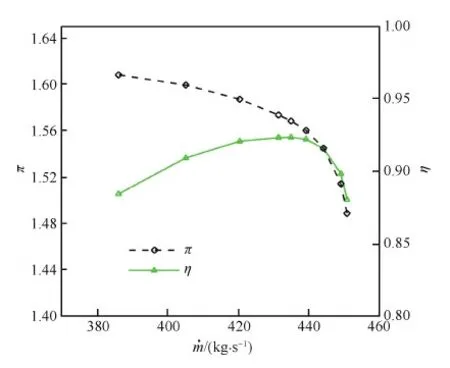
图14 起飞状态的级压比和效率 Fig.14 Stage pressure ratio and efficiency at off state

4 结 论

1) 在设计流量下，此风扇级的总压比为1.545，转子效率0.939，级效率为0.916；叶根、叶中和叶尖均无明显分离。在最高效率点，转子效率为0.945，级效率为0.923，流量为158 kg/s，压比为1.53。在设计转速下，此风扇的失速裕度为17%。在起飞状态，效率与设计状态相当，压比略高于设计状态。

2) 在通流设计中，采用线性环量分布时，得到的中弧线接近圆弧；采用下凹的环量分布时，中弧线前端会逐渐变平。在跨声速风扇设计时，宜采用下凹方式给流向环量分布；且来流相对马赫数越高，要求下凹程度越大；特别是叶尖的超声流动，下凹的环量分布会使激波前马赫数减小。

3) 对于大流量风扇，由于进口轮毂比较小，静子的叶尖稠度和叶根稠度会差别较大。为补偿叶尖稠度，要求静子叶片的叶根轴向弦长小、叶尖轴向弦长大，即要求静子在子午面的投影上宽下窄。

[1] WU Z H,BROWN C A. A general theory of three-dimensional flow in subsonic and supersonic turbomachines of axial-, radial, and mixed-flow types: NACA TN-2604[R]. Washington, D.C.: NACA, 1952.

[2] CREVELING H F, CARMODY R H. Axial flow compressor design computer programs incorporating full radial equilibrium, Part I-Flow path and radial distribution of energy specified (PROGRAM II): NASA CR-54532[R]. Washington, D.C.: NASA, 1968.

[3] CREVELING H F, CARMODY R H. Axial flow compressor design computer programs incorporating full radial equilibrium, Part II-Radial distribution of total pressure and flow path or axial velocity ratio specified (PROGRAM II): NASA CR-54531[R]. Washington, D.C.: NASA, 1968.

[4] FROST D H. A Streamline curvature through flow computer program for analysing the flow through axial-flow turbomachines: RM312-ARC3687[R]. London: National Gas Turbine Establishment, 1972.

[5] MARSH H. A digital computer program for the through-flow fluid mechanics in an arbitrary turbomachine using a matrix method: RM 3509[R]. London: National Gas Turbine Establishment, 1968.

[6] DAMLE S V. Throughflow method for turbomachines using Euler solvers: AIAA-1996-0010[R]. Reston: AIAA, 1996.

[7] 季路成, 孟庆国, 周盛. 叶轮机通流计算的时间推进方法[J]. 航空动力学报, 1999, 14(1): 24-26.

JI L C, MENG Q G, ZHOU S. Time-marching method for through-flow computation of turbomachinery[J]. Journal of Aerospace Power, 1999, 14(1): 24-26 (in Chinese).

[8] 施鑫, 赵拥军, 季路成, 等. 时间推进通流气动设计方法的探索和分析[J]. 工程热物理学报, 2002, 23(增刊): 50-53.

SHI X, ZHAO Y J, JI L C, et al. Explorations and analysis about time-marching through- flow method[J]. Journal of Engineering Thermophysics, 2002, 23(Suppl): 50-53 (in Chinese).

[9] NOVAK R A. Streamline curvature computing procedure for fluid-flow problems[J]. Journal of Engineering for Power, 1967, 89(4): 478-490.

[10] WENNERSTROM A J. On the treatment of body forces in the radial equilibrium equation of turbomachinery: AD-A008127/ARL 75-0052[R]. Washington, D.C.: DTIC/ARL, 1975..

[11] HEARSEY R M. Program HT0300 NASA 1994: D6-81569TN[R]. Washington, D.C.: NASA, 1994.

[12] LAW C H. A computer program for variable-geometry single-stage axial compressor test data analysis (UD0400): AD-A106676/AFWAL-TR-81-2078[R]. Washington, D.C.: DTIC/ARL, 1981.

[13] 闫转运, 成金鑫, 陈江. 多级轴流压气机通流造型一体化设计研究[J]. 工程热物理学报， 2016， 37(6): 1218-1224.

YAN Z Y, CHEN J X, CHEN J. Integrated through-flow and blade shape design of multi-stage axial flow compressor[J]. Journal of Engineering Thermophysics, 2016, 37(6): 1218-1224 (in Chinese).

[14] 《航空发动机设计手册》总编委会. 航空发动机设计手册第8册—压气机[M]. 北京: 航空工业出版社, 1999： 109-114.

“Aero Engine Design Handbook” Editorial Board. Aero engine design handbook, Volume 8-Compressor[M]. Beijing: Aviation Industry Press, 1999: 109-114 (in Chinese).

[15] 胡骏, 赵运生, 丁宁. 进气畸变对大涵道比涡扇发动机稳定性的影响[J]. 航空发动机, 2013, 39(6): 6-12.

HU J, ZHAO Y S, DING N. Investigation of influence of inlet distortion on high bypass ratio turbofan engine stability[J]. Aeroengine, 2013, 39(6): 6-12 (in Chinese).

[16] 周旭. 民用大涵道比风扇叶片气动设计研究[D]. 南京： 南京航空航天大学， 2012.

ZHOU X. Research on aerodynamic design of civil high bypass ratio fan blades[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012 (in Chinese).

[17] 王志强, 沈锡钢, 胡骏. 大涵道比涡扇发动机风扇转子叶片优化[J]. 航空动力学报, 2014, 29(9): 2202-2209.

WANG Z Q, SHEN X G, HU J. Optimization of fan rotor blade in high bypass ratio turbofan engine[J]. Journal of Aerospace Power, 2014, 29(9): 2202-2209 (in Chinese).

[18] 胡应交. 民用大涵道比风扇气动设计[D]. 哈尔滨： 哈尔滨工业大学， 2010.

HU Y J. Aerodynamic design of civilian high bypass ratio fan[D]. Harbin: Harbin Institute of Technology, 2010 (in Chinese).

[19] 朱芳， 陈云永， 卫飞飞, 等. 某民用大涵道比涡扇发动机风扇缩尺试验件气动性能数值仿真[J]. 航空动力学报， 2013， 28(7)： 1539-1548.

ZHU F, CHEN Y Y, WEI F F, et al. Numerical simulation of aerodynamic performance of scaled fan of a civil high-bypass-ratio turbofan engine[J]. Journal of Aerospace Power, 2013, 28(7): 1539-1548 (in Chinese).

[20] 高丽敏, 李瑞宇, 曾瑞慧. 大涵道比涡扇发动机风扇长短叶片结构: 中国, CN104632701A[P]. 2015.

GAO L M, LI R Y, ZENG R H. Short splitter blade structure of high bypass ratio turbofan engine fan: China, CN104632701A[P]. 2015 (in Chinese).

[21] MOORE R D, REID L. Design and overall performance of four highly loaded, high-speed inlet stages for an advanced high-pressure-ratio core compressor: NASA-TP-1337[R]. Washington, D.C.: NASA, 1978.

[22] DUNHAM J. CFD Validation for propulsion system components: AGARD-AR-355[R]. Neuillysurseine: AGARD, 1998.

[23] SUDER K L. Experimental investigation of the flow field in a transonic, axial flow compressor with respect to the development of blockage and loss: NASA-TM-107310[R]. Washington, D.C.: NASA, 1996.

[24] FROST G R, WENNERSTROM A J. Thedesign of axial compressor airfoils using arbitrary camber lines: AD 765165/ARL 73-0107[R]. Washington, D.C.: DTIC/ARL, 1973.

[25] FROST G R, HEARSEY R M, WENNERSTROM A J. A computer program for the specification of axial compressor airfoils: AD0756879/ARL 72-0171[R]. Washington, D.C.: DTIC/ARL, 1972.

[26] 吴宏, 李秋实, 宋亚慧, 等. 风扇通流设计中环量分布形式的探讨[J]. 工程热物理学报, 2008, 29(1):43-45.

WU H, LI Q S, SONG Y H, et al. Effect of swirl distribution on fan through flow design[J]. Journal of Engineering Thermophysics, 2008, 29(1): 43-45 (in Chinese).

[27] MILLER G R, LEWIS J G W, HARTMANN M J. Shock losses in transonic compressor blade rows[J]. Journal of Engineering for Gas Turbines & Power, 1961, 83(3): 235-241.

(责任编辑： 张晗)

URL：www.cnki.net/kcms/detail/11.1929.V.20161014.1350.002.html

Designofsinglestagehighefficiencyfanbasedonarbitrarypolynomialcamberlineairfoils

QIUMing*,HAOYan,FANZhaolin,JIANGXiong,CHENTi

ComputationalAerodynamicsInstitute,ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China

Toadequatelyconsiderthebladeleanandsweepinfluenceoncompressorperformanceinthestageofthrough-flowdesign,athrough-flowdesignprogramisdevelopedbasingonstreamlinecurvatureapproach,andabladeairfoilsgeneratingmethodisintroducedbasingonarbitrarycamberlines.Thecamberlinesisexpressedonarbitraryrotarysurfaceintheinvestigation.Basingonthesemethods,asinglestagetransonicfanisdesigned.Thedesigningisdonethroughtheiterationbetweenthrough-flowdesigningwithbladegeometrygenerating.Thecruisestate,inwhichthemassflowis155kg/sandpressure-ratiois1.54,istreatedasdesignstateintheinvestigation.Theresultsshowthatthepressure-ratiois1.545,androtorefficiencyof0.939,stageefficiencyof0.916atdesignstate.Atthedesignspeed,thestallmarginis17%,andthehighestrotor(stage)efficiencyis0.945(0.923).Themassflowiscloseto400kg/s,andefficiencyincreasesalitter,pressure-ratioobviouslyrisesatoffstate.

transonicfan;streamlinecurvaturemethod;bladeleanandsweep;highmassflowfan;highefficiencyfan;arbitrarycamberlineairfoil;polynomialcamberline

2016-08-01；Revised2016-08-22；Accepted2016-09-26；Publishedonline2016-10-141350

.E-mailqiu_ming_abc@163.com

2016-08-01；退修日期2016-08-22；录用日期2016-09-26； < class="emphasis_bold">网络出版时间

时间：2016-10-141350

www.cnki.net/kcms/detail/11.1929.V.20161014.1350.002.html

.E-mailqiu_ming_abc@163.com

邱名， 郝颜， 范召林, 等． 基于任意多项式中弧线的单级高效率风扇设计J． 航空学报,2017,38(5):120657.QIUM,HAOY,FANZL,etal.DesignofsinglestagehighefficiencyfanbasedonarbitrarypolynomialcamberlinesairfoilsJ.ActaAeronauticaetAstronauticaSinica,2017,38(5):120657.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0262

V231.3

A

1000-6893(2017)05-120657-12