基于图剖分的多块结构网格负载平衡方法
2017-11-20刘宏康阎超林博希赵雅甜
刘宏康, 阎超, 林博希, 赵雅甜
北京航空航天大学 航空科学与工程学院, 北京 100083
基于图剖分的多块结构网格负载平衡方法
刘宏康, 阎超*, 林博希, 赵雅甜
北京航空航天大学 航空科学与工程学院, 北京 100083
负载平衡是影响并行计算性能的重要因素。针对多块结构网格,给出了一种改进的多层次图剖分负载平衡方法。该方法设计了新的网格剖分算法,采用改进的子块分裂方法与图剖分算法的循环调用实现结构对接网格剖分,并通过建立不同物体重叠网格间的连接关系,实现了结构重叠网格的负载平衡。采用2个典型算例对方法进行了对比验证,数值结果表明,子块分裂方法对剖分结果具有重要影响,采用循环调用算法及改进的子块分裂方法能有效地实现计算负载均衡及通信量优化,同时显著减少了网格块数及因虚网格导致的内存需求,有利于提高并行效率。该负载平衡方法与网格拓扑无关,适用于多块结构对接网格及重叠网格,且整体型剖分方式对于多块结构重叠网格具有更好的剖分效果。
计算流体力学; 并行计算; 结构网格; 负载平衡; 图剖分
计算流体力学(Computational Fluid Dynamics,CFD)中通常需要将物理流场离散化为计算网格,其中,多块结构网格(单块为结构网格但各块间的连接关系可以为一一对应或重叠)技术扮演着重要角色,在航空航天、气象预测等领域应用广泛。
随着工程问题日益复杂化,高精度的数值模拟需求对计算格式及网格分辨率提出了更高要求,进而导致计算量急剧增加。受限于串行程序的计算效率,并行计算是解决上述问题的重要手段,而影响并行性能的关键因素之一是计算负载平衡的实现。
当前的CFD并行计算普遍采用“单程序多数据”模式,需要将计算网格映射到分布式存储系统的各个进程上。在复杂实际问题中,计算区域一般由多个大小不等的子块组成,且存在相互间流场信息传递的复杂问题,同时伴随着并行规模的增加,这给结构网格的负载平衡带来了困难。因此,发展适用于复杂实际问题的结构网格负载平衡方法,对实现计算负载均衡及进程间通信成本优化具有重要意义。
现阶段国内外对负载平衡方法的研究较为丰富,提出了一系列启发性算法,如贪婪算法[1]、谱方法[2]、几何剖分方法[3]及图剖分方法[4]等,并已集成至通用软件包,如文献[5-6]等。上述算法对非结构网格具有天然适用性,但无法直接适用于结构网格,且在该方面的研究也相对有限。国外方面,Ytterström[7]最早提出了递归边对分(Recursive Edge Bisection,REB)方法进行网格细分以实现负载平衡,而Rantakokko[8]进一步发展了多层次剖分的负载平衡方法,在一定程度上减少了网格块数。Ahusborde和Glockner[9]重点研究了非规则矩形流场的子块分割算法并进行了流场求解,Djomehri和Biswas[10]则采用REB方法进行了重叠网格的子块分割,并基于Overflow求解器开展求解,对比不同算法并行效果。国内方面,司海青和王同光[11]提出了一种无子块分割的负载剖分算法,李桂波和杨国伟[12]则采用遗传优化算法研究了负载与通信的并行影响,许正等[13]采用负载再分配策略来实现动态负载平衡,并提出近似均分子块分割方法。上述研究往往以对接结构网格为主,难以适用于多块结构重叠网格,并且由于对网格块数的关注不足,存在子块分割过多或剖分效果受网格拓扑、进程数影响较大的缺陷。
本文针对负载平衡方法进行了研究,提出了一种改进的结构网格负载平衡方法。该方法采用网格子块分割及图剖分的循环调用思路,同时改进了子块分裂方法,并通过建立重叠边界关联,将其拓展至多块结构重叠网格。最后,对三段翼30P30N对接网格及翼身组合体DLR-F6 WB重叠网格算例进行数值对比分析,验证本文方法的可行性。
1 控制方程及数值方法
基于格心有限体积法求解控制方程,当不考虑外加热和体力影响时,直角坐标系下三维可压缩Navier-Stokes方程组的守恒积分形式为
(1)
式中:Ω为控制体;S为控制面;n为微元S的单位法向量;Q为守恒变量;Fc为对流通量;Fv为黏性通量。
本文采用多块结构网格,将流场划分为多个计算区块,并在每个区块建立局部计算坐标系,而区块之间的相邻关系采用对接型或重叠型实现。
数值方法包括空间离散方法和时间推进方法,其中,对流项离散采用Roe格式,通过MUSCL (Monotone Upstream-centred Schemes for Conservation Laws)插值实现二阶精度,并采用Mixture限制器消除非物理振荡,黏性项采用二阶中心差分格式,时间推进采用LU-SGS (Lower-Upper Symmetric Gauss-Seidel)隐式方法。湍流模型采用两方程SST (Shear-Stress Transport)模型。
2 负载平衡问题
负载平衡实际上是在并行机或分布式多处理机的各节点之间合理分配计算任务的过程,一般分为静态负载平衡问题和动态负载平衡问题。本文所研究的结构网格负载平衡在开始数值计算前进行网格划分,属于静态负载平衡问题。
为满足CFD并行效率要求,在把计算网格映射到各个进程上时,应使得各进程的网格单元数尽可能接近,且满足进程间需要交换的信息量最小,这种映射一般可视为图剖分问题。
所谓图剖分问题[14],就是把数据间的相互依赖关系抽象成一个图,通常用加权无向图来表示计算和通信关系。加权无向图G={E,V,Wv,We}由顶点集V={v1,v2,…,vn}和边集E={e1,e2,…,em}以及相应顶点权重集Wv={w(v1),w(v2),…,w(vn)}和边权重集We={w(e1),w(e2),…,w(em)}构成,n为顶点数,m为边数,w(vi)为顶点的权重,表示顶点的计算量大小,w(ei)为边的权重,表示通信量大小。


图1 图的两种剖分示意 Fig.1 Schematic diagram of two kinds of graph partition
3 负载平衡方法
现有的图剖分算法(如多水平算法[15]、多尺度KL/FM算法[16]等)对于非结构网格具有天然的适用性,但无法直接用于结构网格的负载平衡实现,需要在上述算法基础上构造具有针对性的负载平衡策略。
对于结构网格,当原始网格子块数目不满足图剖分要求或各子块网格单元数差异大时,剖分往往难以获得理想的负载平衡效果。解决该问题的一种有效途径是对原始网格的细分处理,即通过分裂网格子块,增加子块数目并使得各子块的网格规模减小。
而随着子块的不断细分,网格块数逐渐增加,形成的大量网格子块将给计算效率、稳定性和精度带来影响[17]。在采用虚网格进行内对接边界传值情况下,大量的内对接边界将导致内存、通信量的快速增加,并且在采用隐式时间推进时,网格块的过于细化将弱化隐式求解的优势,不利于收敛。此外,某些高阶或紧致格式求解时,内对接边界本身也会带来精度损失。因此,结构网格的并行剖分需要权衡负载平衡效果与剖分后网格拓扑影响,而这与细分处理方法息息相关。
针对上述情况,借鉴Rantakokko[8]的多层次剖分思想,本文提出了一种改进的负载平衡方法,可适用于多块结构对接网格,并将其推广至多块结构重叠网格。该方法主要包括以下3个方面:全体块的图剖分实现、子块的分裂处理以及对上述2个过程的循环调用实现。
3.1 图剖分实现
图剖分是本文方法的重要组成,通过调用通用图剖分软件包,可直接利用现有成熟算法进行网格块的剖分。因此,本文该部分的工作在于建立适用于图剖分算法的无向加权图。
针对多块结构对接网格,将每个计算网格块视为图的顶点vi,顶点的权重w(vi)取每个块的网格单元数,形成图的顶点集V及其权重集Wv;相应地,相邻块的内对接边界可建立边ei,边的权重w(ei)取内边界面的单元数目,形成图的顶点集E及其权重集We,从而形成完整连通的无向加权图G。关于该无向图G建立的具体描述可见文献[18],此处不赘述。
与对接网格不同,多物体重叠网格在形成插值边界前,不同物体网格间不存在连接关系,此时所建立的无向图是不连通的。
因此,最直观的方法是将各个物体计算网格按照多块对接型网格的剖分方式依次处理,此处称为独立型剖分方法。该方法简单,算法可通用,但随进程数增加,存在子块数目多且部分权重过小的缺陷,对小网格量物体尤为明显。
因此,本文提出了另外一种重叠网格剖分方式,即通过初始网格重叠处理,依据重叠关系在两个不同物体网格重叠区域各取一子块建立连接边,并按重叠边界关系给定边权值,如图2所示,从而保证无向图连通并进行图剖分,该方法称为整体型剖分方法。
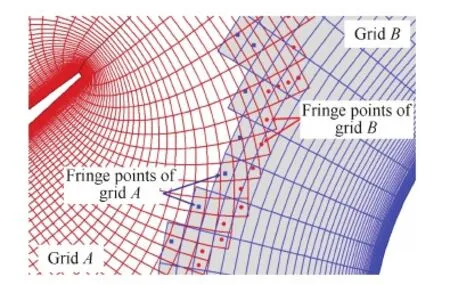
图2 重叠网格边界单元 Fig.2 Fringe points of overset grid
此外,在整个负载平衡实现过程中,由于存在网格块的细分处理,无向图本身是动态的,需要在每次细分处理后建立新的无向图,该建立过程主要采用遍历搜索实现。
3.2 子块的分裂处理
常用的子块分裂方法包括结构型剖分方法[19]及REB方法。前者直接均等分裂原始网格块得到大量子块,而REB方法则通过对最大子块的最大维数方向递归分裂以获得均匀子块。几何剖分方法简单,能快速实现网格的细分,但由于无法预知分裂后的图剖分结果,往往会为了达到较好负载平衡效果而明显增加分裂子块数。
因此,借鉴REB方法的递归思想,本文对子块分裂方法进行改进,将根据各子块权重与平均权重关系来动态地调整子块选取及分裂处理。子块分裂方法的具体改进工作主要围绕分裂子块选取原则及分割方式两个方面展开。
在网格细化过程中,为选取更合适的分裂子块(为便于后文描述,此处称其为寻优子块),其选取原则设计如下:
1) 求得每个进程的平均网格量Wave,并根据负载不均衡率上限ε0,给出子块理想权重范围Wideal=[Wave(2-ε0),Waveε0],同时为避免子块权重过小,给定权重下限值Wmin=Widealσmin。
2) 在每次分裂开始前,对所有子块编号及赋权重,并根据子块权重由大到小进行排序{w1(vi),w2(vi),…,wn(vi)}。
3) 根据步骤2)排序表,由大到小进行判断:当w1(vi)∈Wideal时,该子块无需分裂,选择下一子块继续判断,依此类推,直到找到某子块权重满足wj(vi)∉Wideal且wj(vi)>Wmin,则判定该子块需要分裂;否则不进行子块分裂。
针对子块的分割方式,区别于REB方法的最大维均等二分处理,此处将依据子块拓扑结构及权重关系进行自适应分割,其具体过程为
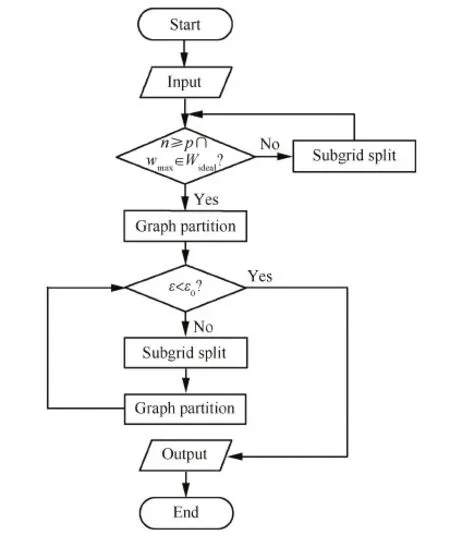
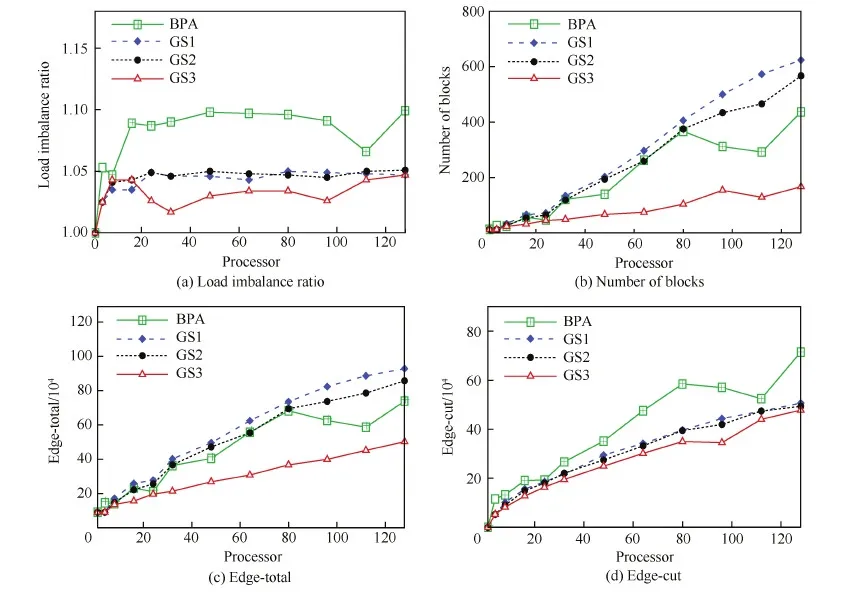
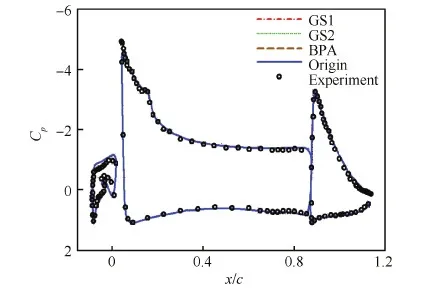
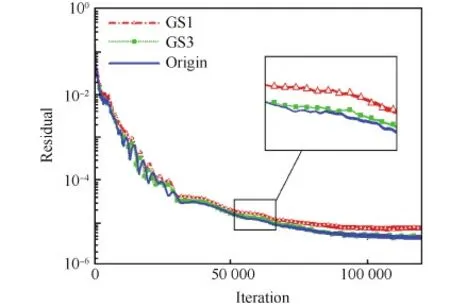
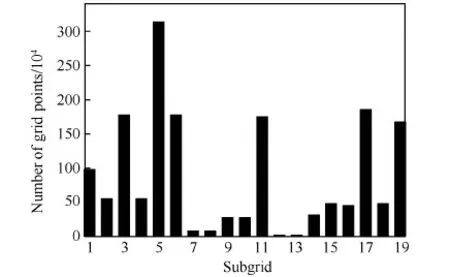
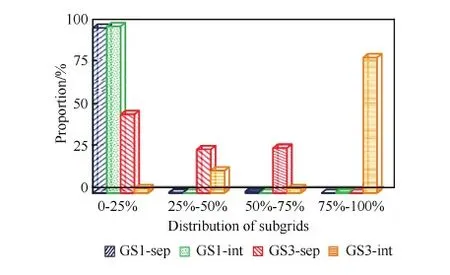
1) 当Wmin 2) 当w(vi)>Wave+Wmin时,按由大到小顺序记子块3个方向维数分别为N1、N2、N3,则最大维数为Nmax=N1。 5) 若步骤4)中条件都不满足,则按步骤1)的分裂方式进行处理。 3.3 图剖分与子块分裂的循环调用算法 在图剖分实现及子块分裂处理基础上,建立合理高效的调用算法是实现负载平衡的关键之一。本文方法采用图剖分算法及子块分裂处理的循环调用,在多层次的细化过程中实现负载均衡度与通信量的优化,且尽可能减少网格子块数。 图3给出了该算法主要流程图,其中n为网格块数,p为计算进程数,wmax为最大子块权重,ε为剖分后负载不均衡率,定义为单个进程最大负载量与平均负载量之比,此处ε0默认取为1.05。 图3 剖分算法流程图 Fig.3 Flow diagram of partition algorithm 为验证本文提出的负载平衡方法的有效性,采用2个典型算例进行了剖分试验,从负载不均衡率、网格子块总数、边界面单元总数(Edge-total)及通信界面单元数(Edge-cut)4个方面对比了不同网格类型下剖分方法的剖分效果。 在对接网格算例中,所用方法包括图剖分-最大子块最大维均等二分法(记为GS1)、图剖分-寻优子块最大维均等二分法(记为GS2)以及图剖分-寻优子块自适应二分法(记为GS3),通过算例分析子块分裂方法对负载平衡的影响,并与采用传统负载平衡算法及不采用负载平衡的结果进行了部分核数下的并行效率对比。所采用的传统负载平衡算法为装箱算法[20],即BPA(Bin-Packing Algorithm)。 在此基础上,结合重叠网格剖分特点,比较了独立型剖分方法(分别记为GS1-sep、GS3-sep)以及整体型剖分方法(分别记为GS1-int、GS3-int)在多块结构重叠网格算例中的表现。 4.1 三段翼30P30N翼型 本算例选取高升翼型30P30N[21]进行负载平衡方法验证与对比,考察不同进程数下的负载平衡效果,并进行了部分状态的并行计算。计算条件为:马赫数Ma=0.2、雷诺数Re=9×106、迎角α=4°。 原始网格总网格量约为855.1万,共包括13个子块(拓扑结构见图4),且各子块网格量分布如图5所示,图中横轴坐标为网格块编号,纵轴坐标为网格量,其中,最大子块网格量约占总网格量的18.6%。 图4 30P30N翼型网格拓扑 Fig.4 Topology of 30P30N airfoil grid 图6给出了GS1、GS2、GS3这3种方法及传统装箱算法在不同进程数下的剖分结果,图中横坐标为进程数。图6(a)为负载不均衡率随进程数变化曲线,可以看到,本文3种负载平衡方法均达到负载不均衡率要求(ε≤1.05),其中GS3整体略优,而BPA所得负载不均衡率明显偏高。图6(b)则为网格子块总数随进程数变化曲线,可见,随着进程数增加,GS1所得网格子块总数快速增加,GS2方法与BPA表现类似,略有减少,而GS3维持着较少且平缓的增长趋势。图6(c)为边界面单元总数及通信界面单元数随进程数变化曲线。由于边界面单元总数与网格子块数正相关,因此该量的变化呈现出与子块总数类似的变化趋势。而在通信界面单元数方面,如图6(d)所示,GS1、GS2两种方法的增长趋势基本一致,GS3方法略有优势,这预示着,通过图剖分算法的通信优化,GS1及GS2方法所产生的大量内边界面单元将分配在同一进程,从而避免了进程间通信量的急剧增加。相比之下,BPA由于缺少对进程间通信量的优化,产生了更多的通信界面单元,即意味着更高的通信成本。 图5 30P30N翼型网格量分布 Fig.5 Distribution of number of grid points of 30P30N airfoil 图6 30P30N翼型不同进程数时网格剖分结果 Fig.6 Partitioning properties as a function of processors for 30P30N airfoil grids 由此可见,本文3种负载平衡方法皆能满足负载平衡要求,而对比结果表明,新的子块选取原则能一定程度地减少剖分子块数,且改进后的子块分割方式体现出了更明显的作用,能够极大地避免子块数过多的缺陷,进而降低因虚网格而额外增加的内存需求。 为比较剖分方法对计算效率的影响,且考虑到原始网格块数限制,对小核数情形进行了并行计算,对比不同负载平衡方法及不采用负载平衡的并行影响。 图7及图8分别为小核数时不同剖分方法及不采用负载平衡(记为NO-LB)的负载不平衡率和并行加速比曲线,其中Np为核数,Nb为原始网格块数。从图中可见,不采用负载平衡时,其负载不平衡率明显偏高,并对并行加速比产生了十分不利的影响。而相比于传统装箱算法,本文的3种方法皆能获得更优的负载不均衡率及并行加速比,其中,GS3方法表现最优。由此可见,本文的新方法在并行计算效率方面具有更佳效果。 图7 负载不均衡率曲线(Np 图8 并行加速比曲线(Np 为进一步研究网格块数对数值计算的影响,对进程数为128时的GS1、GS3及BPA 3种方法的剖分网格进行了并行计算,并与原始网格串行结果进行对比。图9为30P30N翼面压力系数计算结果(Orgin代表原始网格),图中横坐标为机翼表面坐标x与弦长c之比,纵坐标Cp为压力系数,可见,不同网格结果与实验值吻合较好,证实了本文数值计算的正确性。 表1为3套网格的负载不均衡率及子块总数,并给出了并行计算加速比及预测阻力系数CD。可以看到,GS1和GS3方法所得负载不均衡率保持一致,但子块总数相差较大,而BPA所得负载不均衡率及子块总数均较大。从并行加速比来看,GS3剖分方法更有优势,BPA所得并行加速比最低。阻力系数的预测结果表明网格拓扑对计算产生了影响,过于细分的网格使得阻力系数偏离原始网格串行结果更明显。图10及图11则分别给出了GS1、GS3 2种方法及原始网格的计算残差及阻力系数收敛曲线,可以看到,网格的细分使得收敛性有所变差,GS1方法表现得更为明显。 图9 30P30N翼面压力系数分布 Fig.9 Pressure coefficients distribution on surfaces of 30P30N airfoil 表1 进程数为128时的剖分结果Table 1 Partition results for 128 processors MethodLoadimba⁃lanceratioNumberofblocksSpeedupCDGS11.04762490.340.0288GS31.04716794.410.0292BPA1.09643786.910.0289Origin131.000.0293 图10 残差收敛曲线 Fig.10 Convergence curves of residual 图11 阻力系数收敛曲线 Fig.11 Convergence curves of drag coefficient 4.2 翼身组合体DLR-F6构型 为进一步验证本文剖分算法对复杂重叠网格适用性,选取德国宇航公司的DLR-F6翼身组合体[22](DLR-F6 WB)的重叠网格作为方法验证算例,考察不同剖分方式的负载平衡效果。 整套重叠网格由3个部分组成,包括机身网格、机翼网格及背景网格,并且每个部分由多块结构网格构成。图12为DLR-F6机翼与机身网格重叠关系示意。原始网格总单元数约为1 700万,包含19个子块,且各子块网格量分布如图13所示,其中最大子块网格量约为314万。 图14为5种负载平衡方法在不同进程数下的剖分结果。图14(a)纵轴坐标为负载不均衡率,可见,除BPA外,其余4种方法均获得了满足负载平衡要求的剖分结果。而图14(b)给出了子块总数的变化曲线,可明显看出:子块分裂方法及整体型剖分方式皆影响显著,随进程数增加,GS3-int方法能极大地减少网格块数。而BPA虽然具有与GS3-sep方法类似表现,但其负载不均衡率难以满足剖分要求。 图14(c)为边界面单元数随进程数变化曲线,与网格子块数趋势类似,且GS3-int方法的边界面单元数明显少于其余4种方法。图14(d)则为进程间通信界面单元总数变化曲线,可以看到,两种整体型剖分方法表现一致,且明显优于独立型剖分方法及传统装箱算法。由此可见,剖分方式是影响该量的主导因素,而采用整体型剖分方法能够更有效地降低进程间通信成本及内存需求。 图12 DLR-F6机翼与机身构型网格重叠 Fig.12 Overset grid for DLR-F6 wing and body configuration 图13 DLR-F6 WB构型网格量分布 Fig.13 Distribution of number of grid points of DLR-F6 WB configuration 图14 DLR-F6 WB构型不同进程数时网格剖分结果 Fig.14 Partitioning properties as a function of processors for DLR-F6 WB configuration grids 为直观地说明本文4种新方法的剖分思路,图15给出了进程数为128时,不同方法所得网格子块网格量分布情况,图中横轴为单个子块网格量与平均负载网格量之比,按比值范围归为4类,纵轴为各类子块数占全部子块数的比重。从图中看出,为实现负载均衡,GS1类方法剖分出大量小网格量子块,而GS3-sep方法则保留了更多中等网格量子块。形成鲜明对比的是,GS3-int方法通过对全部子块进行筛选分裂,保留了多数满足平均负载网格量的大网格量子块,并分裂未满足要求的其余子块,以实现较少块数下的负载均衡。 图15 各子块网格量比重分布 Fig.15 Proportion for subgrids distribution of different sizes 本文提出了一种改进的多层次图剖分的多块结构网格负载平衡方法。该方法设计了新的剖分算法,采用网格子块分割与图剖分的循环调用思想,在逐步细化过程中实现负载平衡及通信量优化,同时改进了子块分裂方法,避免了子块数目过多的缺陷,并通过建立不同物体间重叠边界关联,将其拓展至多块结构重叠网格。 1) 该方法剖分过程无需人工干预,与网格拓扑无关,适用于复杂问题的多块结构网格。 2) 基于图剖分的循环调用算法能够很好地实现负载均衡及通信成本优化,提高并行效率。 3) 子块分裂方法对剖分结果影响显著,改进的子块分裂方法能够极大地减少网格块数及由内边界虚网格所带来的内存需求。 4) 对于多块结构重叠网格,采用整体型剖分方法能够有效降低进程间通信成本,显著减少网格块数及内边界面单元数。 基于现有的工作,下一步考虑将该方法发展并应用于复杂多体分离等数值模拟的并行计算。 [1] CHIEN Y P, CARPENTER F, ECER A, et al. Load-balancing for parallel computation of fluid dynamics problems[J]. Computer Methods in Applied Mechanics & Engineering, 1995, 120(1-2): 119-130. [2] RANTAKOKKO J. A framework for partitioning structured grids with inhomogeneous workload[J]. Parallel Algorithms and Applications, 1998, 13(2): 135-151. [3] MILLER G L, TENG S H, VAVASIS S A. A unified geometric approach to graph separators[C]//Proceedings of 32nd Annual Symposium of Foundations of Computer Science. Piscataway, NJ: IEEE Press, 1991: 538-547. [4] SIMON H. Partitioning unstructured problems for parallel processing[J]. Computing Systems in Engineering, 1991, 11(4): 135-148. [5] KARYPIS G, KUMAR V. METIS: Unstructured graph partitioning and sparse matrix ordering system, Technical Report[R]. Minneapolis: University of Minnesota, 1995. [6] BOMAN E G, ÇATALYÜREK U V, CHEVALIER C, et al. The Zoltan and Isorropia parallel toolkits for combinatorial scientific computing: Partitioning, ordering and coloring[J]. Scientific Programming, 2012, 20(2): 129-150. [7] YTTERSTRÖM A. A tool for partitioning structured multiblock meshes for parallel computational mechanics[J]. International Journal of High Performance Computing Applications, 1997, 11(4): 336-343. [8] RANTAKOKKO J. Partitioning strategies for structured multiblock grids[J]. Parallel Computing, 2000, 26(12): 1661-1680. [9] AHUSBORDE E, GLOCKNER S. A 2D block-structured mesh partitioner for accurate flow simulations on non-rectangular geometries[J]. Computers & Fluids, 2011, 43(1): 2-13. [10] DJOMEHRI M J, BISWAS R. Performance enhancement strategies for multi-block overset grid CFD applications[J]. Parallel Computing, 2003, 29(11-12): 1791-1810. [11] 司海青, 王同光. 多块并行计算中负载平衡策略及时间成本估算方法[J]. 航空学报, 2007, 28(S1): 57-61. SI H Q, WANG T G. Load balancing strategy for parallel calculation and time cost estimation[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(S1): 57-61 (in Chinese). [12] 李桂波, 杨国伟. 基于多块结构网格的并行计算及负载平衡研究[J]. 宇航学报, 2011, 32(6): 1224-1230. LI G B, YANG G W. Study on parallel computation and load balance strategy based on multiblock structured grid[J]. Journal of Astronautics, 2011, 32(6): 1224-1230 (in Chinese). [13] 许正, 李津, 朱自强. 网络连接机群上CFD计算的一种负载平衡方法[J]. 航空学报, 2005, 26(2):129-134. XU Z, LI J, ZHU Z Q. Load balancing strategy for parallel CFD calculation on cluster[J]. Acta Aeronautica et Astronautica Sinica, 2005, 26(2):129-134 (in Chinese). [14] BARNARD S T, SIMON H D. Fast multilevel implementation of recursive spectral bisection for partitioning unstructured problems[J]. Concurrency Practice & Experience, 1994, 6(6): 101-117. [15] KARYPIS G, KUMAR V. A fast and high quality multi-level scheme for partitioning irregular graphs[J]. SIAM Journal on Scientific Computing, 2006, 20(1): 359-392. [16] KIRICHENKO A V, MASON K, STRAUME M, et al. An efficient K-way graph partitioning algorithm for task allocation in parallel computing systems[C]//Proceedings of the First International Conference on Systems Integration. Piscataway, NJ: IEEE Press, 1990: 748-751. [17] GOURDAIN N, GICQUEL L, MONTAGNAC M, et al. High performance parallel computing of flows in complex geometries: I. Methods[J]. Computational Science & Discovery, 2009, 339(1): 104-124. [18] PELLEGRINI F. Graph partitioning based methods and tools for scientific computing[J]. Parallel Computing, 1997, 23(1-2): 153-164. [19] 刘巍, 张理论, 王勇献, 等. 计算空气动力学并行编程基础[M]. 北京: 国防工业出版社, 2013: 250-255. LIU W, ZHANG L L, WANG Y X, et al. Foundations of computational aerodynamics parallel programming[M]. Beijing: National Defense Industry Press, 2013: 250-255 (in Chinese). [20] DJOMEHRI M J, BISWAS R, LOPEZ-BENITEZ N. Load balancing strategies for multi-block overset grid applications[C]//Proceedings of the ISCA 18th International Conference Computers and Their Applications, 2003:63-71. [21] COOK P, MCDONALD M, FIRMIN M. Airfoil REA2822 pressure distributions, and boundary layer and wake measurements, experimental data base for counter program assessment: AGARD Report AR 138[R]. Paris: AGARD, 1979. [22] 2nd AIAA CFD Drag Prediction Workshop. [2016-06-27]. http://aaac.larc.nasa.gov/ts-ab/cfdlarc-dpw/June 2003. (责任编辑: 李明敏) URL:www.cnki.net/kcms/detail/11.1929.V.20160812.1059.004.html Loadbalancestrategybasedongraphpartitionformultiblockstructuredgrids LIUHongkang,YANChao*,LINBoxi,ZHAOYatian SchoolofAeronauticScienceandEngineering,BeihangUniversity,Beijing100083,China Loadbalanceisofsignificancetotheperformanceofparallelcomputing.Aimingatagoodloadbalancewithaslessblocksaspossibleinparallelcomputing,anenhancedpartitioningstrategybasedonmultilevelgraphpartitionisproposedformultiblockstructuredgrids,includingarecursivepartitionalgorithmandanimprovedsubgrid-splittingmethod,andthenextendedtotheoverlappingmultiblockgridsbyestablishingtheconnectionbetweensubgridsofdifferentbodieshereafter.Twotypicalapplications,coveringthe1to1coincidentgridandtheoverlappinggrid,areimplementedtocomparethebehaviorsofvariouspartitionstrategies,asregardsloadbalance,edge-cutandblocknumbers.Resultsdemonstratethatthesubgrid-splittingmethodiscriticaltostructuredgrids,andpartitioningover-lappinggridintegrallyisobviouslyabetteralternative.Specifically,thenewpartitioningstrategyshowsagoodperformanceinloadbalanceandcommunicationoverheads,andmeanwhiledecreasestheamountofblocksenormouslyaswellasthememoryrequirementcausedbytheghostcellofedge-cuts,leadingtoabetterparallelefficiency.Theenhancedpartitionstrategyisapplicabletoboththe1to1coincidentgridsandoverlappinggrids. computationalfluiddynamics;parallelcomputing;structuredgrids;loadbalance;graphpartition 2016-06-27;Revised2016-07-25;Accepted2016-08-08;Publishedonline2016-08-121059 .E-mailyanchao@buaa.edu.cn 2016-06-27;退修日期2016-07-25;录用日期2016-08-08; < class="emphasis_bold">网络出版时间 时间:2016-08-121059 www.cnki.net/kcms/detail/11.1929.V.20160812.1059.004.html .E-mailyanchao@buaa.edu.cn 刘宏康, 阎超, 林博希, 等. 基于图剖分的多块结构网格负载平衡方法J. 航空学报,2017,38(5):120558.LIUHK,YANC,LINBX,etal.LoadbalancestrategybasedongraphpartitionformultiblockstructuredgridsJ.ActaAeronauticaetAstronauticaSinica,2017,38(5):120558. http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn 10.7527/S1000-6893.2016.0230 V211.3 A 1000-6893(2017)05-120558-10
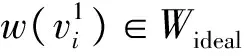
4 算例及结果分析








5 结 论
