基于最小二乘法的固定脉冲重复间隔精确估计方法

王 聪，宋新超，王星宇

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225001)

基于最小二乘法的固定脉冲重复间隔精确估计方法

王 聪，宋新超，王星宇

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225001)

在雷达信号侦察中，固定重复间隔精确估计对雷达对抗重频跟踪、雷达型号识别、雷达个体识别都具有非常重要的意义。最小二乘法具有计算量小、估计精度高、易于嵌入式实现等优点。最小二乘法对固定重复周期进行估计具有实际的应用价值。

雷达侦察；最小二乘法；脉冲重复间隔

0 引 言

在雷达参数估计中，雷达辐射源重复间隔参数是一个非常重要的参数，它决定了雷达的作用距离,还可以根据雷达的重复间隔参数来判断雷达的威胁等级。一般来说高重复频率的雷达信号具有较高的威胁等级，因此，高重复频率的信号在信号处理的过程中会被优先处理，并判断出其威胁等级，引导干扰机进行干扰。在对目标进行干扰时，如果估计出来的重复间隔精度不高，则会导致重频跟踪产生偏差，造成干扰效能下降。而当前雷达系统在设计时，都使用了高精度的时钟基准作为其信号调制脉冲源。即使如此，不同的时钟基准也存在着初始误差，只要能够得到高精度的重频间隔估计，就能够区分出不同的雷达辐射源。因此，雷达辐射源高精度重复间隔的估计能够应用到特定发射机识别(SEI)系统中。

1 最小二乘估计算法[1]

考虑超定方程组(超定指未知数小于方程个数)：

(1)

式中：i=1,2,3,…,m，m代表有m个不等式；j=1,2,3,…,n,n代表有n个未知数β；m>n。

将其进行向量化后为[2]：

Xβ=y

(2)

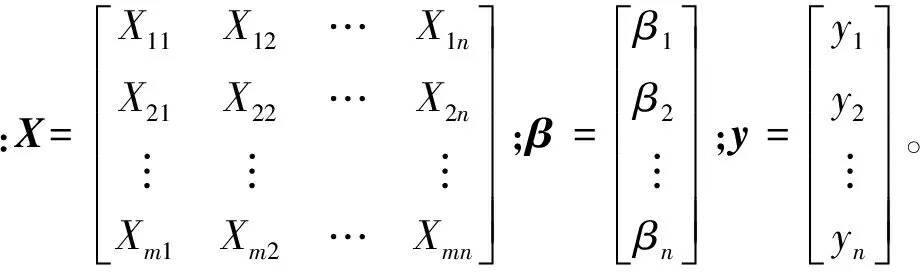
显然,该方程组一般而言没有解，所以为了选取最适合的β让等式尽量成立，引入残差平方和函数S：

S(β)=‖Xβ-y‖2

(3)

在统计学中，残差平方和函数可以看成n倍的均方根误差(MSE)。

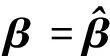
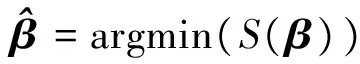
(4)

通过对S(β)进行微分求最值，可以得到：

(5)

如果矩阵XTX非奇异，则β具有唯一解：

(6)

2 最小二乘估计算法在PRI估计中的应用

在接收机对雷达脉冲信号进行测量时，会给出雷达信号的到达时间(TOA)。信号分选会对雷达脉冲信号进行去交错,得到具有固定重复间隔的雷达信号。其TOA可以建模如下：

tTOA(n)=tTOA0+ntPRI

(7)

将其化成矩阵形式为：

tTOA=Bφ

(8)

最小二乘估计的准则为：

(9)

可以得到φ的最小二乘估计为:

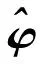
(10)

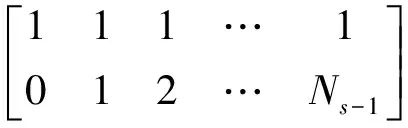
而矩阵B已知，所以可以计算出BTB：

BTB=

(11)

求其逆矩阵可得：

(BTB)-1=

(12)

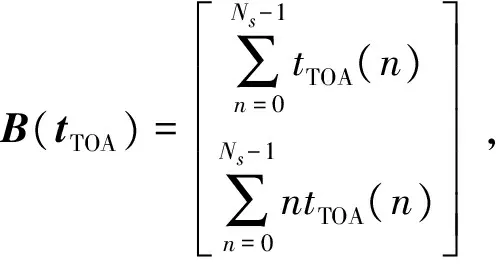
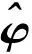
(13)

所以tPRI的最小二乘估计为：

(14)

由此得到固定重复间隔雷达tPRI的最小二乘估计值。只需要知道其tTOA就可以进行高精度重复频率估计。

3 实验结果

假定一个雷达信号具有固定重复频率，其脉冲重复间隔(PRI)为100.123,单位为μs，而截获到的脉冲数分别为100个、200个、400个和800个。所加的噪声干扰为高斯白噪声。每次都进行200次蒙特卡洛实验。实验结果如图1所示。

从图1可以看出，雷达脉冲截获得越多，最后估计出的脉冲间隔误差越小。因此，在进行雷达重复间隔估计时，积累的脉冲越多，估计的效果越好。在实际的TOA测量时，由于脉冲能量的起伏，短时间内的脉冲TOA误差不服从高斯白噪声特性。只有累计到一定量脉冲之后，脉冲TOA误差才会服从高斯白噪声分布。因此，在实际估计时，需要累计超过3个扫描周期的信号，才能获得较高精度重复间隔估计。

4 结束语

本文利用最小二乘算法对固定重复间隔的雷达信号进行重复间隔估计。该方法具有计算量小、易于嵌入式实现等优点，能够应用到雷达参数估计、重频跟踪、型号识别、个体识别系统中去。该方法还能用于估计参差信号的骨架间隔等参数，但是对于抖动信号的重复间隔估计无效。针对抖动信号的重复间隔估计还需要开发其它的算法。

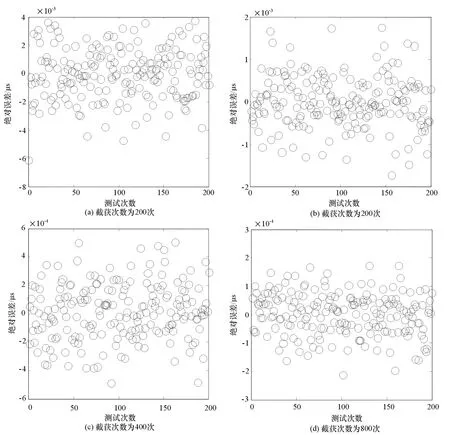
图1 利用最小二乘估计算法估计的重复间隔误差

[1] 王鼎.无源定位中的广义最小二乘估计理论与方法[M].北京：科学出版社,2015.

[2] 龚李铱.利用频率变化率和波达角变化率单站无源定位与跟踪的关键技术研究[D].长沙：国防科技大学，2004.

[3] 叶其寿，沈永欢.实用数学手册[M].2版.北京：科学出版社，2009.

AccurateEstimationMethodforFixedPRIBasedonLeastSquareMethod

WANG Cong,SONG Xin-chao,WANG Xing-yu

(The 723 Institute of CSIC,Yangzhou 225001,China)

In radar signal reconnaissance,the accurate estimation of fixed pulse repetition interval (PRI) is of important meaning for repetition frequency tracking，radar type identification and radar individual identification in radar countermeasure.Least square method has the characteristics of less calculation,high estimating accuracy and being easy embedded.The least square method has the actual application value for the estimation of fixed PRI.

radar reconnaissance;least square method;pulse repetition interval

TN971.1

A

CN32-1413(2017)05-0087-03

10.16426/j.cnki.jcdzdk.2017.05.019

2017-03-02