一种快速重频参差信号分选方法

刘正成，齐永梅，姚志均

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225001)

一种快速重频参差信号分选方法

刘正成，齐永梅，姚志均

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225001)

针对重频参差信号的分选，提出了一种快速信号分选方法，首先对参差信号脉冲序列的到达时间(TOA)做一次一阶差分运算，然后提取出所有满足条件的脉冲重复间隔(PRI)值，同时得到该参差信号的相周期、帧周期和参差数；最后，对脉冲序列的TOA做一次或多次高阶差分运算，并利用之前获得的相周期和参差数，解出各相周期的顺序关系。仿真实验结果表明，本文提出的方法在脉冲丢失率达到40%时仍能正确分选，且计算速度快。

雷达信号分选；脉冲重复间隔；参差信号；差值直方图

0 引 言

雷达信号分选是电子支援措施(ESM)和电子情报(ELINT)的关键组成部分，是指从接收机截获到的密集雷达脉冲流中分离出属于各部雷达的脉冲串，其实质就是对脉冲序列进行去交叠、去交错处理。在密集的电磁信号环境中，一般利用脉冲的瞬时参数，如载频(RF)、到达方向(DOA)、脉宽(PW)和脉冲幅度(PA)等进行预分选，可以起到稀释信号密度的作用；然后利用脉冲的到达时间(TOA)进行主分选，也称重频分选，主要是通过估计各部雷达的脉冲重复间隔(PRI)，并根据PRI抽取脉冲实现分选目的。

目前雷达侦察系统中常用的基于PRI的分选算法有自相关函数法[1]、累积差值直方图法(CDIF)[2]、序列差值直方图法(SDIF)[3]和PRI变换法[4-5]。Mardia等人[2]对PRI分选进行了深入研究，在传统直方图分析方法的基础上结合序列检索算法，提出了累积差直方图算法，该算法对于干扰脉冲和脉冲丢失不敏感，但当PRI具有随机抖动变化时，无法正确分选，而且CDIF需要计算很大的差值级数，当脉冲丢失时，会出现子谐波。之后，Milojevic等人[3]对CDIF算法进行改进，提出了序列差直方图算法，解决了CDIF算法中计算量大的问题，取消了2倍脉冲间隔的直方图值与门限比较，从而节约了一半时间，但SDIF法仍然存在与CDIF法一样致命的缺点，即当PRI具有随机抖动特征时，无法正确分选，且无法抑制谐波的出现。为此，Nelson等人[4]提出了PRI变换法，该方法在计算自相关时增加了一个相位因子以抑制子谐波，随后Nishiguchi等人[5]对PRI变换法做了改进，采用可变的时间起点和交叠的PRI箱技术以解决因抖动引起的相位误差增大问题，从而实现对重频抖动信号的分选。

CDIF、SDIF、PRI变换这3种方法都是针对重频固定或重频抖动的雷达信号的，当用于重频参差信号分选时，理想情况下，即没有脉冲丢失时，根据脉冲序列的到达时间进行一级差值直方图计算，然后对直方图结果进行统计，统计峰值个数，将各峰值之间的差值在规定的容差范围内的值提取出来，进行地址对确认，还能正确分选，但当脉冲密度大、参差数多、脉冲丢失率高的情况下，它们就失效了。为此，本文提出了一种在脉冲丢失率很高时仍能正确分选的新方法，且该方法没有参数需要设置，计算量小。

1 重频参差信号的脉冲序列模型

重频参差信号的数学模型[6]如下：

(1)

图1给出了一个6参差的重频参差脉冲序列示意图。重频参差信号具有一定的反侦察能力，因为具有不同的重频，使得在距离和速度上不易产生模糊。通常情况下，最大参差比被限制在1.5～2.0之间[7]，也就是说最大相周期不大于2倍的最小相周期。

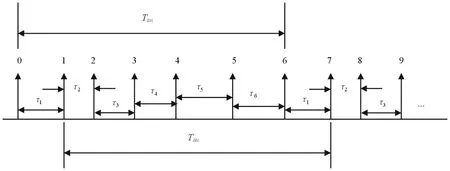
图1 参差信号PRI

2 本文提出的信号分选新方法

上一节已提到，一般情况下参差信号的最大参差比不超过2，根据这一约束条件，本文提出了一种快速重频参差信号分选新方法。本方法主要分两大步：第1步，利用TOA信息估计帧周期、相周期及参差数；第2步，解算各相周期之间的顺序关系。新方法的详细步骤如下：

(1) 对于一个含有N个脉冲的参差脉冲序列，对其到达时间tTOA(i)，i=0,1,…,N-1做一次一阶差分运算，得到一个关于PRI信息的向量D1，其计算公式为：

D1(i)=tTOA(i+1)-tTOA(i),0≤i≤N-2

(2)

(3)

(4)

(3) 对脉冲序列的TOA做一次M阶差分运算，得到向量DM，然后判断向量DM中是否有等于帧周期Tau的值。若有，任选一个值为帧周期的索引号i，并对从i到i+M的TOA做一次一阶差分运算，得到各相周期之间的顺序关系：τ1,τ2,…,τM；若没有，则令m=M-1，并转(4)。

(4) 对脉冲序列的TOA做一次m阶差分运算，得到向量Dm，然后判断向量Dm中是否有等于帧周期Tau的值。若有，设向量Dm中共有l个元素的值等于帧周期Tau，它们的索引号向量Ind为:

Ind={i|Dm(i)=Tau}

(5)

(5) 根据这些索引号从TOA中提取数据，得到一个l×(m+1)维矩阵C，其每一行元素为：

C(j,:)=tTOA(Ind(j):Ind(j)+m)

(6)

(6) 对矩阵C中的每一行做一次差分运算，得到的仍是一个矩阵，然后该矩阵中可能存在元素相同的行，故对其做去重复处理，最终得到一个r×m维矩阵T。

(7) 因为存在脉冲丢失，故矩阵T往往存在多行数据，即有r>1，此时可以结合估计得到的{τq}q∈{1,…,M}解出各相周期的顺序关系：τ1,τ2,…,τM；若此时的矩阵T只有一行，即r=1，则令m=m-1，并重复步骤(4)～(7)，直至解出各相周期的顺序关系为止。

3 仿真验证

3.1 有效性验证

图2 无脉冲丢失情况下的参差脉冲序列各参差时序图

图3 有脉冲丢失情况下实际检测到的各脉冲PRI值

图4 将图3中的脉冲对应到图2中的效果图

图5 对参差脉冲序列的TOA做一次一阶差分运算所得的向量

获得相周期和参差数后，接下来就解算各相周期之间的顺序关系。图6是对脉冲序列的TOA做一次6阶差分运算后得到的向量D6。从图6中可以看出,没有一个元素的值是等于407的，于是对脉冲序列的TOA做一次5阶差分运算后得到向量D5，如图7所示。从图7可以看出，有3个元素的值是等于407的，它们的索引号分别为11、12和14，然后根据步骤(5)和(6)得到关于相周期顺序关系信息的矩阵T，如图8所示。图8表示1个帧周期内脉冲数为5个，即表示5个相周期，实际估计得到的相周期个数为6个，它们的集合EstimatedTAU为：{50,53,56,77,79,92}。取矩阵T中的第1行，并与估计得到的参差集合EstimatedTAU作比较，发现第1行中多了一个“148”，但少了2个值：“92”和“56”。可以发现，第1行中多出来的这个“148”刚好等于少的这2个PRI值之和，于是可以肯定“56”和“92”应该位于“148”这个位置，至于两者的前后关系待定，而其他4个相周期的顺序关系已定。接着观察矩阵T的第2行，看该行中是否出现“56”或“92”，只要出现其中一个，则它们两者的顺序就可以确定下来，而事实上该行中出现了“92”，而“92”之前的值为“77”，故“56”应该在“92”之后，于是该脉冲序列各相周期的顺序关系为：77、92、56、79、50、53，与实际的顺序关系一致。

图6 对脉冲序列的TOA做一次6阶差分运算后得到的向量D6

图7 对脉冲序列的TOA做一次5阶差分运算后得到的向量D5

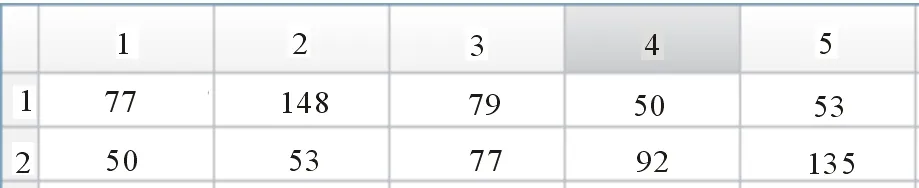
图8 根据步骤(5)和(6)所得的矩阵T

3.2 快速性验证

为了验证本文方法的快速性，进行本文方法与CDIF算法的计算耗时对比试验，即针对不同参差数的参差信号，比较2种方法的耗时。参差信号的参差数取值范围为4～8，对于每一种参差数，都测试50次，然后取平均值，统计结果如表1。注，在脉冲丢失率高时，CIDF算法无法解算各相周期之间的顺序关系，故这里CDIF算法的耗时只算它正确估计出帧周期所耗的时间，而本文方法的耗时是指估计出正确的帧周期、相周期、参差数及各相周期之间的顺序关系所耗时间。从表1可以看出，本文方法比CDIF算法快。

4 结束语

当重频参差信号脉冲序列中的脉冲丢失率比较高时，传统的基于PRI的CDIF或SDIF最多只能估计出帧周期和参差数，但无法解算各相周期及它们之间的顺序关系。为此，本文提出了一种快速信号分选方法。该方法首先对TOA进行一级差值计算，然后根据参差比约束条件得到相周期、参差数和帧周期，接着再对TOA进行多级差值计算，并结合已获得的相周期和参差数解算出各相周期的顺序关系。实验结果表明，在脉冲丢失率高达40%的情况下，本文方法仍能正确估计出帧周期、参差数、相周期及它们之间的顺序关系；此外，与CDIF相比，计算耗时小很多(如表1所示)，且无需设置任何参数。

表1 本文方法与CDIF算法计算耗时对比(单位：s)

[1] 赵健生.舰载干扰机信号分选的分类处理方法[J].船舶工程，1995(2):45-49．

[2] MARDIA H K.New techniques for the deinterleaving of repetitive sequences[J].IEEE Proceedings,1989,136(4):149-154.

[3] ILOJEVIC D J,POPOVIC B M.Improved algorgithm for the deinterleaving of radar pulse[J].IEEE Proceeding,1992,139(1)：98-104.

[4] NELSON D J.Special purpose correlation functions for improved signal detection and prameter estimation[C]//Proceedings of International Conference on Acoustics,Speech,and Signal Processing (ICASSP),1993:73-76.

[5] KENICHI N,MASACKI K.Improved algorithm for estimating pulse repetition intervals[J].IEEE Transactions on Aerospace and Electronic Systems,2000,36(2):407-421.

[6] 赵国庆.雷达对抗原理[M].西安:西安电子科技大学出版社,1999.

[7] 丁鹭飞,耿富录.雷达原理(修订版)[M].西安:西安电子科技大学出版社,1980.

SortingMethodofAFastPRFStaggeredSignal

LIU Zheng-cheng,QI Yong-mei,YAO Zhi-jun

(The 723 Institute of CSIC,Yangzhou 225001,China)

This paper proposes a fast signal sorting method for the sorting of pulse reqetition interval (PRF) staggered signal,firstly uses the proposed method to calculate the first-order differential values of the time of arrival (TOA) for staggered signal pulse sequence;then extracts all PRI values to meet the conditions;obtains the phase cycle,frame period and the number of stagger PRIs of the staggered signal;finally makes one or more high order differential operations on the TOA of staggered pulse signal sequence,and solves the order relationship of all phase cycles by using the obtained phase cycles and the number of stagger PRIs.The simulation results show that the proposed method still correctly sort the staggered signal sequence when the pulse loss rate reaches 40%,and the computing speed is fast.

radar signal sorting;pulse repetition interval;stagger signal;difference histogram

TN971.1

A

CN32-1413(2017)05-0070-04

10.16426/j.cnki.jcdzdk.2017.05.015

2017-08-30