亚临界圆柱绕流的DES方法比较

唐虎， 常士楠,*， 成竹， 马兰

1.北京航空航天大学 航空科学与工程学院， 北京 100083 2.中国飞机强度研究所， 西安 710065

亚临界圆柱绕流的DES方法比较

唐虎1， 常士楠1,*， 成竹2， 马兰2

1.北京航空航天大学 航空科学与工程学院， 北京 100083 2.中国飞机强度研究所， 西安 710065

针对地面结冰试验设施喷雾系统尾迹湍流模拟需求，考察了3种脱体涡模拟(DES)方法对三维亚临界圆柱绕流预测的准确性，比较和分析了瞬时流动特征和流场统计量。研究发现：1) 从瞬时流动特征来看，k-ω雷诺平均Navier-Stokes(RANS)控制的区域对剪切应力输运k-ωDES (SSTk-ωDES)求解的准确性有显著影响；2) 从流动参数统计量的误差范围来看，回流区长度和流向最小速度的预测质量能在一定程度上反应圆柱绕流数值模拟的准确性；3) 综合比较，SSTk-ωDES预测值与试验值和大涡模拟(LES)数据最为吻合，具有应用于地面结冰试验设施喷雾系统尾迹湍流计算的潜力。

湍流扩散； 尾迹流动； 脱体涡模拟； 涡结构； 统计量

地面结冰试验设施由于具备可控的结冰云雾模拟能力而在飞机结冰研究和冰防护系统发展过程中发挥重要作用，而液态水含量均匀性作为地面结冰试验设施的一个重要设计指标，是设计阶段必须要考虑的。此前的研究[1-7]已经表明地面结冰试验设施喷雾棒尾迹湍流对水滴扩散有显著影响。要正确地预测尾迹湍流对水滴的扩散行为，就必须合适地捕捉喷雾棒尾迹湍流。

气流绕喷雾棒流动属于亚临界钝体绕流，涉及边界层分离、剪切层发展、非定常涡的产生与脱落、涡与涡之间相互作用等复杂物理现象。脱体涡模拟(Detached Eddy Simulation,DES)是一种致力于解决三维非定常大分离流动的湍流求解方法[8]，最早由Spalart等[9]提出，该方法在网格分辨率适用于大涡模拟(Large Eddy Simulation，LES)的区域发挥类似于LES亚格子尺度模型的作用，而在网格分辨率不适用于LES的区域发挥雷诺平均Navier-Stokes(Reynolds Averaged Navier-Stokes，RANS)模型的作用[10]，这样可在保证计算精度可接受的同时较大幅度地节省计算资源。

DES方法经过逐步改进[11-19]，已成功应用于多项实际工程中[20-32]。目前构建的较为常用的DES方法有Spalart-Allmaras DES(S-A DES)[33]方法、Realizablek-εDES(Rk-εDES)[34]方法和剪切应力输运k-ωDES(SSTk-ωDES)[35]方法(k为湍动能；ε为耗散率；ω为比耗散率)。在DES方法比较研究方面，Strelets[8]在将S-A DES推广至SSTk-ωDES时以ReD=50 000(ReD为圆柱雷诺数)圆柱绕流案例进行了模型测试，比较了瞬时涡量、阻力系数、升力系数、雷诺应力和圆柱表面压力系数分布，但仅有压力系数分布与试验数据进行了比较。Nichols[36]则以ReD=8×106圆柱绕流案例对S-A DES、SSTk-ωDES和SST多尺度模型进行了比较，分析了计算结果对时间步长和网格分辨率的敏感性，认为采用隐式算法时需要对每个涡脱落周期捕捉至少200步，但Nichols[36]仅对阻力系数CD和斯特罗哈尔数St与试验数据进行了比较，没有对这3种方法预测的流动统计量以及瞬时流动特征与试验进行全面比较，因此难以说明哪种方法更适用于亚临界流动。

作为喷雾棒尾迹湍流对水滴的扩散研究的第1步，本研究拟采用上述3种DES方法对亚临界圆柱绕流进行计算，并将预测的瞬时流动特征和流动统计量与可用的试验数据进行比较与分析，确定可准确描述亚临界钝体尾迹湍流特征的DES方法，为下一步不同喷雾棒外流场数值计算和水滴扩散计算奠定基础。

1 数值方法

1.1 控制方程

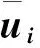
(1)

将这种形式的速度表达式代入瞬态连续性方程和动量方程，并取时间平均可得到

(2)

式中：ρ为密度；t为时间。

(3)

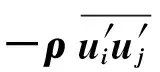
湍流建模的RANS方法要求式(3)中的雷诺应力适当模化。一般采用Boussinesq假设将雷诺应力与平均速度梯度联系起来，即

(4)

式中：μt为湍流黏性。

下面给出本文考察的3种雷诺应力模化DES方法。

1) S -A DES

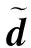
(5)

式中：CDES,S -A为S-A DES的模型常数，取值为0.65；Δmax为网格在x、y或z方向的最大值，即

Δmax=max(Δx,Δy,Δz)

(6)

2) Rk-εDES

在Rk-εDES模型中，耗散项Yk由式(7)修正。

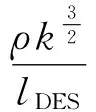
(7)

式中：lDES为DES模型湍流长度，其表达式为

lDES=min(lRk ε,lLES)

(8)

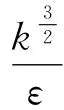
(9)

lLES=CDES,Rk εΔmax

(10)

其中：lRk ε和lLES分别为Rk-εRANS模型和LES模型湍流长度；CDES,Rk ε为Rk-εDES的模型常数，取值为0.61。

3) SSTk-ωDES

采用式(11)对SSTk-ωDES模型中的湍动能耗散项Yk进行修正。

Yk=ρβ*kωFDES

(11)

式中：β*为修正系数；FDES的表达式为

(12)

其中：CDES,SST为SSTk-ωDES的模型常数，取值为0.61；Lt为湍流长度尺度，在RANS中的定义为

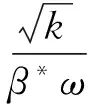
(13)

1.2 求解方法

采用ANSYS 14.5 Fluent软件平台开展数值计算。由于研究的流动为低速不可压缩非定常流动，因此选用基于压力的求解器进行瞬态模拟，并采用压力隐式分裂算子(Pressure-Implicit with Splitting of Operators，PISO)进行压力-速度耦合求解。对于瞬态模拟，控制方程必须在空间和时间上进行离散。在空间离散上，连续性方程采用有限差分方法，并采用算术平均处理密度插值；动量方程采用有界中心差分格式(Bounded Central Differencing Scheme)进行离散，其压力梯度项采用基于单元的最小平方法进行计算，压力项采用动量方程系数处理表面处的压力差值；湍动能和耗散率采用二阶迎风格式。在时间离散上，采用二阶隐式格式。

2 结果与讨论

2.1 计算域、网格与边界条件

选用具有代表性的ReD=3 900亚临界圆柱绕流进行模型测试，因为这种流动有Lourenco和Shih[37]、Norberg[37](报道于文献[37]中)、Ong和Wallace[38]、Parnaudeau等[39]的试验数据用于比较，而且这些试验数据也被广泛地用于模型测试。本文主要采用Parnaudeau等[39]在2008年采用热线风速仪(Hot Wire Anemometry, HWA)和粒子图像测速(Particle Image Velocimetry,PIV)获取的ReD=3 900圆柱绕流试验数据进行模型验证，另外还引用了Parnaudeau等[39]在相同条件下的LES数据进行比较。文献[39]中圆柱直径D=12 mm，长径比L/D=24，空气密度ρ=1.205 kg/m3，空气温度ta=20 ℃，空气动力黏性系数μa=1.81×10-5Pa·s，来流空气速度Uc=4.8 m/s。

参照文献[37]中的圆柱绕流计算域选取经验，确定计算域为：流向-15≤x/D≤15，侧向-15≤y/D≤15，展向-2≤z/D≤2，圆柱体中心位于x/D=0的位置，如图 1(a)所示。在网格设计时，要考虑圆柱边界层长度尺度、分离剪切层和涡结构。Spalart[40]和Bunge等[41]对DES方法的使用、网格系统和网格尺寸(Δx,Δy,Δz)设计给出了建议。此处参考Travin等[42]开展圆柱绕流DES计算时的网格系统设计方法，将流体计算域分为3块，即RANS域、LES域和欧拉域，3个域的交点A由剪切层长度确定，约为(1.09,1.03)，如图1(b)所示。

为了准确地描述边界层的发展与脱落，RANS域第1层网格厚度Δy取0.003D，对应的y+≈1，y方向网格增长率取1.15，这样可保证边界层内(以0.99Uc确定)分布有足够的节点。这样得到RANS域在交点A处的Δy约为0.045D，考虑到DES方法要求LES域具有近似的各向同性网格，因此RANS域第1层网格Δx取0.015D，这样可以保证交点A处的Δx≈Δy。展向网格分辨率要考虑涡结构尺度，根据Mansy[43]和Williamson[44]等的试验研究，在近圆柱尾迹区域的展向波长尺度约为

(14)

根据式(14)，ReD=3 900时的展向波长λz/D≈0.4，故第1层网格展向取Δz=0.05D可保证每个波长内分布约8个节点。因此整个网格系统节点分布：RANS域为195×65×85，LES域为 46×151×85，欧拉域为75×51×85，总网格数约为200万。

根据Parnaudeau等[39]的试验条件，设置计算的入口速度Uc=4.8 m/s，入口湍流强度为0.2%，圆柱表面为无滑移静止壁面，展向方向设置为对称边界。为了保证方程求解满足CFL(Courant-Fredrichs-Levy)限制条件，取固定时间步长Δt=0.02D/Uc进行计算，这样可使每个涡脱落周期捕捉约240次，满足文献[36]提到的时间步长要求。

2.2 瞬时流动特征

在对DES模拟数据进行处理时，发现Rk-εDES给出的预测数据具有显著的RANS特征，为了表明Rk-εDES结果的可靠性，此处同时引入Rk-εRANS结果进行比较。图2和图3 分别给出了瞬态展向涡分量ΩzD/Uc和侧向涡分量ΩyD/Uc在2个对称面(z=0和y=0)上的分布，为了与Parnaudeau等[39]的PIV试验数据和LES数据进行比较，此处坐标轴与涡量范围的选取均与Parnaudeau等[39]的一致。从图2 可看出，在z=0平面，S-A DES和SSTk-ωDES在圆柱两侧均预测出两条细长的剪切层，且剪切层几乎一直延伸到x/D=2，这与试验测量以及LES结果较为吻合，然而Rk-εDES却预测出了两条相对粗短的剪切区域，没能预测出明显的剪切层特征。在尾迹区内，3种DES方法给出了尺度较为接近的涡结构，这是因为DES在该区域内转换为LES，但受上游解析能力的影响，DES在尾迹区内的微小尺度涡结构预测能力稍弱于LES。Rk-εRANS预测出的边界层和剪切层与Rk-εDES得到的结果极为相似，而Rk-εDES有在近壁区保持为Rk-εRANS的特点，这也表明Rk-εDES的预测结果是可靠的。另外，Rk-εRANS在尾迹区几乎没能捕捉到展向涡分量，这是由于RANS构架下产生过高的湍流黏性，使得流场的脉动信息被剧烈耗散。

从图3可看出，在y=0平面，3种DES方法均预测出了交替出现的湍流涡以及无旋区，因此3种DES方法均能预测出圆柱下游区的卡门涡街，而且预测的涡街排列与试验及LES较为接近，均与圆柱基本平行，表明了流动结构的三维特征。但3种DES方法中，Rk-εDES预测的侧向涡量ΩyD/Uc较弱。另外，Rk-εRANS几乎没能捕捉到侧向涡分量，这说明RANS在预测流动的三维特征方面表现欠佳。

文献[39]没有给出总涡量ΩD/Uc在z=0平面分布的试验数据，这里给出3种DES方法在z=0平面的瞬态涡量(ΩD/Uc取0～10)以供比较，如图4所示。从图4可见，S -A DES和SSTk-ωDES均预测出了不稳定的剪切层从圆柱表面分离，并逐步发展为周期性的卡门涡街这一过程，而Rk-εDES和Rk-εRANS对流动结构的发展过程预测能力较弱。Rk-εDES在预测下游尾迹区的涡结构能力方面与S-A DES和SSTk-ωDES相当，这也体现了DES方法在该区域保持LES特性的解析能力。Rk-εRANS预测的尾迹区涡量偏弱，这是由于RANS产生过高的湍流黏性。

从构造的角度来看，DES方法在边界层区域保持RANS，在远场转化为LES。而SSTk-ωDES中的RANS部分本身就包含了k-ωRANS和k-εRANS两部分，仅是采用混合函数进行了处理，使得SSTk-ωRANS在边界层近壁区保持为k-ωRANS，在边界层远壁区切换为k-εRANS，以发挥出更好的性能[45]。Strelets[8]认为影响SSTk-ωDES准确性的主要是k-εRANS控制的区域。本文给出的Rk-εDES和SSTk-ωDES结果在边界层分离和剪切层发展区域存在较大差异，然而Rk-εDES预测的边界层分离和剪切层发展行为又与Rk-εRANS较为接近，这说明Rk-εDES在边界层区域的确是采用k-εRANS进行求解。以上分析表明k-ωRANS控制的区域对SSTk-ωDES求解的准确性也有较大影响。

从涡量数据来看，流向涡分量ΩxD/Uc和侧向涡分量ΩyD/Uc的量值相当；展向涡分量ΩzD/Uc较大，是涡量的主要分量，这进一步体现了流动的三维特征。

2.3 流动统计量

在比较流动统计量时，首先要考虑流场统计量的收敛性。很多研究者在对流场统计量进行处理时所取的平均时间都不一致，例如Kravchenko和Moin[37]用7个涡脱落周期计算流场统计量，而Dong等[46]使用40～50个涡脱落周期，Ma等[47]又采用131个涡脱离周期。Franke和Frank[48]研究了流场统计量的收敛性，认为至少需要40个涡脱离周期才能获取收敛的流动统计量。目前的数值模拟均在尾迹湍流形态规律稳定之后开始对瞬态流场进行采样。所有的统计量都是基于T=240D/Uc(约50个涡脱落周期)取平均得到，平均符号由“〈·〉”表示。

表1中给出了ReD=3 900圆柱绕流统计量。圆括号内的值表示数值计算数据与试验数据的误差，“+”表示偏大，“-”表示偏小。从表 1可以看出，3种DES方法得到的阻力系数CD均稍小于试验测量值，而LES方法得到的CD稍大于试验测量值，这说明DES方法预计的分离点比试验测量得到的分离点稍微延后，这也由DES方法计算得到的分离角θsep均大于试验测量值所证实。3种DES方法预计的阻力系数与试验最为接近的是SSTk-ωDES，误差仅为1%。-Cpb为背压系数，Cpb为圆柱基点(Base Point，θ=180°)处的压力系数。3种DES方法计算的-Cpb均比试验测量值小，精度最高的是SSTk-ωDES模型，误差为14%，精度不及LES方法(误差为7%)，这和Norberg[37]是在ReD=4 020条件下测量的-Cpb有关。此前有研究者认为，St数(St=fD/Uc，f为涡脱落频率)对网格分辨率和时间步长不敏感，笔者在网格分辨率和时间步长调试过程中也发现了这一点，但DES模型仍然对St数有轻微影响，3种DES方法中SSTk-ωDES模型预计的St数与试验最为接近，误差为1%，精度与LES相当。3种DES方法计算的分离角θsep基本相同，最接近试验值的是Rk-εDES，误差为5%。回流区长度Lrec为圆柱基点与中心线上平均流向速度〈u〉符号转变点之间的距离，如图5所示。由表1可看出，3种DES方法在回流区长度和流向最小速度umin预测方面存在较大差异，S-A DES预测的Lrec比Parnaudeau等[39]得到的试验值大39%，Rk-εDES预测的Lrec比Parnaudeau等[39]得到的试验值小50%，SSTk-ωDES预测的Lrec与Parnaudeau等[39]得到的试验值最为接近，仅偏大8%。S-A DES方法给出了较为准确的流向最小速度umin，约偏低6%。从流动参数统计量的误差范围可以看出，3种DES方法得到的流动参数CD、-Cpb、St和θsep的误差较为接近，仅回流区长度Lrec和流向最小速度umin的误差有明显差异，因此回流区长度Lrec和流向最小速度umin的预测质量能在一定程度上反应圆柱绕流数值模拟的准确性。另外，通过比较Rk-εRANS和Rk-εDES预计的流动统计量可以发现，Rk-εDES预计的流动统计量具有显著的RANS特征，这表明在Rk-εDES中k-εRANS对边界层区域表现出了过分抑制。

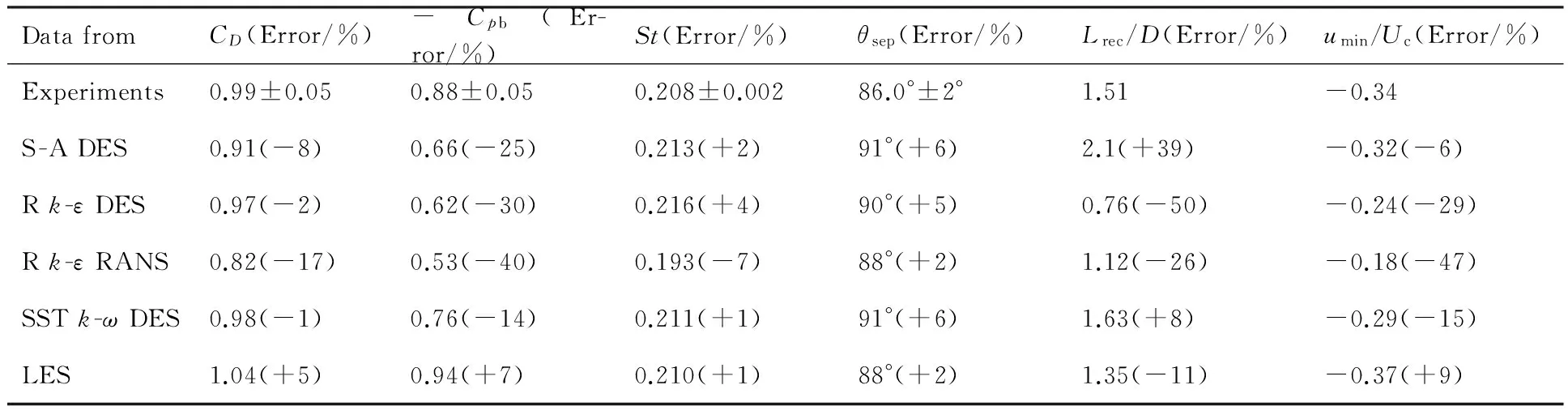
表1 ReD=3 900圆柱绕流统计量Table 1 Statistics of flow around circular cylinder at ReD=3 900

图5给出了尾迹中心线上平均流向速度〈u〉分布。虽然3种DES方法预测的〈u〉变化趋势几乎一致，均是随着尾迹中心线的延伸先逐步减小，达到最小速度umin后再增大，最后趋于平稳，但是仅有SSTk-ωDES模型得到的〈u〉在整个尾迹区(x/D≥0.5)与Parnaudeau等[39]的试验数据最为吻合(和LES数据基本一致)，而S -A DES模型和Rk-εDES模型预测的〈u〉仅在远尾迹区(约x/D≥6)与试验数据较为接近。这里引入了Lourenco和Shih[37]以及Ong和Wallace[38]的试验数据作为比较。Ong和Wallace[38]仅给出了回流区下游的〈u〉分布，Lourenco和Shih[37]给出了包含回流区的〈u〉分布。Lourenco和Shih[37]试验测量得到的Lrec比Parnaudeau等[39]测量得到的Lrec小，Kravchenko和Moin[37]认为这是由于内流干扰导致剪切层过早转捩形成的。

将3种DES方法获取的z=0平面3个不同流向位置处的平均流向速度〈u〉分布(见图6)和平均侧向速度〈v〉分布(见图7)与Parnaudeau等[39]以及Lourenco和Shih[37]的近尾迹区试验数据进行比较，并引入Parnaudeau等[39]的LES数据作为参考。为了便于与试验数据进行比较，流向位置的选取与试验一致。

总体看来，〈u〉分布呈现出明显的对称性，〈v〉分布呈现出明显的反对称性。从模拟与试验数据的接近程度来看，对于〈u〉的预测，S -A DES数据偏大，Rk-εDES数据〈u〉偏小；对于〈v〉的预测，S -A DES模拟数据又偏小，而Rk-εDES数据偏大，只有SSTk-ωDES与Parnaudeau等[39]的试验数据最为接近，与LES仅存在极小的差异。值得注意的是，在位于回流区的x/D=1.06处(见图 6(a))，S -A DES、SSTk-ωDES和LES都给出了U型轮廓的〈u〉分布，这和Parnaudeau等[39]试验给出的〈u〉分布轮廓几乎完全一致。然而Rk-εDES却给出了V型〈u〉分布，这又和Lourenco和Shih[37]试验给出的〈u〉分布轮廓接近。注意到试验和模拟数据在回流区边缘区域x/D=1.54和回流区下游x/D=2.02处都给出了V型〈u〉分布，这说明〈u〉分布可能是从回流区的U型轮廓发展为回流下游尾迹区的V型轮廓。从图7的〈v〉分布可明显看出，除Lourenco和Shih[37]的试验数据外，所有的模拟和试验数据均给出了反对称的〈v〉分布，这种异常行为也表明Lourenco和Shih[37]的试验测量可能受到某些外部干扰的影响，导致剪切层过早转捩，影响回流区尺寸和近尾迹区的速度轮廓形状，这也从图 5中Lourenco和Shih[37]试验得到的回流区长度Lrec得到证实。

图8给出了圆柱表面z=0处压力系数分布。由于Parnaudeau等[39]没有给出圆柱表面压力系数分布的试验数据，这里用Norberg[37]在ReD=4 020 下的试验数据进行比较。在DES方法中，尽管3种DES方法均给出了相同的Cp变化趋势，但S-A DES和Rk-εDES(两条线几乎完全重合)方法给出的Cp分布与试验数据偏离较远，SSTk-ωDES方法与试验数据较为接近，精度能比前两种DES方法高1倍，但仍不及LES。另外，DES方法中驻点处的压力系数略微大于1，这在Travin等[42]的圆柱绕流DES方法中也曾出现，Travin等[42]认为这种误差会随计算域的增大而减小，然而背压却对计算域的增大不敏感。研究较为关注的是背压系数，而不是驻点处的压力系数，因此在目前的计算域条件下得到的压力系数分布误差是可以接受的。

3 结 论

1) 从瞬时流动特征来看，k-ωRANS控制的区域对SSTk-ωDES求解的准确性有显著影响。

2) 从流动参数统计量的误差范围来看，回流区长度Lrec和流向最小速度umin的预测质量能在一定程度上反应圆柱绕流数值模拟的准确性。

3) 综合比较，SSTk-ωDES预测值与试验和LES数据最为吻合，具有应用于地面结冰试验设施喷雾系统尾迹湍流计算的潜力。

[1] MAREK J, OLSEN W A. Turbulent dispersion of the icing cloud from spray nozzles used in icing tunnels: NASA TM-87316[R]. Washington, D.C.: NASA, 1986.

[2] BARTLETT C S. Turbine engine icing spray bar design issues[J]. Journal of Engineering for Gas Turbines and Power, 1995, 117(3): 406-412.

[3] DEANGELIS B C, LOTH E. Simulations of turbulent droplet dispersion in wind-tunnel icing clouds[J]. Journal of Aircraft, 1997, 34(2): 213-219.

[4] HANCIR P, ANDERSON A, LOTH E. Computations of droplet distributions in the NASA icing research tunnel: AIAA-2000-0101[R]. Reston: AIAA, 2000.

[5] BHARGAVA C, LOTH E, POTAPCZUK M. Aerodynamic simulations of the NASA Glenn icing research tunnel: AIAA-2003-0566[R]. Reston: AIAA, 2003.

[6] LEE A, LOTH E. Droplet dispersion in the NASA Glenn icing research tunnel: AIAA-2010-7533[R]. Reston: AIAA, 2010.

[7] CLARK K, MALINOWSKI M, LOTH E. Air flow and liquid water concentration simulations of the 2012 NASA Glenn icing research tunnel: AIAA-2012-2936[R]. Reston: AIAA, 2012.

[8] STRELETS M. Detached eddy simulation of massively separated flows: AIAA-2001-0879[R]. Reston: AIAA, 2001.

[9] SPALART P R, JOU W H, STRELETS M, et al. Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach[C]//1st AFOSR International Conference on DNS/LES. Dayton, OH: Greyden Press, 1997: 14-18.

[10] SPALART P R. Detached-eddy simulation[J]. Annual Review of Fluid Mechanics, 2009, 41: 181-202.

[11] VATSA V N, SINGER B A. Evaluation of a second accurate Navier-Stokes code for detached eddy simulation past a circular cylinder: AIAA-2003-4085[R]. Reston: AIAA, 2003.

[12] HANSEN R P, FORSYTHE I R. Large and detached eddy simulation of flow over a circular cylinder using unstructured grids: AIAA-2003-0775[R]. Reston: AIAA, 2003.

[13] ROY C J, DECHANT L J, PAYNE J L, et al. Bluff-body flow simulations using hybrid RANS/LES: AIAA-2003-3889[R]. Reston: AIAA, 2003.

[14] LO S C, HOFFMANN K A, DIETIKER J F. Numerical investigation of high Reynolds number flow over square and circular cylinders[J]. Journal of Thermophisics and Heat Transfer, 2005, 19(1): 72-80.

[15] NISHINO T, ROBERTS G T, ZHANG X. Unsteady RANS and detached-eddy simulations of flow around a circular cylinder in ground effect[J]. Journal of Fluid and Structure, 2008, 24(1): 18-33.

[16] JEE S, SHARIFF K. Detached-eddy simulation based on theυ2-fmodel[J]. International Journal of Heat and Fluid Flow, 2014, 46(2): 84-101.

[17] 徐晶磊, 高歌, 杨焱. 基于当地流动结构的RANS/LES混合模型[J]. 航空学报, 2014, 35(11): 2992-2999. XU J L, GAO G, YANG Y. A RANS/LES hybrid model based on local flow structure[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(11): 2992-2999 (in Chinese).

[18] 王翔宇, 李栋. SST-DES在小分离流动数值模拟中的改进[J]. 北京航空航天大学学报, 2014, 40(9): 1245-1249. WANG X Y, LI D. Improved SST-DES in numerical simulation of mild separation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(9): 1245-1249 (in Chinese).

[19] 李斌, 吴颂平. 基于湍流尺度的混合RANS/LES模型[J]. 北京航空航天大学学报, 2008, 34(7): 755-758. LI B, WU S P. Hybrid RANS/LES model based on turbulent scale[J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(7): 755-758 (in Chinese).

[20] 李栋, 焦予秦, SHOV I M, 等. Detached Eddy Simulation方法模拟不同类型翼型的失速特性[J]. 航空学报, 2005, 26(4): 406-410. LI D, JIAO Y Q, SHOV I M, et al. Detached eddy simulation for airfoil stall[J]. Acta Aeronautica et Astronautica Sinica, 2005, 26(4): 406-410 (in Chinese).

[21] 白俊强, 张扬, 华俊. 一种滤波SST方法在翼型深失速模拟中的应用[J]. 航空学报, 2013, 34(5): 979-987. BAI J Q, ZHANG Y, HUA J. Application of filter-SST method in airfoil deep stall simulation[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(5): 979-987 (in Chinese).

[22] 刘周, 杨云军, 周伟江, 等． 基于RANS-LES混合方法的翼型大迎角非定常分离流动研究[J]. 航空学报, 2014, 35(2): 372-380. LIU Z, YANG Y J, ZHOU W J, et al. Study of unsteady separation flow around airfoil at high angle of attack using hybrid RANS -LES method [J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(2): 372-380 (in Chinese).

[23] DECK S. Zonal-detached-eddy simulation of the flow around a high-lift configuration[J]. AIAA Journal, 2005, 43(11): 2372-2384.

[24] FORSYTHE J R, SQUIRES K D, WURTZLER E, et al. Detached-eddy simulation of the F-15E at high alpha[J]. Journal of Aircraft, 2004, 41(2): 193-200.

[25] BROCK J M, SUBBAREDDY P K, CANDLER G V. Detached-eddy simulation of hypersonic capsule wake flow[J]. AIAA Journal, 2015, 53(1): 70-80.

[26] 杨小龙, 林铁平. 汽车外流场DES/RANS模拟研究[J]. 湖南大学学报(自然科学版), 2011, 38(1): 29-34. YANG X L, LIN T P. DES and RANS of vehicle external flow field[J]. Journal of Hunan University (Natural Science), 2011, 38(1): 29-34 (in Chinese).

[27] 谢超, 谷正气, 杨振东, 等. 不同RANS/LES混合模型的汽车气动噪声分析[J]. 汽车工程, 2015, 37(4): 440-445. XIE C, GU Z Q, YANG Z D, et al. Analysis on vehicle aerodynamic noise with different hybrid RANS/LES models[J]. Automotive Engineering, 2015, 37(4): 440-445 (in Chinese).

[28] 刘学强, 伍贻兆. 用DES数值模拟具有横向喷流的紊流流场[J]. 航空学报, 2004, 25(3): 209-213. LIU X Q, WU Y Z. The computation of the lateral jet turbulence flow using DES method[J]. Acta Aeronautica et Astronautica Sinica, 2004, 25(3): 209-213 (in Chinese).

[29] 周昊, 岑可法, 樊建人. 分离涡方法模拟浓氮气固射流两相非稳态流动特性研究[J]. 中国电机工程学报, 2005, 25(7): 1-6. ZHOU H, CEN K F, FAN J R. The numerical investigation on the transient characteristics of the gas-solid two-phase fuel rich-lean burn flow[J]. Proceedings of the CSEE, 2005, 25(7): 1-6 (in Chinese).

[30] 孙明波, 梁剑寒, 王振国. 二维凹腔超声速流动的混合RANS/LES模拟[J]. 推进技术, 2006, 27(2): 119-123. SUN M B, LIANG J H, WANG Z G. Hybrid RANS/LES simulation of the supersonic flow over two-dimentional cavities[J]. Journal of Propulsion Technology, 2006, 27(2): 119-123 (in Chinese).

[31] 汪洪波, 孙明波, 吴海燕, 等. 超声速燃烧凹腔质量交换特性的混合RANS/LES模拟[J]. 航空动力学报, 2010, 25(1): 41-46. WANG H B, SUN M B, WU H Y, et al. Hybrid RANS/LES simulation of mass exchange characteristics of cavity for supersonic combustion[J]. Journal of Aerospace Power, 2010, 25(1): 41-46 (in Chinese).

[32] 薛帮猛, 杨永. 基于两方程湍流模型的DES方法在超声速圆柱底部流动计算中的应用[J]. 西北工业大学学报, 2006, 24(5): 544-547. XUE B M, YANG Y. Technical details in applying DES method to computing supersonic cylinder-base flow[J]. Journal of Northwestern Polytechnical University, 2006, 24(5): 544-547 (in Chinese).

[33] SHUR M, SPALART P R, STRELETS M, et al. Detached-eddy simulation of an airfoil at high angle of attack[C]//4th International Symposium on Engineering Turbulence Modeling and Experiments. Amsterdam: Elsevier Science Ltd., 1999: 669-678.

[34] SHIH T H, LIOU W W, SHABBIR A, et al. A newk-εeddy-viscosity model for high Reynolds number turbulent flow[J]. Computers & Fluids, 1995, 24(3): 227-238.

[35] MENTER F R, KUNTZ M, LANGTRY R. Ten years of industrial experience with the SST turbulence model[J]. Turbulence, Heat and Mass Transfer, 2003, 4(1): 625-632.

[36] NICHOLS R H. Comparison of hybrid RANS/LES turbulence models on a circular cylinder at high Reynolds number: AIAA-2005-0498[R]. Reston: AIAA, 2005.

[37] KRAVCHENKO A G, MOIN P. Numerical studies of flow over a circular cylinder atReD=3 900[J]. Physics of Fluids, 2000, 12(2): 403-417.

[38] ONG L, WALLACE J. The velocity field of the turbulent very near wake of a circular cylinder[J]. Experiments in Fluids, 1996, 20(6): 441-453.

[39] PARNAUDEAU P, CARLIER J, HEITZ D, et al. Experimental and numerical studies of the flow over a circular cylinder at Reynolds number 3900[J]. Physics of Fluids, 2008, 20(8): 1-14.

[40] SPALART P R. Yong-person’s guide to detached-eddy simulation grids: NASA/CR-2001-211032[R]. Washington, D.C.: NASA, 2001.

[41] BUNGE U, MOCKETT C, THIELE F. Guidelines for implementing detached-eddy simulation using different models[J]. Aerospace Science and Technology, 2007, 11(5): 376-385.

[42] TRAVIN A, SHUR M, STRELETS M, et al. Detached-eddy simulations past a circular cylinder[J]. Flow, Turbulence and Combustion, 1999, 63(1): 293-313.

[43] MANSY H, YANG P M, WILLIAMS D R. Quantitative measurements of three-dimensional structures in the wake of a circular cylinder[J]. Journal of Fluid Mechanics, 1994, 270: 227-296.

[44] WILLIAMSON C H K, WU J, SHERIDAN J. Scaling of streamwise vortices in wakes[J]. Physics of Fluids, 1995, 7(10): 2307-2309.

[45] MENTER F R. Two-equation eddy-viscosity turbulence model for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605.

[46] DONG S, KARNIADAKIS G E, EKMEKCI A, et al. A combined direct numerical simulation-particle image velocimetry study of the turbulent near wake[J]. Journal of Fluid Mechanics, 2006, 569: 185-207.

[47] MA X, KARAMANOS G S, KARNIADAKIS G E. Dynamics and low-dimensionality of turbulent near wake[J]. Journal of Fluid Mechanics, 2000, 410: 29-65.

[48] FRANKE J, FRANK W. Large eddy simulation of the flow past a circular cylinder atRe=3 900[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(10): 1191-1206.

(责任编辑：鲍亚平)

＊Corresponding author. E-mail: sn_chang@buaa.edu.cn

Comparison of detached eddy simulation schemes on a subcritical flow around circular cylinder

TANG Hu1, CHANG Shinan1,*, CHENG Zhu2, MA Lan2

1.SchoolofAeronauticScienceandEngineering,BeihangUniversity,Beijing100083,China2.AircraftStrengthResearchInstituteofChina,Xi’an710065,China

Considering the requirements of simulating the flow around spray system in ground based icing test facilities, the accuracy of three detached eddy simulation (DES) schemes applied to three-dimensional subcritical flow around circular cylinder was examined through the comparison and analysis of instantaneous flow characteristics and flow statistic parameters. It is found that, from the point of instantaneous flow characterization, thek-ωReynolds averaged Navier-Stokes (RANS) branch has remarkable influence on the accuracy of shear stress transportk-ωDES (SSTk-ωDES). From the point of error range in flow statistics, the length of recirculation region and streamwise minimum velocity are the key parameters which determine the accuracy of numerical simulation on flow around circular cylinder. Compared comprehensively, the instantaneous flow characteristics and flow statistics obtained from SSTk-ωDES have well agreements with the data of experiments and large eddy simulation (LES), which thus has the potential of being applied to computing the wake turbulence of spray system in ground based icing test facilities.

turbulent dispersion; wake flow; DES; vortex structure; statistics

2016-04-07； Revised：2016-05-07； Accepted：2016-05-27； Published online：2016-06-07 08:40

URL：www.cnki.net/kcms/detail/11.1929.V.20160607.0840.004.html

s：National Natural Science Foundation of China (11372026)； Technique Innovation Foundation of Aviation Industry Corporation of China (2013F62302)

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0174

2016-04-07； 退修日期：2016-05-07； 录用日期：2016-05-27； 网络出版时间：2016-06-07 08:40

www.cnki.net/kcms/detail/11.1929.V.20160607.0840.004.html

国家自然科学基金 (11372026)； 中国航空工业集团公司技术创新基金 (2013F62302)

＊通讯作者.E-mail: sn_chang@buaa.edu.cn

唐虎， 常士楠， 成竹， 等． 亚临界圆柱绕流的DES方法比较[J]． 航空学报, 2017, 38(3): 120294. TANG H, CHANG S N, CHENG Z, et al. Comparison of detached eddy simulation schemes on a subcritical flow around circular cylinder[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(3): 120294.

V216.8

A

1000-6893(2017)03-120294-11