吸气式高超声速飞行器鲁棒非奇异Terminal滑模反步控制
2017-11-20王肖郭杰唐胜景徐倩马悦悦张尧
王肖, 郭杰,*, 唐胜景, 徐倩, 马悦悦,3, 张尧
1.北京理工大学 宇航学院, 北京 100081 2.北京宇航系统工程研究所, 北京 100076 3.北京机电工程总体设计部, 北京 100854
吸气式高超声速飞行器鲁棒非奇异Terminal滑模反步控制
王肖1, 郭杰1,*, 唐胜景1, 徐倩2, 马悦悦1,3, 张尧1
1.北京理工大学 宇航学院, 北京 100081 2.北京宇航系统工程研究所, 北京 100076 3.北京机电工程总体设计部, 北京 100854
针对含有参数摄动、外界干扰的吸气式高超声速飞行器弹性模型,设计了一种基于新型非线性干扰观测器的Terminal滑模反步控制器。将考虑弹性模态的飞行器纵向模型表示为严格反馈形式,在传统反步法的基础上采用非奇异快速Terminal滑模控制俯仰角与俯仰角速率,优化了反步法的控制结构,并实现了系统的有限时间收敛。基于跟踪微分器设计了一种新型非线性干扰观测器,并与本文所提滑模反步方法相结合,通过对包括虚拟控制量微分信号在内的不确定性进行估计与补偿,进一步提高了控制器的鲁棒性,同时解决了“微分膨胀”问题。基于Lyapunov稳定性理论证明了系统的跟踪误差于有限时间收敛至零。仿真结果表明,该控制器在存在不确定性的情况下,可以实现对参考输入的稳定跟踪。
高超声速飞行器; 滑模控制; 反步法; 非线性干扰观测器; 有限时间收敛
高超声速飞行器是指飞行速度大于5Ma的飞行器,其速度快、突防能力强,有着巨大的军事价值和经济价值。近期,装配有超燃冲压发动机的吸气式高超声速飞行器(Air-breathing Hypersonic Vehicle,AHV)成为研究发展的热点[1]。然而,此类飞行器采用的机体/发动机一体化技术以及乘波体构形使得弹性机体、推进系统以及气动特性之间的耦合更加严重,模型的非线性度更高。同时,AHV飞行包线大,飞行环境复杂,气动特性变化剧烈,模型不确定性强。因此,AHV控制器的设计面临着巨大的挑战[2-3]。
近年来,各类非线性控制算法日渐成熟,逐渐应用于AHV的控制器设计中[4-7]。其中,反步法(Backstepping)因其适用于多个积分环节串联形成的非线性系统,已广泛应用于AHV的控制系统设计。然而,传统反步法鲁棒性不强,研究者们致力于将其与其他控制方法相结合以提高其鲁棒性。文献[8]采用动态逆反步控制器,利用自适应模糊系统在线辨识系统中的不确定项,保证了控制系统的鲁棒性。文献[9]设计了一种基于RBF神经网络的反步控制器,在飞行器存在强干扰的情况下获得了理想的控制效果。文献[10]针对飞行器存在未知参数和执行器故障的问题,采用自适应反步控制方法,实现了对参考输入的鲁棒跟踪。
传统反步法所面临的另一问题是:随着系统阶数的增加,需要求取虚拟控制量的高阶微分信号,这会导致“微分膨胀”问题。针对该问题,通过采用动态面技术[11-12]或指令滤波器[13-14]来间接求取虚拟控制量及其微分信号,从而代替了对虚拟控制量的直接微分。然而,这些方法求得的虚拟控制量与理想值之间仍有误差。当系统参考指令变化较快时,跟踪误差可能很大;同时,这也增加了串级控制系统设计的复杂程度。
此外,传统AHV反步控制器中,状态量包含迎角,可以考虑使用俯仰角代替,将俯仰角与俯仰角速率一起控制,从而简化控制器的结构。针对这种结构的控制,一种有效的方法是使用Terminal滑模,但传统的Terminal滑模存在控制奇异和远离平衡点时收敛缓慢的问题[15]。鉴于此,文献[15-17]对滑模面进行了改进,但在强不确定性的情况下,系统难以稳定,且控制输入存在抖振问题。
近年来,非线性干扰观测器(Nonlinear Disturbance Observer,NDO)因其能在线实时估计系统不确定量的大小而备受关注[18-22]。其中,自抗扰控制[20-22]的核心扩张状态观测器本质就是一种非线性干扰观测器。而利用自抗扰控制中的另一理论跟踪微分器(tracking differentiator)也可设计干扰观测器。将非线性干扰观测器与滑模反步控制器相结合,能够使控制系统的鲁棒性更强。
基于以上分析,本文针对含有参数摄动、外界干扰的AHV弹性模型,设计了一种滑模反步控制器,实现了对参考输入的稳定跟踪。该控制器采用非奇异快速Terminal滑模(Nonsingular Fast Terminal Sliding Mode,NFTSM)与反步法相结合,可同时控制俯仰角与俯仰角速率,简化控制器结构的同时,实现了系统的有限时间收敛;在此基础上结合一种基于跟踪微分器的新型非线性干扰观测器,通过估计和补偿各回路中包括虚拟控制量微分在内的不确定性,提高了控制器的鲁棒性,同时避免了“微分膨胀”的问题。
1 模型描述
AHV弹性纵向运动模型如下[4-5]:
(1)

式(1)中的T、L、D、M和Ni(i=1,2,3)可表示[4]为
(2)
为了便于后续控制系统设计,将式(1)改为如下严反馈形式:
(3)
式中:θ=a+γ为飞行器俯仰角。
gV=qSCT,φ(a)cosa/m
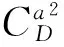



其中:dV、dγ和dQ为各回路中不确定性之和,包括参数摄动、未建模动态、外部扰动、弹性作用以及舵偏对气动力的耦合等。
由式(2)可知,飞行器所受气动力和力矩与弹性模态存在严重的耦合,设计控制系统时必须考虑到弹性模态的影响。工程中,弹性模态很难测量,本文将由弹性模态引起的气动力和力矩对各回路的影响包含在dV、dγ和dQ内,视为未知不确定性的一部分。通过干扰观测器对其进行估计与补偿,可解决弹性模态无法测量给控制器设计带来的困难。

注1 升降舵和鸭舵产生的阻力对速度回路的影响包含在dV内。升降舵产生的升力与鸭舵产生的升力抵消。鸭舵产生的俯仰力矩对俯仰角速率的影响包含在fQ内。
2 控制算法设计
2.1 非奇异快速Terminal滑模控制
考虑如下含有不确定性的仿射非线性系统:
(4)
式中:x1和x2为二阶系统的2个状态变量;u为控制输入;f(x1,x2)和g(x1,x2)为系统模型中的已知部分;d为系统不确定性,包括系统参数摄动、模型误差和外部扰动等,是关于时间t和状态x的未知函数,并满足条件|d|≤lg且lg>0,lg为不确定性的上界。
为了克服传统Terminal滑模存在奇异和收敛速度慢的缺点,采用如下非奇异快速Terminal滑模面:
s=x1+α|x1|msgnx1+β|x2|nsgnx2
(5)
式中:控制参数α>0,β>0,1

定理1 对于非线性不确定系统式(4),选取滑模面式(5),取如式(6)的控制量u,则系统状态x1、x2可在有限时间内收敛到平衡点。

(6)
式中:设计参数δ>0,k>0。

(7)
对V1取微分,然后将式(5)~式(7)代入,得
s(x2+α m|x1|m-1x2+β n|x2|n-1·
s β n|x2|n-1[d-ks-(lg+δ)sgns]
(8)
由|d|≤lg得
-kβn|x2|n-1s2-δβn|x2|n-1|s|=
(9)
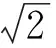

因此,相平面上任意位置的初始状态都能以有限时间收敛到滑模面。
当系统处于滑模面上时,有
x1+α|x1|msgnx1+β|x2|nsgnx2=0
(10)
变换式(10)并积分得
(11)
最终求出状态收敛时间ts为
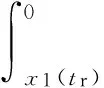
(12)
式中:x1(tr)为到达滑模面时x1的值。
由文献[24]中的定理13可得
ts (13) 于是,系统状态x1、x2可在有限时间内收敛到平衡点,总的收敛时间tend=tr+ts。定理1得证。 此外,由于1 注2 对于如下一阶系统: (14) (15) 在此条件下,按照定理1,针对二阶系统式(15),将滑模面设计为式(5)的形式: (16) 取控制律为式(6)的形式: (17) 则由定理1知,系统状态x1、x2以有限时间收敛到平衡点。 2.2 基于跟踪微分器的非线性干扰观测器 引理2[25]考虑如下系统: (18) 系统式(18)即是基于反双曲正弦函数的跟踪微分器。仿真表明,该跟踪微分器跟踪精度高、响应速度快,且能很好抑制微分信号的噪声放大现象。 引理3[26]利用跟踪微分器可设计非线性干扰观测器。考虑一阶系统式(14),相应的非线性干扰观测器可设计为 (19) (20) 由引理2和引理3,可设计一种新型非线性干扰观测器为 (21) 由文献[26]中的定理2可知,当R→∞时,该观测器可以估计几乎所有类型的扰动,并且不需要扰动的先验信息。但在实际系统中,R一般为有限值,此时R的大小决定了观测器的带宽,通过选取合适的R来选取观测器估计扰动的频谱范围。当R为有限值时,观测器收敛需要d的微分存在且有界作为前提。 注3 设计参数a1、a2、b1、b2和R对非线性干扰观测器的观测性能影响如下:①a1、b1和R越大,非线性干扰观测器的收敛速度越快,估计误差越小,但过大的a1和b1会引起不必要的超调;② 相反地,a2、b2越小,非线性干扰观测器的收敛速度越快,估计误差越小,过小的a2和b2会引起超调。 2.3 基于非线性干扰观测器的Terminal滑模控制 传统Terminal滑模的另一个缺点是由于控制律中包含符号函数,不可避免地带来输入抖振。系统式(4)中,为了消除未知不确定性d的影响,滑模控制律中引入切换增益项lgsgns,且lg越大,输入抖振幅度越大。为了减小抖振,进一步提高系统的鲁棒性,本文采用2.2节中基于跟踪微分器的非线性干扰观测器对未知不确定性进行估计和补偿。 (22) 定理2 对于非线性不确定系统式(4),选取滑模面式(5),取控制律式(22),则系统状态x1、x2可在有限时间内收敛到平衡点。 s(x2+α m|x1|m-1x2+β n|x2|n-1· (23) 与定理1中类似,利用引理1可证明系统在有限时间内收敛到滑模面s=0上。当系统处于滑模面上时,其动态特性与定理1中相同。于是,系统状态x1、x2可在有限时间内收敛到平衡点。定理2得证。 此外,控制律式(22)中不含有负指数项,控制输入不存在奇异问题。 滑模控制律式(6)中引入切换增益项(符号函数项)是为了消除未知不确定性的影响,且切换增益越大,输入抖振幅度越大。对比定理1、定理2中的控制律式(6)和式(22)可知,在通过非线性干扰观测器对不确定性d进行估计与补偿后,控制律中的切换增益项仅需补偿非线性干扰观测器对不确定性估计的误差;并且由2.2节可知,通过合理地设计非线性干扰观测器能够使其估计误差足够小,因此切换增益项也可以足够小,于是系统输入抖振也将大幅减小。当非线性干扰观测器估计效果足够理想时,取δNDO=0,可完全消除抖振。 (24) 则由定理2可知,系统状态x1、x2以有限时间收敛到平衡点。 3.1 速度控制器设计 定义速度跟踪误差eV=V-Vref,Vref表示速度参考指令。则由式(3)可得 (25) 将滑模面选取为式(16)的形式: βV|eV|nVsgneV (26) 将控制量φ设计为式(24)的形式: (27) (28) 由定理2可知,速度子系统在有限时间内收敛到eV=0。 3.2 高度控制器设计 定义高度跟踪误差eh=h-href,href表示高度参考指令。则由式(3)可得 (29) 选用式(16)形式的滑模面: βh|eh|nhsgneh (30) 取γd为虚拟控制量,将其设计为式(24)的形式: (31) 式中:αh、βh、mh、nh、kh和δh为待设计正数。 由反步法的设计思想,在航迹角回路中,以γd为参考指令,以俯仰角θ为虚拟控制量,取航迹角跟踪误差eγ=γ-γd。同时为了避免传统反步法求取虚拟控制量微分时的“微分膨胀”问题,将虚拟控制量的微分作为不确定性的一部分,则 (32) 选取滑模面: βγ|eγ|nγsgneγ (33) 将虚拟控制量θd设计为 (34) (35) 对于俯仰角和俯仰角速率系统: (36) (37) (38) 选取式(5)中的滑模面: SQ=eθ+αQ|eQ|mQsgneθ+βQ|eQ|nQsgneQ (39) 取控制量为式(22)的形式: (40) (41) 从式(40)中的实际控制量δe的形式可以看出,δe是由俯仰角指令θd解算求出的,与俯仰角速率指令Qd无关。而传统反步法一般先在航迹角回路中求出迎角指令αd,然后在迎角回路求出俯仰角速率指令Qd,最后在俯仰角速率回路中由Qd求出δe[14]。本文设计的控制方案跳过了Qd环节,从而简化了反步法的控制结构。 注5 在控制律式(27)、式(31)、式(34)和式(40)中,将参数设计为1 3.3 稳定性证明 通过合理地选取观测器和控制器参数,使得观测器收敛速度大于控制器收敛速度,从而保证观测器与控制器满足分离定理。取系统的Lyapunov函数: (42) 对式(42)微分得 (43) 将式(26)、式(27)、式(30)、式(31)、式(33)、式(34)、式(39)和式(40)代入式(43)得 (44) 将式(44)进一步展开得 SQ(eQ+αQmQ|eθ|mQ-1eQ+βQnQ|eQ|nQ-1· Shβhnh|eh|nh-1(-khSh-δhsgnSh)+ (45) βVnV|eV|nV-1|SV|- μ2|SV|-μ2|Sh|-μ2|Sγ|-μ2|SQ|≤ (46) 讨论eV、eh、eγ和eQ至少一个为零的情况。不妨设eV=0,此时μ1=μ2=0,由式(25)~式(27)可得 (47) 到达滑模面后,由于所选用的非奇异快速Terminal滑模的有限时间收敛特性,系统状态最终收敛到零,飞行速度和高度将在有限时间内跟踪上参考指令Vref和href。 3.4 控制参数设计 本文设计的控制参数主要分为两大类:一类是非线性干扰观测器设计参数,包括aj,1、aj,2、bj,1、bj,2和R(j=V,γ,θ,Q);另一类是滑模控制器参数,包括αi、βi、mi、ni、ki和δi(i=V,h,γ,Q)。 非线性干扰观测器的参数设计原则为:① 保证非线性干扰观测器的收敛速度大于控制器收敛速度,从而使观测器与控制器满足分离定理;② 保证非线性干扰观测器的估计误差足够小,以减小控制量的抖振。非线性干扰观测器具体参数对观测器性能的影响见注3。 下面讨论滑模控制器参数设计原则。参数ki和δi的大小决定了系统趋近滑模面的速度,而αi、βi、mi和ni的大小决定了滑模面上状态收敛速度。两者综合决定了系统状态的收敛速度,收敛时间具体表达形式可见定理1。但收敛速度也不是越快越好,过快的收敛速度会导致控制量的高频变化,可能引起弹性模态的高频振动,也可能超过飞行器实际物理条件的约束。δi是非线性干扰观测器对不确定性估计误差的上界,其取值应充分考虑非线性干扰观测器估计误差的大致水平,另一方面又不能太大,以避免控制输入的剧烈抖振。此外,对于高度控制器,考虑到级联系统的特性,务必使内回路控制器收敛速度大于外回路控制器收敛速度。 因此,在设计观测器与控制器参数时,要综合考虑以上各因素的影响,适当选取控制参数以满足实际系统要求。 为了验证所设计控制律的有效性与优越性,针对AHV模型式(1),将本文所设计的基于跟踪微分器、非奇异快速Terminal滑模和反步法的控制律(TD-NFTSM-BS)与使用非线性干扰观测器改进的反步法(NDO-BS)[11]作对比。飞行器具体气动数据与几何参数见文献[4]。仿真初始状态设置为:V0=2 331.7 m/s,h0=26 213 m,γ0=0°,θ0=1.55°,Q0=0 (°)/s。 速度指令Vd=2 636.5 m/s,高度指令hd=28 042 m,为避免初始控制量过大,将指令通过阻尼0.95、固有频率0.03 rad/s的二阶滤波器得到参考轨迹Vref和href。控制器参数取为:αi=1,βi=1,mi=5,ni=5/3(i=V,γ,Q);αh=1,βh=10,mh=2,nh=5/3;kV=0.1,kh=0.05,kγ=0.1,kQ=0.2;aj,1=1,aj,2=1,bj,1=0.6,bj,2=0.6(j=V,γ,θ,Q);R=10;δV=0.1,δh=0.01,δγ=0.05,δQ=0.1。 仿真中考虑气动参数、质量、转动惯量摄动增大40%,同时分别在速度、航迹角、俯仰角速率回路加入外界扰动sin(0.01πt) m/s2、0.000 2·sin(0.01πt) (°)/s和0.1 sin(0.01πt) (°)/s2。控制量限幅为 (48) 仿真结果如图1~图9所示。 图1~图4分别为速度跟踪曲线、速度跟踪误差曲线以及高度跟踪曲线、高度跟踪误差曲线。可知,所设计的TD-NFTSM-BS方法跟踪速度很快,跟踪误差在5 s内迅速收敛到零。相比之下,NDO-BS方法在前半段跟踪误差较大,收敛速度缓慢,从而验证了本文所采用非奇异快速Terminal滑模的优越性。此外,在参数摄动并存在外部干扰的情况下,两种方法都能保证最终对参考指令的跟踪,体现了方法的鲁棒性。 图5为采用TD-NFTSM-BS方法时控制量φ、δe和δc的变化曲线。可知,控制量变化连续无抖振并在合理的范围内,这样可以避免弹性模态的高频振动。初始段控制量稍大,这是系统有限时间收敛的必然结果。末段控制量呈小幅正弦波动,这与外界扰动的形式有关。 图6~图8分别为采用TD-NFTSM-BS方法时航迹角、迎角、俯仰角、俯仰角速率和弹性模态的变化曲线。可知,这些变量变化连续并保持在合理的范围内。 图9为所设计的非线性干扰观测器对系统各回路不确定性的估计曲线。可知,非线性干扰观测器对未知不确定性可以实现准确估计,这是保证控制律鲁棒性以及削弱滑模控制输入抖振的关键。 1) 基于非奇异快速Terminal滑模的反步控制器,简化了传统反步控制的结构,并能实现系统的有限时间收敛。 2) 基于跟踪微分器的新型非线性干扰观测器,可以准确估计各回路中包括虚拟控制量微分在内的不确定性,与滑模反步控制器相结合,提高了系统的鲁棒性,并避免了“微分膨胀”问题。 3) 仿真结果表明,该控制器对飞行器参数摄动和外部干扰具有较强的鲁棒性,并能实现速度和高度跟踪误差于有限时间收敛至零。 [1] HANK J M, MURPHY J S, MUTZMAN R C. The X-51A scramjet engine flight demonstration program: AIAA-2008-2540[R]. Reston: AIAA, 2008. [2] 孙长银, 穆朝絮, 余瑶. 近空间高超声速飞行器控制的几个科学问题研究[J]. 自动化学报, 2013, 39(11): 1901-1913. SUN C Y, MU C X, YU Y. Some control problems for near space hypersonic vehicles[J]. Acta Automatica Sinica, 2013, 39(11): 1901-1913 (in Chinese). [3] 方洋旺, 柴栋, 毛东辉, 等. 吸气式高超声速飞行器制导与控制研究现状及发展趋势[J]. 航空学报, 2014, 35(7): 1776-1786. FANG Y W, CHAI D, MAO D H, et al. Status and development trend of the guidance and control for air-breathing hypersonic vehicles[J]. Acta Aeronautica et Astronautica Sinca, 2014, 35(7): 1776-1786 (in Chinese). [4] FIORENTINI L. Nonlinear adaptive controller design for air-breathing hypersonic vehicles[D]. Columbus: The Ohio State University, 2010: 79-81. [5] FIORENTINI L, SERRANI A,BOLENDER M A, et al. Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(2): 402-417. [6] SUN C, HUANG Y, QIAN C, et al. On modeling and control of a flexible air-breathing hypersonic vehicle based on LPV method[J]. Frontiers of Electrical and Electronic Engineering, 2012, 7(1): 56-68. [7] ZONG Q, WANG J, TIAN B, et al. Quasi-continuous high-order sliding mode controller and observer design for flexible hypersonic vehicle[J]. Aerospace Science and Technology, 2013, 27(1): 127-137. [8] 高道祥, 孙增圻, 罗熊, 等. 基于Backstepping的高超声速飞行器模糊自适应控制[J]. 控制理论与应用, 2008, 25(5): 805-810. GAO D X, SUN Z Q, LUO X, et al. Fuzzy adaptive control for hypersonic vehicle via Backstepping method[J]. Control Theory & Applications, 2008, 25(5): 805-810 (in Chinese). [9] BU X W, WU X Y, MA Z, et al. Nonsingular direct neural control of air-breathing hypersonic vehicle via backstepping[J]. Neurocomputing, 2015, 153(1): 164-173. [10] QI R Y, HUANG Y, JIANG B, et al. Adaptive backstepping control for hypersonic vehicle with uncertain parameters and actuator faults[J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2012, 227(1): 51-61. [11] SWAROOP D, HEDRICK J K, YIP P P, et al. Dynamic surface control for a class of nonlinear systems[J]. IEEE Transactions on Automatic Control, 2000, 45(10): 1893-1899. [12] ZONG Q, WANG F, TIAN B, et al. Robust adaptive dynamic surface control design for a flexible air-breathing hypersonic vehicle with input constraints and uncertainty[J]. Nonlinear Dynamics, 2014, 78(1): 289-315. [13] FARRELL J A, POLYCARPOU M, SHARMA M, et al. Command filtered backstepping [J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1391-1395. [14] 路遥, 董朝阳, 王青. 高超声速飞行器自适应反步控制器设计[J]. 航空学报, 2015, 36(3): 970-978. LU Y, DONG C Y, WANG Q. Adaptive backstepping controller design for hypersonic vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(3): 970-978 (in Chinese). [15] 马悦悦, 唐胜景, 郭杰. 基于ESO的复合滑模面非奇异Terminal滑模控制[J]. 控制与决策, 2015, 30(1): 76-80. MA Y Y, TANG S J, GUO J. Nonsingular terminal sliding mode control with compound sliding surface based on ESO[J]. Control and Decision, 2015, 30(1): 76-80 (in Chinese). [16] YANG L, YANG J Y. Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems[J]. International Journal of Robust and Nonlinear Control, 2011, 21(16): 1865-1879. [17] 熊少锋, 王卫红, 王森. 带攻击角度约束的非奇异快速终端滑模制导律[J]. 控制理论与应用, 2014, 31(3): 269-279. XIONG S F, WANG W H, WANG S. Nonsingular fast terminal sliding-mode guidance with intercept angle constraint[J]. Control Theory & Applications, 2014, 31(3): 269-279 (in Chinese). [18] CHEN W H. Nonlinear disturbance observer enhanced dynamic inversion control of missiles[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(1): 161-166. [19] SUN H B, LI S H, YANG J, et al. Nonlinear disturbance observer-based backstepping control for airbreathing hypersonic vehicles with mismatched disturbances[J]. IET Control Theory and Applications, 2014, 8(17): 1852-1865. [20] 韩京清. 自抗扰控制器及其应用[J]. 控制与决策, 1998, 13(1): 19-23. HAN J Q. Auto-disturbances-rejection controller and it’s applications[J]. Control and Decision, 1998, 13(1): 19-23 (in Chinese). [21] GUO B Z, ZHAO Z L. On the convergence of an extended state observer for nonlinear systems with uncertainty[J]. Systems & Control Letters, 2011, 60(6): 420-430. [22] RAN M P, WANG Q, DONG C Y. Stabilization of a class of nonlinear systems with actuator saturation via active disturbance rejection control[J]. Automatica, 2016, 63: 302-310. [23] YU S, YU X, SHIRINZADEH B, et al. Continuous finite time control for robotic manipulators with terminal sliding mode[J]. Automatica, 2005, 41(11): 1957-1964. [24] POLYAKOV A, FRIDMAN L. Stability notions and Lyapunov functions for sliding mode control systems[J]. Journal of the Franklin Institute, 2014, 351(4): 1831-1865. [25] 周涛. 基于反双曲正弦函数的跟踪微分器[J]. 控制与决策, 2014, 29(6): 1239-1242. ZHOU T. Tracking differentiator based on inverse hyperbolic sine function[J]. Control and Decision, 2014, 29(6): 1239-1242 (in Chinese). [26] BU X Y, WU X Y, CHEN Y, et al. Design of a class of new nonlinear disturbance observers based on tracking differentiators for uncertain dynamic systems[J]. International Journal of Control, Automation and Systems, 2015, 13(3): 595-602. (责任编辑:张玉) *Corresponding author. E-mail: guojie1981@bit.edu.cn Robust nonsingular Terminal sliding mode backstepping control for air-breathing hypersonic vehicles WANG Xiao1, GUO Jie1,*, TANG Shengjing1, XU Qian2, MA Yueyue1,3, ZHANG Yao1 1.SchoolofAerospaceEngineering,BeijingInstituteofTechnology,Beijing100081,China2.BeijingInstituteofAstronauticalSystemsEngineering,Beijing100076,China3.BeijingSystemDesignInstituteofElectro-MechanicEngineering,Beijing100854,China A new nonlinear disturbance observer based Terminal sliding mode backstepping controller is proposed for flexible air-breathing hypersonic vehicles with parameter perturbations and external disturbances. The longitudinal vehicle model considering the elastic mode is expressed as strict feedback form. On the basis of traditional backstepping method, the nonsingular fast Terminal sliding mode is introduced to control the pitch angle and pitch rate, thus optimizing the control structure and enabling the system with finite time convergence property. A new nonlinear disturbance observer developed from tracking differentiator is then introduced to estimate and compensate the uncertainties including the derivatives of virtual control laws to improve the robustness of the controller, which avoids the explosion of differentiation terms. The system tracking error is proven to converge to zero in finite time with Lyapunov stability theory. Simulations demonstrate the effectiveness of tracking input commands with the designed controller in the presence of uncertainties. hypersonic vehicles; sliding mode control; backstepping method; nonlinear disturbance observer; finite time convergence 2016-04-05; Revised:2016-04-26; Accepted:2016-06-06; Published online:2016-06-12 14:16 URL:www.cnki.net/kcms/detail/11.1929.V.20160612.1416.012.html s:National Natural Science Foundation of China (11202024); Aeronautical Science Foundation of China (2012ZA720002) http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn 10.7527/S1000-6893.2016.0182 2016-04-05; 退修日期:2016-04-26; 录用日期:2016-06-06; 网络出版时间:2016-06-12 14:16 www.cnki.net/kcms/detail/11.1929.V.20160612.1416.012.html 国家自然科学基金 (11202024); 航空科学基金 (2012ZA720002) *通讯作者.E-mail: guojie1981@bit.edu.cn 王肖, 郭杰, 唐胜景, 等. 吸气式高超声速飞行器鲁棒非奇异Terminal滑模反步控制[J]. 航空学报, 2017, 38(3): 320287. WANG X, GUO J, TANG S J, et al. Robust nonsingular Terminal sliding mode backstepping control for air-breathing hypersonic vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(3): 320287. V448.2 A 1000-6893(2017)03-320287-13





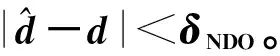



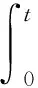
3 AHV控制器设计
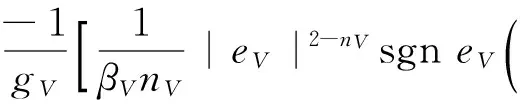




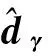










4 仿真分析
5 结 论
