低速流场中柔性悬臂板的后颤振响应

陈涛， 徐敏， 谢丹， 安效民

西北工业大学 航天学院， 西安 710072

低速流场中柔性悬臂板的后颤振响应

陈涛， 徐敏*， 谢丹， 安效民

西北工业大学 航天学院， 西安 710072

建立了一个新的非线性气动弹性模型,对低速流场中柔性悬臂板的后颤振响应特性进行了分析。建模中考虑了结构几何非线性、气动力非线性以及两者之间的强耦合效应。通过实验数据对所建立的气动弹性模型进行了验证。发现在低速流场中柔性悬臂板可能会以周期加倍的方式进入混沌运动。结构几何非线性效应和翼尖涡引起的非定常气动力效应对柔性悬臂板的结构响应有显著影响，而尾涡变形引起的非定常气动力对结构运动的影响较小。还研究了不同耦合算法的差异，给出了小展弦比大柔性结构非线性气动弹性数值仿真时耦合策略的选择依据。

低速流场； 柔性悬臂板； 后颤振； 混沌运动； 强耦合

低速流场中悬臂板的气动弹性行为可以用来解释现实中的许多现象，如机翼颤振、旗帜飘动和打鼾等。最近， Dunnmon[1]和Doaré[2]等甚至开始研究利用柔性悬壁板的颤振来收集能量用于发电。因此，低速流场中悬臂板的非线性气动弹性特性研究是一项很有意义的工作。

关于低速流场中的非线性气动弹性问题，早期的研究可以追溯到二维情形，Lee等[3]对此做过详细的综述，二维问题中极限环振荡(LCO)、混沌运动等现象都已通过数值计算或实验等手段发现。对于三维问题，非线性效应比二维情况要复杂的多。Tang[4]和Attar[5]等通过耦合非定常涡格法和计算结构动力学的方法建立了一个非线性气动弹性模型，并研究了切尖三角翼和小展弦比长方形机翼在低速流场中的极限环振荡特性。研究发现这些非线性气动弹性现象主要受结构几何非线性效应的主导。Cavallaro等[6]采用有限元和势流理论方法研究了柔性连接翼的非线性气动弹性特性。Arena等[7]采用势流理论方法研究了大柔性机翼的后颤振响应特性，他们发现流场的非定常效应会对机翼运动产生重要影响。此外，Relvas和Suleman[8]基于结构有限元方法和非定常涡格法也建立了一个非线性气动弹性模型并研究了柔性悬臂板的极限环振荡现象。国内尹维龙和田东奎[9]基于势流理论方法研究了二维柔性翼型的气动弹性特性。谢长川等[10]基于势流理论和结构有限元方法研究了柔性机翼的低速颤振特性，结果发现结构几何非线性效应对柔性翼的颤振边界有重要影响。张健和向锦武[11]基于ONERA失速气动力模型和非线性梁模型研究了柔性飞机的非线性气动弹性特性。

以上研究表明，低速流场中三维柔性结构的气动弹性建模需要考虑3种非线性效应：① 由于结构大变形引起的结构几何非线性效应；② 由于流场涡等引起的非定常气动力效应；③ 这两者的耦合效应。首先，对于结构几何非线性问题，Gordnier和Visbal[12]研究表明，气动弹性建模中遇到的主要问题是像von Karmann板理论等方法在求解几何大变形问题时会产生“锁住”效应。其次，对于低速气动弹性问题，目前国际上广泛采用势流理论方法进行非定常气动力建模。虽然有更精确的方法如CFD等，但在低速问题中柔性结构响应周期往往较长，采用CFD方法会消耗大量计算时间。Murua等[13]的研究表明非定常涡格法在计算准确性和计算效率2个方面都能达到较满意的效果，国内许多学者也采用非定常涡格法研究低速飞行器的非定常气动力建模问题[14-15]，该方法还常用于气动力非定常效应很强的扑翼气动弹性现象研究[16-17]。最后，关于结构几何非线性与非定常气动力的耦合效应，Piperno和Farhat[18]的研究表明，气动弹性建模中采用松耦合策略会产生一定的数值误差。对于柔性翼这样非线性特性很强的气动弹性问题，松耦合策略可能会引起较大的误差。

如前所述，Attar和Relvas等只研究了柔性壁板的周期性极限环振荡现象，虽然他们都考虑了结构和气动力的非线性效应，但对于耦合策略的影响仍然有待研究。本文的工作是对Attar[5]和Relvas[8]等研究工作的进一步扩展。在本文的气动弹性建模中不仅详细考虑了结构几何非线性效应带来的“锁住”问题和非定常气动力问题，还考虑了结构与气动力之间的强耦合问题。其中，结构建模采用一种多变量有限元方法，非定常气动力建模采用非定常涡格法，采用强耦合策略实现结构和气动力求解器的耦合。本文的结构安排如下，首先给出新的非线性气动弹性建模过程，然后通过柔性三角翼极限环振荡的仿真对所提出的气动弹性模型进行验证，最后对柔性悬臂板后颤振响应以及相关的非线性影响因素给出分析结果。

1 结构几何非线性建模

柔性悬臂板的结构建模采用多变量实体壳单元。这种单元的有限元列式过程简要介绍如下。

实体壳单元是一种多变量的有限元单元，这种单元的位移场、应变场和应力场是相互独立的，可以分别假设独立的插值模式。其有限元列式基于三场FHW变分原理[19]：

(1)

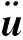
对于上述处理方法，笔者早期研究工作已经证明这是一种解决“锁住”效应的有效手段[20]。当给定了位移、应变和应力的插值形函数以后，就可以对式(1)进行离散。本文的算法中采用一种无条件稳定的能量-动量守恒算法作为时间推进算法，采用Newton-Raphson算法对式(1)进行线性化：

(2)

(3)

2 非定常气动力建模

与Attar[5]和Relvas[8]等相同，本文采用非定常涡格法进行非定常气动力建模。该方法假设结构周围的流动是无旋附着流，并且不考虑黏性效应。对于本文的悬臂板问题，非定常涡格法的非线性特性主要体现在以下3个方面：① 结构表面的涡格跟随结构变形而非线性地改变形状和位置。② 机翼尾部拖出的尾涡可以自由变形。③ 随着结构的变形，可能会有翼尖涡不断拖出并卷起。在本文的研究中，翼尖涡的拖出方式与尾涡的拖出方式相同。这种翼尖涡模型在三角翼的相关研究中已被证明是一种有效的翼尖涡模拟方法[21]。在后面的数值仿真中会发现，翼尖涡效应其实对结构的气动弹性响应有很大影响。但是在Relvas等[8]的研究中并没有考虑翼尖涡效应，因此，本文是对其研究工作的拓展。下面简要介绍非定常涡格法的求解流程。

定常涡格法的求解过程主要是为了得到结构表面的涡量强度分布，这些涡量强度用来计算结构表面的气动力载荷。首先，将结构表面用一系列涡格离散，在每一个涡格中，涡的强度为常量。每一个涡格片段的涡强度由共享该片段的相邻2个涡格所决定。通过Biot-Savart定律可以求解每一个涡格片段的诱导速度场。随着时间的推移，结构表面的涡会从结构后缘拖出形成尾涡。刚拖出的尾涡强度与相邻的结构表面涡强度相同，当结构表面的涡拖出形成尾涡后，涡的强度保持不变。非定常涡格法通过满足物面无穿透边界条件计算得到物面的涡强分布：

[V∞+Vbound(r,t)+Vwake(r,t)]·n=0

AΓbound=Rhs

(4)

式中：Vbound和Vwake分别为结构表面和尾涡中的诱导速度；r为位置向量；t为时间；n为结构表面的单位法向量；A为气动力影响系数矩阵；Γbound为待求解的未知涡量向量；Rhs为残差向量。当物面涡量求得以后，结构表面的空气压强可由Bernoulli方程求解得到：

(5)

式中：Φ为速度势函数；p为压强；V∞和p∞分别为远场处的速度和压强。

结构上下表面的压强差表达式为

Δp=pu-pl=ρ∞[Vu·Vu-Vl·Vl+

(6)

式中：Δp为压强差；pu和pl分别为结构上下表面的压强；Vu和Vl分别为结构上下表面的速度；ru和rl分别为结构上下表面的位置向量。

由压强差便可求出对应的气动力为

Fi=ΔpiAini

(7)

3 非线性气动弹性建模

基于上述非线性有限元求解方法和非定常气动力求解方法可以建立柔性壁板的气动弹性模型。下面简要介绍建模中所采用的耦合策略和结构/流场求解器之间的数据交换方法。

3.1 耦合策略

众所周知，传统的松耦合策略会产生时间滞后效应。这会导致在每一个时间步计算得到的结构/流体交界面的位置不准确。然而，在引言中所提到的所有关于柔性悬臂板的研究都是采用松耦合算法。本文的气动弹性建模采用耦合精度更高的强耦合策略(见图1)，在每一个时间步内引入预估-校正方法来提高结构/流体交界面位置的计算精度。图1中UVLM表示非定常涡格法气动力求解器，FEM表示有限元求解器。

内迭代的收敛标准给定为相邻两次求得的结构位移向量的相对误差小于1%。此外，在实际的数值算法实现中还应给定最大内迭代步数，以防止出现永远不收敛的情况，不过在本文的研究中没有出现这种不收敛的问题。关于上述的强耦合算法需要指出的是当最大内迭代步数给定为1时，强耦合算法将自动退化为松耦合算法。本文强耦合算法的最大内迭代步数给定为10，实际中发现所有内迭代计算均会在10步以内达到收敛。

3.2 数据交换方法

在非线性气动弹性建模中，结构和流体求解器之间的数据交换方法不仅影响计算速度，更影响计算精度，特别是当结构变形很大时(例如极限环振荡等)，这一问题更加突出。本文采用径向基函数方法实现气动网格的变形[20]，这一方法非常适合于大变形过程的动网格插值。气动力的插值与结构位移场插值不同，它需要保证插值前后力场的等效，即总的力和力矩需要保持守恒。本文采用有限元形状函数插值方法实现气动力的插值。

4 数值计算

本节首先对上述所建立的非线性气动弹性模型进行验证，在此基础上对柔性悬臂板的后颤振特性进行数值仿真并给出分析结果。

4.1 非线性气动弹性模型的验证

通过一个三角翼极限环振荡(LCO)的数值仿真与实验结果的对比对所提出的非线性气动弹性模型进行验证。该模型是一个45° 的直角三角形平板，厚度为1.6 mm，翼根中部60%的部位受到固支约束。弹性模量为3.3 GPa，密度为1 299 kg/m3[6]。图2为该三角翼模型的示意图，V∞为来流速度。

经过网格收敛性分析后，气动弹性仿真的结构有限元网格共有819个实体壳单元。气动网格的大小为60×20(弦向×展向)。尾涡的长度取为弦长的4倍。

图3给出了在1° 迎角时机翼翼尖面外方向极限环振荡的最大速度对比结果。计算所得该三角翼的颤振速度为23.0 m/s，实验值为24.0 m/s。

图3表明在来流速度小于26.0 m/s时，本文的计算结果比Attar等[5]的计算结果要大，两者之间的差别随着流速的增大而逐渐减小。在较高的来流速度时，计算结果与实验结果非常接近，并且与Attar等[5]采用高精度有限元方法的计算结果也非常接近。在较低的速度范围时，计算的颤振点和极限环振荡结果与Cavallaro等[6]的结果比较接近。需要指出的是在较低的来流速度范围时，本文计算结果与其他两个计算结果的差别主要是由于对结构阻尼的不同处理导致的。Attar[5]和Cavallaro[6]等分别采用了不同的结构阻尼形式，由于非线性气动弹性计算中结构阻尼的影响是一个比较复杂的问题，目前国际上仍没有定论，因此本文没有考虑结构阻尼。从计算结果的对比来看，本文所提出的非线性气动弹性模型能较好地模拟大幅值的极限环运动。

需要指出的图3中本文的计算结果采用的是强耦合策略，这主要是为了验证前文所建立的强耦合策略的正确性。强耦合策略由于带有内迭代过程而比较耗时，对于这里的三角翼模型，传统松耦合策略与强耦合策略的计算结果也比较接近，见图4。

由于本文的气动弹性建模借鉴并改进了Relvas等[8]的方法，因此有必要将本文方法与其进行对比。文献[8]中研究的方形悬臂板模型展长(弦长)为0.3 m，板厚度为1 mm，材料为铝合金，计算初始迎角为0°。图5给出了采用Nastran线性分析方法得到的颤振V-g图，图6给出了本文的计算结果。由图5可知，Nastran计算的颤振速度为53.7 m/s，由图6可知，本文的计算结果为57.5 m/s。文献[8]的计算结果为42.0 m/s，对比可知，本文结果与Nastran的相对误差为7.08%，文献[8]的结果与Nastran的相对误差为21.79%。计算结果表明，本文的方法用于方形悬臂板后颤振响应分析是可行的。

4.2 柔性悬臂板的非线性气动弹性特性

经过实验数据验证以后，将所建立的气动弹性模型用于柔性悬臂板(图7)的后颤振响应分析。板的厚度为0.5 mm，材料属性如下：弹性模量为71 GPa，密度为2 800 kg/m3，泊松比为 0.33。需要说明的是文献[8]中的方形悬臂板模型偏硬，不适合于较大幅值的极限环振荡研究，而本文第2个算例主要是为了研究较大幅度的极限环振荡，因此本文研究的悬臂板模型尺寸在文献[8]的基础上进行了调整。在数值仿真之前，通过网格收敛性分析确定采用的计算网格。最终使用的结构网格数量为30×30(弦向×展向)，对应的气动力计算网格数量为40×40。计算过程中尾涡的长度为弦长的4倍。

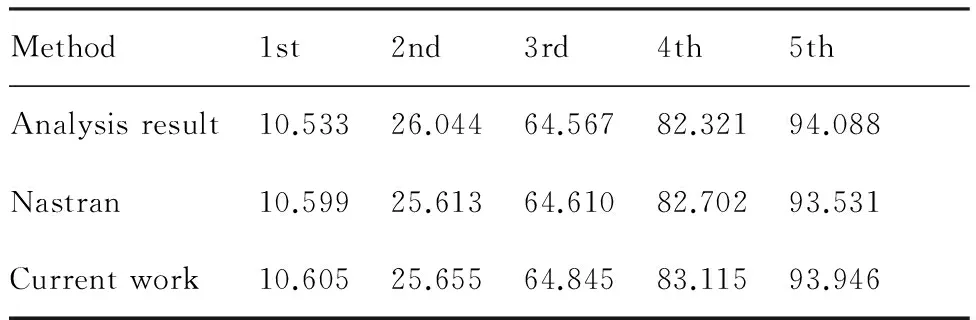
对柔性悬臂板进行气动弹性数值仿真，初始迎角为0°。表1给出了本文计算的结构固有频率和解析解[22](双向梁函数组合级数逼近法)以及Nastran计算结果的对比。图8给出了Nastran的颤振分析结果。图9给出了来流速度分别为38.3、46、54、58、62、66 m/s时前缘翼尖的结构位移响应。

由表1可知，本文采用实体壳单元计算的结构固有频率与解析解和Nastran的计算结果非常接近，与解析解的最大误差仅为1.49%(二阶)。由图8可知，Nastran分析的结构颤振边界为35.7 m/s，颤振发生的机理为二阶扭转模态发散。图9(a)表明本文基于有限元和涡格法计算的颤振边界为38.3 m/s，两者之间的相对误差为6.79%。

Method1st2nd3rd4th5thAnalysisresult10.53326.04464.56782.32194.088Nastran10.59925.61364.61082.70293.531Currentwork10.60525.65564.84583.11593.946

结构响应曲线图9表明，当来流速度高于颤振速度时，结构会发生极限环振荡。当来流速度高于54 m/s时，结构响应变得非常复杂。为了更好地分析结构响应随来流的变化趋势，图10给出了相应的相平面图。

相平面图表明，当来流速度为46 m/s时，结构响应形式为周期性的极限环振荡。当来流速度为54 m/s时，结构响应形式为准周期的极限环振荡。当来流速度为58 m/s时，结构响应出现周期加倍现象。当来流速度增大到62 m/s和66 m/s时，结构响应的规律变得非常复杂。笔者早期关于超声速流中壁板颤振的研究表明这种运动形式的变化是一种进入混沌运动的路径[23]。因此，本文首次发现了低速流场中三维柔性悬臂板很有可能也会以周期加倍的方式进入混沌运动。不过由于本文计算得到的时域响应结果步数有限，尚不能断定一定发生了混沌运动，定量的证明将在后续工作中采用降阶的方法进行研究。

从位移响应曲线(图9)还可以看出，在较大来流速度下，结构首先经历一个较大幅值的瞬态响应过程，然后收敛到稳态响应。需要指出的是，本文在气动弹性建模中没有考虑结构阻尼。另外，根据国际权威学者Hallissy和Cesnik[24]的研究，势流理论与高精度的气动力计算方法(如CFD方法等)相比气动阻尼偏小，这可能导致结构的瞬态响应幅值偏大。在Cavallaro等[6]关于柔性连接翼非线性气动弹性特性的研究中也发现了类似的瞬态响应幅值很大的情况，可见这是采用涡格法计算时的一种普遍现象。由于本文主要研究的是结构稳态响应特性，因此有必要考察结构瞬态响应对稳态响应的影响。

图11给出了分别采用结构一阶模态和二阶模态作为有限元计算的初始速度扰动时结构位移响应的对比。由图可知，结构在不同初始扰动激励下经历了不同的瞬态响应过程，但最终的稳态响应非常接近。因此说明结构瞬态响应不会对稳态响应造成很大影响。

以上研究表明低速流场中柔性悬臂板的后颤振运动存在很强的非线性特性，因此有必要对其中的非线性因素进行深入研究。下面将从结构几何非线性、气动力非线性以及耦合方式的影响3个方面进行分析。

图12给出了悬臂板在来流速度为46 m/s时考虑和不考虑结构几何非线性效应的计算结果对比，由图可知在悬臂板的后颤振响应中结构几何非线性效应的影响非常大。

为了进一步分析结构几何非线性效应对后颤振响应的影响，表2给出了在稳态响应阶段结构最大位移处计算的模态频率。可以看出，随着来流速度的增加，结构在最大位移处的一阶模态频率变化较小，二阶及高阶模态频率变化较大。在来流速度为54 m/s时，结构极限环振荡最大位移达到了板厚度的4倍左右，此时结构二阶模态频率增大了约10%。图12中采用线性结构模型的时域响应在t=0.3 s时结构最大位移已达到板厚度的5倍左右，此时结构几何非线性效应已经非常明显。

几何非线性效应主要是由结构内部应力对结构刚度的影响造成的，图13给出了表2中各来流速度对应的结构Von Mises应力分布。由图可知，当来流速度从38.3 m/s增大到46 m/s时，结构内部应力最大值由0.06 MPa增大到了2.4 MPa，此时结构刚度产生了较大变化，几何非线性效应已非常明显。

除了结构几何非线性，气动力非线性可能也会对柔性悬臂板的后颤振响应产生重要影响。下面主要考察尾涡和翼尖涡对非线性气动力的贡献。图14给出了考虑翼尖涡和不考虑翼尖涡的计算结果对比。图15给出了在来流速度为66 m/s不考虑翼尖涡时结构稳态响应的变形情况。图16 给出了分别采用自由变形尾涡模型和平面尾涡模型的计算结果。需要指出的是，此时为了单独考察尾涡变形的影响，数值计算时没有考虑翼尖涡模型。

当不考虑翼尖涡时(图14虚线)，结构的稳态响应形式为动态屈曲。虽然初始迎角为0°，但在瞬态响应过程中，结构产生了扭转变形(图15)，翼面上当地迎角不为0°，所产生的升力使得结构最终在某一平衡位置附近做幅值非常小的动态屈曲运动，这种现象在笔者早期关于超声速气流中悬臂板的混沌运动研究中发现过(见文献[23])。但考虑翼尖涡后，结构响应形式完全不同，图14表明是否考虑翼尖涡会对计算结果产生重要影响。图16表明是否考虑尾涡的变形对结构响应几乎没有影响。由以上分析可知，翼尖涡对非线性气动力的贡献较大，而尾涡的自由变形引起的气动力非线性效应较小。

表2 变形最大位移处结构模态频率

Table 2 Structural modal frequencies at position of maximum deformation Hz

Inflowvelocity/(m·s-1)1st2nd3rd4th5th010.60525.65564.84583.11593.94638.310.60625.66364.92983.19294.0564610.62626.98265.33083.54095.0025410.65428.25965.77484.80295.8795811.13441.06678.044108.315119.752

图17给出了在来流速度为54 m/s和66 m/s时分别采用松耦合、改进的松耦合以及强耦合策略的计算结果对比。这里的改进松耦合策略为Relvas和Suleman[8]在研究相似柔性悬臂板非线性气动弹性问题时所采用的耦合方式。由图可知，在较低的来流速度54 m/s时，改进的松耦合方式与强耦合方式的计算结果非常接近，而松耦合算法与强耦合算法的差异随着时间的推移会逐渐增大。在较高的来流速度66 m/s时，不管是松耦合还是改进的松耦合方式与强耦合方式的差别都是非常大的。

仔细分析还发现，在数值仿真过程中前述柔性三角翼与柔性悬臂板在最大来流速度时结构的位移响应均达到了板厚度的20倍左右(图4和图9(f))，因此，2个模型的几何非线性效应都是很强的。但在柔性三角翼的研究中，当来流速度较高时，不同的耦合策略计算得到的位移响应差别不大。而对于柔性悬臂板模型，不同的耦合策略计算得到的位移响应相差却很大。2个模型的主要区别在于气动力非线性效应的强弱，对于柔性三角翼，由于不存在翼尖涡引起的非线性气动力，因此，其气动力非线性效应要弱于柔性悬臂板。据此可知，在小展弦比大柔性结构的非线性气动弹性数值仿真时，当只有结构几何非线性效应占主导地位时，不同耦合策略的计算结果差别可能不是很大。当结构几何非线性与气动力非线性效应均较强时松耦合策略和改进的松耦合策略都会引起很大的误差。

5 结 论

建立一个新的非线性气动弹性模型对低速流场中柔性悬臂板的后颤振特性进行了数值仿真。结构几何非线性问题采用多变量有限元方法求解，非定常气动力采用非定常涡格法求解，实现了结构与气动力求解器之间的强耦合算法。采用柔性三角翼模型对所提出的气动弹性模型进行了验证，结果表明，对于大柔性结构的非线性气动弹性问题，所提出的算法可以给出较好的仿真结果。

首次发现了在低速流场中三维柔性悬臂板可能会以位移响应周期加倍的形式进入混沌运动。数值仿真结果表明，在柔性悬臂板的后颤振响应中，结构几何非线性效应和气动力非线性效应对结构运动都有很大影响。其中，气动力非线性效应主要由翼尖涡引起，而尾涡的变形对非线性气动力的贡献相对较小。在小展弦比大柔性结构的非线性气动弹性数值仿真时，当只有结构几何非线性效应占主导地位时，松耦合策略与强耦合策略的计算结果可能差别不是很大，此时可以采用松耦合策略或改进的松耦合策略。当结构几何非线性与气动力非线性效应均较强时必须采用强耦合策略。

需要说明的是本文目前只是初步研究了结构几何非线性、气动力非线性和耦合策略对柔性结构非线性气动弹性仿真的影响。下一步的工作将对其他非线性因素如结构阻尼效应等进行研究。另外，还将开展相关的风洞试验研究。

[1] DUNNMON J A, STANTON S C, MANN B P, et al. Power extraction from aeroelastic limit cycle oscillations[J]. Journal of Fluids and Structures, 2011, 27(8): 1182-1198.

[2] DOARÉ O, MICHELIN S. Piezoelectric coupling in energy-harvesting fluttering flexible plates: Linear stability analysis and conversion efficiency[J]. Journal of Fluids and Structures, 2011, 27(8): 1357-1375.

[3] LEE B H K, PRICE S J, WONG Y S. Nonlinear aeroelastic analysis of airfoils: Bifurcation and chaos[J]. Progress in Aerospace Sciences, 1999, 35(3): 205-334.

[4] TANG D, DOWELL E H, HALL K C. Limit cycle oscillations of a cantilevered wing in low subsonic flow[J]. AIAA Journal, 1999, 37(3): 364-371.

[5] ATTAR P J, DOWELL E H, WHITE J R. Modeling the LCO of a delta wing using a high fidelity structural model：AIAA-2004-1692[R]. Reston: AIAA, 2004.

[6] CAVALLARO R, IANNELLI A, DEMASI L, et al. Phenomenology of nonlinear aeroelastic responses of highly deformable joined-wings configurations: AIAA-2014-1199[R]. Reston: AIAA, 2014.

[7] ARENA A, LACARBONARA W, MARZOCCA P. Nonlinear aeroelastic formulation and postflutter analysis of flexible high aspect ratio wings[J]. Journal of Aircraft, 2013, 50(6): 1748-1764.

[8] RELVAS A, SULEMAN A. Fluid-structure interaction modelling of nonlinear aeroelastic structures using the finite element corotational theory[J]. Journal of Fluids and Structures, 2006, 22(1): 59-75.

[9] 尹维龙, 田东奎. 柔性翼型的气动弹性建模与颤振特性分析[J]. 哈尔滨工业大学学报, 2012, 44(9): 69-72. YIN W L, TIAN D K. Aeroelastic modeling and flutter characteristics of flexible aerofoil[J]. Journal of Harbin Institute of Technology, 2012, 44(9): 69-72 (in Chinese).

[10] 谢长川, 吴志刚, 杨超. 大展弦比柔性机翼的气动弹性分析[J]. 北京航空航天大学学报, 2003, 29(12): 1087-1090. XIE C C, WU Z G, YANG C. Aeroelastic analysis of flexible large aspect ratio wing[J]. Journal of Beijing University of Aeronautics and Astronautics, 2003, 29(12): 1087-1090 (in Chinese).

[11] 张健, 向锦武. 柔性飞机非线性气动弹性与飞行动力学耦合静、动态特性[J]. 航空学报, 2011, 32(9): 1569-1582. ZHANG J, XIANG J W. Static and dynamic characteristics of coupled nonlinear aeroelasticity and flight dynamics of flexible aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(9): 1569-1582 (in Chinese).

[12] GORDNIER R E, VISBAL M R. Development of a three-dimensional viscous aeroelastic solver for nonlinear panel flutter[J]. Journal of Fluids and Structures, 2002, 16(4): 497-527.

[13] MURUA J, PALACIOS R, GRAHAM J M R. Applications of the unsteady vortex-lattice method in aircraft aeroelasticity and flight dynamics[J]. Progress in Aerospace Sciences, 2012, 55(5): 46-72.

[14] 刘燚, 谢长川, 王立波, 等. 柔性飞机大变形曲面气动力计算及配平分析[J]. 工程力学, 2015, 32(10): 239-249. LIU Y, XIE C C, WANG L B, et al. Nonplanar aerodynamic computation and trim analysis under large deflection of flexible aircraft[J]. Engineering Mechanics, 2015, 32(10):239-249 (in Chinese).

[15] 宋磊, 杨华, 解静峰, 等. 基于改进涡格法的飞翼布局飞机稳定性导数计算[J]. 南京航空航天大学学报, 2014, 46(3): 457-462. SONG L, YANG H, XIE J F, et al. Predicting stability derivatives of flying wing aircraft based on improved vortex lattice method[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2014, 46(3): 457-462 (in Chinese).

[16] ROCCIA B A, PREIDIKMAN S, MASSA J C, et al. Modified unsteady vortex-lattice method to study flapping wings in hover flight[J]. AIAA Journal, 2013, 51(11): 2628-2642.

[17] 贺红林, 周翔. 柔性扑翼非定常涡格法气动力计算的改进与实现[J]. 航空学报, 2010, 31(6): 1121-1126. HE H L, ZHOU X. Implementation of an improved unsteady vortex lattice method for flexible flapping-wing aerodynamic computation[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(6): 1121-1126 (in Chinese).

[18] PIPERNO S, FARHAT C. Partitioned procedures for the transient solution of coupled aeroelastic problems-Part II: Energy transfer analysis and three-dimensional applications[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190(24-25): 3147-3170.

[19] VU-QUOC L, TAN X G. Optimal solid shells for non-linear analysis of multilayer composites. 1. Static[J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192(9-10): 975-1016.

[20] CHEN T, XU M, XIE L. Aeroelastic modeling using geometrically nonlinear solid-shell element[J]. AIAA Journal, 2014, 52(9): 1980-1993.

[21] LEVIN D, KATZ J. A vortex-lattice method for the calculation of the nonsteady separated flow over delta wings: AIAA-1980-1803[R]. Reston: AIAA, 1980.

[22] 曹志远. 板壳振动理论[M]. 北京：中国铁道出版社, 1989: 455-457. CAO Z Y. Vibration theory of plates and shells[M]. Beijing: China Railway Press, 1989: 455-457 (in Chinese).

[23] XIE D, XU M, DAI H, et al. Observation and evolution of chaos for a cantilever plate in supersonic flow[J]. Journal of Fluids and Structures, 2014, 50(6): 271-291.

[24] HALLISSY P B, CESNIK C E S. High-fidelity aeroelastic analysis of very flexible aircraft: AIAA-2011-1914[R]. Reston: AIAA, 2011.

(责任编辑：李明敏)

＊Corresponding author. E-mail: xumin@nwpu.edu.cn

Post flutter response of flexible cantilever plate inlow speed flow field

CHEN Tao, XU Min*, XIE Dan, AN Xiaomin

SchoolofAstronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China

A new nonlinear aeroelastic model is established for the analysis of post flutter behavior of the flexible cantilever plate in low speed flows. Geometric nonlinearity, aerodynamic nonlinearity as well as the strong coupling effect between geometric and aerodynamic nonlinearities are considered in the modeling. The aeroelastic model is verified with experimental data. The study shows that the flexible cantilever plate in low speed flows can enter into chaotic movement by means of periodic doubling in structural response. It is found that geometric nonlinearity and the unsteady aerodynamic effect caused by tip vortexes have significant impact on the structural response, while the unsteady aerodynamic force caused by deformation of wake vortexes has slight impact on the structural response. Different coupling strategies are also investigated to provide a reference for the selection of coupling strategy in nonlinear aeroelastic simulations of low-aspect-ratio flexible structures in low speed flows.

low speed flow field; flexible cantilever plate; post flutter; chaotic movement; strong coupling

2016-03-11； Revised：2016-10-10； Accepted：2016-11-14； Published online：2016-11-22 10:56

URL：www.cnki.net/kcms/detail/11.1929.V.20161122.1056.002.html

s：National Natural Science Foundation of China (11202165, 11402212)

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0296

2016-03-11； 退修日期：2016-10-10； 录用日期：2016-11-14； 网络出版时间：2016-11-22 10:56

www.cnki.net/kcms/detail/11.1929.V.20161122.1056.002.html

国家自然科学基金 (11202165, 11402212)

＊通讯作者.E-mail: xumin@nwpu.edu.cn

陈涛， 徐敏， 谢丹， 等． 低速流场中柔性悬臂板的后颤振响应[J]． 航空学报, 2017, 38(3): 120215. CHEN T, XU M, XIE D, et al. Post flutter response of flexible cantilever plate in low speed flow field[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(3): 120215.

V211.47

A

1000-6893(2017)03-120215-14