新型三轮大车机构轮轨动力学响应分析

张 氢,陈 淼,孙 峰,秦仙蓉,孙远韬

(同济大学 机械与能源工程学院,上海 201804)

国家科技支撑计划资助项目(2015BAF06B05)

张 氢(1967—),男,教授,博士.E-mail:zhqing_tj@126.com

新型三轮大车机构轮轨动力学响应分析

张 氢,陈 淼,孙 峰,秦仙蓉,孙远韬

(同济大学 机械与能源工程学院,上海 201804)

针对运输需求的日益提高，使得轨道式集装箱起重机大车行走机构与轨道间的动力作用进一步恶化,严重影响机构零部件及轨道的使用寿命等问题,提出一种新型轨道式三轮大车机构的设计方案.利用车架和连杆平衡机构代替原有平衡梁结构,以达到降低大车高度,得到良好的大车行走机构动力学性能的目的.为验证新型结构设计的合理性,基于拉格朗日动力学方法,建立并推导了新型大车行走机构的动力学方程,建立了轨道错牙接头、宽轨缝接头和焊缝接头的数学激励模型,研究其在3类轨道缺陷激励下的轮轨垂向作用力的响应.为验证轮轨耦合动力学模型的正确性和合理性,对其进行了虚拟样机仿真模型的建立和分析.研究表明，结构优化后的新型大车机构具有良好的轮轨动力学特性,有效降低了大车行走机构高度.

轮轨垂向力; 轮轨接触刚度; 动力学模型; 错牙接头

平衡梁均载型大车行走机构一般安装于起重机支腿位置,以实现起重机的均载运输,被广泛应用于各种港口轨道式起重机中[1].随着港口装卸运行速度的提高和运输重量的增大,大车与轨道间的动力作用也进一步恶化,承载结构也会受到动力附加载荷的作用,从而引起整机加剧振动,影响使用性能,加速结构的疲劳,这对起重机行走机构零部件及轨道的使用寿命都极为不利[2].

大车行走机构的动力学性能取决于结构参数、结构构型及轮轨接触状态等.为得到良好的轮轨动力学特性,减少因轨道冲击带来的不利影响,国内外学者以优化整机质量和高度等结构参数为目标，对大车行走机构构型进行了研究.常见三轮平衡梁式大车机构如图1所示,主要由两轮台车、单轮及平衡梁组成[3].2005年,日本德瀛号1 700 t浮吊的行走机构采用了连杆机构代替平衡梁结构以降低大车高度,如图2所示,连杆及从动轮组成的连杆均载机构能在轨道不平整时调整车轮位置,减小不利冲击.由于连杆所连接的两个车轮容易浮动,不便安装电机,只能作为从动轮,因此降低了大车的驱动能力和工作效率.2009年,上海振华重工(集团)股份有限公司应用连杆平衡装置设计了三轮大车行走机构,该机构同样是以替代平衡梁结构的方法降低了大车高度,从而减轻整机质量,减缓冲击,但偏心曲轴的存在使得各轮轮压偏差较大,部分零部件承受较大载荷从而降低寿命[4].

图1 平衡梁均载型三轮大车行走机构Fig.1A rail mounted three-wheeled gantrywith balancing linkage

图2 日本德瀛号三轮大车行走机构原理图Fig.2The structure of ‘Deying’ rail mountedthree-wheeled gantry

本文提出一种新型轨道式三轮大车行走机构构型方案,并建立了新型大车行走机构轮轨垂向耦合动力学模型,基于拉格朗日动力学方法推导了系统的动力学方程,利用Hertz非线性弹性接触理论和有限元方法计算了各部分刚度,分析其在轨道常见缺陷激励下的动力学响应，再建立动力学仿真模型对计算结果进行仿真验证.

1 机构描述

在现有设计方案上,根据运动链再生创新设计理论[5]，提出了新型三轮大车行走机构的构型方案.整机设计结构如图3所示,机构由车架、车轮架、车轮和连杆组成,利用车架代替原有机构中的两轮台车和平衡梁,降低了大车高度.同时利用连杆平衡机构连接车轮B与车轮C,根据受力分析易知三轮承受地面支持力相等,即实现了三轮轮压均载,有利于大车在运行过程中的载荷合理分配.同时,合理设置了各铰接点的位置,避免使用大直径轴承,简化构造,各车轮也可作为主动轮,增加了大车驱动力.

图3 新型三轮大车行走机构设计方案Fig.3 The new rail mounted three-wheeled gantry

2 大车行走机构动力学分析

2.1垂向动力学模型

轮轨动力学可以分为垂向、横向和纵向耦合动力学3个方面.轮轨垂向耦合动力学主要研究轮轨系统在各种垂向轮轨激扰作用下，动力响应及其轮轨动力作用的特征[6].

新型轨道式大车行走机构轮轨动力学模型主要由车体子模型和轨道子模型构成,如图4所示.车体动力学模型由钢构系、车架、轮系和元件连接处的弹簧阻尼系统构成,模型中考虑了车架的沉浮振动和点头振动,由于机构上部联接起重机钢结构(命名为钢构系)，其角位移被整机其他部分限制,故不考虑其角位移变化.此外,车轮架2与车轮架3被简化为刚性杆,3个轮系也被视为刚体质量块.至此,该动力学模型中一共有6个自由度,分别为3个轮系和钢钩系的垂向位移x1,x2,x3,x5及车架的垂向位移和角位移x4,θ.轨道模型采用了离散化的模型,轨道被简化处理成各轮对下的刚性体单元,单元之间无关联.

图4 新型轨道式三轮大车行走机构垂向力学模型Fig.4Vertical mechanical model of the new railmounted three-wheeled gantry

大车车轮与轨道之间为非线性弹性接触,但根据文献[6]在进行轮轨垂向随机振动分析时,可以将轮轨系统视为线性弹簧阻尼系统.为简化计算,这里将轮轨接触处理为弹簧阻尼系统.

力学模型中广义坐标x1,x2,x3,x4,x5及θ取各自的静平衡位置为坐标原点.三轮大车行走机构的动能和势能函数可写为

(1)

(2)

式中:m1,m2,m3,m4及m5分别为轮系1、轮系2、轮系3、车架和钢构系的质量;J2,J3和J4分别为轮系2绕铰点b、轮系3绕铰点c和车架绕质心的转动惯量;k0i,c0i(i=1,2,3)分别为轮系与轨道间接触刚度和接触阻尼;kj,cj(j=1,2,3,4,5)分别为轮系与车架、轮系之间、车架与钢构系间的支承刚度和支承阻尼;t1为车轮架2产生的角位移相对于轮系2位移的线性系数;t2为铰点g的位移相对于轮系3位移的线性系数.

根据拉格朗日动力学方程,可以得到计算系统广义质量和广义刚度的表达式:

式中:EK为系统动能函数;EP为势能函数;qi为广义坐标.因此,系统的质量矩阵及刚度矩阵可写为

将轨道对车轮的激励转化为等效力施加于3个车轮上,等效激励力分别为

广义坐标为

外部激励为

p(t)=[f1(t)f2(t)f3(t)000]T

因此,系统的垂向动力学方程为

2.2外载荷激励

对于轨道式大车行走机构,轨道接头不平是影响大车运行安全的主要因素,本文将研究新型大车行走机构匀速通过这类缺陷时的动力学响应.轨道接头激励模型一般分为2类:缝接头激励模型和焊接接头激励模型[6].

2.2.1有缝轨道接头激励数学模型

常见轨道有缝接头模型有2种形式:错牙接头模型和宽轨缝接头模型.

(1) 错牙接头是钢轨接头处两轨面存在高低偏差的一种接头形式.根据大车行驶方向的不同,可将错牙类型分为迎轮错牙和顺轮错牙,如图5所示,通常前者对轮轨冲击影响较大[6].

图5 错牙接头Fig.5 Rail joint

大车匀速通过时,根据图5中速度的矢量关系,得到轮系通过轨道迎轮错牙接头时的竖向冲击速度为

同理,轮系通过轨道顺轮错牙接头时的竖向冲击速度为

式中:R为车轮踏面半径(mm);h为错牙高度(mm);v为大车速度(m/s).

(2) 宽轨缝接头激励模型如图6所示,b为轨缝宽度,轮系通过该类接头时的冲击速度为

2.2.2焊接轨道接头激励数学模型

焊缝接头2种常见形式:凸形焊缝接头和凹形焊缝接头.

(1) 凸形焊缝接头

图6 宽轨缝接头Fig.6 Broad rail gap joint

图7为凸形焊接接头示意图,该类接头可以通过谐波形式来模拟,其谐波表达式为[7]

图7 凸形焊接接头Fig.7 Convexity weld joint

(2) 凹形焊缝接头

受焊接工艺、材质等因素影响,钢轨焊接区轨面硬度比钢轨母材低.在车轮的长久冲击下,钢轨焊接区轨面将出现下凹的塑性变形,形成凹形焊接接头.同样,通过谐波形式来模拟此类接头,其谐波表达式为

大车机构匀速经过有缝接头时,其激励模型可以视为车轮垂向的速度激励,经过焊缝接头时可以视为车轮垂向的位移激励.在求解过程中,将激励转化为等效力施加于3个车轮上.

2.3系统主要参数

2.3.1轮轨接触刚度的确定

轮轨作用力用Hertz非线性弹性接触理论确定[8]:

式中:轮轨接触常数G=3.86R-0.115×10-8m/N3/2;车轮踏面半径R=315 mm;u0(t)为轮轨间弹性压缩量,根据该式,可得到如图8虚线所示轮轨接触力与接触变形曲线.由于轮轨接触力与接触变形为非线性关系,为便于计算,利用三段线性函数拟合轮轨间接触力与接触变形间的近似线性关系,图8中实线所示即为线性拟合结果.

图8 轮轨接触力与轮轨间压缩量关系曲线Fig.8The relationship between wheel railcontact force and compression

拟合结果如下:当接触变形为0～0.1 mm时,f0(t)=9.93×108u0(t);当接触变形为0.1～0.2 mm时,f0(t)=1.95×109u0(t)+9.93×104;当接触变形大于0.2 mm时，f0(t)=2.83×109u0(t)+4.89×105.

由于车轮受到轨道的支反力,车轮系零部件间的间隙逐渐受到挤压,轮系间隙约为δ0=0.2 mm.因此,求解各轮系与轨道间的刚度时,应当考虑该间隙的削弱作用,即在轮轨间接触变形的基础上加上轮系各部件间的间隙,求出在总变形下的刚度值.经计算,得到上述接触变形范围下的刚度分别为

k0i=3.31×108N/m

k0i=9.75×108N/m

k0i=1.89×109N/m

2.3.2车架与轮系2接触刚度的确定

在有限元分析软件Ansys中建立模型,对相应自由度位置加载单位力,找出相应点的位移,然后计算得到刚度.当轮系2向车架作用单位力时,则可由轮系2竖直方向位移计算得到轮系2与车架间的刚度值.在车架与轮系2接触处施加单位力时,车架竖直方向的位移云图如图9所示.

图9 车架竖直方向位移云图Fig.9 The vertical displacement nephogram of frame

根据云图显示结果可知,车架与轮系2接触位置的位移约x02=0.84×10-6mm,于是,接触刚度为

k2=1/x02=1.2×109N/m

同理,应用该方法可获得其他部分刚度值.

2.3.3各部分阻尼的确定

由于阻尼具体数值难以确定,故利用实模态解法,首先建立系统无阻尼振动方程,待方程解耦后，通过模态阻尼比得到系统阻尼矩阵,将阻尼矩阵列入振动方程,从而建立有阻尼振动方程.一般机械结构的阻尼比约为5%[9].

3 动力学响应分析

通过对质量矩阵及刚度矩阵正则化,得到主质量矩阵和主刚度矩阵,利用临界模态阻尼比得到主阻尼矩阵[9],最后在Matlab中利用状态空间法求解系统动力学响应.

3.1迎轮错牙接头激励下的轮轨动力学响应

根据《桥式和门式起重机制造及轨道安装公差》(GB/T 10183—2005)中规定,轨道接头高低偏差不应大于1.0 mm[10].参考该标准,对大车行走机构匀速通过高度偏差分别为1.0及2.0 mm的迎轮错牙接头进行仿真,轮轨垂向力瞬态响应曲线分别如图10和图11所示.

从图10和图11中可以看出,每个轮系受到激励作用时,车轮产生较大的瞬时冲击力,且偏差越大,瞬时冲击越剧烈,随后作用力在约几ms的时间内迅速衰减.另外,由于车架的传递作用,将使其他轮系处车轮与轨道间也产生一定的冲击,但冲击力明显小于受激励轮系处的轮轨冲击;3个车轮均通过接头后,在系统阻尼的作用下,各轮系与轨道间的轮轨冲击力逐渐衰减至稳定值并趋于一致,其稳定值约为250 kN,即起重机匀速行驶时的车轮轮压.

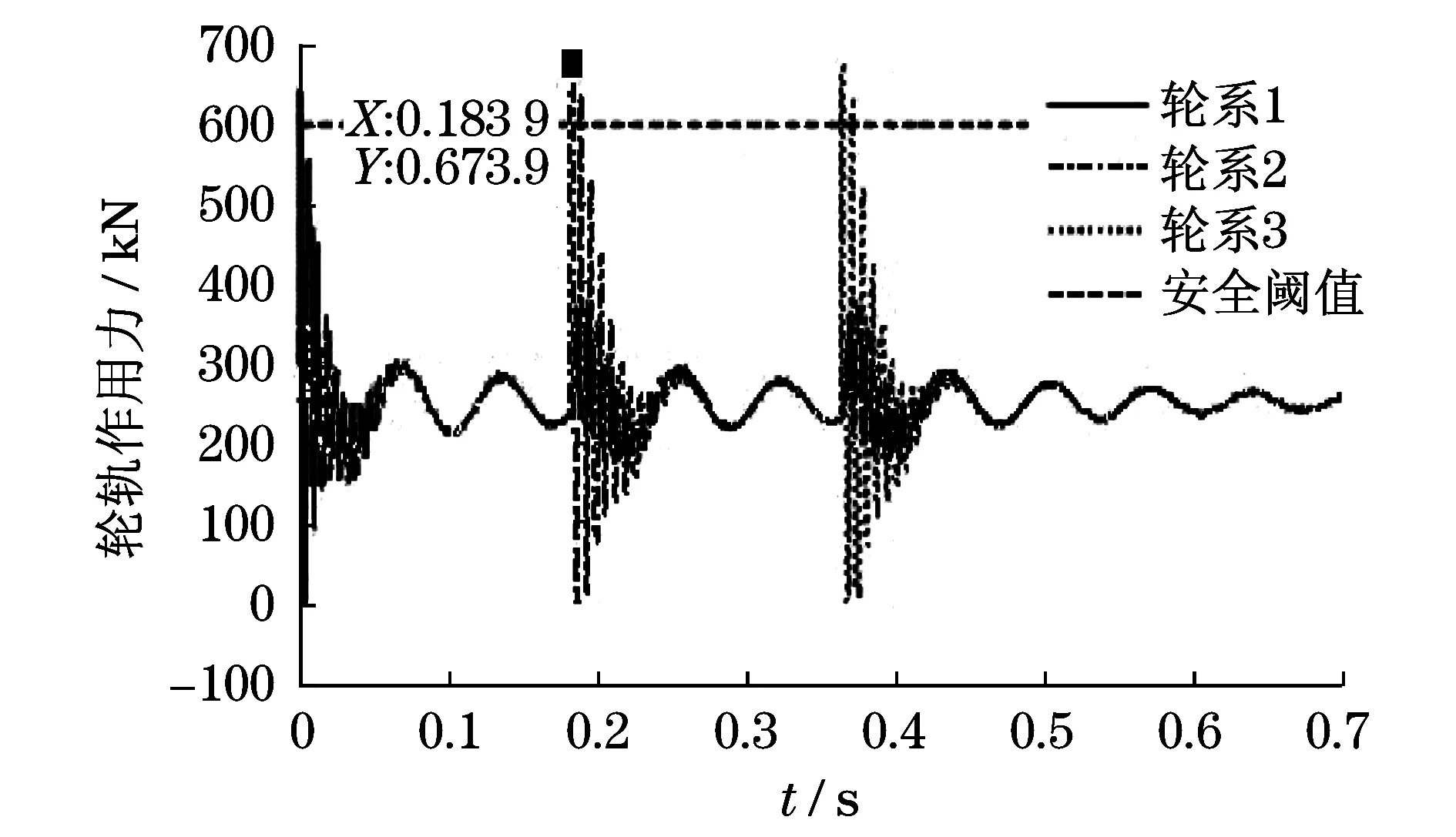
图10 迎轮错牙高度差为1.0 mm时的轮轨动力学响应曲线Fig.10Wheel rail dynamic response curve when theheight of inverse rail joint is 1.0 mm

图11 迎轮错牙高度差为2.0 mm时的轮轨动力学响应曲线Fig.11Wheel rail dynamic response curve when theheight of inverse rail joint is 2.0 mm

3.2顺轮错牙接头激励下的轮轨动力学响应

对大车行走机构匀速通过高度偏差分别为2.0,2.5 mm的顺轮错牙接头进行仿真,轮轨瞬态作用力响应曲线分别如图12和图13所示.

图12 顺轮错牙高度差为2.0 mm时的轮轨动力学响应曲线Fig.12Wheel rail dynamic response curve whenthe height of positive rail joint is 2.0 mm

图13顺轮错牙高度差为2.5 mm时的轮轨动力学响应曲线Fig.13Wheel rail dynamic response curve whenthe height of positive rail joint is 2.5 mm

对图12和图13的响应曲线进行分析,发现其特征与大车匀速通过轨道迎轮错牙接头时相同,所不同的是错牙高度差相同时的各轮系处瞬时冲击力均小于前者,这与实际情况相符.

3.3宽轨缝接头激励下的轮轨动力学响应

《桥式和门式起重机制造与轨道安装公差》中规定,轨道接头间隙不大于2.0 mm.参考该标准,对宽缝宽度分别为2.0,10.0 mm时进行仿真,响应曲线如图14和图15所示.

图14 宽轨缝宽度为2.0 mm时轮轨动力学响应曲线Fig.14Wheel rail dynamic response curvewhen the gap is 2.0 mm

图15 宽轨缝宽度为10.0 mm时轮轨动力学响应曲线Fig.15Wheel rail dynamic response curvewhen the gap is 10.0 mm

由仿真结果可知：轨缝宽度为2.0 mm时,三车轮在接头处轮轨冲击力最大为252.8 kN;轨缝宽度为10.0 mm时,三车轮在接头处轮轨冲击力最大值均约为358 kN,远小于错牙激励的峰值,可见轮轨冲击力对于宽轨缝缺陷并不敏感.

3.4凸形焊缝接头激励下的轮轨动力学响应

类比某重载铁路焊缝实测数据,焊接接头缺陷波长约为0.1～0.2 m,焊接处凸凹矢度不大于0.3 mm.在我国《铁路线路修理规则》中指出,1 m直尺范围内,焊缝凸凹矢度超过0.5 mm,应进行整治.

由于波长越短,焊缝处表面变化越剧烈,轮轨冲击力也越大.因此选择对波长为0.1 m时,波高为0.5和1.0 mm的焊缝激励进行仿真,结果如图16和图17所示.

3.5凹形焊缝接头激励下的轮轨动力学响应

选择对波长为0.1 m时,波深为0.5和1.0 mm的凹形焊缝激励进行仿真,结果如图18和图19所示.

图16波高0.5 mm的凸形焊缝接头激励下的动力学响应曲线Fig.16Wheel rail dynamic response curve when theheight of convexity weld joint is 0.5 mm

图17波高1.0 mm的凸形焊缝接头激励下的动力学响应曲线Fig.17Wheel rail dynamic response curve when theheight of convexity weld joint is 1.0 mm

图18波深0.5 mm的凹形焊缝接头激励下的动力学响应曲线Fig.18Wheel rail dynamic response curve whenthe depth of concavity weld joint is 0.5 mm

由仿真结果可知,焊缝接头激励下的接头处轮轨冲击作用效果较为平缓.

根据规范,设计的轮压安全阈值在800 kN,瞬时冲击力在安全阈值的1.5倍(1 200 kN)以下时,由于作用时间极短,对车轮及轨道的影响不大.车轮在通过轨道接头产生的最大瞬时冲击力汇总如表1所示.

图19波深1.0 mm的凹形焊缝接头激励下的动力学响应曲线Fig.19Wheel rail dynamic response curve whenthe depth of concavity weld joint is 1.0 mm表1 车轮瞬时冲击力最大值Tab.1 Maximum value of instantaneous wheel impact force

轨道缺陷类型偏差/mm最大冲击力/kN迎轮错牙接头1．0673．92．0871．2顺轮错牙接头2．0746．92．5834．8宽轨缝接头2．0252．710．0358．0凸形焊缝接头0．5337．41．0441．1凹形焊缝接头0．5364．51．0479．0

由表1可知:

(1) 缺陷偏差越大,轮轨作用越强烈,对整机越不利.但三轮系处的轮轨瞬时冲击力均小于轨道允许最大承载1 200 kN,且除瞬时冲击力外,三轮系处稳定轮轨作用力均在安全阈值(800 kN)以下,说明新型三轮大车机构能够较好地适应轨道缺陷,满足轨道承载设计规范的要求.

(2) 对于有缝接头,大车通过迎轮错牙接头时,轮轨之间冲击作用最大,是最为敏感的轨道缺陷,因此轨道制造和铺设中应严格控制错牙接头的高度差;对于宽轨缝接头缺陷,轮轨响应并不敏感;对于焊接接头,由于焊接接头轨道表面变化平缓,轮轨间冲击力比有缝接头要小.因此,实际使用中应尽量选用焊接接头的轨道.

4 虚拟样机仿真验证

为验证动力学模型和方程的正确性,通过ADAMS虚拟样机仿真与上述数值计算结果进行对比,分析两者的一致程度.由于大车行走机构对迎轮错牙接头缺陷最为敏感,这里将分析该缺陷下的动力学响应.

在ADAMS中建立虚拟样机模型后,在对模型施加材料、约束、接触力等命令后,得到仿真模型如图20所示.ADAMS做动力学仿真计算时,零件间接触刚度越大,积分求解越困难.ADAMS中钢材间的接触刚度一般定义为1.0×108N/m,而前面计算得到的轮轨及其他零部件间接触刚度达到1.0×109N/m以上.为获得较高的求解精度和便于比较分析,取数值分析模型中的各部分接触刚度均为1.0×108N/m,同时,也取大车虚拟样机模型中的轮轨接触刚度为1.0×108N/m.

图20 新型轨道式三轮大车行走机构ADAMS仿真模型Fig.20The model of rail mounted three-wheeledgantry in ADAMS

4.1车架位移响应结果对比

图21为迎轮错牙高度差为1 mm时,车架位移响应的ADAMS动力学仿真结果与理论分析结果对比图.由于大车三车轮依次通过错牙接头,因此,大车位移呈阶梯状增加1 mm,其位移变化趋势符合实际情况.同时,两仿真结果的相位、幅值和变化趋势基本一致.

图21 车架位移响应仿真结果对比Fig.21The comparison between displacementresponses of vehicle frame

4.2轮系3处轮轨作用力结果对比

图22为迎轮错牙高度差为1 mm时,轮系3处轮轨动力学响应的ADAMS动力学仿真结果与本章力学方程仿真结果对比图.易于看出,两仿真结果趋势是基本一致的.

图22 轮系3处轮轨动力学响应仿真结果对比Fig.22The comparison between wheel raildynamic responses of train 3

综上,ADAMS动力学仿真结果与动力学方程分析结果拟合度较高,说明理论分析模型与ADAMS虚拟样机模型具有一定的可比性,验证了前文动力学模型的正确性.

5 结论

本文提出了一种新型轨道式三轮大车行走机构设计方案,并建立了轮轨垂向耦合动力学模型,分析了在迎轮错牙接头、顺轮错牙接头、宽轨缝接头、凸形焊缝接头和凹形焊缝接头这5种轨道常见缺陷激励下的动力学响应.为验证动力学模型的正确性,利用ADAMS对方案进行对比仿真,研究结论如下:

(1) 结构优化后的新型轨道式三轮大车行走机构具有良好的轮轨动力学特性,降低大车高度,能够较好地适应各种轨道缺陷;

(2) 利用ADAMS模型仿真的结果与利用动力学模型求解的响应结果具有一定的可比性,验证了轮轨耦合动力学模型的正确性和高效性;

(3) 错牙接头缺陷是最为敏感的轨道缺陷,且在实际使用中,应优先选用焊接接头的轨道.

[1] 朱德金,王桂梅.门座起重机大车运行机构平衡梁加工工艺的改进[J].起重运输机械,2006(11):70.

ZHU D J,WANG J M.Improvement of processing technology of gantry crane’s blancing beam[J].Port Machineries,2006(11):70.

[2] 杨宇华,张氢,聂飞龙.集装箱自动化码头发展趋势分析[J].中国工程机械学报,2015(6):571-576.

YANG Y H,ZHANG Q,NIE F L.Trend analysis on automated container terminals[J].Chinese Journal of Construction Machinery,2015(6):571-576.

[3] 李维玲,沈超.2000 t门式起重机走行机构的设计研究[J].建筑机械,2014(1):103-106.

LI W L,SHEN C.Design on running mechanism of the 2000 t gantry crane[J].Construction Machinery,2014(1):103-106.

[4] 李谷音,常红.港口起重机械[M].北京:人民交通出版社,2009.

LI G Y,CHANG H.Port machineries[M].Beijing:China Communications Press,2009.

[5] 颜鸿森.机械装置的创造性设计[M].北京:机械工业出版社,2002:69-137.

YAN H S.Creative design of mechanical device[M].Beijing:China Machine Press,2002:69-137.

[6] 翟婉明.车辆—轨道耦合动力学[M].北京:科学出版社,2007.

ZHAI W M.Vehicle-track coupling dynamics[M].Beijing:Science Press,2007.

[7] 王慎.重载铁路钢轨焊缝不平顺区域的轮轨动力作用及其安全阈值分析[D].成都:西南交通大学,2014.

WANG S.Wheel-rail interaction due to rail weld irregularity and its safety threshold in heavy haul railway[D].Chengdu:Southwest Jiaotong University,2014.

[8] 金学松,刘启跃.轮轨摩擦学[M].北京:中国铁道出版社,2004.

JING X S,LIU Q Y.Wheel-rail tribology[M].Beijing:China Railway Press,2004.

[9] OGATA K.System dynamics[M].Beijing:China Machine Press,2004.

[10] GB/T 10183—2005,桥式和门式起重机制造与轨道安装公差[S].

GB/T 10183—2005,The manufacture of bridge and gantry crane with track installing tolerances[S].

Wheel-raildynamicanalysisofanewrailmountedthree-wheeledgantry

ZHANGQing,CHENMiao,SUNFeng,QINXianrong,SUNYuantao

(School of Mechanical Engineering,Tongji University,Shanghai 201804, China)

Wheel-rail dynamic response between rail mounted gantry and rail becomes worse in view of the transport demand increases severely,affecting the service life of parts and rail seriously.This paper proposes a new rail mounted three-wheeled gantry which replaces the original balance beam structure with frame and balancing-linkage mechanism to reduce RMG height and enhance its dynamic performance.To verify the rationality of the new structure design,gantry’s dynamic equation is established based on Lagrange dynamics method,and the wheel-rail vertical dynamic response is calculated under the three typical types of rail defects,these are rail joint,broad rail gap joint and weld joint.Dynamic simulation in ADAMS is conducted to verify the calculated results further.The results show that the correctness and rationality of the dynamic model of wheel-rail,the new rail mounted three-wheel gantry has good dynamic performance,and the height of the gantry could be effectively reduced.

wheel-rail vertical force; wheel-rail contact stiffness; dynamic model; rail joints

TH 213.5

A

1672-5581(2017)04-0329-09