变分模态分解和熵理论在超声信号降噪中的应用

杜必强,孙立江,2

(1.华北电力大学 能源动力与机械工程学院,河北 保定071003; 2.中国航发北京航科发动机控制系统科技有限公司,北京102200)

中央高校基本科研业务费资助项目(2014MS118)

杜必强(1974—),男,副教授,博士.E-mail:ncepudu@gmail.com

变分模态分解和熵理论在超声信号降噪中的应用

杜必强1,孙立江1,2

(1.华北电力大学 能源动力与机械工程学院,河北 保定071003; 2.中国航发北京航科发动机控制系统科技有限公司,北京102200)

针对超声检测信号中结构噪声难以去除的问题,提出了一种变分模态分解(Variational Mode Decomposition,VMD)和小波能量熵阈值(Wavelet Energy Entropy Threshold,WEET)联合降噪的算法.分析了含噪系统熵增的特性以及结构噪声在不同时间段的分布特征,提出了用小波能量熵表征信号的含噪状态,并以小波能量熵最大子区间的小波系数参与计算各个尺度层的阈值.对仿真及实测信号进行处理,结果表明,该方法(VMD-WEET)能很好地抑制超声回波信号中存在的白噪声及结构噪声,还原了准确的波形特征,验证了其有效性.

超声检测; 降噪; 变分模态分解; 小波能量熵

在现场超声检测中,技术人员通常根据回波信号来判断被检测对象是否存在缺陷.作为一种典型的非线性、非平稳信号,回波信号本身含有许多突变成分,包含了大量的有用信息,但超声波在材料晶粒散射引起的结构噪声以及采集仪器的散射噪声，都会使回波信号包含大量噪声,严重干扰了有用信号特征的提取,影响检测结果.因此,采用有效的信号处理方法，抑制回波信号携带的各种噪声,提高信噪比,有利于下一步对缺陷回波信号的特征提取和模式识别.

近年来,小波分析和经验模态分解(Empirical Mode Decomposition,EMD)因其良好的时频分析能力而广泛应用于超声信号处理领域.周西峰等[1]针对传统一代小波会把信号当成噪声滤除的不足,提出了基于提升小波变换的超声信号降噪算法,取得了一定的效果.向东阳等[2]通过理论分析证明了传统小波变换系数相关去噪方法的不足,重新定义了相关系数,提出了改进相关系数的去噪算法,仿真信号处理结果表明,该算法能更好地去除噪声并保留信号的边缘信息,但缺乏实际信号的验证.李秋峰等[3]采用EMD对粗晶材料超声检测信号消噪方法进行了研究,通过分析IMF分量及其频谱，筛选出了部分有用分量进行重构,一定程度上增强了回波信号.张樯等[4]提出了一种改进的EMD阈值消噪算法,根据自相关系数的特点,找到模态的分界点,分别采用不同的阈值对噪声含量不同的信号进行处理,取得了较好的效果.但是,在小波阈值消噪算法中,阈值的选择难以根据信号本身的特点自适应的选取是该算法的最大瑕疵之处,一直以来,都无法找到令人满意的最优阈值选择方法.而EMD算法至今仍存在缺乏严格的数学基础和模态混叠等关键性的问题.另外,还有部分学者提出了广义K-奇异值分解和匹配追踪算法[5-6]，试图来解决超声信号消噪这一特定的工程问题.但是,以上学者均未充分考虑超声检测信号所包含噪声的特性.

针对上述问题,笔者分析了超声回波信号所包含噪声的类型,建立了超声回波信号及其噪声模型;尝试引入变分模态分解(Variational Mode Decomposition,VMD)算法及用熵理论分析改进的小波阈值算法,对超声回波信号进行消噪处理;将处理结果与传统的小波软阈值消噪算法、EMD阈值消噪算法进行对比.结果表明:经该算法消噪后的波形平滑、失真度小,有很好的工程应用前景.

1 超声回波信号模型及其噪声特性分析

超声回波信号是超声入射波遇到缺陷反射回来的信号.通常情况下,超声回波信号的数学模型[7-8]可以表示为

f(t)=Aexp[-α(t-τ)2]cos[ωc(t-τ)+φ]

(1)

式中:A为回波信号的幅值;α为带宽因子;ωc为回波信号的中心频率;τ和φ分别为缺陷回波信号返回的时间和相位.

超声回波信号主要包含2种噪声[9]:① 材料晶粒散射引起的结构噪声;② 采集仪器的电噪声.一般认为采集仪器的电噪声是白噪声,在整个观测时域内服从正态分布,与缺陷回波信号是不相关的.而材料晶粒散射引起的结构噪声,可以看作多个晶粒散射的超声波叠加在一起的结果,在时域上和回波信号存在着强相关,而在频域上和回波信号频谱重叠.通常情况下,不考虑各晶粒间超声波的多次散射,材料晶粒散射引起的结构噪声可以表示为

(2)

式中:Y为超声探测声束范围内的晶粒数;Ai为各晶粒散射回波的幅值;DF为衰减因子;b为大于零的常数;ωc为超声缺陷回波信号的中心频率;ωi为结构噪声对入射波频率的漂移;τi为各晶粒散射回波返回的时间;ωi和τi为整个观测时域内服从均匀分布的随机数.

2 基于VMD和小波能量熵阈值降噪算法

2.1VMD基本原理

VMD作为一种新的自适应信号处理方法,由Dragomiretskiy等[10]于2014年提出.它将信号分解过程转移到变分框架内,通过搜寻约束变分模型最优解来实现信号的自适应分解.假设每个模态是具有中心频率的有限带宽,约束变分模型为

(3)

式中:k为分解后得到的模态个数;uk和ωk分别为分解各个模态的时域信号和中心频率.

为求解上述约束变分模型的最优解,引入了二次惩罚因子α和Lagrange乘子λ(t),将约束变分问题转化为非约束变分问题,其中二次惩罚因子可以显著降低高斯噪声的影响,而Lagrange乘子则能使约束条件保持严格性,则增广的Lagrange函数为

(4)

利用Lagrange法的交替方向乘子求解变分问题式(4)的最优解,从而将原始信号自适应的分解为K个BIMF分量,具体实现过程如下:

(2)n=n+1,执行整个循环;

(4)k=k+1,重复步骤(3),直到k=K,结束内层第1个循环;

(6)k=k+1,重复步骤(5),直到k=K,结束内层第2个循环;

2.2VMD参数确定及消噪原理

VMD算法需要事先设定分解层数K和惩罚因子α.研究表明:模态分量个数多少的设定关乎VMD方法分解的性能.K选择偏大时,就会出现过分解现象,即同一频率或尺度的信号被分解到不同的模态分量中;K选择偏小时,就会出现欠分解现象,即同一个模态分量中出现了不同频率或尺度的信号.因此,只要K值选择合理,就可以有效地避免分解信号产生模态混叠.理论上,经VMD分解得到的BIMF分量是按低频到高频分布的,当最后一个BIMF分量的中心频率首次取到最大值时,分解层数是最优的.因此,本文采用观察中心频率法[11]确定分解层数K,惩罚因子α则选取默认值2 000.

通常我们认为采集仪器的电噪声表现为高频成分,和缺陷回波信号相关性较小.因此,利用上述方法确定分解层数K,对含噪的回波信号进行VMD分解,分解后得到从低频到高频分布的K个BIMF分量,计算各个分量与回波信号的相关系数,剔除相关系数较小的BIMF分量.经过这样消噪处理以后,回波信号所含噪声主要为材料晶界散射引起的结构噪声.而这种噪声通常和回波信号在部分时间-尺度上是相关的,一般消噪算法难以将结构噪声和回波信号进行最优分离.

为了消除材料晶界散射引起的结构噪声,对重构后的信号进行小波分解.考虑到结构噪声在不同时间段的分布特征,利用小波分析良好的局部特性[12],在某个局部时间段内找出结构噪声最集中的区域.估计该区域小波系数的噪声方差,用于Donoho阈值的计算上,这样选取的阈值对结构噪声有很好的滤波效果.因此,关键的问题在于如何找出结构噪声分布最集中的区域.

2.3信息熵理论

为了找到结构噪声最集中的区域,需要以某个指标表征噪声的大小.为此,引入信息熵表征系统的含噪状态.信息熵[13]是用来描述序列的复杂性的统计指标,其大小反映序列概率分布的均匀性.熵值越大,序列分布越随机;反之,序列越确定.

(5)

式中:MX为变量的X的信息熵,当pi=0,piIni=0.

(6)

对比式(5)和式(6),可以看出,含噪系统出现熵增现象,即系统的无序成分增加.

由以上分析可知,含噪系统会出现熵增.也就是说,在噪声最集中的区域,熵值最大.并且信号经小波分解,随着分解层数的增加,噪声的能量会迅速衰减.因此,可以用小波能量熵表征系统的含噪状态.

2.4小波能量熵阈值选取方法

对目标信号进行j尺度的小波分解,把得到每个尺度的细节部分当成一个独立的信号进行处理.根据时间特性,将每个尺度层上的细节部分等分成s个子区间,则每个子区间有N/s个采样点数,其中第i个子区间的细节部分系数对应的能量为

(7)

第j层细节部分系数的总能量为

(8)

第i个子区间所包含的信号能量占该尺度层总能量的概率为

Pi=Ei/Ej

(9)

则第i个子区间的小波能量熵为

(10)

由前述分析可知,小波能量熵值最大子区间是噪声最集中的区域,此时,可以认为该子区间的小波系数是由噪声引起的.因此,计算每个尺度层细节部分的各个子区间的小波能量熵,将小波能量熵最大子区间的细节系数的平均值作为各尺度层的噪声方差,然后利用Donoho[14]提出的公式来计算各个尺度层上的阈值:

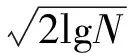
(11)

式中:δj为分解尺度j上的噪声方差,此时计算的阈值也是根据结构噪声在各尺度层的能量特征自适应选取的.

2.5超声波信号消噪方法

VMD-WEET消噪算法具体步骤如下:

(1) 确定目标信号的分解层数K,对其进行VMD分解,得到从低频到高频分布的K个BIMF分量,计算各个分量与原信号的相关系数,剔除相关系数较小的BIMF分量,重构剩余分量;

(2) 选择小波基函数sym8,对重构信号进行j尺度小波分解,得到各尺度下的近似部分和细节部分;

(3) 对各尺度下的细节部分进行小波能量熵阈值算法降噪,得到消除结构噪声后的细节系数;

(4) 用第j层的近似系数和经消噪处理后的细节系数重构信号.

3 仿真和试验

3.1仿真信号试验

根据式(1)和式(2)分别得到回波信号、结构噪声,然后在回波信号中添加结构噪声及白噪声,得到染噪回波信号.仿真回波信号和染噪回波信号的时域图如图1所示.分别对仿真回波信号和染噪信号做频谱,如图2所示,可以看到,仿真回波信号和噪声不仅在时域上混叠,还在频域上混叠.这说明了部分噪声和仿真回波信号在某个尺度上是相关的.

根据2.2节所述的观测中心频率法确定VMD的分解模态数K,表1中列出了不同K值下各模态的中心频率.当K=4时,出现了相近的频率,认为是过分解现象.因此选用K=3,α则选用VMD默认值2 000,分解结果如图3所示.

相关系数是用来表征两个变量间相关程度的统计指标.一般来说,采集仪器散射噪声(白噪声)和缺陷回波信号相关性较小.因此,可以通过计算VMD分解后的各个模态和原信号的相关系数,以剔除相关系数较小的分量(认为是采集仪器散射噪声).经过大量计算,本文阈值λ设定为0.1,即相关系数小于0.1的分量,就被认为是采集仪器的散射噪声而剔除.表2列出了3个模态分量与原信号的相关系数.其中u3和原信号的相关系数很小,认为是采集仪器的散射噪声而剔除.重构剩余两个分量,由图4可以看出,重构后的信号仍含有噪声,这种噪声是结构噪声.用前述的小波能量熵阈值算法对重构信号进行处理,得到消噪后的信号.可以看到,噪声得到了很好的抑制.

图1 仿真测试信号Fig.1 Simulation test signals

图2 仿真测试信号频谱Fig.2 The spectrum of simulation test signals表1 仿真信号不同K值下的归一化中心频率Tab.1Normalized center frequency of differentK-values from simulation test signals

模态数K中心频率归一化20．09950．4517——30．09010．44390．6805—40．09010．11890．44410．6830

图3 仿真信号VMD分解结果Fig.3VMD decomposition result ofsimulation test signals表2 仿真信号下各模态与原信号的相关系数Tab.2The correlation coefficient for each modeemulation signal with the original signalof simulation test signals

模态u1u2u3相关系数0．81110．49570．0013

图4 结构噪声去除前后的信号对比Fig.4Signal contrast before and afterstructural noise removal

为了证明本文所提出方法的有效性,将文中方法与EMD阈值消噪算法、小波软阈值消噪算法进行对比.经3种算法处理染噪信号后的时域波形及频谱图分别如图5和图6所示,其中小波软阈值消噪算法的小波基函数选择sym8,分解层数为4层.可以看到,EMD阈值消噪算法和小波软阈值消噪算法并没有很好地去除材料晶粒散射引起的结构噪声.而本文所提方法去除了大部分噪声,还原了波形的平滑度,表现出了很好的效果.

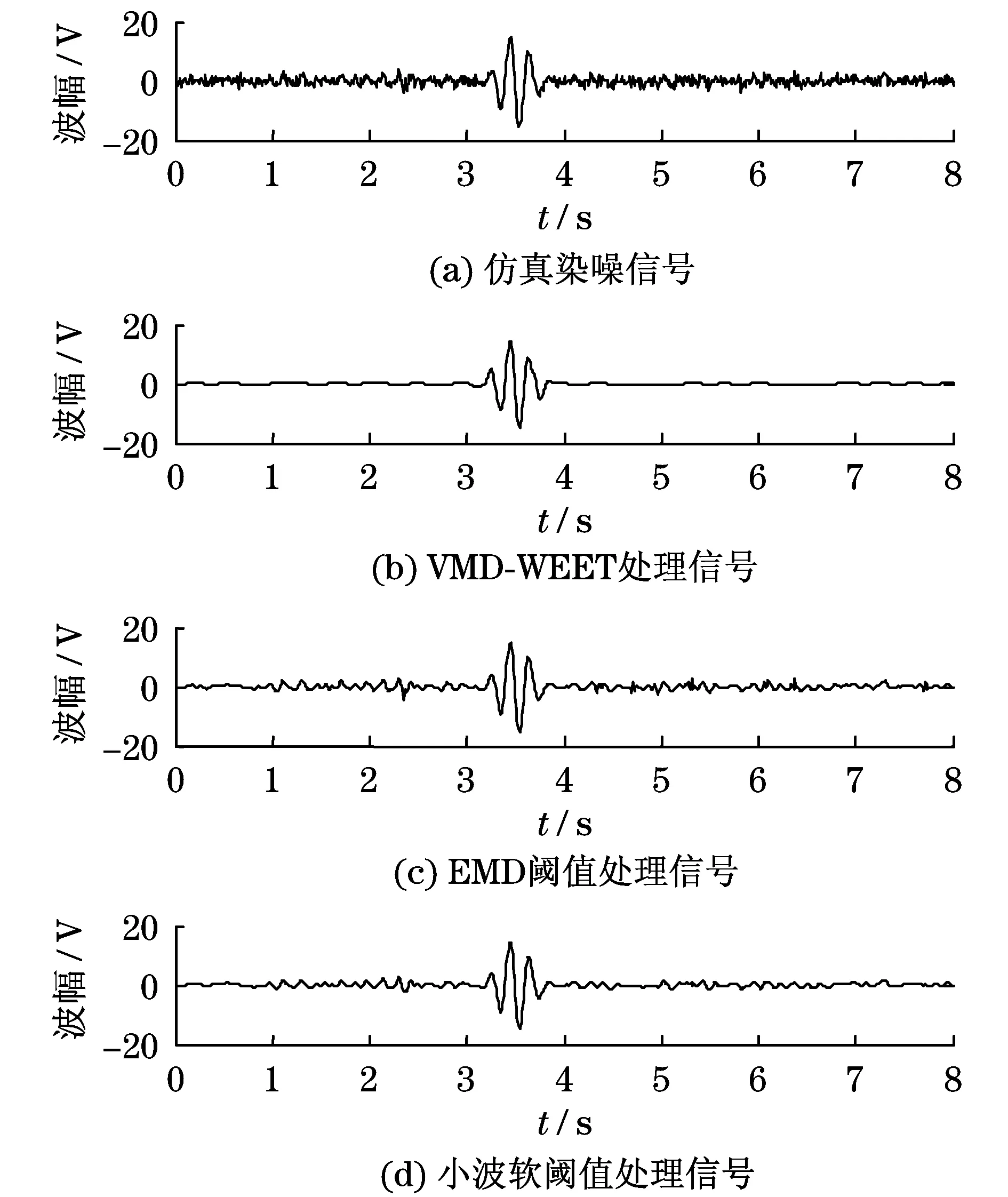
图5 仿真信号处理方法对比Fig.5Processing method comparisonof simulation signals

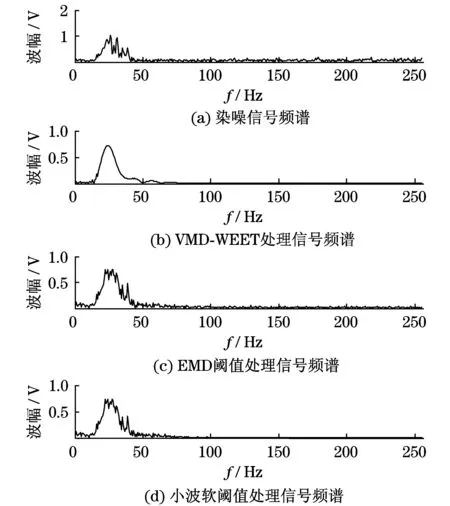
图6 仿真信号频谱图对比Fig.6 Spectrum comparison of simulation signals

3.2降噪效果评价

衡量信号降噪效果的指标通常有信噪比(SNR)、均方根误差(RMSE)和相似系数(NCC),其定义如下:

(12)

(13)

(14)

式中;X(n)为原始含噪信号;S(n)降噪后信号;N为信号长度.

对3种方法所处理信号进行降噪效果评价,如表3所示列出了3种方法降噪前后信号的SNR,RMSE和NCC,本文所提出方法降噪指标最优,这反映了该方法的有效性.

表3 SNR,RMSE和NCC的不同降噪方法比较结果Tab.3Results of different de-noising methodson SNR,RMSE and NCC

3.3实测信号试验

在实验室搭建一套信号采集系统.信号采集系统包括超声相控阵检测仪、中心频率为2.5 MHz的探头和计算机.采集到的实测信号如图7所示,该信号含有严重的噪声,会对后续的特征提取产生影响.因此,利用本文所述消噪方法对信号进行预先处理.

图7 实测回波信号Fig.7 Real echo signal

根据2.2节所述的观测中心频率法确定VMD的分解模态数K,表4中列出了不同K值下各模态的中心频率.当K=7时,出现了两个比较相近的频率,认为是出现了过分解.因此,选用K=6.分解结果如图8所示,并计算各模态与原信号的相关系数,列于表5中.

由表5可以看到,模态6和原信号的相关系数小于阈值0.1,因此,认为模态6主要是采集仪器散射的噪声引起的.重构前5个模态信号,进行小波能量熵阈值消噪,将消噪结果与EMD阈值消噪算法、小波软阈值消噪算法进行对比,如图9和图10所示.EMD阈值消噪算法和小波软阈值消噪算法并没有很好地去除噪声,这是因为实测信号中,材料晶粒散射引起的结构噪声较多,用传统的消噪算法难以有效地将这种噪声去除.而本文所提方法对这种结构噪声和白噪声都有很好的滤波效果.

表4 实测信号不同K值下的归一化中心频率Tab.4 Normalized center frequency of different K-values from real echo signal

表5 实测信号各模态与原信号的相关系数Tab.5 The correlation coefficient for each mode emulation signal with the original signal of real echo signal

图8 实测信号VMD分解结果Fig.8 VMD decomposition result of real echo signal

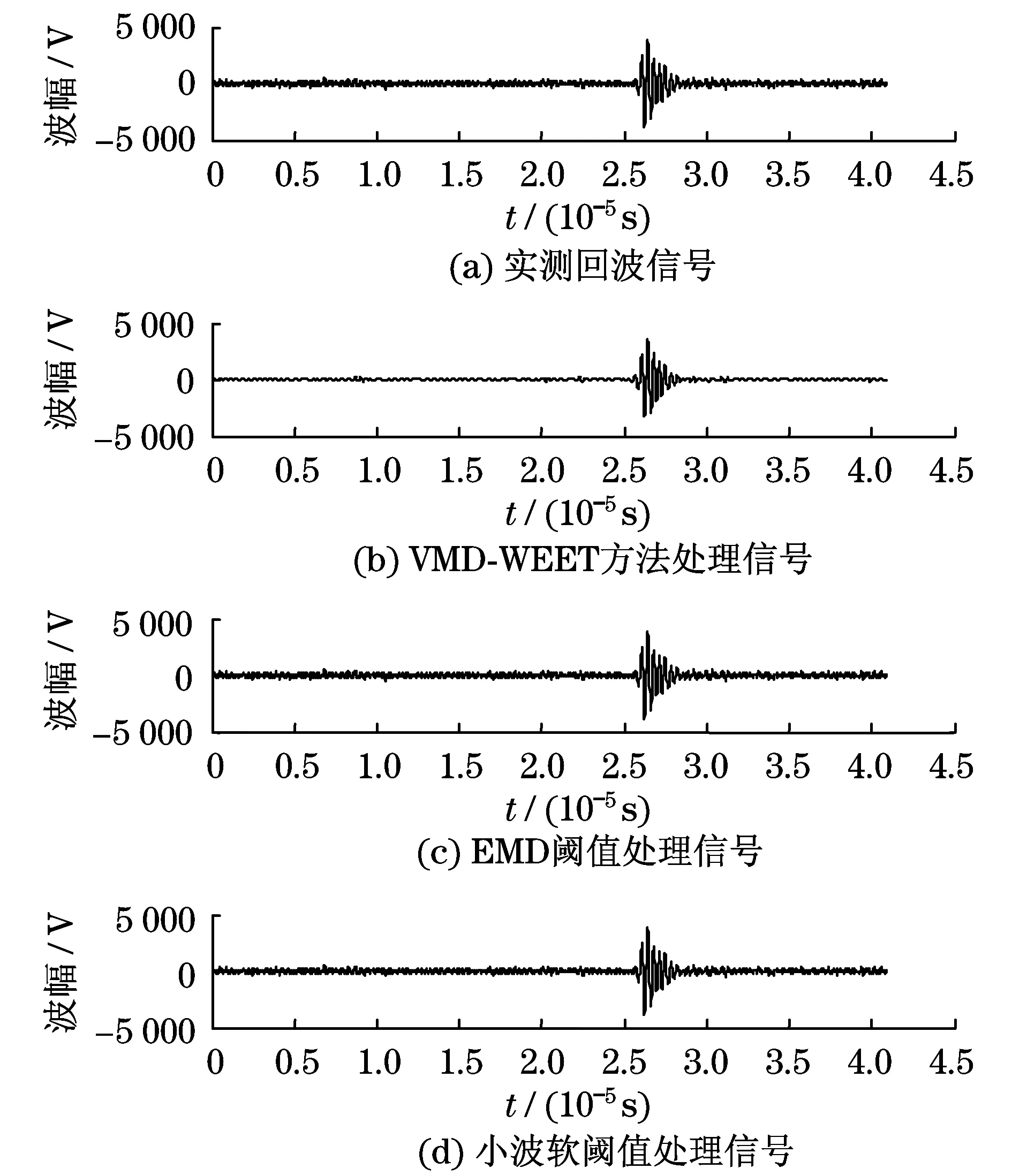
图9 实测信号处理方法对比Fig.9 Processing method comparison of real echo signal

4 结论

引入了新的自适应信号处理方法——变分模态分解,克服了EMD缺乏严格的数学基础和模态混叠等关键性的问题,对采集仪器散射噪声有很好的滤波效果.针对材料晶粒散射引起的结构噪声,分析了含噪系统的熵增特性,用熵表征系统的含噪状态,将小波能量熵最大子区间的细节部分系数的平均值作为Donoho阈值的噪声方差,这样选取的阈值对结构噪声有很好地去除效果.

图10 实测信号频谱图对比Fig.10 Spectrum comparison of real echo signal

[1] 周西峰,肖武,郭前岗.基于提升小波的超声信号降噪方法[J].探测与控制学报,2012,34(4):43-46.

ZHOU X F,XIAO W,GUO Q G.Ultrasonic signal de-noising based on lifting wavelet[J].Journal of Detection & Control,2012,34(4):43-46.

[2] 向东阳,吴正国,胡文彪,等.改进的小波变换系数相关去噪方法[J].振动、测试与诊断,2010,30(5):561-565.

XIANG D Y,WU Z G,HU W B,et al.Improved de-noising algorithm using correlation of wavelet coefficient[J].Journal of Vibration,Measurement & Diagnosis,2010,30(5):561-565.

[3] 李秋锋,黄攀,施倩,等.基于经验模态分解去噪的粗晶材料超声检测[J].应用基础与工程科学学报,2014,22(3):566-573.

LI Q F,HUANG P,SHI Q,et al.Based on EMD de-noising coarse grain materials ultrasonic testing[J].Journal of Basic Science and Engineering,2014,22(3):566-573.

[4] 张樯,周西峰,王瑾,等.基于改进的EMD超声信号降噪方法研究[J].南京邮电大学学报(自然科学版),2016,36(2):49-55.

ZHANG Q,ZHOU X F,WANG J,et al.Ultrasonic signal de-noising based on improved EMD[J].Journal of Nanjing University of Posts and Telecommunications(Natural Science Edition),2016,36(2):49-55.

[5] 魏东,周健鹏.K-SVD和OMP算法在超声信号去噪中的应用[J].应用声学,2016,35(2):95-101.

WEI D,ZHOU J P.Application of K-SVD and OMP algorithm on ultrasonic signal de-noising[J].Applied Acoustics,2016,35(2):95-101.

[6] 何明格,殷鹰,林丽君,等.基于小波迹和匹配追踪算法的超声波检测信号消噪[J].应用基础与工程科学学报,2011,19(2):297-304.

HE M G,YIN Y,LIN L J,et al.De-noising of ultrasonic testing signal based on wavelet foot print and matching pursuit[J].Journal of Basic Science and Engineering,2011,19(2):297-304.

[7] CARDOSO G,SANIIE J.Data compression and noise suppression of ultrasonic NDE signals using wavelets[C]// Ultrasonics,2003 IEEE Symposium on,IEEE.2003:250-253.

[8] SANIIE J,WANG T,BILGUTAY N M.Analysis of homomorphic processing for ultrasonic grain signal characterization[J].IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control,1989,36(3):365-375.

[9] 闫晓玲,董世运,刘彬,等.基于熵理论的超声波检测信号消噪与缺陷识别[J].北京理工大学学报,2012,32(5):465-469.

YAN X L,DONG S Y,LIU B,et al.De-noising of ultrasonic signals based on entropy theory and recognition of defect in material[J].Journal of Beijing Institute of Technology,2012,32(5):465-469.

[10] DRAGOMIRETSKIY K,ZOSSO D.Variational mode decomposition[J].IEEE Transactions on Signal Processing,2014,62(3):531-544.

[11] 刘长良,武英杰,甄成刚.基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J].中国电机工程学报,2015,35(13):3358-3365.

LIU C L,WU Y J,ZHEN C G.Rolling bearing fault diagnosis based on variational mode decomposition and fuzzy C means clustering[J].Proceedings of the CSEE,2015,35(13):3358-3365.

[12] 李书,陈益.超声探测弱信号提取方法[J].振动、测试与诊断,2006,26(1):33-36.

LI S,CHEN Y.Study on weak signal extraction in ultrasonic detection[J].Journal of Vibration,Measurement & Diagnosis,2006,26(1):33-36.

[13] 潘宏侠,都衡,马春茂.局域波信息熵在高速自动机故障诊断中的应用[J].振动、测试与诊断,2015,35(6):1159-1164.

PAN H X,DU H,MA C M.High-speed automation fault diagnosis based on local wave and information entropy[J].Journal of Vibration,Measurement & Diagnosis,2015,35(6):1159-1164.

[14] 张培林,李一宁,徐超,等.润滑油磨粒超声回波信号的双树复小波自适应降噪[J].北京理工大学学报,2015,35(9):908-912.

ZHANG P L,LI Y N,XU C,et al.The adaptive de-noising based on dual-tree complex wavelet transform for uitrasonic echo signal of wear debris in lubricant oil[J].Journal of Beijing Institute of Technology,2015,35(9):908-912.

Applicationofvariationalmodedecompositionandentropytheoryinultrasonicsignalde-noising

DUBiqiang1,SUNLijiang1,2

(1.School of Energy,Power and Mechanical Engineering,North China Electric Power University,Baoding 071003,Hebei,China; 2.Aero Engine Corporation of China Beijing Aerospace Engine Control System Technology Co.,Ltd.,Beijing 102200,China)

Aiming at the problem of difficult to remove the structural noise in ultrasonic testing signals,this paper presented a de-noising method which combined variational mode decomposition(VMD)and wavelet energy entropy threshold (WEET).Firstly,the characteristic of entropy increase in noisy system and the distribution feature of structural noise in different period were analyzed.Then,the state of signal with noise was characterized by wavelet energy entropy and the threshold of wavelet decomposed in different scales ware determined according to the wavelet energy entropy.Simulation and experimental results show that the de-noising method(VMD-WEET)in this paper can restrain the noise and restore the accurate waveform to verify its effectiveness.

ultrasonic inspection; de-noising; variational mode decomposition; wavelet energy entropy

TH 17

A

1672-5581(2017)04-0310-08