加速度计的离心加速度场翻滚校准方法

廖建平，尹晓丽，李晓婷

（中航工业北京长城计量测试技术研究所，北京 100095）

加速度计的离心加速度场翻滚校准方法

廖建平，尹晓丽，李晓婷

（中航工业北京长城计量测试技术研究所，北京 100095）

针对现有加速度计校准方法的不足，提出了一种在大于 1g的离心大加速度激励下加速度计的多位置翻滚校准方法。建立了加速度计在离心加速度场翻滚校准的数学模型，研究了加速度计的离心加速度场翻滚校准方法，给出了离心加速度场翻滚校准步骤，并采用石英加速度计进行了离心加速度场的十二位置等多位置翻滚校准试验，获得了大g值激励下加速度计的安装误差、交叉耦合系数等模型方程系数。采用本方法进行校准，校准状态更接近加速度计实际使用状态，因而校准获得的模型方程系数用于修正后，将提高加速度计的测量精度。

加速度计；双离心机；离心加速度场；翻滚校准

若采用现有的加速度计重力场翻滚校准法、精密离心机校准法，加速度计的安装误差、交叉耦合系数等模型方程系数只能在1g（g为重力加速度）的加速度激励下校准获得，无法在离心大加速度激励下校准获得。而加速度计用于测量大加速度时，通常仍采用在重力场校准获得的模型方程系数。这种将重力场校准获得的模型方程系数用在大加速度测量中的方式，势必会带来较大的加速度测量误差。针对该问题，本文提出了一种在大于 1g的离心加速度场下加速度计的多位置翻滚校准方法。

1 加速度计概述

加速度计是用来测量比力的一种传感器。加速度计的坐标系由输入基准轴 IA、摆基准轴 ΡA、输出基准轴OA组成，用右手定则确定，表示为

加速度计的模型方程是表达加速度计的输出与沿加速度计输入基准轴IA作用的加速度等物理量之间数学关系的方程式。加速度计简化的模型方程可表示为：

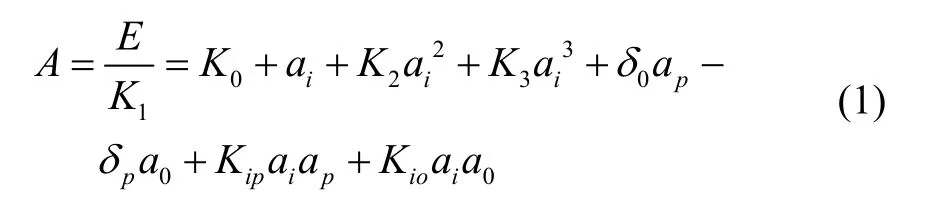
在使用加速度计之前，必需对其进行校准以获得其偏值、标度因数、安装误差等模型方程系数，并将这些模型方程系数带入式(1)中进行修正，才能获得准确的加速度测量结果。

2 现行的加速度计校准方法

目前加速度计的校准方法主要有重力场翻滚校准法和精密离心机校准法。

重力场翻滚校准法是以当地重力加速度为标准值，通过分度装置对重力加速度进行分度，产生-1g～+1g范围内的多个加速度点，通过校准获得-1g～+1g范围内的模型方程系数，包括偏值、标度因数、二阶非线性系数、安装误差、交叉耦合系数。精密离心机校准法是控制离心机产生一系列的大g值加速度，通过校准获得大g值下加速度计的模型方程系数，包括偏值、标度因数、二阶非线性系数、三阶非线性系数等。

现行校准方法的局限性：加速度计的安装误差、交叉耦合系数只能在重力场校准获得，无法在大于1g的离心加速度下校准获得，但在加速度计的实际应用中，却采用重力场校准结果进行加速度计全量程模型修正，这种用法必然会带来较大的加速度测量误差。对此，本文提出了一种基于双离心机的加速度计离心加速度场翻滚校准方法，以获得离心大g值下加速度计的安装误差、交叉耦合系数等模型方程系数，从而可提高加速度测量精度。

3 离心加速度场翻滚校准建模

3.1 双离心机的原理及组成

如图1所示，在主离心机的转盘上安装从离心机，主离心机和从离心机的旋转轴互相平行，且都垂直于水平面。主离心机旋转中心为O1，从离心机旋转中心为O2，从离心机坐标系为O2-xyz。主离心机的工作半径为（即线段O1O2），主离心机转速为，离心加速度指向x轴正向。

通过控制主离心机旋转，在从离心机的旋转中心O2处产生的离心加速度为

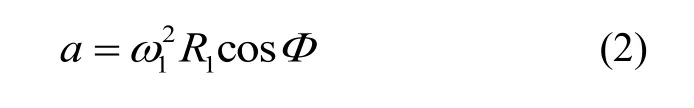
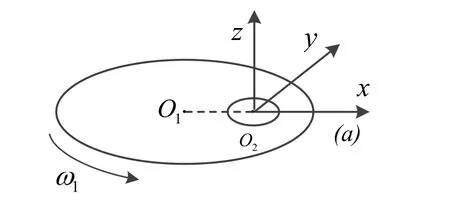
图1 双离心机原理图Fig.1 Principle of the double centrifuges

3.2 离心加速度场翻滚校准建模

摆式加速度计的安装方式分为摆态和门态两种，本文介绍摆态安装方式的离心加速度场翻滚校准。

图2 离心加速度在各轴的分量Fig.2 Centrifugal acceleration’s component along each axis

如图2所示，若加速度计坐标系原点与从离心机坐标系原点O2重合，加速度计输出基准轴OA与z轴重合，输入基准轴IA与-y的夹角为θ，则离心加速度在加速度计各轴的分量为

主离心机稳速旋转，则加速度幅值保持不变。从θ=0°开始，控制从离心机顺时针依次转过30°，即0°、30°、60°、… 、270°、300°、330°共十二个位置，每个位置加速度计的输出分别记为E0+、E1+、E2+、…… E9+、E10+、E11+。顺时针旋转从离心机至360°位置，再从θ=330°开始，依次逆时针转过30°，即330°、300°、270°、…、60°、30°、0°共十二个位置，每个位置加速度计的输出分别记为 E11-、E10-、E9-、…、E2-、E1-、E0-。取每个角位置点顺时针、逆时针两次加速度计输出数据的平均值作为该角位置点加速度计的输出值，从而得到加速度计在十二位置的输出值分别为E0、E1、E2、…、E9、E10、E11。

将加速度计的输出值，带入加速度计模型方程式(1)，并展开为如下傅氏级数：

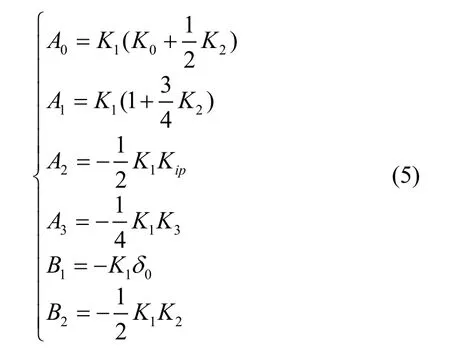
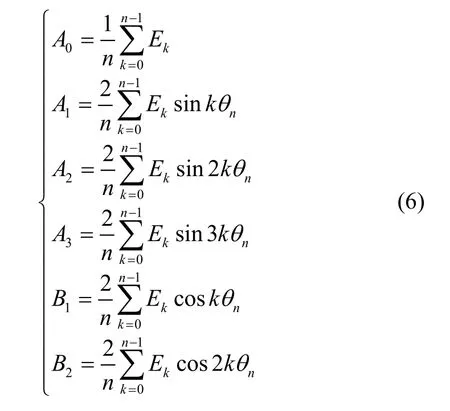
因此，加速度计模型方程系数的最佳估计值为：

由此得到摆态安装下，加速度计十二位置翻滚校准的模型方程系数分别为：

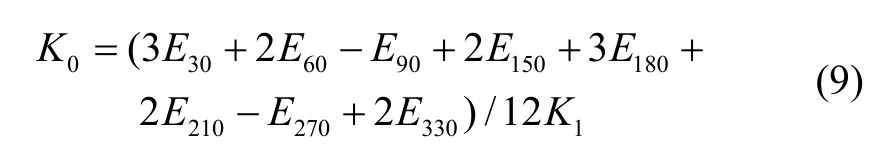
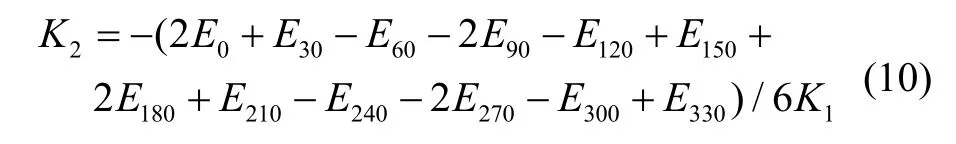
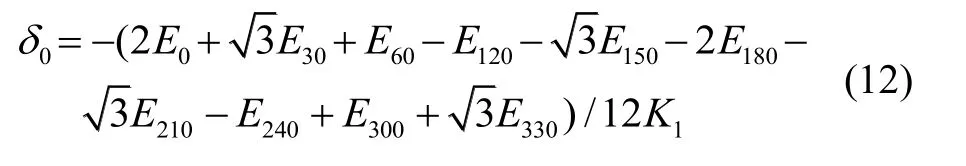
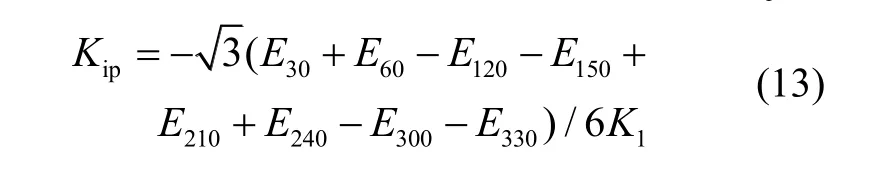
4 离心加速度场翻滚校准方法

在加速度计的离心加速度场翻滚校准前，需调整使得主离心机工作面、从离心机工作面与水平面的夹角都满足要求（一般要求小于±20″）。加速度计的离心加速度场翻滚校准方法，包括质心调整、初始零位角确定、主离心机工作半径反算、翻滚校准等操作步骤，见图3所示。

图3 加速度计的离心加速度场翻滚校准步骤Fig.3 Procedure of tumbling calibration for accelerometer in centrifugal acceleration field

下面介绍其中的加速度计检测质量质心调整、初始零位角确定和主离心机工作半径确定方法。

4.1 调整使得加速度计质心重合

加速度计安装到从离心机上后，设其检测质量的质心在安装面上的投影与从离心机旋转中心 O2之间的距离为从离心机静止时，加速度计输出记为V0；控制从离心机以转速匀速旋转，加速度计的输出记为E。则质心偏差

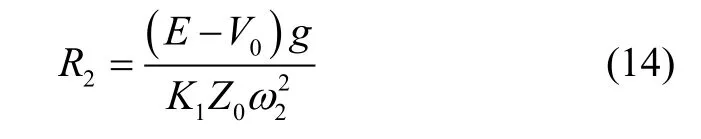
4.2 确定初始零位角

初始零位角是指加速度计处于摆态0°角位置，此时加速度计输入轴IA方向与离心加速度方向垂直，即离心加速度在加速度计输入轴IA上的分量为零。确定初始零位的方法通常有两种：光学测量法和基于模型的计算法。光学测量法需要搭建测量光路系统，再采用“光电自准直仪+反射镜”等方法确定初始零位角；基于模型的计算法依靠被测加速度计的输出，通过加速度计的输出来确定其初始零位角。本项目中采用基于模型的计算法。

如图4所示，在从离心机坐标系O2-xyz中，设加速度计输入轴IA与-y方向的夹角为，并锁紧从离心机。测量加速度计的输出，并记为V0。

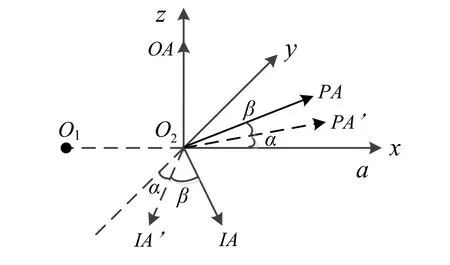
图4 初始零位角确定原理Fig.4 Principle for determining the initial zero angle

旋转主离心机，使其输出加速度为a（5g左右），测量加速度计的输出，记为V1，则有：

联立以上两式，推导得：

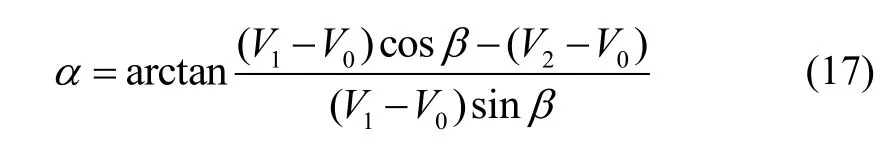
4.3 确定主离心机工作半径

主离心机工作半径的确定采用半径反算法，即通过测量加速度计的输出反算主离心机工作半径。

利用加速度计在重力场校准获得的零偏 K0、标度因数K1，分别计算得到摆态90°位置时的工作半径R1-和摆态270°位置时的工作半径R1+为：

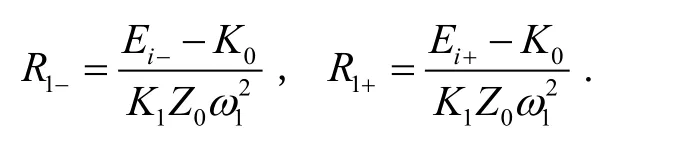
由此得到主离心机工作半径R1为：

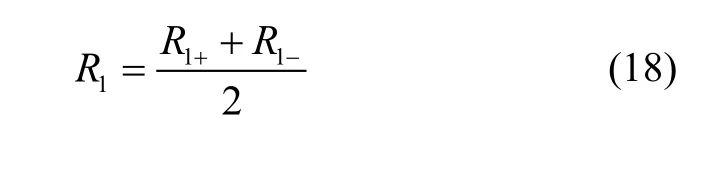
5 校准试验及数据分析

5.1 校准试验

采用我单位已有的双离心机，分别对悬丝支撑摆式、石英挠性摆式加速度计进行了校准试验。双离心机实物图见图 5，某型石英加速度计在从离心机上的安装见图6。

1）不同离心加速度下十二位置翻滚校准试验

用编号为 0105-192的石英加速度计，在 1～20g范围内选择9个不同的加速度点，分别进行了离心下十二位置翻滚校准试验，试验数据见表1。

2）四位置、八位置、十二位置离心下翻滚校准试验

图5 双离心机实物图Fig.5 The picture of double centrifuges

图6 石英加速度计的安装图Fig.6 The installation of quartz accelerometer

用编号为0105-192的石英加速度计，在1～20g范围内选择5个不同的加速度点，分别进行了四位置、八位置、十二位置的离心下翻滚校准试验，并分别获得了加速度计的模型方程系数的校准结果，其中 K0的校准结果见图 7，K1的校准结果见图 8，K2的校准结果见图9，安装误差的校准结果见图10。

由图7知，随着加速度增大，四位置、八位置和十二位置校准获得的偏值K0绝对值呈增大趋势。

由图8知，随着加速度增大，四位置校准获得的标度因数K1的变化量不大，八位置和十二位置校准获得的K1都变大，且增大趋势一致。

由图9知，随着加速度增大，四位置校准获得的二阶非线性系数K2基本不变，八位置和十二位置校准获得的K2都变大，且增大趋势基本一致。

由图10知，随着加速度值增大，四位置、八位置和十二位置校准获得的摆态安装误差 δ0绝对值都增大，且增大趋势一致。

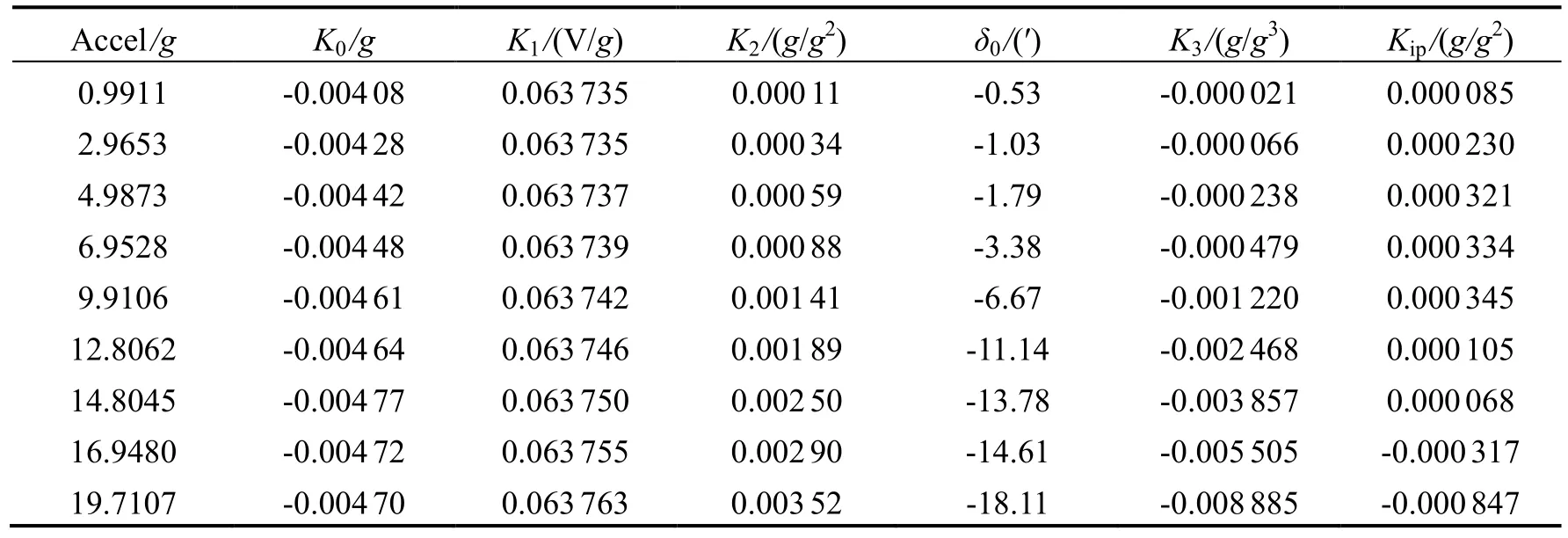
表1 不同离心加速度下十二位置翻滚校准数据Tab.1 12-position tumbling calibration data in different centrifugal accelerations

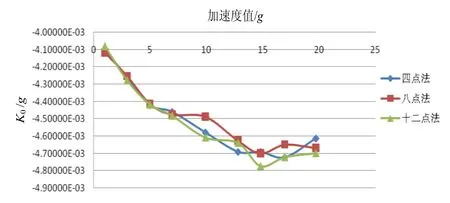
图7 不同校准方法下K0的对比Fig.7 Comparison of K0 under different calibration methods

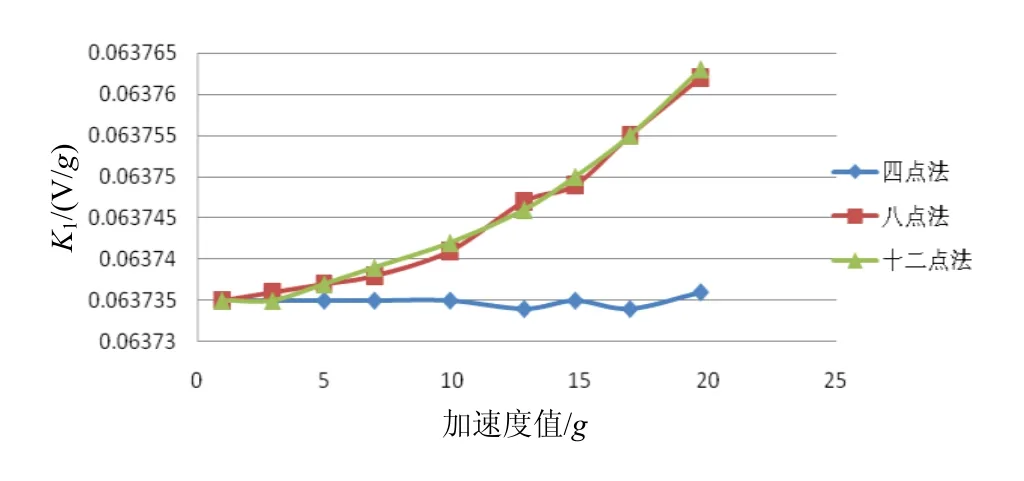
图8 不同校准方法下K1的对比Fig.8 Comparison of K1 under different calibration methods

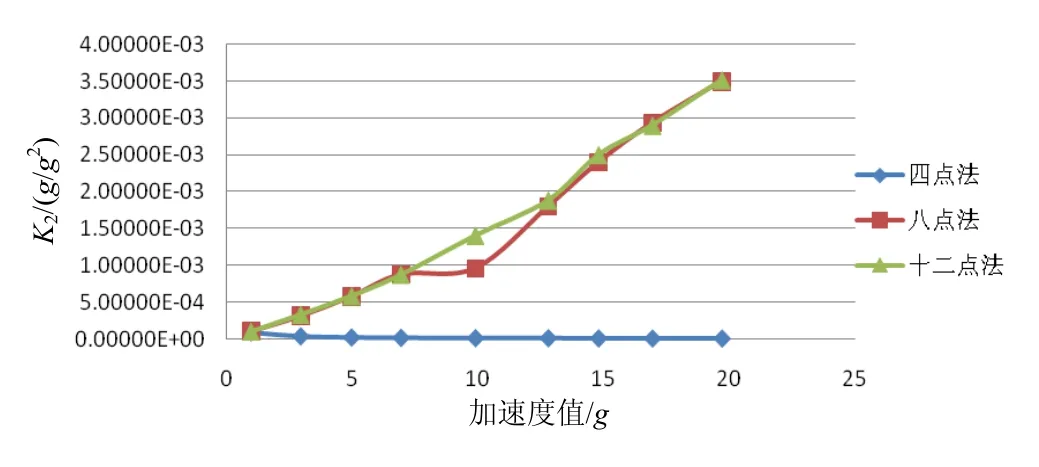
图9 不同校准方法下K2的对比Fig.9 Comparison of K2 under different calibration methods

图10 不同校准方法下δ0的对比Fig.10 Comparison of δ0 under different calibration methods

5.2 试验数据分析

通过对加速度计离心加速度场翻滚校准试验的数据进行比较分析，得出如下结论：

1）离心加速度增大时，用四位置、八位置和十二位置校准获得的偏值K0、安装误差δ0的绝对值都逐渐增大；

2）离心加速度增大时，用八位置和十二位置校准获得的标度因数 K1、二阶非线性系数 K2都增大，但四位置校准获得的K1、K2都基本不变；

3）加速度计在离心下翻滚校准试验中，八位置和十二位置的校准结果基本一致，四位置校准结果与这两者有差异，分析认为四位置校准无法分离出高次项系数，K1、K2结果中包含了高次项系数的影响。

因此进行加速度计的离心加速度场翻滚校准，宜采用八位置翻滚或十二位置翻滚法。

6 结 论

本文提出了一种加速度计在大于 1g的离心加速度场下多位置翻滚校准方法，该方法可在大加速度下校准获得加速度计偏值K0、标度因数K1、安装误差、交叉耦合系数等模型方程系数。该方法在大于 1g的大加速度激励下校准，校准状态更接近加速度计实际使用状态，校准获得的模型方程系数更为准确可靠，进行模型修正后将提高加速度计的测量精度。

（References）：

[1]廖建平, 龙祖洪, 徐永, 等. 基于双离心机的正弦加速度数学模型的建立[J]. 中国惯性技术学报, 2007, 15(2):252-254.Liao Jian-ping, Long Zu-hong, Xu Yong. Sine acceleration model based on double centrifuge[J]. Journal of Chinese Inertial Technology, 2007, 15(2): 252-254.

[2]鲁金瑞, 任顺清, 王常虹. 振动整流法辨识加速度计非线性误差模型系数[J]. 仪器仪表学报, 2013, 34(9):2130-2136.Lu Jin-rui, Ren Shun-qing, Wang Chang-hong. Identification method of accelerometer nonlinear error model coefficients with vibration rectification[J]. Chinese Journal of Scientific Instrument, 2013, 34(9): 2130-2136.

[3]IEEE Std 836-2009. IEEE Recommended Practice for Precision Centrifuge Testing of Linear Accelerometers[S].IEEE-SA Standards Board, 2009.

[4]IEEE 1293-1998. IEEE Standard Specification Format Guide and Test Procedure for Linear, Single-Axis, Nongyroscopic Accelerometers[S]. IEEE-SA Standards Board,1998.

[5]王世明, 王翌, 伊国兴, 等. 精密离心机的惯性组合加速度计的参数标定方法[J]. 中国惯性技术学报, 2013,21(2): 264-270.Wang Shi-ming, Wang Yi, Yi Guo-xing, Calibration of accelerometers fixed in SINS on precision centrifuge[J].Journal of Chinese Inertial Technology, 2013, 21(2): 264-270.

[6]汤莉, 王雷, 孟慧丽, 等. 石英加速度计重力场试验定位基准问题与解决方案[J]. 航天控制, 2013, 31(2): 89-93.Tan Li, Wang Lei, Meng Hui-li, Orientation and solution of quartz accelerometer test on gravity field[J]. Aerospace Control, 2013, 31(2): 89-93.

[7]IEEE Std 1554-2005. IEEE Recommended Practice for Inertial Sensor Test Equipment, Instrumentation, Data Acquisition, and Analysis[S]. IEEE Aerospace and Electronic Systems Society, 2005.

[8]Nicklich H, Mende M. Calibration of very low frequency accelerometers - A challenging task[J]. Sound and Vibration, 2011, 45(5): 1521-1527.

[9]Wu Yun-long, Li Hui, Zou Zheng-bo. External calibration of GOCE data using regional terrestrial gravity data[J]. Geodesy and Geodynamics, 2012, 3(3): 34-39.

[10]Huang Jing-qing, Zhao Meng, Zhang Ting-ting. Linearity analysis of closed-loop capacitive accelerometer due to distance mismatch between plates and the influence of compensation capacitor array[J]. Science China Information Sciences, 2014, 57(6): 1-12.Zhang Yong-ping, He Chang-de, Yu Jia-qi. An integrated MEMS piezoresistive tri-axis accelerometer[J]. Journal of Semiconductors, 2013, 34(10): 104009(1-8).

Tumbling calibration method for accelerometer in centrifugal acceleration field

LIAO Jian-ping, YIN Xiao-li, LI Xiao-ting
(Changcheng Institute of Metrology & Measurement of Aviation Industrial Company, Beijing 100095, China)

Aiming at the shortcomings of the existing accelerometer calibration methods, a multi-position tumbling calibration method of accelerometer under the centrifugal acceleration of ＞1g is proposed. First, the mathematical model of accelerometer tumbling calibration in centrifugal acceleration field is established.Then, the method of tumbling calibration in centrifugal acceleration field of accelerometer is studied, and the step of tumbling calibration in centrifugal acceleration field is given. At last, a quartz accelerometer is used to implement multi-position (including 12-position) tumbling calibration tests in the centrifugal acceleration field, and the accelerometer’s model equation coefficients of installation error, cross-coupling coefficient, etc.under a large g value excitation are obtained. The calibration state with the proposed method is more close to the actual using state of the accelerometer, and the model equation coefficient obtained by calibration can be used to correct the measurement accuracy of the accelerometer after it is calibrated by centrifugal acceleration.

accelerometer; double centrifuges; centrifugal acceleration field; tumbling calibration

1005-6734(2017)04-0550-05

10.13695/j.cnki.12-1222/o3.2017.04.022

2017-04-16；

2017-07-10

航空科学基金资助项目（2014ZD44006）

廖建平（1977—），男，高级工程师，从事惯性器件及系统校准技术研究。E-mail: cimmed2000@sina.com

U666.1

A