航天器终端接近的有限时间输入饱和避碰控制

李学辉，宋申民，陈海涛，郭 永

（1. 哈尔滨工业大学 控制理论与制导技术研究中心，哈尔滨 150001；2. 西北工业大学 自动化学院，西安 710000）

航天器终端接近的有限时间输入饱和避碰控制

李学辉1，宋申民1，陈海涛1，郭 永2

（1. 哈尔滨工业大学 控制理论与制导技术研究中心，哈尔滨 150001；2. 西北工业大学 自动化学院，西安 710000）

针对航天器终端接近问题，解决了追踪航天器在跟踪到达期望目标点的过程中不与目标航天器发生碰撞的难题。首先，在目标航天器轨道系下建立了航天器的相对运动和避碰模型。其次，考虑外界扰动上界已知和未知两种情形，均给出了有限时间避碰控制器，且所设计的控制器都具有输入饱和特性。最后，应用 Lyapunov稳定性理论证明了在所提出的控制器作用下系统是有限时间收敛的，并且，利用避碰势函数证明了所设计的控制器能够实现避碰。仿真结果表明，所提出的控制器是有效的。

终端接近；避碰控制；有限时间控制；输入饱和

航天器终端接近技术在航天在轨任务中有重要应用[1-3]。为使追踪航天器完成各种在轨服务任务，要求追踪航天器跟踪到达指定期望位置，当到达期望位置后，由追踪航天器的捕获机构捕获目标航天器。

在追踪航天器接近期望位置过程中，为了航天任务的顺利完成，要求追踪航天器避免与目标航天器发生碰撞。为了解决避障问题，文献[4]基于视线相对运动模型，利用模糊控制，研究了非合作自主交会对接的终端接近问题。文献[5]基于椭圆蔓叶线，应用人工势函数制导方法解决了非合作目标航天器自主交会对接与静态障碍物躲避问题。文献[6]利用线性二次模型预测控制研究了具有避障功能的航天器相对运动制导与控制问题。

在实际航天器控制中，执行机构的输出是受限的，忽略了输入饱和问题可能引起控制性能的下降，甚至可以引起系统不稳定。为了解决输入饱和问题，文献[7]针对追踪星径向方向上推进器出现故障的情况，在常值推力下设计了切换控制，使得追踪星沿着指定的轨迹运动，实现了主动避碰。文献[8]利用高斯伪谱法研究了航天器交会对接问题，针对在推进系统输出有界且功率受限以及避免碰撞的约束下，设计了燃料最优的控制器。文献[9]利用安全正不变集(safe positively invariant sets)研究了航天器相对运动的避障问题，通过应用图形搜索算法找到一条安全无碰撞路径并能够满足推力限制。

为了能够快速完成航天任务，有限时间控制在航天控制中得到了重要应用[10-12]。针对有限时间避碰问题，目前大多数文献还没有有效方法。文献[13]针对多水下机器人系统分别研究了有限时间位置一致性和碰撞避免问题，但所提出的考虑避免碰撞问题的协同控制器不能保证系统有限时间收敛。文献[14][15]针对多体 Euler-Lagrange系统，通过基于零空间(null-space-based)行为控制方法，研究了有限时间编队控制策略，但是当处理有障碍物的情况时，系统仍无法实现有限时间收敛。

上述文献虽然对避免碰撞、输入受限、有限时间收敛等问题进行了研究，但是在一些实际航天任务中，需要将多种约束进行同时考虑。为进一步解决考虑碰撞的航天器终端接近问题，本文设计了具有避碰功能的有限时间饱和控制器。相比于上述文献，本文的创新之处在于：①利用双曲正切函数，使所设计的控制器具有输入饱和特性。②通过引入辅助系统，借助有限时间控制，设计的避碰控制器使系统有限时间收敛。③所设计的控制器能够解决系统外部扰动上界已知和未知两种情况。

1 轨道相对运动和避碰模型

由于追踪航天器在到达期望位置的过程中可能与目标航天器发生碰撞，下面分别建立航天器轨道相对运动和避碰模型，并给出本文的控制目标。

1.1 航天器轨道相对运动模型

图1 航天器终端接近系统Fig.1 System of spacecraft terminal approach

假设空间存在一颗运行在椭圆轨道上的目标航天器，追踪航天器从初始位置到达期望位置，其示意图见图1。其中，FI为赤道惯性坐标系其原点oI为地心；xI轴位于赤道平面内，指向春分点；zI轴沿地球自转轴方向，向上为正；yI轴与xI轴和zI轴构成右手直角坐标系。Fo为目标航天器轨道坐标系作为航天器相对运动的参考坐标系，基本平面为目标航天器瞬时轨道平面，坐标原点ot在目标航天器的质心，xo轴沿地心到目标航天器的矢径方向；yo轴在目标航天器轨道平面上，与xo轴垂直，且沿目标航天器运动方向；zo轴与xo轴和yo轴构成右手直角坐标系。tr和rc分别为地心到目标航天器和追踪航天器质心的位置矢量在赤道惯性坐标系FI下的表示。

假定目标航天器不受主动控制力作用，其动力学模型为

追踪航天器的动力学模型为

式(1)(2)中：mt和mc分别为目标航天器和追踪航天器的质量；dt和dc分别为目标航天器和追踪航天器所受到的外部摄动力；uc为作用于追踪航天器的主动控制力；tr和rc分别为地心到目标航天器和追踪航天器的距离，即为地球引力常数。

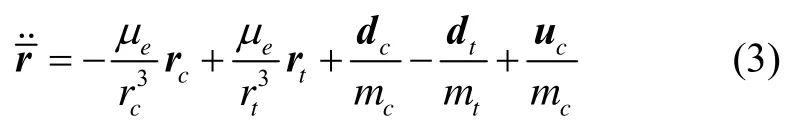
将公式(4)展开，则可得追踪航天器相对于目标航天器的轨道运动方程为[16]

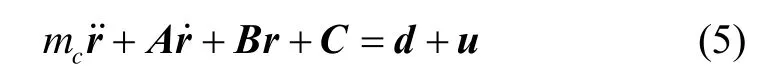
其中，

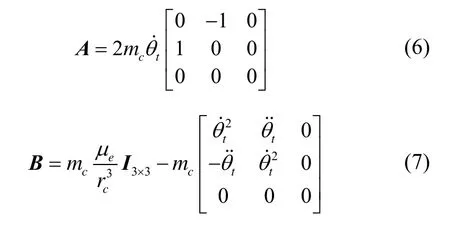
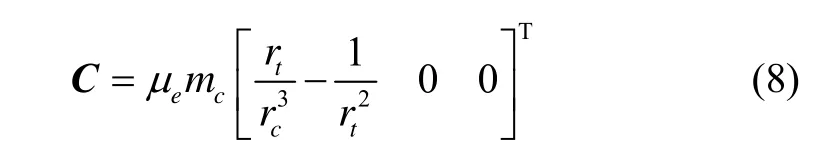
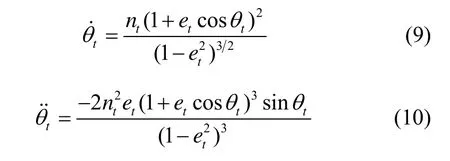
假设追踪航天器的期望位置和速度分别为rd、定义误差向量为重写式(5)，可以得到轨道相对运动学方程为

1.2 避碰模型与控制目标

假设追踪航天器与目标航天器的最小安全距离为a，则以目标航天器质心为原点，半径为a所形成的球为避碰区域。设避碰势函数为

由h(r)的定义可知，当追踪航天器在避碰区域外时h(r)＞0，反之，当追踪航天器在避碰区域内或避碰区域曲面上时

为了控制器的设计和定理的证明，我们给出如下假设。

假设1在初始时刻和期望位置，追踪航天器在避碰区域外，即其中，

注1. 由假设1可知，为了避免追踪航天器进入避碰区域，只需要保证追踪航天器在到达期望位置的过程中h(r)≠0。

假设2系统式(11)外部扰动有界，满足表示向量的2范数，

本文的控制目标：设计有效的具有饱和特性的控制器，使追踪航天器能有限时间到达期望位置，且在接近过程中不会与目标航天器发生碰撞，即误差向量e有限时间收敛到0，并且在收敛过程中h(r)＞0始终成立。

2 有限时间饱和避碰控制器设计

本文利用有限时间控制的思想设计具有饱和特性的航天器终端接近控制器。考虑到航天器在太空环境的复杂性，下面分别对航天器外部扰动上界已知和未知两种情况进行讨论，设计有限时间饱和避碰控制器，以实现控制目标。

2.1 外部扰动上界已知下的避碰控制器设计

追踪航天器在太空中会受到太阳光压、地球重力梯度等扰动的影响。为了处理外部扰动上界已知的情况，下面设计鲁棒的有限时间饱和避碰控制器。

设计控制器(13)和辅助系统(14)(15)：

定理1针对系统(11)，在假设1和2条件下，且系统外部扰动上界dm已知，控制参数满足则在控制器(13)和辅助系统(14)(15)的作用下，可以得到如下结论（若控制参数不满足则所设计的控制器将不能抵消外界扰动对系统的影响，从而可能导致系统是不稳定的）：

1）追踪航天器能够有限时间运动到期望位置rd。

2）追踪航天器在运动过程中不与目标航天器发生碰撞。

3）所设计的控制器具有输入饱和特性。

证明 选取如下Lyapunov函数：

对式(16)求导并将式(11)、控制器(13)和辅助系统(14)(15)代入，可得：

对式(19)求解可得V1满足

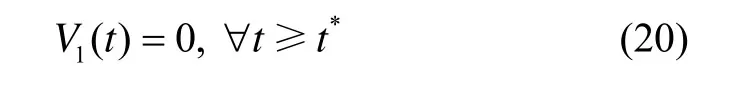
2.2 外部扰动上界未知情况下的避碰控制器设计

由于外部扰动的复杂性，其上界很难精确得到，为了处理外部扰动上界未知的情况，下面设计鲁棒自适应有限时间饱和避碰控制器。

定理2针对系统(11)，在假设1和2条件下，且系统外部扰动上界dm未知，则在控制器(21)和辅助系统(22)～(24)的作用下，定理1的结论仍然成立。

证明 选取如下Lyapunov函数：

对式(25)求导并将式(11)、控制器(21)和辅助系统(22)(23)代入，可得：

利用矩阵A为反对称的性质以及假设2，并将式(24)代入，整理可得：

同定理1的证明，可以证明定理2的结论是成立的。

3 仿真分析

为验证本文控制方法的有效性，下面对所设计的控制器进行仿真验证。假设外界扰动主要考虑J2项引力摄动，设追踪航天器与目标航天器的最小安全距离追踪航天器和目标航天器的质量均为100kg，目标航天器的轨道参数为：其中分别是半长轴、离心率、升交点赤经、轨道倾角、近地点幅角和真近点角。设追踪航天器与目标航天器相对距离和速度的初始值分别为期望相对距离为为了处理当时出现的抖振问题，在时 用来代替

图2 控制器(13)～(15)下控制力曲线图Fig.2 Curves of control force under controller (13)-(15)

针对控制器(13)～(15)的仿真结果如图2和图3所示。图 2为闭环系统的控制力曲线图，可以看出控制力是有界的。图 3给出追踪航天器的运动轨迹，图中球形区域为避碰区域，直线为起始位置与期望位置之间的连线。从图3可以看出，若追踪航天器直线运动到期望位置，必然进入避碰区域，而在所设计的控制器下，追踪航天器能有效避免进入避碰区域，从而能够安全地到达期望位置。

针对控制器(21)～(24)的仿真结果如图4～6所示。图4为闭环系统的控制力曲线图，图5为外部扰动上界的估计值dˆm的曲线图。从图4可以看出，控制力是有界的。图6给出追踪航天器的运动轨迹，图中球形区域为避碰区域，直线为起始位置与期望位置之间的连线。从图6可以看出，若追踪航天器直线运动到期望位置，必然进入避碰区域，而在所设计的控制器下，追踪航天器能有效避免进入避碰区域，从而能够安全地到达期望位置。

图3 控制器(13)～(15)下追踪航天器运动轨迹Fig.3 Curves of chaser spacecraft’s motion trajectory under controller (13)-(15)

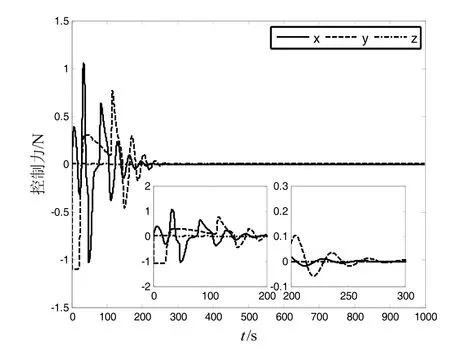
图4 控制器(21)～(24)下控制力曲线图Fig.4 Curves of control force under controller (21)-(24)

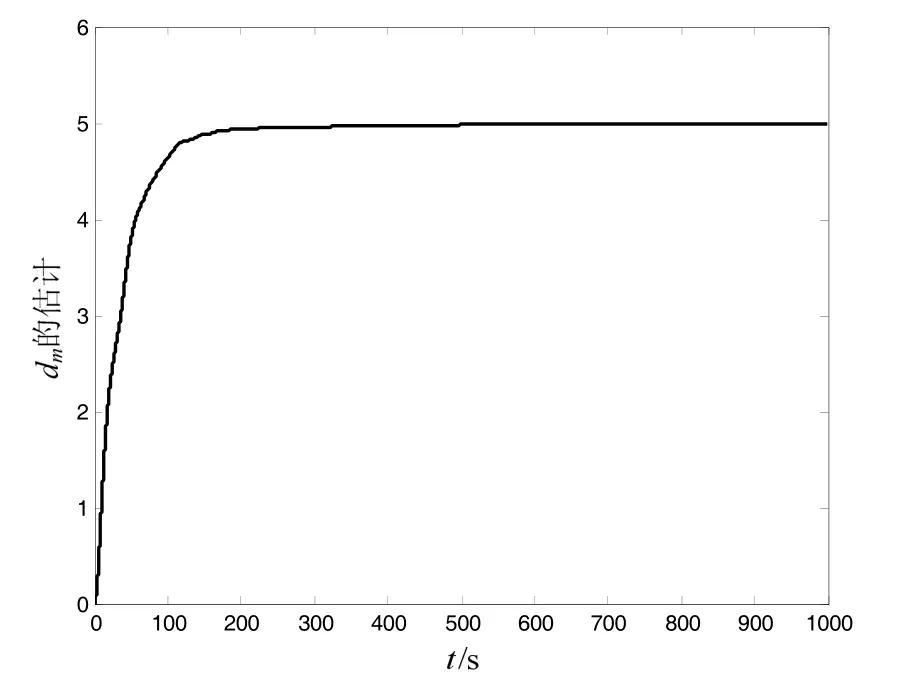
图5 曲线图Fig.5 Curve of

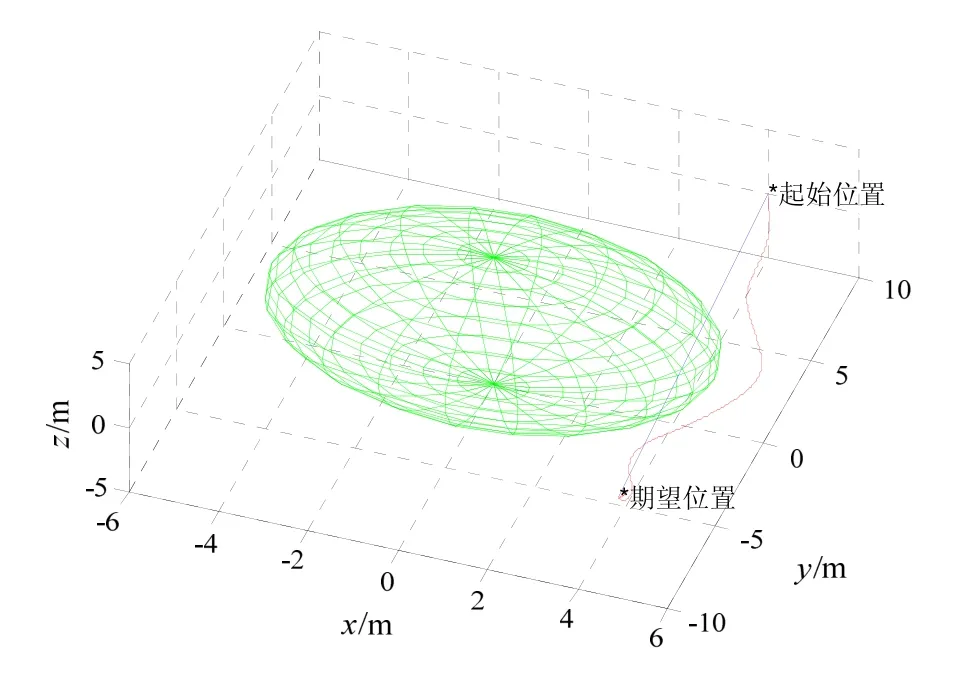
图6 控制器(21)～(24)下追踪航天器运动轨迹Fig.6 Curves of chaser spacecraft’s motion trajectory under controller (21)-(24)

4 结 论

本文基于有限时间控制理论和势函数法对航天器终端接近避碰控制问题进行研究分析，主要结论如下：

1）基于避碰势函数，将终端接近的避碰问题转化为避碰势函数不能等于零的问题，从而为方便其避碰控制器设计提供了模型基础。

2）针对系统外部扰动上界已知的情况，设计了有限时间终端接近避碰控制器，利用双曲正切函数的有界性，使所设计的控制器是有界的。

3）设计了鲁棒自适应有限时间饱和避碰控制器，通过引入辅助系统，使所设计的控制器能够处理扰动上界未知的情况。

4）利用李雅普诺夫理论对所设计的控制器给出了严格的理论证明，表明系统状态为有限时间稳定的，且能实现避碰。

对所设计的控制器进行了数值仿真，进一步验证了所设计控制器的有效性。

（References）：

[1]Deaconu G, Louembet C, Theron A. Designing continuously constrained spacecraft relative trajectories for proximity operations[J]. Journal of Guidance, Control,and Dynamics, 2015, 38(7): 1208-1217.

[2]Guelman M, Aleshin M. Optimal bounded low-thrust rendezvous with fixed terminal-approach direction[J].Journal of Guidance, Control, and Dynamics, 2001, 24(2):378-385.

[3]任家栋, 曾庆双, 朱虹. 地球静止轨道远程交会过程导航性能评估[J]. 中国惯性技术学报, 2016, 24(2): 257-262.Ren J D, Zeng Q S, Zhu H. Performance evaluation of relative navigation algorithm during geostationary orbit long-range rendezvous[J]. Journal of Chinese Inertial Technology, 2016, 24(2): 257-262.

[4]陈统, 徐世杰. 非合作式自主交会对接的终端接近模糊控制[J]. 宇航学报, 2006, 27(3): 416-421.Chen T, Xu S J. A fuzzy controller for terminal approach of autonomous rendezvous and docking with noncooperative target[J]. Journal of Astronautics, 2006, 27(3):416-421.

[5]张大伟, 宋申民, 裴润, 等. 非合作目标自主交会对接的椭圆蔓叶线势函数制导[J]. 宇航学报, 2010, 31(10):2259-2268.Zhang D W, Song S M, Pei R, et al. Ellipse Cissoid-based potential function guidance for autonomous rendezvous and docking with non-cooperative target[J]. Journal of Astronautics, 2010, 31(10): 2259-2268.

[6]Weiss A, Baldwin M, Erwin R S, et al. Model predictive control for spacecraft rendezvous and docking: strategies for handling constraints and case studies[J]. IEEE Transactions on Control Systems Technology, 2015, 23(4):1638-1647.

[7]Qi Y Q, Jia Y M. Constant thrust collision avoidance maneuver under thruster failure[J]. Advances in Space Research, 2012, 49(2): 373-385.

[8]Ma L C, Meng X Y, Liu Z Z, et al. Suboptimal powerlimited rendezvous with fixed docking direction and collision avoidance[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(1): 229-239.

[9]Weiss A, Petersen C, Baldwin M, et al. Safe positively invariant sets for spacecraft obstacle avoidance[J]. Journal of Guidance, Control, and Dynamics, 2014, 38(4): 720-732.

[10]Guo Y, Song S M, Li X H. Quaternion-based finite time control for attitude tracking of spacecraft without unwinding[J]. International Journal of Control, Automation, and Systems, 2015, 13(6): 1351-1359.

[11]Guo Y, Song S M, Li X H. Finite-time output feedback attitude coordination control for formation flying spacecraft without unwinding[J]. Acta Astronautica, 2016, 122:159-174.

[12]Li X H, Song S M, Guo Y. Multivariable super-twisting sliding mode approach for attitude tracking of spacecraft[C]//The 34th China Control Conference. Hangzhou,2015: 5789-5794.

[13]Li S, Wang X. Finite-time consensus and collision avoidance control algorithms for multiple AUVs[J]. Automatica, 2013, 49(11): 3359-3367.

[14]Zhou N, Xia Y. Coordination control of multiple Euler-Lagrange systems for escorting mission[J]. International Journal of Robust and Nonlinear Control, 2015, 25(18):3596-3616.

[15]Chen J, Gan M, Huang J, et al. Formation control of multiple Euler-Lagrange systems via null-space-based behavioral control[J]. Science China Information Sciences, 2016, 59(1): 1-11.

[16]Zhang B Q, Song S M. Decentralized coordinated control for multiple spacecraft formation maneuvers[J]. Acta Astronautica, 2012, 74: 79-97.

[17]Kristiansen R. Dynamic synchronization of spacecraft[D]. Trondheim: Norwegian University of Science and Technology, 2008.

Finite-time and collision avoidance control for spacecraft terminal approach with input saturation

LI Xue-hui1, SONG Shen-min1, CHEN Hai-tao1, GUO Yong2
(1. Center for Control Theory and Guidance Technology, Harbin Institute of Technology, Harbin 150001, China;2. School of Automation, Northwestern Polytechnical University, Xi’an 710072, China)

This paper solves the avoid collision problem of spacecraft terminal approach to realize that a chaser spacecraft does not collide with the target spacecraft when reaching to the expected target point. The spacecraft relative motion and the collision avoidance model are established under the orbital coordinate system of target spacecraft. Two finite-time collision avoidance controllers are presented respectively in cases with/without knowing the upper bound of external disturbances, and the designed controllers have input saturation characteristics. Finally, Lyapunov stability theory is applied to prove the finite-time convergence of the designed controllers, and the collision avoidance potential function is used to prove that the controllers can realize the collision avoidance. Simulations demonstrate the effectiveness of the proposed controllers.

terminal approach; collision avoidance control; finite-time control; input saturation

1005-6734(2017)04-0530-06

10.13695/j.cnki.12-1222/o3.2017.04.019

V448.234

A

2017-04-17；

2017-07-20

国家自然科学基金（61174037，61333003，61021002）

李学辉（1988—），男，博士研究生。E-mail: lxh_hit@126.com

联 系 人：宋申民（1968—），男，教授，博士生导师，研究方向为非线性系统的稳定性分析、鲁棒控制、导弹制导与飞行器控制。E-mail: songshenmin@hit.edu.cn