惯导速度辅助下GNSS高精度定位

陈 刚，王一帆，傅金琳，胡 才，路 寅，李 达

（天津航海仪器研究所，天津 300131）

惯导速度辅助下GNSS高精度定位

陈 刚，王一帆，傅金琳，胡 才，路 寅，李 达

（天津航海仪器研究所，天津 300131）

传统的卫星导航接收机无法同时适应高动态和高精度要求。对于10g以上的加速度，高精度接收机很难达到高精度的指标，甚至基带环路失锁无法正常导航定位。针对GNSS动态条件下高精度定位需求，引入惯性/卫星深组合导航技术，在应用惯性信息辅助接收机减小基带跟踪环路带宽基础上，采用码片窄相关方法降低伪距抖动误差，提高动态条件下GNSS伪距定位精度。仿真结果表明：通过惯性信息辅助跟踪环路可实现较小跟踪环路带宽下的稳定跟踪；在此基础上，通过码片窄相关方法并提高射频前端带宽可实现定位精度的提高。对比传统的伪距定位方法，定位精度(1σ)从6 m提高到3 m左右。

伪距定位精度；窄相关；惯导速度辅助；射频前端

卫星导航接收机实时跟踪卫星的多普勒频移和码相位，对于高动态接收机而言，用户和卫星之间多普勒频移和码相位变化很快，为了保持基带跟踪环路的持续跟踪状态，跟踪环路的带宽不得不增大。由于环路带宽增大，导致跟踪精度以及定位精度的下降。对于传统接收机而言，高动态和高精度是两个互相矛盾的要求。深组合系统中，惯性导航信息可以提供给接收机跟踪环路多普勒频移的估计值，导致载体动态应力对跟踪环路的影响降低。

基于此，可以设计出在高动态下有惯导辅助的跟踪环路，并在此基础上研究高精度定位的方法。

1 惯导辅助下动态接收机设计

当载体进行大机动时，由于跟踪的卫导信息化变化范围较大，要求接收机的跟踪环路具有较宽的带宽，以减小动态应力误差，提高跟踪环路性能，使卫星信号不至于失锁。然而，环路带宽的增大又削弱了接收机环路对于干扰噪声滤除能力，削弱了卫导接收机的抗干扰能力，严重时噪声引起的跟踪误差也会导致卫星信号丢失。为解决环路的动态响应性能与噪声对应环路带宽的矛盾，通常在卫导接收机环路中引入惯导速度信息，降低载体高动态对环路带宽的要求。

如图1所示，假设卫导载波跟踪环采用二阶锁相环回路，当跟踪环的输入信号中掺杂着噪声信号时，环路中的滤波器对噪声信号起滤除作用，不同的滤波器滤除噪声的能力各不相同，可以用环路带宽来反映跟踪环路对输入噪声的滤除能力。

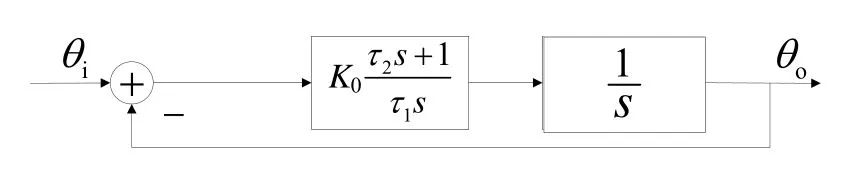
图1 二阶锁相环结构示意图Fig.1 Second-order PLL

载波跟踪环路对应的传递函数为

式中，K0为环路滤波器的增益，1τ和2τ为滤波器的时间常数。在卫导接收机所接收的卫星信号中，掺杂着干扰噪声，为了减小外界干扰噪声对系统测量的影响，要求环路滤波器的带宽越小越好。但滤波器的带宽又直接影响整个跟踪回路的等效环路带宽，若滤波器的带宽很小，则可能无法满足超高动态的要求。为此，将惯导测得的载体速度信息作为一个辅助信号，加到跟踪环路上，即利用惯导速度辅助卫导接收机环路，可以补偿动态应力对跟踪环路的影响。

惯导速度的辅助降低了高动态对环路带宽要求，使系统能很好地跟踪载体的大机动运动。

图 2为惯导速度辅助卫导接收机跟踪环的原理图，a/(s+a)是用来限制惯性传感器带宽的低通滤波器，w(s)为外部相位噪声，e(s)为惯导估计的多普勒频移误差。载体相对于卫星的速度引起多普勒频移，在接收机跟踪环内，惯导速度辅助实际上是将速度转化为多普勒频移，通过这种前馈模型，惯导系统对载波锁相环提供外部频率辅助，使这种组合模式比单纯的锁相环获得更加优异的性能，使等效环路带宽大大增大，对载体的动态跟踪能力更强。

图2 惯导信息辅助的载波跟踪滤波环路示意图Fig.2 INS velocity-aided carrier tracking filter loop

假设e(s)的输入为零，则有：

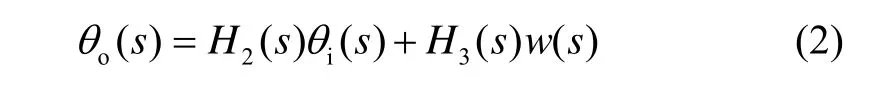
式中，

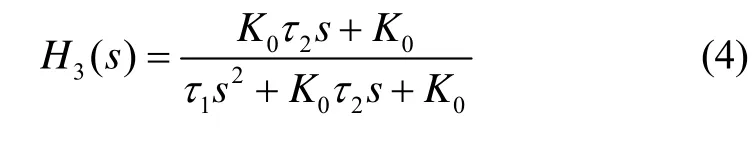
式中，a为惯导带宽限制参数。

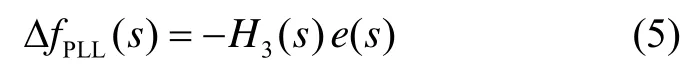
由式(2)和(5)还可以看出，在惯导速度辅助接收机环路设计中，与未辅助环路相比，不需要考虑载体的高动态影响，环路带宽可以做得更窄些，因此对噪声的抑制能力更强。

2 提高惯导辅助下动态接收机伪距定位精度的方法

2.1 提高射频前端带宽可以提高伪距定位精度

射频前端带宽（RF）起到滤除噪声和带外干扰的作用，此带宽也就是以后 GPS接收机工作的信道带宽，它对接收机的性能有很大的决定作用。由于伪码的频谱是sinc函数，所以所接收的中频信号的频谱就是被中频载波调制后的sinc函数。中频信号频谱的大部分能量集中在主瓣上，射频前端带宽越大，相关函数的失真越小，跟踪误差就越小。

工程中由于受到射频前端的限制，码边沿的高频分量被滤波器滤除导致实际的跟踪误差较大。从图3可以看出，射频前端带宽是码速率（fc）的两倍和20倍时码片的恢复情况，明显看出20倍时码片恢复得更好。

图3 不同带宽数字信号的波形差异Fig.3 Difference among digital signal waveforms with different bandwidths

提高射频前端带宽有助于C/A码的恢复，从而提高定位精度，下文会再提到射频前端对码环的影响。

伪距定位精度与射频前端带宽相关。伪距是由C/A码测出来的，而C/A码带宽理论上是无限宽的，这样射频前端带宽就可以决定C/A码的恢复程度，也就直接决定着伪距精度。

由于模拟器射频前端带宽是10 MHz，为了拟合现有导航型接收机的射频前端带宽（2.046 MHz），要把带宽压窄，研究射频前端带宽2 MHz时如何提高定位精度，除此以外，我们也可以通过对射频前端2 MHz和10 MHz对定位精度的影响做对比，验证提高射频前端带宽有助于提高定位精度的理论。

C/A码其功率谱主瓣宽度是 2.046 MHz，因此射频带宽最小为 2.046 MHz，导航型接收机普遍采用最小射频带宽的设计，本文在卫星信号模拟源上用软件方法拟合导航型接收机的射频前端带宽，研究导航型接收机提高精度的方法。对同一段时间模拟源产生的卫星信号进行采样、存储、回放，确保处理的卫星星座信息一致，统计的定位精度能说明与卫星星座无关。

对模拟器进行中频信号采样，采样率为62 MHz，得到频谱图4（映射回模拟域）。我们可以看到大致在4～27 MHz较为平坦。由于进入模拟器射频前端的信号没经过解扩，那么我们认为进入模拟器的信号从频域上看仍旧像白噪声，从GPSL1采样频谱图看出，幅度谱相当于白噪声通过了射频前端的滤波，可以认为23 MHz就是射频前端的通频带。

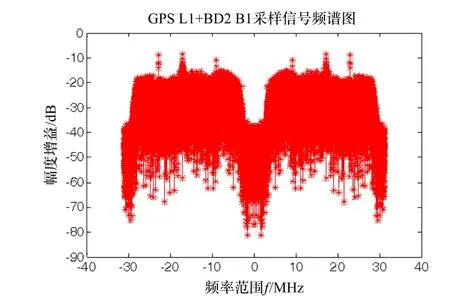
图4 GPS L1+BD2 B1采样信号频谱图Fig.4 GPS L1+BD2 signal frequency domain

图4中，8.58 MHz左右为GPS L1频段信号，考虑到信号还原频域的对称性，对其有用的前端带宽为10 MHz左右。

为了把模拟器射频前端带宽压缩到与导航型接收机的射频前端带宽一致，将模拟器8.58 MHz频点双边1.023 MHz带宽的信号（C/A码主瓣带宽）提取出来，模拟硬件接收机L1频点射频前端带宽。

一般来说，滤波会产生群时延和信号的失真，但是由于采用Matlab后处理软件接收机，可以利用非因果系统使得群时延消除，可以利用FIR线性相位滤波器使得信号不失真。

设计思路是将分段采样的信号周期延拓，采用200阶FIR滤波器进行卷积，选取中间固定位置卷积完全的点做截断，使得FIR滤波器中间点与零时刻对齐。经滤波后信号频谱如图5（映射回模拟域）所示。

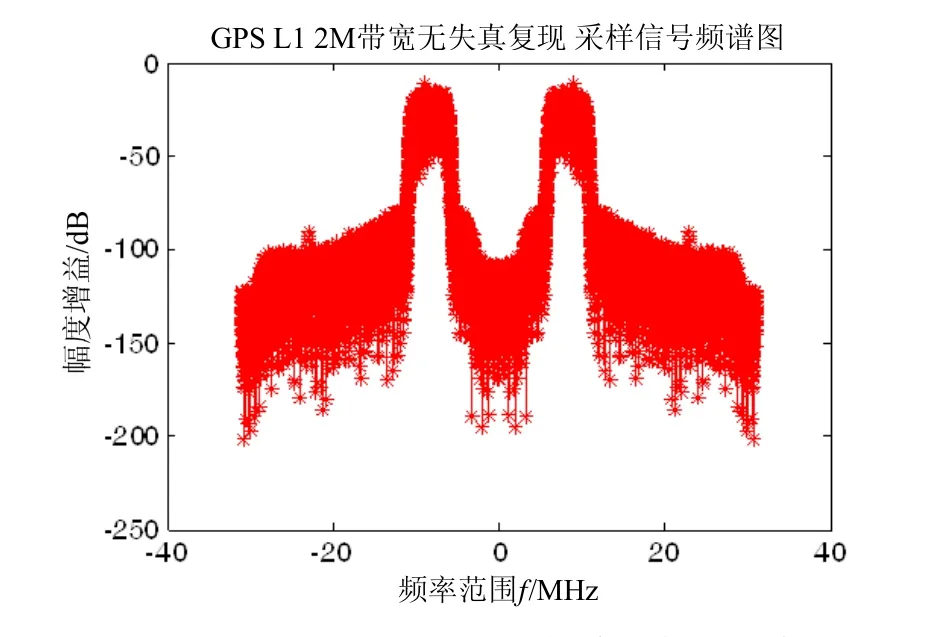
图5 GPS L1频点2MHz带宽采样信号频谱图Fig.5 GPS L1 2MHz bandwidth signal frequency domain

值得注意的是，可以由该方法把模拟器的射频前端带宽减小到10 MHz以下的任意带宽。模拟器自带白噪声。

2.2 减小码环相关间距可以提高伪距定位精度

由于伪距是由码环输出的信息，所以伪距精度与码环跟踪抖动直接相关。

本节通过码跟踪环路鉴相器、噪声特性分析、跟踪抖动的计算，最后得出码环跟踪抖动的估计公式。后文会根据公式提高伪距精度。

2.2.1 码跟踪环路鉴相器相位估计

在系统稳定工作的情况下，接收机载波能够提供相干载波。因此，在分析码跟踪精度时可以忽略载波的作用，采用基带模型。码环鉴相器相位的估计采用归一化超前减滞后幅值法，其数学表示如下：

式中：D为相关间距，即超前码和滞后码之间的间隔码片数；为滞后支路相关值；为超前支路相关值。

设码环输入信号r(t)为输入码和噪声之和，即

超前、滞后支路相关值为：

式中：t为当前时刻；T为相干积分时间；Tc为码元时间宽度。

在无噪声的情况下，该鉴相器能正确锁定相位差异ε，鉴相增益为1。

2.2.2 码跟踪环路鉴相器中噪声特性分析

本节讨论在码延迟鉴相器输入输出端的噪声分量。假设输入噪声信号是均值为0，功率谱密度为N0/2的白噪声。噪声在超前与滞后支路的输出信号分别为：

由于C/N0＞＞10 dB，因此忽略由噪声引起的对分母项的影响，于是有：

于是：

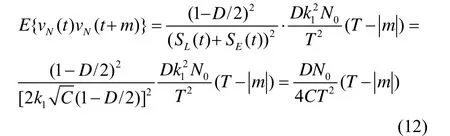
由于设计的鉴相器增益为1，所以：

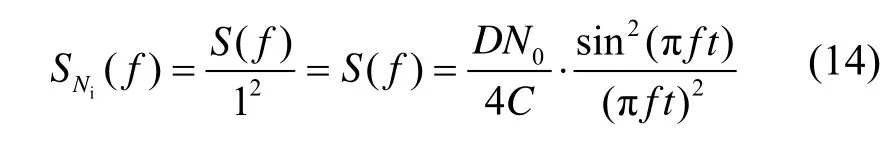
由上述讨论可知， 输入噪声经码环鉴相器处理后变成了非白噪声，在鉴相器模型中，相当于在输入码相对延迟信号τ/Tc上附加了一个非白噪声，Ni(t)的均值为0，功率谱密度为

2.2.3 码跟踪抖动计算

环路输出端噪声方差为：

在环路带宽BL远小于积分带宽1/T时，就可以用输入噪声 0频率处的谱密度来近似计算输出噪声的谱密度，从而得到由加性输入噪声产生的码延迟跟踪抖动为

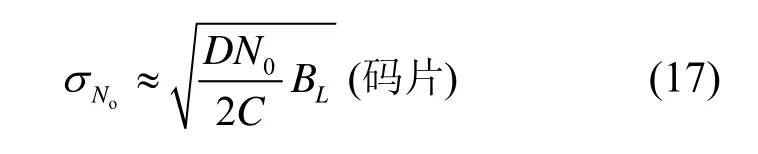
以上我们讨论了在输入是白噪声且码边沿正常的理想情况下的码延迟跟踪抖动，然而事实上工程中由于受到射频前端的限制，码边沿的高频分量被滤波器滤除导致实际的跟踪误差要比这个大。

接收的中频信号的频谱就是被中频载波调制后的sinc函数。中频信号频谱的大部分能量集中在主瓣上，当相关间距D=1码片时，超前和滞后两相关器通常工作在自相关函数主峰左右两边最陡峭的部分，这能让码环具有更高的敏感性。然而，当码环采用窄相关技术时，超前和滞后相关器的相位工作点会在较为平滑的自相关函数主峰顶端附近，使鉴相器工作时误差较大，使得锁相环到达稳定状态收敛较慢，码环的敏感性降低。如果想用相关间距相对较小的窄距相关技术，那么C/A码信号中的更多高频成分必须被保留，在窄相关技术中副瓣对相关函数的影响较大，所以窄相关技术射频前端带宽至少包括第一副瓣。射频前端带宽越大，相关函数的失真越小，跟踪误差就越小。

本节经过计算得到码环跟踪抖动的计算公式，并且得到跟踪抖动实际情况与环路带宽、相关间距、载噪比直接相关，与射频前端带宽间接相关。

3 实验仿真

3.1 惯导辅助下动态接收机跟踪仿真

本实验仿真验证在惯导速度辅助情况下，可以实现较小环路带宽的正常跟踪。

仿真环境为Matlab软件接收机。采用卫星模拟源和中频信号采样回放器录入数据。

卫星有9颗，卫星信号功率统一设置为-123.9 dBm。录入数据后存储，事后处理数据。

仿真中载体的初始速度为北向10 m/s，加速度为北向 10g，此时能够捕获的卫星有 2、5、7、8、10、15、26、29。卫星信号从模拟器采集，根据此时卫星和载体的相对位置，映射到每个星连线上的加速度数值依次约 71 m/s2、23 m/s2、67 m/s2、19 m/s2、15 m/ s2、24 m/s2、0.16 m/s2、7 m/s2，其中，相关间距D=1，射频前端带宽10 MHz，码环环路带宽2 Hz，载波环环路带宽5 Hz。

如图6所示，纵坐标表示I支路累加值，是解调后的数字信号。我们发现不加辅助时跟踪环路失锁，加上速度后可以环路正常跟踪。仿真结果说明，通过惯导速度辅助，卫导跟踪环路能够在较小的带宽下实现对较大动态范围的稳定跟踪。

图6 8号星跟踪结果Fig.6 Tracking results of the satellite 8

3.2 惯导辅助下动态接收机高精度定位仿真

3.2.1 射频前端带宽固定2M时，减小相关间距

前面提到惯导辅助情况下，可以缩小环路带宽，下面研究在5 Hz带宽下如何实现高精度定位。再看式(16)：

这个经计算得到的码环热噪声的估计公式，前提是射频前端带宽无限宽，载波能够完全剥离。

真实情况精度有理由认为精度与表达式中变量有关系。

设定仿真条件如下：固定射频前端带宽为 2.046 MHz，码环带宽为 5 Hz，二阶传统锁相方法；20 Hz载波环带宽，三阶传统锁相方法，无载波辅助，单频点单点定位。

在环路带宽固定，载噪比一定，卫星星座一样的情况下，减小相关间距。

如图7所示，相关间距为1时，跟踪精度（ENU）方差为33.7 m2统计值。

如图8所示，在对相关间距D为1/4时，跟踪精度（ENU）方差为 15.2 m2统计值。可以看出，在其他量不变的情况下误差进一步变小。

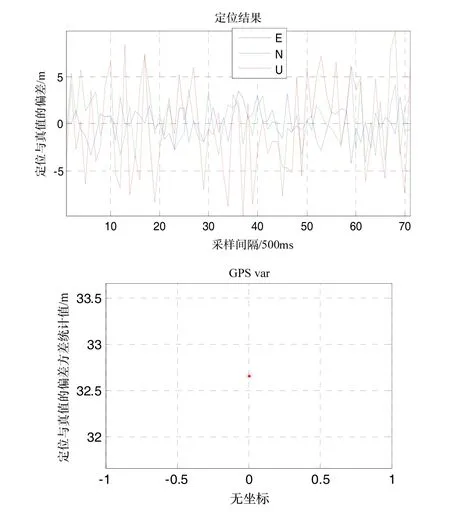
图7 D=1，射频前端带宽2 MHz时定位误差Fig.7 Positioning error when D=1 and RF=2 MHz

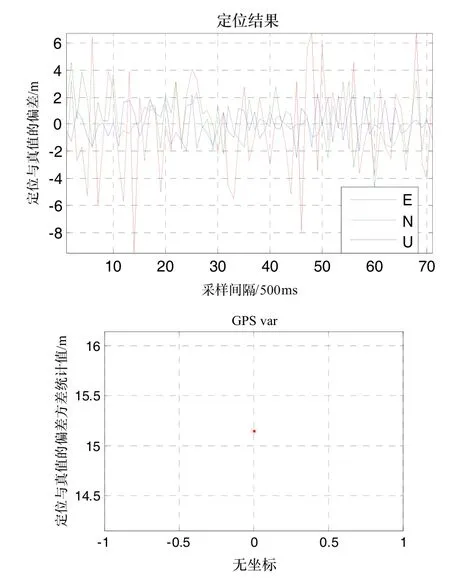
图8 D=1/4，射频前端带宽2 MHz时定位误差Fig.8 Positioning error when D=1/4 and RF=2 MHz

如图9所示，当D=1/32时，定位开始跳大值，定位结果在5000 ms以后收敛。

分析这个问题造成的原因：射频前端带宽是2 MHz，相关结果在峰值处没有尖峰，导致鉴相器不能很好地辨别相位信息，码环跟踪灵敏度变差，使得码环由捕获到跟踪的时间很长，定位结果收敛很慢。当噪声过大时，码环可能会失锁。

我们发现，射频前端带宽2 MHz时，采用减小相关间距的方法当D=1/8时，在不影响环路动态特性的情况下，精度将提到最高。下面我们在D=1/16时提高射频前端带宽。

图9 D=1/32，射频前端带宽2 MHz时定位误差Fig.9 Positioning error when D=1/32 and RF=2 MHz

3.2.2 相关间距D=1/16时，增大射频前端带宽

对于D=1/16的情况，D从1/8到1/16，射频前端带宽2 MHz不能提升精度，此时考虑采用10 MHz射频前端带宽。

如图10～11所示，试验表明10 MHz精度可以进一步提升，且初始定位时不跳大值。由于10 MHz射频前端带宽大，使得相关结果尖峰值比2 MHz情况尖锐，鉴相器的灵敏度更好，使得码环从捕获进稳定跟踪的时间较小。除此以外，由于鉴相器的灵敏度更好，跟踪精度也会得到进一步提升。

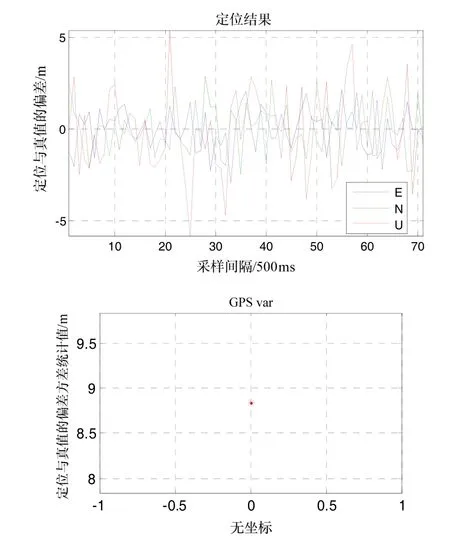
图10 D=1/16，射频前端带宽10 MHz时定位误差Fig.10 Positioning error when D=1/16 and RF=10 MHz

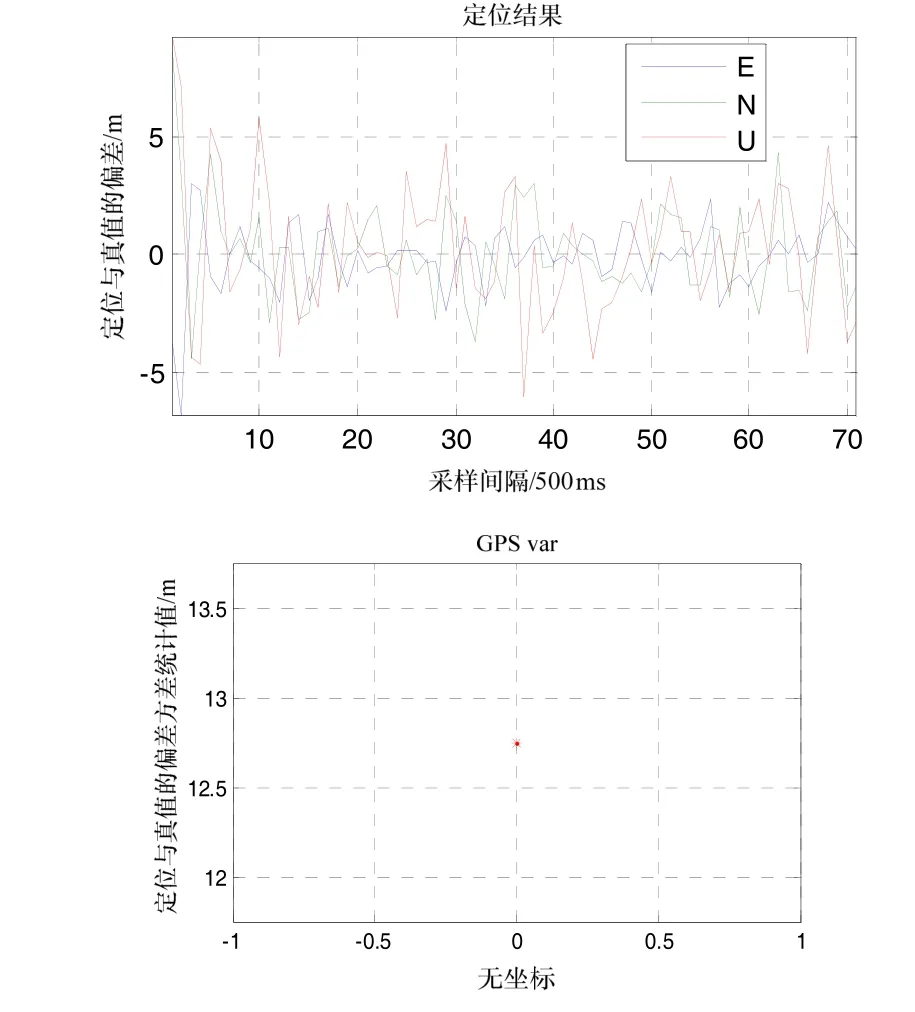
图11 D=1/16，射频前端带宽2 MHz时定位误差Fig.11 Positioning error when D=1/16 and RF=2 MHz

对所做定位实验的统计结果列入表1。

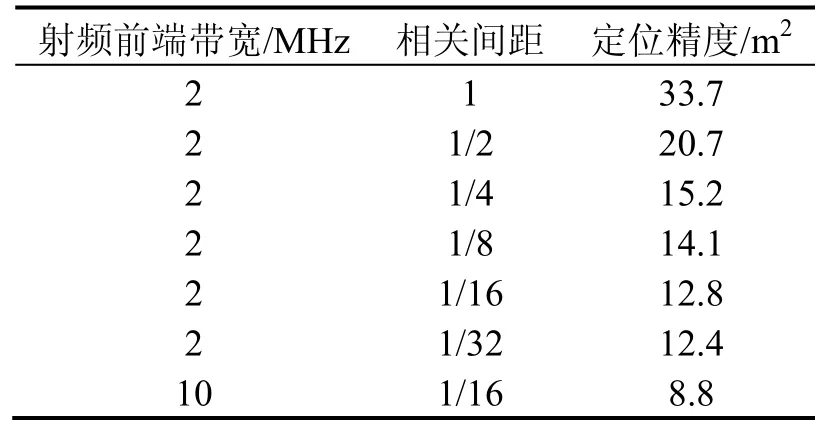
表1 不同条件下定位精度对比Tab.1 Positioning errors in different situations

4 结 论

通过引入惯导辅助的方法，在载体高动态的情况下，对跟踪环路多普勒进行外部补偿，可以把码环带宽压缩。对于码环环路带宽固定的情形，可以通过减小相关间距D来提高伪距定位精度，但是D减小到一定水平，码环鉴相器鉴相灵敏度变差，跟踪精度不会随着D的再减小得到提高。如果想在此基础上再提高精度，需要提高射频前端带宽。

对于 GNSS，定位精度和动态性能一般来说不能同时保证。本文采用惯导辅助的方法，补偿了跟踪环路动态适应性。在环路带宽很窄的情况下，系统仍然可以正常跟踪，动态性能得到极大的提高，这时只需单纯考虑精度的提高，体现了深组合系统的优越性。在此基础上，通过码片窄相关方法，并提高射频前端带宽，可实现定位精度的提高。对比传统的伪距定位方法，定位精度（1σ）从6 m提高到3 m左右。

（References）：

[1]Zhang T S, Zhang H P, Ban Y L, et al. Hardware implementation of a real-time MEMS IMU/GNSS deeply-coupled system[J]. IEICE Transactions on Communications,2013, 96(11): 2933-2942.

[2]Groves P D. Receiver interface requirements for deep INS/GNSS integration and vector tracking[J]. Journal of Navigation, 2010, 63(63): 471-489.

[3]Zhang T, Zhang H, Ban Y, et al. Tracking loop model and hardware prototype verification of GNSS/INS deep integration[J]. Lecture Notes in Electrical Engineering,2014: 553-572.

[4]Martin H, Groves P D, Newman M, et al. A new approach to better low-cost MEMS IMU performance using sensor arrays[C]//Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation. 2013:2125-2142.

[5]Martin H, Groves P D, Newman M, et al. A new approach to better low-cost MEMS IMU performance using sensor arrays[C]//Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation, 2013:2125-2142.

[6]Zhao S H, Lu M Q, Feng Z M. Implementation and performance assessment of a vector tracking method based on a software GPS receiver[J]. Journal of Navigation,2011, 64: 151-161.

[7]Zhao Sihao, Akos D. An open source GPS/GNSS vector tracking loop – Implementation, filter Tuning, and results[C]//ION International Technical Meeting. 2011: 1293-1305.

[8]Zhao S, Powell S, Lu M, et al. Deep Integration of GPSINS based on a software defined receiver – Implementation and test results[C]//International Tech- nical Meeting of the Satellite Division of the Institute of Navigation, ION GNSS. 2014.

[9]Abbott A S, Lillo W E. Global positioning systems and inertial measuring unit ultra-tight coupling method. US:6516021 B1[P]. 2003.

[10]Gustafson D, Dowdle J, Flueckiger K. A deeply integrated adaptive GPS-based navigator with extended range code tracking[C]//IEEE Position Location and Navigation Symposium. 2000: 118-124.

[11]Gustafson D E, Dowdle J R, Elwell J M. Deeplyintegrated adaptive GPS-based navigator with extendedrange code tracking. US: 6331835 B1[P]. 2001.

[12]Mahmoud A R. Tightly coupled integration of GPS precise point positioning and MEMS-based inertial systems[J]. GPS Solution, 2015, 19(4): 601-609.

[13]Youssef T, Phillip T, Cynl B, et al. Implementation and performance of a GPS/INS tightly coupled assisted PLL architecture using MEMS inertial sensors[J]. Sensors,2014, 14(2): 3768-3796.

[14]Bach-Phi D, Vinh-Hao N. Development of a GPS/INS integrated navigation system for model aircraft[C]//International Conference on Control, Automation and Systems. 2014: 201-206.

[15]Li C J, Yang S X. Optimization of the carrier tracking loop for GPS high dynamic receivers[J]. Journal of Beijing Institute of Technology, 2012, 21(2): 164-171.

[16]赵琳, 赵洪斌, 闫超. 复杂环境下INS 辅助GPS跟踪环路研究[J]. 传感器与微系统, 2011, 30(10): 22-25.Zhao Lin, Zhao Hong-bin, Yan Chao. Study on tracking loops of INS-aided GPS in complex environment[J]. Transducer and Micro-system Technologies, 2011, 30(10): 22-25.

High-accuracy positioning of INS velocity-aided GNSS

CHEN Gang, WANG Yi-fan, FU Jin-lin, HU Cai, LU Yin, LI Da
(Tianjin Navigation Instruments Research Institute, Tianjin 300131, China)

Traditional satellite navigation system cannot simultaneously meet high-dynamic and highaccuracy requirements. When the acceleration is ＞10g, the high-accuracy receiver is hard to meet its highaccuracy requirement, and the base-band loop may even lose tracking, leading to abnormal positioning. To solve this problem, a deep-integrated GNSS/SINS navigation system is introduced to meet the high-accuracy positioning demand with high dynamic receiver. Based on decreasing the bandwidth loop bandwidth with INS velocity-aided receiver, the narrow correlation spacing is used to decrease the pseudo-positioning error.Test results show that the inertial information aided tracking loop can realize the stable tracking with narrow bandwidth of tracking loop, and then by using the proposed narrow correlation spacing method and increasing the RF front-end bandwidth, the positioning accuracy can be improved. Compared with traditional pseudo-positioning method, the positioning error (1σ) by the proposed method is decreased to about 3 m from 6 m.

pseudo-positioning precision; narrow correlator spacing; INS velocity-aided GNSS; RF front end

1005-6734(2017)04-0466-07

10.13695/j.cnki.12-1222/o3.2017.04.008

U666.1

A

2017-04-12；

2017-06-12

海军武器装备预研项目（302010701）

陈刚 （1973—），男，研究员，硕士生导师，研究方向为导航、制导与控制。E-mail: 540366804@qq.com