基于MSCMG大型遥感卫星高精度姿态控制方法

舒 适，房建成，张 伟，刘 刚，钱 勇，方宝东，刘 虎

基于MSCMG大型遥感卫星高精度姿态控制方法

舒 适1,2,3，房建成1,2,3，张 伟4，刘 刚1,2,3，钱 勇4，方宝东4，刘 虎1,2,3

（1. 北京航空航天大学 仪器科学与光电工程学院，北京 100191；2. 新型惯性仪表与导航系统技术国防重点学科实验室，北京 100191；3. 惯性技术重点实验室，北京 100191；4. 上海卫星工程研究所，上海 201109）

针对大力矩飞轮前馈和闭环反馈补偿复杂、对精度影响敏感性大的问题，提出了基于磁浮控制力矩陀螺闭环补偿的大型遥感卫星高精度姿态控制方法。该方法采用磁悬浮力矩陀螺为控制执行机构，通过变结构反馈补偿控制律设计，建立新的运动补偿控制系统，减小相机和卫星本体耦合效应。基于磁浮力矩陀螺力矩大、反向激励扰动小、精度高的特性，将其应用于对地遥感成像相机运动补偿控制系统中，仿真结果表明，与飞轮前馈补偿相比，姿态稳定度提高了一个数量级，有效提高空间大惯量卫星姿态控制的稳定度，提升相机对地成像质量；研究结果可为甚高精度卫星姿态控制与载荷运动补偿提供参考。

遥感卫星；磁浮控制力矩陀螺；相机运动；反馈补偿；高精度姿态控制

大型遥感卫星主要利用可见光、红外、微波等主载荷，通过摄影、扫描、信息感应探测等形式，识别获取探测目标特性和运动状态数据，实现对变化目标的持续监视、快速成像和巡查成像。遥感卫星的分辨率与卫星姿态控制精度和稳定度密切相关。有效载荷工作时（如红外扫描相机、凝视跟踪相机等），其运动导致的干扰力矩将直接对遥感卫星姿态控制精度与成像分辨率产生影响。卫星在稳定运行状态下的主要姿控执行机构是动量轮。若红外扫描相机和凝视相机联合工作时产生的干扰力矩大于动量轮组的输出力矩，将使得干扰力矩短时间内无法被动量轮吸收，降低了卫星姿态稳定度，从而影响载荷成像质量。

为在不降低转动部件角加速度和角速度的前提下，减小有效载荷扫描运动对成像质量的影响，国内外学者提出了基于前馈控制器补偿扫描运动的方法。K.Yamada等采用地面机械臂运动方程表示未知线性函数，并将其应用到具有活动部件的卫星姿态控制系统设计中，但该方法在控制过程中需要实时估计位置参数，大大增加了星载计算机的负担[1-4]。利用动量定理对扫描运动产生的角动量进行估计采用了一种将红外扫描相机的角动量作为前馈信号，前馈控制器的输出作为内反馈的“反馈-前馈”复合控制方法。“反馈-前馈”复合控制方法能有效减小相机扫描镜运动对卫星姿态稳定度的影响，但这种方法大大增加了控制系统的复杂性[5-11]。为获取更高空间分辨率的对地观测数据，需要采用新的控制方法以进一步减小相机和卫星本体耦合效应，提高姿态控制精度。

本文以大型遥感卫星为背景，在分析大力矩飞轮前馈补偿和闭环反馈补偿方法特点的基础上，提出了一种基于磁悬浮控制力矩陀螺补偿的姿态控制方法。与传统机械支撑控制力矩陀螺相比，磁浮控制力矩陀螺具有转子和定子之间无接触、无摩擦、无需润滑、极微振动和精度高的特点。本文充分利用磁悬浮力矩陀螺的上述优势[12-14]，取消了复杂的控制系统前馈补偿过程以简化控制。通过数值仿真，验证了该方法可用于实现大型遥感卫星的高精度姿态闭环控制。

1 带相机运动的卫星动力学模型

遥感卫星配置扫描相机和凝视跟踪相机条件下，扫描相机以南北扫描模式对观测区域进行扫描观测，扫描相机发现目标后交付凝视相机进行目标捕获和持续跟踪，实现对目标的探测和跟踪。扫描相机南北扫描采用一维运动模式进行推扫，而凝视相机采用扫描和步进两维运动模式实现目标跟踪。

以扫描相机为例进行分析。扫描相机沿滚动轴进行南北扫描，如图1所示。图中以轨道坐标系作为姿态参考坐标系，原点O为卫星质心，Xo轴指向卫星飞行方向，Zo轴由卫星质心指向地心，Yo轴与Xo和Zo构成右手坐标系。类似地，定义卫星本体坐标系在卫星姿态角为零的情况下，本体坐标系和轨道坐标系重合。定义为相机扫描镜坐标系，其三轴坐标系的定义和轨道坐标系类似，图1中β为扫描镜南北方向运动时的扫描角度，p为相机扫描镜光轴对地指向。

图1 相机坐标系示意图Fig.1 Coordinate system of infrared cameras

假设扫描相机扫描幅度最大值β为 20°，扫描周期T为10s，扫描相机运动规律以及各段对应时间如图2所示。设扫描角β自南向北为正向，可以求得扫描角速度和角加速度，并由此得到扫描相机产生的干扰力矩。对凝视相机工作模式可以进行类似的分析，得到其产生的干扰力矩。经分析，凝视和扫描相机合成干扰力矩主要作用在X轴上，因此两台相机运动主要影响卫星的滚动轴。

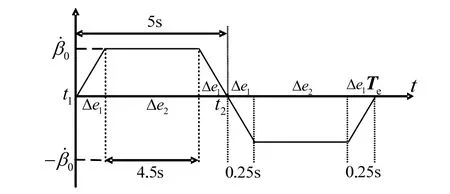
图2 红外扫描相机运动规律Fig.2 Scanning curve of infrared scanning camera

以扫描相机为例，扫描相机和卫星的耦合动力学模型为：

式中：ωB为卫星本体相对惯性空间的姿态角速度；I为卫星惯量矩阵；Td为卫星受到的外干扰力矩；Hs为相机的角动量向量；Is为相机的转动惯量；为扫描相机的匀速扫描角速度；h为控制系统执行机构角动量，为控制系统执行机构控制力矩。

从式(1)可以看出，相机的扫描运动主要影响滚动轴，但由于扫描相机运动与星体存在着轨道角速度的耦合，扫描相机运动的角动量和动量矩在卫星本体三轴上均有分量，因此扫描相机运动时产生的干扰也同时影响俯仰轴和偏航轴，最终影响扫描相机的光轴指向，引起卫星星下点扫描误差，造成扫描图像质量下降。

2 相机运动规律建模和分析

以扫描相机为例进行运动规律建模。根据图2可以得到扫描角角加速度随扫描时间t的变化曲线，如图3所示。

图3 扫描镜加速度随时间变化曲线Fig.3 Acceleration curve of infrared scanning camera

将式(2)分段函数展开为傅里叶级数，可得：

采用同样的方法对以凝视相机进行分析。扫描相机在发现目标之后，凝视相机利用两维扫描机构转动过去，对目标进行快速、连续跟踪。两维扫描机构转动过程中，在滚动和俯仰方向产生加速、匀速和减速运动。由于凝视相机也存在转动惯量，所以在两个方向上产生干扰力矩，影响卫星姿态精度，进而影响凝视相机与目标的光轴指向精度，成像曝光出现偏差像移，最终相机影响成像质量。

利用同样的方法可以得到凝视相机在运动时产生的角加速度、扫描角速度和扫描角以及步进角、步进角速度和步进角加速度。根据相机的运动和角速度和角加速度，可以得到扫描相机和凝视相机运动时产生的干扰力矩，计算和仿真结果如图4所示。

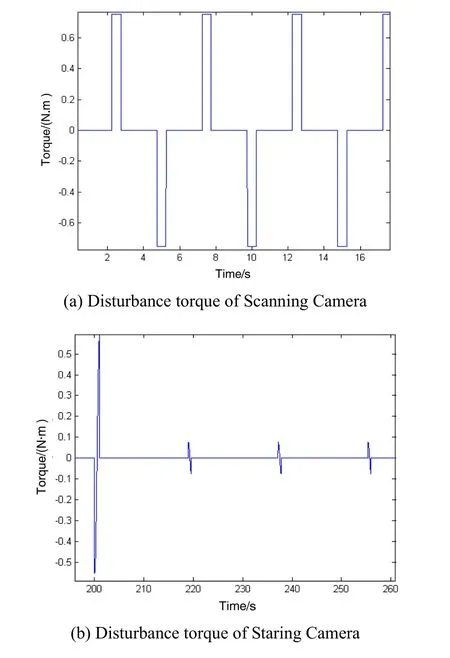
图4 相机运动产生的干扰力矩Fig.4 Disturbance Torques of the cameras motion

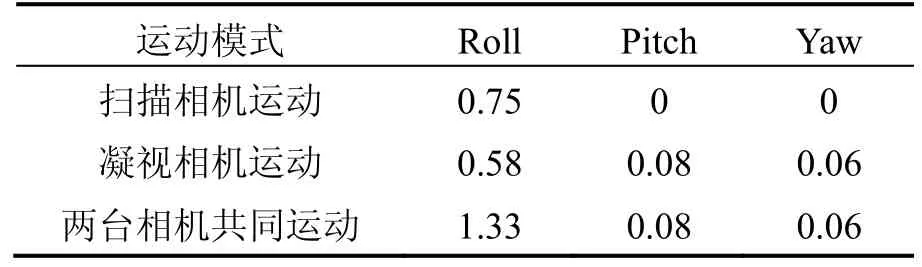
表1 不同运动模式相机运动产生最大干扰力矩（N·m）Tab.1 Maximum torques of the cameras (N·m)

一般地，对控制力矩的补偿方案选用前馈补偿方案，如图5所示，即在相机运动时，利用独立于控制系统执行机构的单独补偿飞轮产生一个与相机运动产生的干扰力矩大小相等、方向相反的控制力矩，补偿相机运动的干扰力矩。

图5 前馈补偿相机运动原理图Fig.5 Schematic of feed forward compensation system

实际上，由于补偿飞轮的输出补偿力矩在大小、方向上和相机运动产生干扰力矩的差异，以及补偿力矩相对于干扰力矩的时延，补偿后必会存在一定的残余干扰力矩，其作用在卫星本体上，姿态与轨道控制分系统通过卫星本体飞轮控制的大回路对其进行缓慢吸收，保证卫星姿态角和角速度满足整星的指标要求。

这种补偿方案需要单独的补偿机构，控制上采用前馈补偿控制，该方法增加了控制系统设计的复杂性。另外，由于前馈补偿是开环控制，对补偿机构的参数稳定性要求较高，否则将会造成新的控制误差。

补偿系统采用前馈方案的主要原因是干扰力矩的频率相对较高，星上姿控系统输出力矩的频率相对较低，无法满足姿态控制系统对干扰抑制的要求；其次，两台相机干扰力矩的幅值、频率、相位等特征是稳定的，且可以以较高的精度进行估算。

当控制系统执行机构的输出力矩大于干扰力矩，并且执行机构单机的响应带宽和控制系统计算机的处理能力满足要求时，可不采用前馈补偿，直接采用控制系统闭环补偿方法，因为干扰产生的姿态误差信息直接进入系统控制回路，误差可以得到不断地修正，控制精度很高。

大力矩执行机构有机械式CMG和MSCMG。机械式CMG在卫星和空间站已应用。机械式CMG存在着轴承高速旋转不平衡振动和润滑等，所产生的干扰力矩直接降低卫星指向精度和姿态稳定度，其转子转向频繁切换，转速频繁过零，静摩擦力矩严重影响其输出力矩精度，影响卫星的控制精度。MSCMG转子和定子之间无接触、无摩擦、无需润滑，具有输出力矩大、极微振动和精度高的特点，非常适用于高敏捷机动和高精度姿态控制要求的大型遥感卫星[15-17]。

利用磁浮控制力矩陀螺大力矩能够抵消作用于卫星外部的大干扰力矩，并提高控制系统的精度，其原理如图6所示。

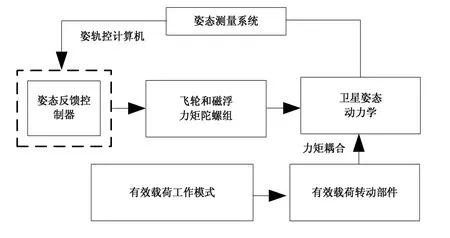
图6 磁浮力矩陀螺反馈控制原理图Fig.6 Schematic of the feedback compensation system

3 磁浮控制力矩陀螺补偿方案设计

3.1 磁浮力矩陀螺补偿方案

磁浮力矩陀螺补偿方案和星上的控制系统密切相关。补偿方案的设计是在控制系统的基础上，对控制系统进行适应性修改。星上姿态控制系统设计为反作用飞轮的安装，采用三个正交加一个斜装方式，每个飞轮的最大输出力矩为0.1 N·m, 控制系统中飞轮的安装方案如图7所示，图中，在卫星本体坐标系下，α为最佳安装角，为54°44′，此时飞轮功耗总和为最小，飞轮角动量平方和也为最小。

图7 大力矩飞轮前馈方案补偿方案Fig.7 Compensation scheme of great-torque flywheel

传统的前馈力矩补偿方案是在滚动轴采用两个大力矩飞轮1和2，两台大力矩飞轮在X轴方向产生一个与相机运动产生的干扰力矩大小相等、方向相反的控制力矩，开环补偿两台相机的运动干扰对卫星的姿态的影响。补偿方案如图7所示。

磁浮力矩陀螺运动补偿方案在前馈力矩方案的基础上进行优化设计，将一台磁悬浮控制力矩陀螺代替两台大力矩飞轮进行控制系统的闭环补偿，控制系统的补偿方案如图8所示。

磁浮力矩陀螺成对安装，控制力矩陀螺角动量方向保持相互平行，且框架轴方向与Z轴平行，力矩陀螺控制力矩补偿滚动轴方向的干扰力矩[18-21]。

图8 磁浮控制力矩陀螺补偿方案Fig.8 Compensation scheme of MGCMG

3.2 磁浮力矩陀螺参数的选取

在不考虑环境力矩、挠性振动、通道间耦合等干扰因素的理想情况下，为了保持本体姿态不变，应当在任意时刻下，保证力矩陀螺动量矩变化完全吸收由于扫描相机运动引起的系统动量矩变化，即力矩陀螺系统输出力矩等于相机运动产生的干扰力矩的负值：

根据式(5a)(5b)和式(1b)可以确定干扰补偿要求的力矩和角动量。根据分析结果，并考虑一定的裕度，选择采用两台角动量15N·ms，输出力矩3N·m的单框架磁浮控制力矩陀螺。

3.3 磁浮力矩陀螺控制规律设计

3.3.1 磁浮力矩陀螺操纵控制律

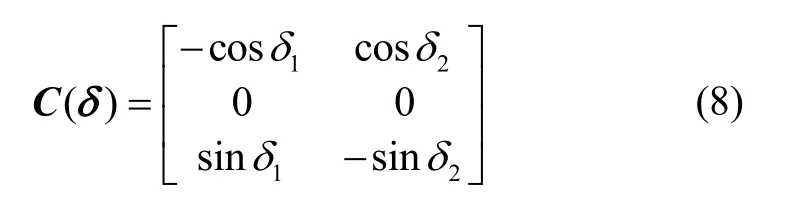
控制力矩陀螺的操纵律存在着奇异问题，当力矩陀螺接近奇异时，指令力矩全部分量分配给反作用飞轮系统，以避免陀螺力矩系统接近奇异时，导致框架角速度过大或无解的现象发生[22]。

3.3.2 控制规律设计

为了减小相机运动时对星体本体耦合效应，磁浮力矩陀螺和飞轮控制律均采用变结构控制。相机运动引起卫星姿态变化的实质是相机运动与星体的耦合使系统参数不断变化，导致系统模型具有不确定性。采用飞轮前馈方法时，由于控制算法鲁棒性不强，卫星对系统参数变化敏感，这将引起卫星姿态的变化。采用变结构控制可克服卫星系统模型的不确定性，提高系统的鲁棒性，为此对控制力矩陀螺和飞轮控制力矩采用变结构控制设计[23-24]。

采用四元数描述的卫星姿态运动学方程为

ωBO为星体相对轨道坐标系的角速度矢量；且ωBO=为星体坐标系与轨道坐标系之间的四元数坐标转换矩阵，0ω为卫星轨道运动角速度。式(10)可写为：

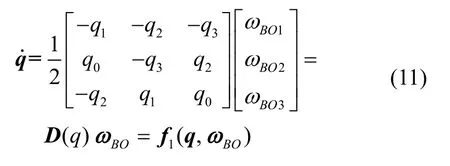
微分式(11)，可得：

基于四元数设计控制规律时，一般将四个非独立的四元数变量截断成三个独立变量进行设计。设方程为

对于对地定向三轴稳定卫星而言，可取

W 为4×4对角正定阵。当S≠0时，选择控制力矩T，使得SS˙<0，从而保证t→∞时，S→0。若存在时刻t0，使得则式(14)满足S=0，也保证了选滑模面满足滑动模态的存在性和可达性。则

所以设计控制力矩Tc为

式(16)中sgn(S)为符号函数矢量，将式(16)代入式(15)中，可得：

由于W 为对角正定阵，因此式(18)构成了以q˙为变量的解耦控制系统。这样控制律中的参数阵W、 K就可以完全根据四元数各个变量的动态变化规律进行设计，从而方便了控制律设计。

3.3.3 控制系统的稳定性分析

对式(11)进行微分，可得：

将式(16)代入式(21)，并将所得结果代入式(20)得：

系统渐进稳定得证。

由于在控制规律中存在符号函数sgn(S)，控制律切换总伴随有滞后，滑动模态不可避免地产生颤振，减小颤振的方法主要是使切换方式“柔化”，采用光滑函数来代替控制律(16)中的符号函数sgn(S)[16,19]。同时利用MSCMG万向偏转输出的高精度、高带宽力矩对卫星平台主动振动控制，也是值得深入的研究方向[12-13]。

4 载荷不同运动模式下数值仿真与分析

取地球半径Re=6371 km，地球引力常数μ=3.986×遥感卫星的轨道半径R0=42164 km，轨道角速度7.292×10-5rad/s，轨道周期为地球自转周期。设定卫星的主转动惯量为扫描相机南北扫描范围为±20°，扫描周期为10s；凝视相机能够东西和南北两维运动实现对目标跟踪，凝视相机跟踪范围为东西±5°，南北±10°；扫描相机沿滚动轴的转动惯量2.3kg·m2，凝视相机在滚动轴的转动惯量为2kg·m2。仿真中均考虑星敏感器和光纤陀螺组成的姿态确定系统，星敏感器测量精度3″，光纤陀螺随机漂移0.02 (°)/s。分析计算中，控制系统执行机构采用输出角动量15N·m·s、输出力矩0.1N·m的反作用飞轮；补偿机构磁浮力矩陀螺角动量15N·m·s，输出力矩3N·m；选用输出角动量15N·m·s，输出力矩1N·m的大力矩飞轮。

在采用飞轮与大力矩飞轮补偿中，主要考虑因素是控制精度、动态响应特性、响应带宽、干扰力矩以及输出力矩同步性和补偿力矩的线性度。在飞轮和大力矩前馈补偿模式中，分别考虑了补偿力矩指令形式与载荷实际干扰力矩的一致性、补偿力矩的补偿精度和补偿力矩的线性度等因素。

采用 MSCMG控制系统闭环补偿中，重点考虑控制精度、动态响应特性、响应带宽、干扰力矩等因素，忽略单机力矩噪声、环境干扰模型因素。将执行机构内部重复控制模型简化为复合控制模型，而不影响仿真结果。

在上述条件下，分别进行四种模式下补偿系统的仿真和分析[25-28]。

仿真模式一：补偿前相机运动对卫星姿态影响

扫描相机南北扫描，凝视相机跟踪模式，进行补偿前控制系统的仿真，两台相机共同作用下滚动轴仿真结果如图9～10所示。

从图 9～10中可以看出，两台相机运动主要影响卫星滚动轴姿态稳定度，由于轨道角速度的耦合，俯仰和偏航轴也受到影响，但是姿态角和姿态角速度均满足指标要求。两台相机运动干扰造成滚动姿态角速度为 1.2×10-3(°)/s，系统的稳定度满足不了控制系统的指标要求。

图9 补偿前相机运动对姿态角影响Fig.9 Attitude angle before compensation

图10 补偿前相机运动对姿态角速度影响Fig.10 Attitude velocity before compensation

仿真模式二：凝视相机运动

单独考虑凝视相机跟踪模式，只考虑对凝视相机沿滚动轴的最大干扰力矩进行补偿。采用磁浮力矩陀螺进行补偿的仿真结果如图11～13所示。

图11 滚动轴姿态角时间历程Fig.11 Time history of roll angle

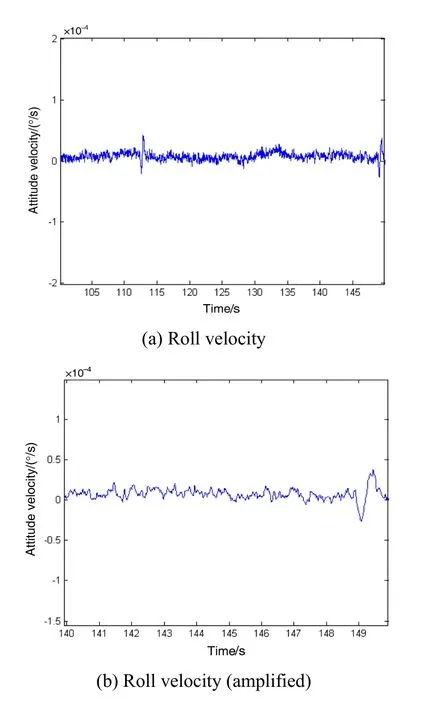
图12 滚动轴姿态角速度时间历程Fig.12 Time history of roll velocity

图13 磁浮力矩陀螺输出力矩时间历程Fig.13 Time history of torque of MSCMG

从图11～13中可以看出，由于凝视相机的在滚动轴产生的干扰力矩相对较小，磁浮力矩陀螺补偿掉了凝视相机在滚动轴上的干扰力矩，滚动轴稳定度达到3.4×10-5(°)/s，滚动轴的稳定度得到极大提高。

仿真模式三：扫描相机运动

只考虑扫描相机进行运动补偿，扫描相机执行南北扫描，采用磁浮力矩陀螺补偿后的仿真结果如图14～16所示。

图14 滚动轴姿态角时间历程Fig.14 Time history of roll angle

图15 滚动轴姿态角速度时间历程Fig.15 Time history of roll velocity

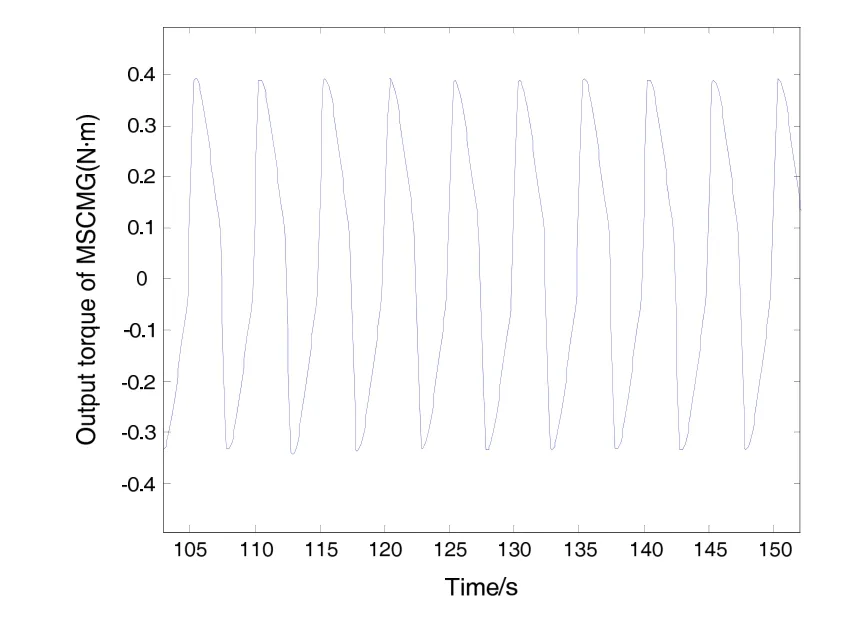
图16 磁浮力矩陀螺输出力矩时间历程Fig.16 Time history of torque of MSCMG

从图14～16中可以看出，扫描相机由于一直进行南北运动，对星体产生的干扰力矩主要影响滚动轴，经过补偿之后，滚动轴姿态稳定度达到4.3×10-5(°)/s，满足控制系统要求。

仿真模式四：两台相机同时运动

扫描相机运动，凝视相机跟踪模式，进行基于磁浮力矩陀螺补偿相机运动的控制闭环系统仿真，仿真结果如图17～19所示。

从图17～19中可以看出，两台相机同时运动对滚动轴姿态影响最大，经过补偿，滚动轴姿态角速度最大值为5.4×10-5(°)/s，满足控制系统要求。

图17 滚动轴姿态角时间历程Fig.17 Time history of the roll angle

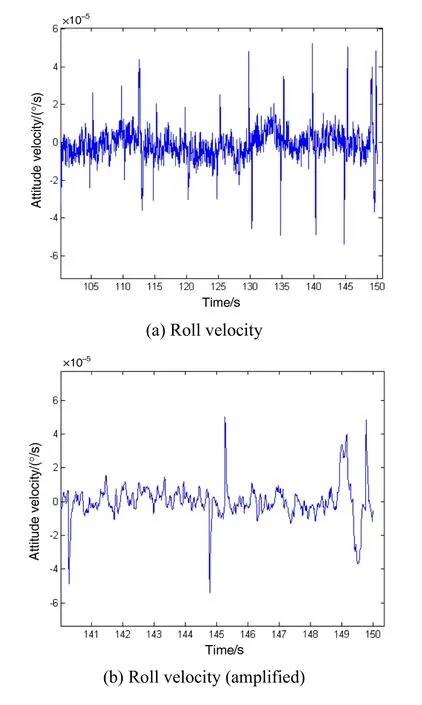
图18 滚动轴姿态角速度时间历程Fig.18 Time history of roll velocity

图19 磁浮力矩陀螺输出力矩时间历程Fig.19 Time history of MSCMG torque

仿真模式五：前馈和反馈控制精度对比

分别采用大力矩飞轮前馈补偿和磁浮控制力矩陀螺反馈补偿进行控制精度对比，两种方案控制系统采用相同的控制规律，仿真结果如图20所示。

以上不同模式下控制达到的精度如表2所示。

从表2中可以看出：两台相机运动主要影响卫星滚动轴的姿态稳定度，偏航和俯仰轴受轨道角速度的耦合，也有一定的影响，但是控制系统飞轮可以将其吸收，不需要进行补偿；其次，采用磁浮力矩补偿三种载荷运动模式，补偿后各项指标均满足要求。

图20 滚动轴姿态角时间历程Fig.20 Time history of roll attitude

表2 相机不同工作模式下补偿效果对比分析Tab.2 Compensation effects for various camera motion patterns

对前馈补偿方案分析得出：力矩补偿飞轮输出力矩同步性相差 0.045 s时产生的最大滚动姿态误差约2.5×10-4(°)/s，其输出力矩线性度在为90%的情况下产生的滚动姿态误差约为2.3×10-4(°)/s。

从表2可以分析得出：当采用MSCMG补偿后，卫星姿态稳定度得到显著的改善，滚动轴姿态角速度最大值为 5.4×10-5(°)/s，稳定度得到了较大的提高，有利于星上相机的遥感成像。

5 结 论

对地遥感卫星载荷工作时产生的扰动力矩必将对卫星姿态控制精度产生影响，从而降低成像分辨率。以前馈补偿控制需要单独的补偿机构，增加了控制系统设计的复杂性。此外，由于前馈补偿是开环控制，易影响参数稳定性，且易引入新的控制误差，因而会影响成像精度。针对这些问题，提出了一种基于磁悬浮力矩陀螺的大型遥感卫星高精度姿态补偿与控制方法。

研究结果形成以下结论：1）本方法提出利用磁浮力矩陀螺力矩大、反向激励扰动小、精度高的特性，以变结构反馈控制来补偿运动干扰力矩，提高了空间大惯量卫星姿态控制的稳定度。建模和仿真结果表明：相对于飞轮前馈补偿，闭环姿态控制平台稳定度得到了较大的提高，有效提升了相机对地成像质量。2）提出了以磁悬浮力矩陀螺作为反馈补偿控制以改进传统前馈补偿的方法，优化了控制系统精度与稳定度。3）本文研究结果为提升空间遥感大载荷在不同工作模式运动条件下的成像分辨率提供了一种新的磁浮控制技术途径，可为大型遥感卫星甚高精度姿态控制与载荷运动补偿设计提供参考。

（References）：

[1]Pong C M, Miller D W. Reduced-attitude boresight guidance and control on spacecraft for pointing, tracking,and searching[J]. AIAA Journal of Guidance, Control,and Dynamics, 2015, 38(6): 1027-1035.

[2]Zhang Cong, Wu Yun-jie, Zuo Jing-xing. Early warning satellite attitude SMC base on ESO[C]//Proceedings of 2014 IEEE Chinese Guidance, Navigation and Control Conference. 2014: 1589-1594.

[3]Zorn A, West M. Optimal attitude scheduling of an imaging satellite[C]//AIAA Guidance, Navigation, and Control (GNC) Conference. Boston, 2013: AIAA-2013-5254.

[4]金涛, 李贞, 李婷, 等. 提高光学遥感卫星图像几何精度总体设计分析[J]. 宇航学报, 2013, 34(8): 1159-1165.Jin Tao, Li Zhen, Li Ting, et al. System design and analysis for improving geometric accuracy of high-resolution optical remote sensing satellite image[J]. Journal of Astronautics, 2013, 34(8): 1159-1165.

[5]Wang Hao, Yang Zhao-hua, Chen Yang, et al. A study on the influence of the satellite attitude accuracy on TDICCD imaging[C]//2012 8th IEEE International Symposium on Instrumentation and Control Technology. 2012: 219-223.

[6]张树青, 张媛, 周程灏, 等. 星载 TDICDD 相机方位扫描像移模型研究[J]. 红外与激光工程, 2014, 43(6):1823-1829.Zhang Shu-qing, Zhang Yuan, Zhou Cheng-hao, et al.Image motion model of azimuthally photography for satellite borne TDICCD camera[J]. Infrared and Laser Engineering, 2014, 43(6): 1823-1829.

[7]李晓云, 杜伟. 星载 TDICDD 相机像移对成像质量的影响分析[J]. 航天器工程, 2011, 20(3): 51-55.Li Xiao-yun, Du Wei. Analysis of image motion effect on satellite TDICDD camera image quality[J]. Spacecraft Engineering, 2011, 20(3): 51-55.

[8]Nguyen N T, Lam Q M. Pointing control accuracy and robustness enhancement of an optical payload system using a direct adaptive control combined with an optimal control modification[C]//AIAA Infotech@Aerospace Conference. 2013, Boston: AIAA-2013-5041.

[9]关新, 郑钢铁. 空间相机隔振与姿态控制一体化设计[J]. 宇航学报, 2013, 34(2): 214-221.Guan Xin, Zheng Gang-tie. Integrated design of space telescope vibration isolation and attitude control[J]. Journal of Astronautics, 2013, 34(2): 214-221.

[10]孙晓峰, 裴胜伟, 李新刚. INR系统用于静止轨道高姿态精度卫星的分析[J]. 航天器工程, 2013, 22(1): 93-100.Sun Xiao-feng, Pei Sheng-wei, Li Xin-gang. Application analysis of INR on GEO satellites with high attitude accuracy[J]. Spacecraft Engineering, 2013, 22(1): 93-100.

[11]Chee S A, Damaren C J. Optimal gyricity distribution for space structure vibration control[J]. Journal of Guidance Control and Dynamics, 2015, 38(7): 1218-1228.

[12]刘虎, 房建成, 刘刚. 基于磁悬浮动量轮微框架能力的卫星滚动偏航姿态稳定控制研究[J]. 宇航学报, 2010,31(4): 1063-1069.Liu Hu, Fang Jian-cheng, Liu Gang. Satellite roll-yaw axis attitude stable control based on magnetically suspended momentum wheel with vernier gimballing capacity[J]. Journal of Astronautics, 2010, 31(4): 1063-1069.

[13]王华, 王平, 任元, 等. 基于磁悬浮控制力矩陀螺的航天器姿态高精度高带宽测量方法[J]. 宇航学报, 2016,37(4): 451-460.Wang Hua, Wang Ping, Ren Yuan, et al. High accuracy and high bandwidth measurement method of spacecraft attitude based on MSCMG[J]. Journal of Astronautics,2016, 37(4): 451-460.

[14]Sasaki T, Shimomura T. Generalized dynamics of a spacecraft with plural MEDs and attitude control with DGVSCMGs via LPV control theory[C]//AIAA Guidance, Navigation, and Control Conference. Kissimmee,Florida, 2015. AIAA 2015-1090.

[15]Ren Yuan, Fang Jian-cheng. High-precision and strongrobustness control for an MSCMG based on modal separation and rotation motion decoupling strategy[J].IEEE Transactions on Industrial Electronics, 2014, 61(3):1539-1551.

[16]邓瑞清, 赵岩, 房建成, 等. 磁悬浮飞轮与机械飞轮干扰特性的对比分析[J]. 宇航学报, 2016, 37(8): 917-923.Deng Rui-qing, Zhao Yan, Fang Jian-cheng, et al. Disturbance characteristics analysis of magnetically suspended and mechanical flywheels[J]. Journal of Astronautics,2016, 37(8): 917-923.

[17]Xu Xiang-bo, Fang Jian-cheng, Wei Tong. Stability analysis and imbalance compensation for active magnetic bearing with gyroscopic effects[C]//2012 8th IEEE International Symposium on Instrumentation and Control Technology. 2012: 295-300.

[18]Fang Jian-cheng, Li Wen-zhuo, Li Hai-tao. Self-compensation of the commutation angle based on DC-Link current for high-speed brushless DC motor with low inductance[J]. IEEE Transactions on Power Electronics.2014, 29(1):428-439.

[19]徐升, 房建成, 郑世强. 控制力矩陀螺悬浮转子的指数趋近积分滑模控制研究[J]. 宇航学报, 2014, 35(4):339-446.Xu Sheng, Fang Jian-cheng, Zheng Shi-qiang. Research on integral sliding mode control with exponential approximation law for magnetically suspended rotor system of CMG[J]. Journal of Astronautics, 2014, 35(4): 339-446.

[20]Chapel1 J, Stancliffe D, Bevacqua T, et al. Guidance,navigation, and control performance for the GOES-R spacecraft[C]//CEAS Space Journal, 2015, 7(2): 87-104.

[21]Grassidis J L, Junkins J L. Optimal estimation of dynamic systems[M]. Second edition. New York: CRC Press, 2012.391-399.

[22]孙羽佳, 袁利, 雷拥军. 基于指令力矩螺旋式搜索的SGCMG奇异规避方法[J]. 空间控制技术与应用, 2016,42(6): 26-30.Sun Yu-jia, Yuan Li, Lei Yong-jun. SGCMG singularity avoidance method based on command torque vector helix search[J]. Aerospace Control and Application, 2016, 42(6):26-30.

[23]Ting Hao, Matunaga S, TSUBAME development team. A practical attitude control system using control moment gyros for nano-satellite TSUBAME[C]//53rd AIAA Aerospace Sciences Meeting. Kissimmee, Florida, 2015.

[24]Zhang Hui-juan, Fang Jian-cheng. Robust backstepping control for agile satellite using double-gimbal variablespeed control moment gyroscope[J]. Journal of Guidance Control and Dynamics, 2013, 36(5): 1356-1363.

[25]Stevenson D, Schaub H. Nonlinear control analysis of a double-gimbal variable-speed control moment gyroscope[J]. Journal of Guidance Control and Dynamics, 2012,35(3): 787-793.

[26]Kusuda Y, M.takahashi M. Design of feedback control system using nominal inputs for satellite attitude maueuver using control moment gyros[C]//AIAA Guidance,Navigation, and Control Conference. Chicago, Illinois,2009. AIAA-2009-6205.

[27]Wright J W. Advancements of in-flight mass moment of inertia and structural deflection algorithms for satellite attitude simulators[D]. PhD Thesis. Ohio: Air Force Institute of Technology, 2015.

[28]Karpenko M, Ross M. Implementation of shortest-time maneuvers for genoric CMG steering laws[C]//AIAA/AAS Astrodynamics Specialist Conference. Minneapolis.Minnesota, 2012.

High-precision attitude control method based on MSCMG for large-scale remote sensing satellite

SHU Shi1,2,3, FANG Jian-cheng1,2,3, ZHANG Wei4, LIU Gang1,2,3, QIAN Yong4, FANG Bao-dong4, LIU Hu1,2,3
(1. School of Instrument Science and Opto-electronics Engineering, Beiing University of Aeronautics and Astronautics,Beijing 100191, China; 2. Novel Inertial Instrument & Navigation System Technology Key Laboratory of Fundamental Science for National Defense, Beijing 100191, China; 3. Inertial Technology Key Laboratory, Beijing 100191, China;4. Shanghai Institute of Satellite Engineering, Shanghai 200240, China)

Focusing on the complexity and precision problem of the feed forward and closed-loop feed backward system of large-torque flywheels, a high-precision attitude control method based on magnetically suspended control moment gyros (MSCMG) is proposed for large-scale remote sensing satellite. The MSCMG is used as actuator mechanism of the control system and applied into the camera movement compensation system of remote sensing satellite. Based on the control law design of variable-structure feedback compensation, a novel motion compensation control system is established to reduce the coupling between the camera and the platform. The characteristics of the MSCMG, such as large torque, small inverse excitation and high precision, are analyzed and applied into the motion compensation control system of the ground remote sensing imaging camera. Simulation results show that, compared with the traditional flywheel feed forward compensation, the platform stability by the proposed MSCMG-based method is increased by an order of magnitude, and the attitude stability as well as the image quality is effectively improved. The research results can be used as references for the development of the very high precision satellite attitude control and the payload movement compensation.

remote satellite; magnetically suspended control moment gyros (MSCMG); camera motion;feed- back compensation; high-precision attitude control

1005-6734(2017)04-0421-11

10.13695/j.cnki.12-1222/o4.2017.04.001

V488.2

A

2017-04-05；

2017-07-26

国家“973”计划（2014CB744200）；国家“973”计划（2013CB834103）

舒适（1973—），男，博士研究生，从事惯性导航与控制技术研究。E-mail: shushi509@icloud.com

联 系 人：房建成（1965—），男，教授，博士生导师，从事惯性导航与控制技术研究。E-mail: fangjiancheng@buaa.edu.cn