采用空间编码与正弦选择算子遗传算法求解排课问题∗

钱海军

（珠海城市职业技术学院 珠海 519000）

采用空间编码与正弦选择算子遗传算法求解排课问题∗

钱海军

（珠海城市职业技术学院 珠海 519000）

遗传算法是求解多约束、多目标组合优化问题的有效算法。经典遗传算法具有早熟特性，可以直接导致算法陷入局部最优解。为了提高算法的全局搜索性能，以遗传算法的染色体编码设计和选择算子设计两个方面为切人点，提出基于空间编码与正弦选择算子遗传算法（SCSS）。仿真实验证明，SCSS遗传算法求解开放教育排课问题能够满足多重约束条件，为有效实现排课问题的智能求解提供实用性的数学方法。改进后的遗传算法能够快速收敛得到问题的全局最优解，算法全局搜索性能明显增强。

遗传算法；多约束；空间编码；正弦选择算子；开放教育；全局最优解

1 引言

由美国Michigan大学Holland教授于1975年首次提出的遗传算法［1］是求解最优化问题的经典方法之一［2］。该算法对于非线性、大规模、单峰函数、多峰多态函数的求解都可以获得较好的结果。遗传算法是一种模拟自然选择、物种进化的全局优化搜索技术。其优点是采用种群搜索技术在解空间进行全局搜索以获得全局最优解。遗传算法通过对种群随机产生的一组个体进行选择、交叉、变异三种遗传算子实现种群进化。选择算子是根据个体适应度值来确定个体进行交叉和变异操作，适应度值高个体的则被选择进行迭代进化，反之被淘汰；借助生物种群遗传信息的概念，交叉算子通过染色体编码在整个解空间进行有效搜索，将选择的父代个体进行基因重组，交换两个个体的基因座，从而产生大量的新个体。交叉的过程能够增强最优个体的出现几率，提高全局搜索能力的同时降低对有效模式的破坏概率。变异算子是通过模拟生物遗传和进化过程中的变异环节实现对个体的变异，这个过程是新个体产生的重要原因之一［3］。变异算子在交叉算子的基础上对产生的新个体内部基因进行微调，维持种群的多样性［4］，使算法还具有一定的局部搜索能力。

2 算法改进

实践证明，经过一定的迭代之后，种群的多样性将有所降低，遗传算法出现过早收敛［5］，较容易产生局部最优解。国内外学者针对算法内部的每个环节进行了大量研究，并提出了诸多有效地改进方法［6～8］。本文在借鉴上述研究成果的基础上，从染色体编码方式与选择算子改进两个方向为切入点，提出一种改进的遗传算法。

2.1 三维空间编码设计

通过分析，经典的遗传算法采用二进制染色体编码方式，在变异操作过程中，二进制编码的各个基因座权重不同，导致变异的基因座越靠向高位，编码串的改变量越大，则变异后越容易丢失最优个体［9］。本文基于经典遗传算法的原理，结合开放大学远程开放教育教学特征与排课问题的数学模型，提出基于三维空间的遗传算法染色体编码方案。

2.1.1 排课问题数学建模［10］

1）根据开放教育教学特征，建立排课问题数学模型，假设：

教师集合 Professors=｛J1，J2，…，Jm，…，JM｝，其中，1≤m≤M ；

教室集合 Classrooms=｛R1，R2，…，Rp，…，RP｝，其中，1≤p≤P；教室可容纳人数Y；

课程集合 Courses=｛C1，C2，…，Cs，…，CS｝，其中，1≤s≤S；

时间集合 Times=｛T1，T2，…，Tq，…，TQ｝，其中，1≤q≤Q；

班级集合 Stugroups=｛G1，G2，…，Gn，…，GN｝，其中，1≤n≤N ；班级人数X=｛x1，x2，…，xn，…，xN｝；

2）排课问题属于一种非线性、资源时空组合问题，建立硬约束条件［11］，如表1所示。

表1 远程开放教育排课问题硬约束条件

3）建立排课问题软约束条件［11］。

S1：教学效果较好的时间段安排较重要的课程，可以有效提高教学质量。开放教育教学安排的一般在周一至周五晚上，周六、周日全天。由于成人参与学习的特点，可以认为到课率较高的时间，教学效果也较好。数据分析可知，除周末外，教学质量较好的时间序列为：星期一、星期四、星期二、星期三、星期五。

假设 αi(i=1，2，3，4，5)表示授课时间段的优先级；数学描述如表2所示。

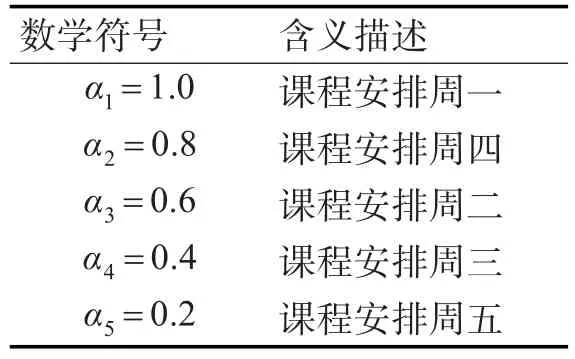
表2 S1软约束条件变量

假设 βj(j=1，2，3，4，5，6)表示课程重要程度，其中：“1”表示通识课，“2”表示专业拓展课，“3”表示综合实践、“4”表示专业课，“5”表示专业基础课，“6”表示公共基础课。则优化目标为

S2：满足部分教师提出的课程安排的要求。假设职称的级别系数为 εi(i=1，2，3)，“1”表示高职职称，”2”表示中级职称，”3”表示初级职称；教师在规定时间段上课的意愿程度系数为δj(j=0，1，2)，其中“2”表示愿意，“1”表示可以接受，“0”表示不愿意；则优化目标为

S3：多学时课程授课时间应保证一定的间隔时间。假设一门课程的授课时间间隔为i天的教学效果系数为 λi(i=1，2，3，4，5)，设定1，2，3，4，5天的系数值分别为1，4，5，3，2，βj为课程的权重。则优化目标为

S4：同一课表，班级课程安排尽量保证均匀分布。某班级周课时分布均匀程度为

其中，ed表示班级GN在第d周上课的课时数，N表示班级的总数，则优化目标为

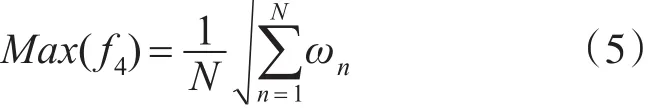
S5：教室利用率最大化，即根据班级学生的人数分配教室。假设班级人数XN与教室可容纳的学生人数为YS的比值等于1，则教室利用率越高。约束条件优化目标为

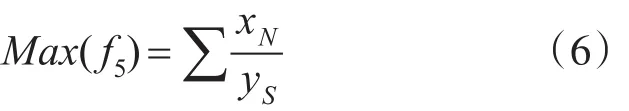
2.1.2 染色体编码设计

开放教育专业规划能够确定排课问题数学模型中的教师集合Professors、课程集合Courses与班级集合Stugroups。作为已知参数，三个集合可以被组合成一个课程元祖，用 CPS（Courses、Professors、Stugroups）描述。如图1所示，空间三维坐标体系内，X轴为T（时间片），坐标值对应一周内11个教学时间段，即 X1～X11；Y轴为 R（教室），坐标值对应学校全部可用的教室总数R，即Y1～YR；Z轴代表一个课程元组CPS。

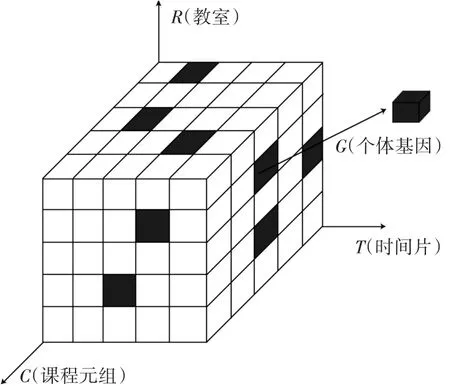
图1 三维空间染色体编码方案

从图1可以看出，由空间三维坐标构成的黑色小立方体可以确定一个课程基因，该课程基因表示在某授课时间片TQ，某班级GN，在教室RP安排课程CS的授课事件。全部课程基因组成一条染色体，即表示一个课程表的排课方案。在时间片TQ和教室RP确定的条件下，课程基因（授课事件）数为

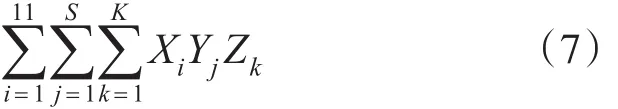
为了较直观地描述该三维空间染色体编码方案，将课程基因总数的求解映射为一个三维数组Timetable[][][]=｛(JM，GN，CS)，TQ，RP｝，图形化描述该数据结构如图2所示。

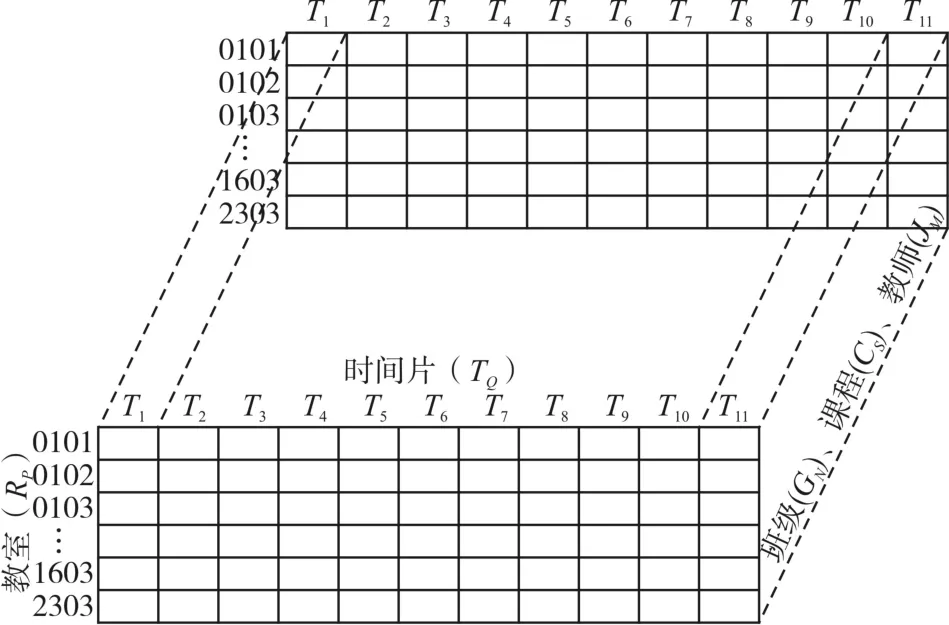
图2 图形化编码方案

具体的染色体编码设计采用十进制编码。三位数组中的各数组元素按照表5、表6所示的时间模式编码表、教室编码表和班级编码表，分别映射成为十进制数表示相应的排课信息。

1）时间模式编码表及含义

表5 时间模式编码表

模式编码表中的星期一至星期日分别用十进制数1～7表示；每天有3个教学时间段，分别用1～3表示。考虑到开放教育教学安排的特殊性及多学时课程的教学特点，实际时间段的编码再添加4位数字位，共6位十进制数表示某课程的教学时间段，并能够从该编码中直接获取该课程的学时数。例如：编码430000表示该课程在每周四晚上上课；编码235300表示该课程每周二晚上和周五晚上上课；编码136273表示该课程每周一晚上、周六下午和周日晚上上课。

2）教室编码表及含义

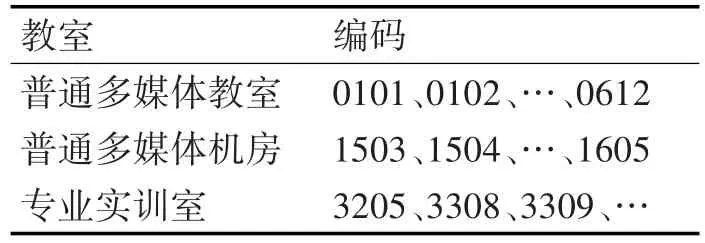
表6 教室编码表

教室编码第1位用来区分教室类型，“0”表示普通教室，“1”表示多媒体机房，“2”表示专业实训室；第2～3位为教室按照楼层的流水号。因为学校仅有一幢教学楼，所以教室编码不涉及跨区域教室。

3）班级编码

开放教育实行春、秋两季本、专科同时招生。按照学校开放教育的实际情况，以专业作为划分班级的最基本单位。班级编码由“入学年度”、“专业代码”、“区分位”三个标识位组合而成。例如：编码201520111表示2015级工商企业管理专科；具体各专业代码可提前进行预编码处理。

2.2 适应度函数设计

适应度函数应满足规范性、单值、连续，计算简单，通用性较好等特性。分析可知，适应度函数值是非负的，任何情况下越大越好。目标函数O(x)与适应度函数值Fit(x)之间的关系存在映射问题，即当求O(x)最大值点时，O(x)与Fit(x)的变化方向相同；当求O(x)最小值点时，O(x)与Fit(x)的变化方向相反，此时目标函数值越小，适应度函数值则越大。排课问题的求解依赖于多目标优化，即满足多个硬约束条件与尽量多的软约束条件，达到资源分配的最优化。本文提出加权约束适应度函数模型，即：

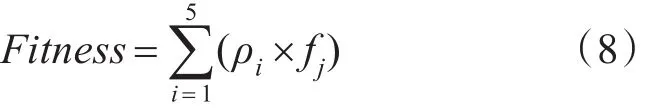
2.3 初始化种群

算法初始化为后续选择算子、交叉算子、变异算子提供基础染色体群。经典的遗传算法通过随机搜索的方式［12］产生初始种群。这些随机产生的初始种群在可行解空间上会出现较均匀的散步与较集中的聚集两种极端情况。

1）随机搜索法

本文通过一维多峰函数对初始种群的随机搜索方式进行测试，进一步说明这种由随机搜索方式产生的初始化种群对遗传算法的影响。

例如一维多峰函数

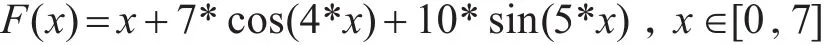
在解的表示方式、初始种群规模、算子、算法终止条件等算法控制参数相同的情况下求解该函数的最大值，以此观察随机搜索产生的初始化种群对遗传算法的计算结果的影响。通过Matlab求解得到图3计算结果。

图3 一维多峰函数测试结果

图3 （a）、（b）分别为采用同一随机搜索方式产生经过20次迭代产生初始化种群的遗传算法程序计算结果。图3（b）显示，经过种群迭代，随机搜索方式产生的个体呈现小范围集聚，且略微偏向左侧，导致算法计算结果较早收敛，形成局部最优。分析可知，在遗传算法的遗传代数与算子一定的情况下随机搜索方式产生的初始种群会引起遗传算法的不稳定的计算结果。

2）可行解空间网格划分法

随机搜索法产生的初始化种群在均匀散步的状态下具有较高的多样性，经过遗传算子操作收敛于全局最优解可能性较大；但同时，随机搜索产生的分布集中的初始种群会较集中地落在某些子空间中，从而导致遗传操作收敛到子空间的局部最优解，算法搜索产生停滞，搜索空间无法扩大，算法无法收敛到最优解［11］。由于随机搜索法产生的种群适应度较低，且具有不稳定性质。为了能够提高初始种群的群体适应度，本文运用空间网格划分法产生初始化种群。具体步骤如下：

步骤1：将目标空间进行网格化划分。参考点落入可行解空间的所有网格，且将每个网格作为一个参考对象。根据种群的规模控制参考点的数量，通过参考点的组合求解多目标优化的可行解。

步骤2：在可行解空间，将m维向量构成的目标空间划分为k等份。这样得到m*k个目标子空间，k的值根据计算精度要求与可行解空间的大小进行设定。m*k个目标子空间对应k˄m可行解子空间，产生k˄m个网格。

步骤3：将每个网格映射为个体目标函数值，可以得到初始种群数为k˄m。

步骤4：设某个体目标函数的解空间为[Xmin，Xmax]，依二分法求均值的思路，在解空间搜索i个点，则目标函数值为

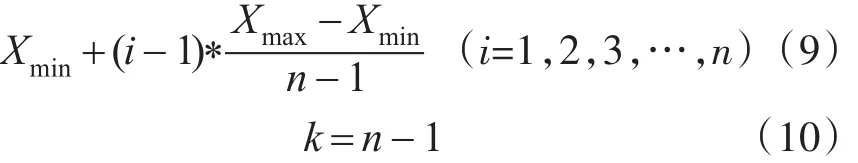
通过解空间网格化划分产生的初始点，包括全局最优点与局部最优点必然全部落在网格节点或者节点之间，种群进化搜索过程中，算法能够被较容易地搜索到最优点。这种方法产生的初始种群包含最优解组合的概率明显增强，且技术性地避免了相似个体的被选取，以减少种群数量。该方法与算法的选择、交叉、变异算子结合，可以提高算法搜索效率与收敛于全局最优解的概率。

2.4 选择、交叉、变异操作

经典遗传算法的选择策略是基于个体适应度的比例择优选择策略。设计的选择算子不同将导致个体不同的选择概率，从而产生的种群亦有不同。传统选择排序算子的概率值依据经验设定，适应度概率较高的个体会以较高的概率进化到下一代种群当中，但同样也存在被淘汰的情况；轮盘选择方法则无法处理个体适应度值非负数的情况，通用性较差。而在排序选择方法中，概率分布无规律可循，容易引起局部收敛［13］，造成算法搜索缓慢的问题。

2.4.1 正弦选择算子

本文提出一种基于最优个体保留策略的正弦函数选择算子，可以有效提高算法的搜索精度。改进的选择算子选择策略分两步进行。

步骤1：基于个体适应度值，将当前代种群中适应度最高的个体直接复制到下一代。假设第k代最优个体为 Amax(k)，第 k+1代最劣个体Amin(k+1)。保留Amax(k)，并直接替换Amin(k+1)，Amax(k)不参与交叉、变异遗传操作。第k+1代的种群数为

SA(k+1)=SA(k+1)+Amax(k)-Amin(k+1)

步骤2：对当前代（第k代）种群的其它个体采用改进的正弦函数选择算子进行选择与复制操作 。 根 据 正 弦 函 数 f(θi)=sin(θi) 的 特 性 ，当θ ∈[0，π]，f(θ)在 [0，1]区间呈现单调递增。假设种群个体的适应值为 f1，f2，…，fn，fi∈[fmin，fmax]，i=1，2，...n 。 将 fi∈[fmin，fmax] 等 比 例 映 射 到θ∈[0，]，则可以设计选择概率：

μ为比例调节系数，作用是保证选择概率在［0，1］区间内均匀分布，降低产生偏差的几率。

步骤3：结合轮盘赌选择方法进行选择运算。

2.4.2 自适应交叉算子［14］

经典遗传算法会由于进化过程中交叉概率Pc和变异概率Pm保持不变导致算法性能的下降。依据经验知识与算法规则可知，在种群迭代初期，设置较大的交叉概率能够明显增强算法的搜索能力；在种群迭代后期，交叉概率设定小一点则可以有效避免优良基因被淘汰，从而加快算法的收敛［15］。为了提高算法的性能，降低最优个体（适应度高）被淘汰的几率，本文应用最优个体保留策略，最优个体被保留，不参与交叉和变异操作，剩余个体参与交叉和变异操作，防止陷于局部最优。采用自适应交叉概率为

其中，C1为调解系数，其值为（0，1）的随机数，通过在计算机程序中设置rand随机函数产生；C2为（0，1）之间的常量；fmax表示种群当前代t中的最优个体适应度函数值；favg表示t中个体的平均适应度函数值；fc表示经过交叉操作的个体中适应度函数值的最大值。

2.4.3 自适应变异算子［14］

种群个体具备的基因差异性对于整个种群的进化的起着至关重要的作用。优良个体之间的基因基因重组可以保证进化过程中种群的优良基因被保留下来，基因较差的个体则会被淘汰，这就是优胜劣汰的选择过程。可以对种群中不同个体设定不同的变异概率。对于种群中的优良个体，设定较小的变异概率，从而保证优良个体通过交叉操作后能够，优良基因被保存和累积；对于种群中的较差个体，设定较大的变异概率，通过交叉操作增强种群的搜索能力［16］。基于上述分析，算法的变异操作采用自适应变异概率以提高种群的多样性，增强算法维持搜索的能力。在种群迭代初期，自适应概率能够在个体性能较差的条件下，造成较大的扰动来扩大算法的解空间；随着迭代次数的增加，自适应变异概率能够逐步减少成为一个0～1之间的常量，以保证算法的平滑收敛。采用自适应变异概率为

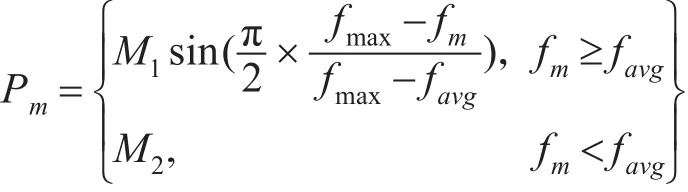
其中，M1为调解系数，其值为（0，1）的随机数，通过在计算机程序中设置rand随机函数产生；M2为（0，1）之间的常量；fmax、favg含义同上；fm表示经过交叉操作的个体中适应度函数值的最大值。

3 仿真实验

课程编排可以归结为教学资源分配的数学问题［17～18］。排课问题被证明是一种NP问题［19］。遗传算法的整体搜索策略与求解优化设计对求解问题类型具有较强鲁棒性，即算法本身的搜索策略与求解优化技术不依赖于具体求解问题所涉及的领域知识［20］，仅在算法进化过程中，对问题的目标函数求解方向与适应度函数有所影响。本文以某开放大学2015年秋季的排课数据作为算法训练样本求解排课问题。数据集如表7所示。

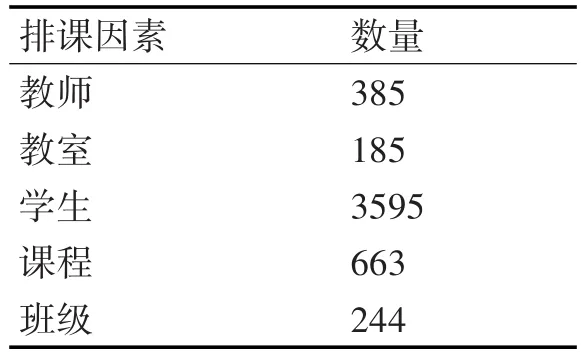
表7 训练数据集

3.1 Matlab仿真参数设置

本文利用Matlab遗传算法工具箱，编写仿真程序对表7数据集进行训练。在提出的改进遗传算法中，交叉概率Pc与变异概率Pm具有自适应性，故无需设置。其他参数设置如下：

1）仿真实验中，种群规模过小会导致目标函数值产生较大的波动；种群过大则可能造成收敛时间较多，消耗资源。NIND表示种群规模，本文设置为200。

2）MAXGEN表示最大遗传代数，该参数过大会导致过早收敛，无法搜索到全局最优解。根据训练样本的数量，本文设置为800。

3.2 Matlab仿真结果

算法仿真实验中，利用本文提出的空间编码与正弦选择算子遗传算法（SCSS）与Pillay N等［21］提出的改进遗传算法进行适应度函数值对比。

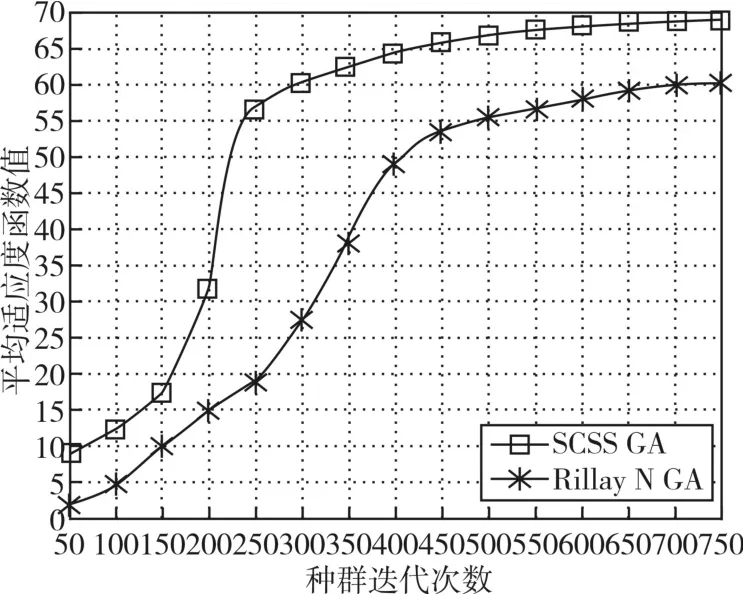
图4 两种遗传算法适应度函数值对比

实验中，种群每迭代50代就记录一次种群适应度函数值，共记录15次。通过计算15次记录的最佳适应度函数值的平均值，得出图4所示的实验结果。从结果可以看出，本文提出的SCSS遗传算法能够较好地解决开放教育排课问题。

4 结语

本文提出的基于空间编码和正弦选择算子遗传算法—SCSS，从算法性能和早熟收敛两个方面对经典遗传算法进行了改进。基于三维空间染色体编码可以有效增强种群多样性。在选择算子的非线性变换中加入正弦三角函数，改善了算法的收敛性能。通过采用SCSS仿真求解开放教育排课问题，进一步验证了SSCS遗传算法具有较好地全局收敛性。

［1］J.H.Holland.Adaptation in natural and artificial systems［M］.Ann Arbor：The University of Michigan Press，1975.08-30.

［2］De Jong，Kenneth Alan.An analysis of the behavior of a class of genetic adaptive systems［D］.Michigan：University of Michigan，1975.05-35.

［3］周明，孙树栋，等.遗传算法原理及应用［M］.北京：国防工业出版社，1999.11-13.ZHOU Ming，SUN Shudong，et al.Genetic algorithm：Theory and Application［M］.Beijing：National Defence Industry Press，1999.11-13.

［4］Muehlenbein H.How genetic algorithms really work：mutation and hill climbing［C］//In Proc，and Workshop Parallel Problem Solving from Nature，1992：15-25.

［5］刘红，韦穗.遗传算子的分析［J］.计算机技术与发展，2006，16（10）：80-82.LIU Hong，WEI Hui.Analysis on Genetic Operators Computer［J］.Technology and Development，2006，16（10）：80-82.

［6］Ichikawa Y，Ishii Y.Retaining diversity of genetic algorithms for multivariable optimization and neural network learning［C］//Proc of IEEE international conference on neural net-work.［s.l.］：［s.n.］，1993：1110-1114.

［7］Srinivas M，Patnaik L M.Adaptive probabilities of crossover and mutation in genetic algorithm［J］.IEEE trans on systems，man and cybernetics，1994，24（4）：656-667.

［8］杨启文，蒋静坪，张国宏.遗传算法优化速度的改进［J］.软件学报，2001，12（2）：270-275.YANG Qiwen，JIANG Jingping，ZHANG GUOhong.Improved Optimization Speed for Genetic Algorithms［J］.Journal of Software，2001，12（2）：270-275.

［9］郑生荣，赖家美，刘国亮，等.一种改进的实数编码混合遗传算法［J］.计算机应用，2006，26（8）：1959-1962.ZHENG Shengrong，LAI Jiamei，LIU Guoliang，et al.Improved real coded hybrid genetic algorithm［J］.Computer Applications，2006，26（8）：1959-1962.

［10］钱海军.开放教育排课问题约束分析与数学建模［J］.软件工程，2016，19（9）：27-29.QIAN Haijun.Constraint Analysis and Mathematical Modeling in the Open Education Timetabling［J］.Software Engineering，2016，19（9）：27-29.

［11］Shi Juan.Research on application of IGA（Immune Genetic Algorithm）to the solution of course-timetabling problem［C］//Proceedings of 2009 4th International Conference on Computer Science and Education，Nanning，China，2009：1105-1109.

［12］Guyon O，Lemaire P，Pinson*.Cut Generation for an Inte-grated Employee Timetabling and Production Scheduling Problem［J］.European Journal of Operational Research，2010，201（2）：557-567.

［13］Pandey H M，Chaudhary A，Mehrotra D.A comparative Review of Approaches to Prevent Premature Convergence in GA［J］.Applied Soft Computing，2001，24：1047-1077.

［14］朱灏东，李红婵.采用三维小生境遗传算法求解高校排课问题［J］.计算机工程与应用，2011，47（34）：242-245.ZHU Haodong，LI Hongchan.Three-dimensional niche GA used to solve University Timetabling Problem［J］.Computer Engineering and Applications，2011，47（34）：242-245.

［15］马清亮，胡昌华，陈新海.遗传算法交叉和变异操作的模糊优化［J］.计算机工程与应用，2002，38（19）：33-34.MA Qingliang，HU Changhua，CHEN Xinhai.Fuzzy Optimization of Crossover and Mutation Opertion in Genetic Algorithm［J］.Computer Engineering and Applications，2002，38（19）：33-34.

［16］熊军，高敦堂，都思丹，等.变异率和种群数目自适应的遗传算法［J］.东南大学学报（自然科学版），2004（34）：553-556.XIONG Jun，GAO Duntang，DU Sidan，et al.Genetic algorithm with mutation probability and population size adaptation［J］.Journal of Southeast University（Natural Science Edition），2004（34）：553-556.

［17］Adewumi A O，Sawyerr B A，Montaz A M.A Heuristic Solution to the University Timetabling Problem［J］.Engineer-ing Computations，2009，26（8）：972-984.

［18］朱冠宇，王乘，席大春.利用遗传算法求解中学课表安排问题［J］.计算机工程与应用，2004（27）：215-218.ZHU Guanyu，WANG Cheng，XI Dachun.Genetic Algorithm for Solving Curriculum Schedule Problem of Senior High School［J］.Computer Engineering and Applications，2004（27）：215-218.

［19］Shi Juan.Research on Application of IGA（Immune Genetic Algorithm）to the Solution of Course-Timetabling Problem［C］//MProc of the 4th Int.l Conf on Computer Science and Education，2009：1109-1105.

［20］Detienne B，Péridy L，PinsonÉ.Cut generation for an employee timetabling problem［J］.European Journal of Operational Research，2009，197（3）：1178-1184.

［21］Pillay N，Banzhaf W.An Informed Genetic Algorithm for the Examination Timetabling Problem［J］.Applied Soft Computing，2010，10（2）：457-467.

Using a Space Coding and Sine Selection Operator GA to Solve the Timetabling Problem

QIAN Haijun
（Zhuhai City Polytechnic，Zhuhai 519000）

Genetic algorithm（GA）is an effective algorithm to solve multi-constrained and multi-objective combinatorial optimization problems.The classical genetic algorithm has the characteristics of premature convergence，which can lead to the local optimal solution.In order to improve the algorithm global searching performance，the paper proposed the genetic algorithm based on space coding and sine selection operator，or SCSS，taking the two aspects of chromosome coding design and selection operator design for the genetic algorithm as the cut-in point.The simulation results show that the SCSS genetic algorithm can solve the Open Education timetabling problem with multiple constraints，and provides a practical mathematical method to solve the problem of scheduling problem effectively.The improved genetic algorithm can quickly converge to the global optimal solution of the problem，and the global search performance of the algorithm is obviously enhanced.

genetic algorithm，multi-constrained，space coding，sine selection operator，the Open Education，the global optimal solution

TP301.6

10.3969/j.issn.1672-9722.2017.10.008

Class Number TP301.6

2017年4月17日，

2017年5月28日

2015年度广东省教育信息技术研究“粤教云”计划专项重点课题《基于兴趣簇的云流媒体系统模型的研究》（编号：2015YJYZ016）；2014年度广东远程开放教育科研基金项目《大数据视角下电大开放教育数据挖掘与分析对教与学的促进研究》（编号：YJ1418）资助。

钱海军，男，硕士，副教授，研究方向：系统理论，数据挖掘。