基于冲击模型的含间隙高速凸轮机构动力学分析

何雪明 - 何 楷 武美萍 - 纪小刚 -

(江南大学江苏省食品先进制造装备技术重点实验室，江苏 无锡 214122) (Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology, Wuxi, Jiangsu 214122, China)

基于冲击模型的含间隙高速凸轮机构动力学分析

何雪明HEXue-ming何 楷HEKai武美萍WUMei-ping纪小刚JIXiao-gang

(江南大学江苏省食品先进制造装备技术重点实验室，江苏 无锡 214122) (JiangsuKeyLaboratoryofAdvancedFoodManufacturingEquipmentandTechnology,Wuxi,Jiangsu214122,China)

为了提高含间隙高速凸轮机构动态性能。采用二状态冲击副模型模拟凸轮和从动件间的间隙，构建考虑阻尼的含间隙凸轮机构动力学模型。以摆线凸轮曲线为激振函数，采用有限差分法求解动力学方程。对含间隙动力学模型进行时域和频域分析，绘制相应的加速度时域和频域响应图谱，得出了阻尼比、周期比对动态响应的影响，并对常用的几种高速凸轮曲线进行动力学分析。得出：间隙存在会导致系统响应精度变差；间隙对从动件升程加速段的影响较小；对减速段和休止期影响较大；传统理论在间隙动力学中的应用存在局限性。

含间隙高速凸轮机构；动力学模型；时域分析；频域分析

凸轮机构由于其分度精度高、运转平稳、体积小等特点，在自动机械中被广泛应用，如洗瓶机、灌装机、自动包装机等[1-3]。高速凸轮机构广泛应用于内燃机、印刷、纺织等自动或半自动机械中。由于加工误差和磨损的影响，间隙的存在不可避免，另一方面，间隙可贮存润滑脂、降低温度对配合精度的影响，所以间隙的存在也是必要的。近年来，凸轮机构动力学动态特性逐渐被重视，并获得了大量新的研究成果。Senevirantne等[4]提出了模拟间隙的二状态冲击副模型，在动力学分析中广泛得到应用；郭杏林等[5-6]在考虑间隙情况下，对平面连杆机构进行分析；Koster等[7]在考虑间隙情况下，构建多自由度凸轮机构模型，取得了较好的研究效果；常宗瑜等[8-9]对含间隙凸轮机构进行试验研究，验证了以往动力学模型的正确性。本研究将多自由度含间隙高速凸轮机构等效简化为单自由度系统，并分析了阻尼、周期比和凸轮曲线对含间隙单自由度系统动态响应的影响。

1 含间隙凸轮机构横越冲击现象

凸轮机构运动时，因间隙的存在，从动件在凸轮槽中会发生失去接触的现象，待再次接触时会产生碰撞，引起剧烈振动，并产生噪声。碰撞时速度、加速度和接触力可能是无间隙状态下的几倍或者几十倍，是影响机械运转速度提高的关键因素之一。图1为几何封闭的移动凸轮：主动件凸轮左右运动，从动件上下运动。图1中的A、B为凸轮槽的2个面。在凸轮高速运转情况下，惯性载荷为整个机构载荷的主要部分，凸轮槽和从动件滚子之间仅有惯性载荷的作用。从动件升程中，速度先升后降，加速度先正后负。在加速阶段，从动件滚子与凸轮的A面接触；当加速度为零时，接触处的力消失；滚子以该瞬时的速度开始飞越槽中的间隙，与轮槽的B面碰撞，即横越冲击现象。为了详细研究间隙存在下的横越冲击现象，下面对横越冲击现象发生的原理及影响因素进行研究。

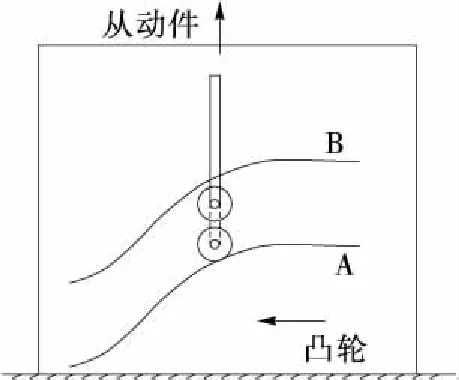
图1 凸轮机构横越冲击现象Figure 1 Cross impact on cam mechanism

从动件升程中，设在时间t=tm时，从动件加速度开始变化，此时速度达到最大值vmax，滚子以此速度离开A面与槽分离，从动件靠其惯性以速度vmax运动。设滚子穿越间隙所需时间为△t；则经过时间△t间隔在tm+△t时刻，从动件以直线运动到轮槽的B面上，此时凸轮在垂直方向的速度仍按预设从动件速度曲线变化，该瞬时的速度设为vc，从动件的速度仍可认为是vmax。则碰撞速度为：

vimp=vmax-vc。

(1)

将预设的从动件速度vc按泰勒级数展开：

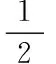
(2)

在t=tm时加速度及其速度为：a(tm)=0,v(tm)=vmax。

j(tm)为t=tm时刻预设从动件运行的跃度值，则可得碰撞速度可近似计为：

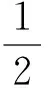
(3)

设间隙值为γ，穿越时间为△t，预设从动件的速度为v，则有：

(4)

将式(4)积分后的位移用泰勒级数展开有：

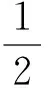
(5)

因为a(tm)=0,v(tm)=vmax，所以式(5)可化简为：

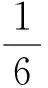
(6)

可得：

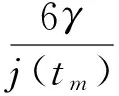
(7)

将式(7)代入式(3)，可得碰撞速度为：

(8)

将式(8)无因次化处理可得无因次碰撞速度Vimp为：

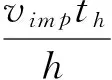
(9)

式中：

h——从动件升程总位移，m；

th——升程周期，s。

无因次跃度值为：

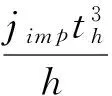
(10)

将式(9)、(10)代入式(8)可得：

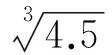
(11)

式中：

Γ——无因次化处理后的间隙，m。

Γ计算公式见式(12)。

(12)

分析式(11)可得影响横越冲击现象碰撞速度的主要因素有：

(1) 凸轮槽的间隙值。碰撞速度随间隙的增大而增大，因此控制凸轮槽的公差及磨损。

(2) 加速度变化点的跃度值。碰撞速度与加速度变化点的跃度值的立方根呈正比，因此对几何封闭高速凸轮设计时，要对凸轮曲线加速度变化点附近的跃度值进行计算，以便减小间隙引起的横越冲击现象的碰撞速度。

2 含间隙凸轮机构动力学模型

对于含间隙凸轮机构动力学研究采用如下研究方法，首先构建动力学模型，建立相应动力学方程，再求解，分析结果。构建含间隙的动力学模型，需要对间隙进行模拟，模拟的方法很多，此处采用Dubowsky二状态冲击副模型模拟间隙，将该模型引入到动力学模型中，建立含间隙动力学模型。最后根据该模型建立相应的方程，进行求解计算。

二状态冲击副模型将运动副元素之间的关系分为分离和接触变形2种状态，具体模型见图2。在运动过程中，运动副元素交替处于接触和自由2种状态，计入运动副元素的接触表面弹性和阻尼。当-γ≤x-s≤γ时，从动件处于自由振动状态，此时凸轮和从动件间的接触力为0；若x-s≥γ或者x-s≤-γ时，凸轮和从动件接触，这时阻尼和构件刚度开始起作用，产生接触力。综上可得到接触力变化趋势，见图3。

将二状态冲击副模型引入到凸轮机构动力模型，见图4，可得含间隙凸轮机构动力学模型。因为实际工况中凸轮和从动件间的阻尼系数(c1)一般远小于从动件和机架间的阻尼系数(c)，为了计算简便，忽略凸轮和从动件间的阻尼系数(c1)，只考虑机架间的阻尼系数(c)。根据含间隙动力学模型，对机构进行力学分析可得含间隙动力学方程，见式(13)。

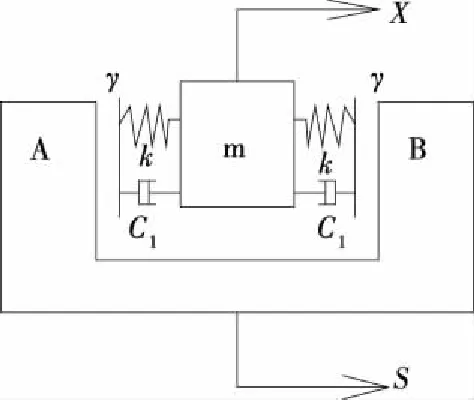
m. 凸轮从动件 A、B. 分别为凸轮槽的两端γ. 轮槽与凸轮从动件间的间隙s. 预设的从动件运动规律x. 从动件实际响应的运动规律k. 凸轮和从动件之间的接触刚度系数C1. 凸轮和从动件之间的阻尼比

图2 二状态冲击副模型

Figure 2 Two states impact pair model

图3 接触力变化Figure 3 The variation of contact force

图4 含间隙动力学模型Figure 4 Dynamic model with clearance

(13)

式(13)中f(x-s)表达式为：

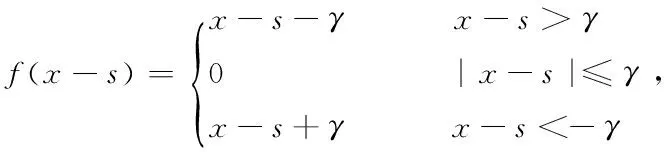
(14)

式中：

x——从动件实际运动位移，m；

s——从动件理想运动位移，m；

k——系统的等效刚度，N/m；

m——系统的等效质量，g；

c——从动件与机架阻尼系数。

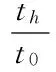
(15)

式中：

h——从动件升程总位移，m；

th——升程周期(反映了凸轮的转速)，s；

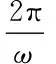
联立式(13)、(15)，可得无因次含间隙动力学方程见式(16)。

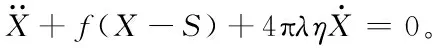
(16)

式(16)中f(X-S)表达式见式(17)。

(17)

3 动力学方程有限差分法求解

摆线凸轮曲线因其良好的动力学性能，在中高速凸轮中广泛应用，现以摆线凸轮曲线作为例子，对凸轮机构的动力学响应进行分析，摆线凸轮曲线的无因次位移方程见式(18)。

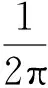
(18)

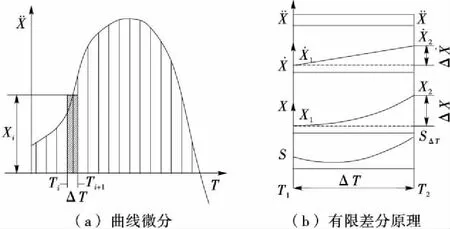
图5 有限差分法数学模型Figure 5 Mathematical model of finite difference method

(19)

(20)

(21)

X2=X1+△X。

(22)

系统总响应方程式(16)可改写为式(23)：

(23)

式(23)位移增量可由式(24)表示：

(24)

速度增量可由式(25)表示：

(25)

将式(24)、(25)代入式(23)可得：

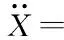
(26)

采用有限差分法求解上节动力学方程，有限差分法求解动力学方程的计算机求解流程见图6。

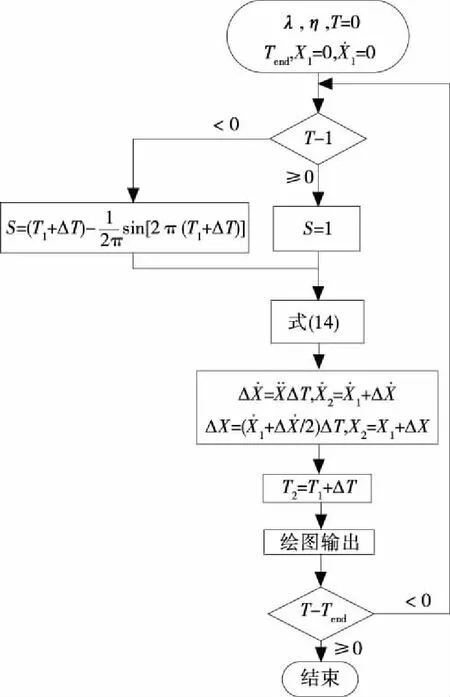
图6 有限差分法计算流程Figure 6 Calculation flow of finite difference method

4 含间隙高速凸轮机构动力学分析

4.1 含间隙高速凸轮机构时域分析

由图7～8可知，在主振动阶段，一方面随着阻尼的增大，间隙横越冲击现象越弱，这时阻尼减小了从动件和凸轮间的相对速度，从而消耗一部分碰撞能量，对构件起到了一定的保护作用。另一方面阻尼的存在又使运动发生滞后性，与前面研究是一致的。在残余振动阶段，阻尼可以削减主振动留下的能量，减小残余振动阶段从动件横越冲击次数和振幅，有利于凸轮机构进入休止期的平稳性。

因此阻尼除了具有无间隙动力学分析的优缺点外，在含间隙凸轮机构中还具有削弱横越冲击现象的优点，对于大周期比系统可以适当地增大阻尼以减小间隙的影响。总之，不管是在无间隙凸轮机构还是含间隙凸轮机构，阻尼都是一个重要的参数，在设计时必须慎重考虑，权衡其优缺点。

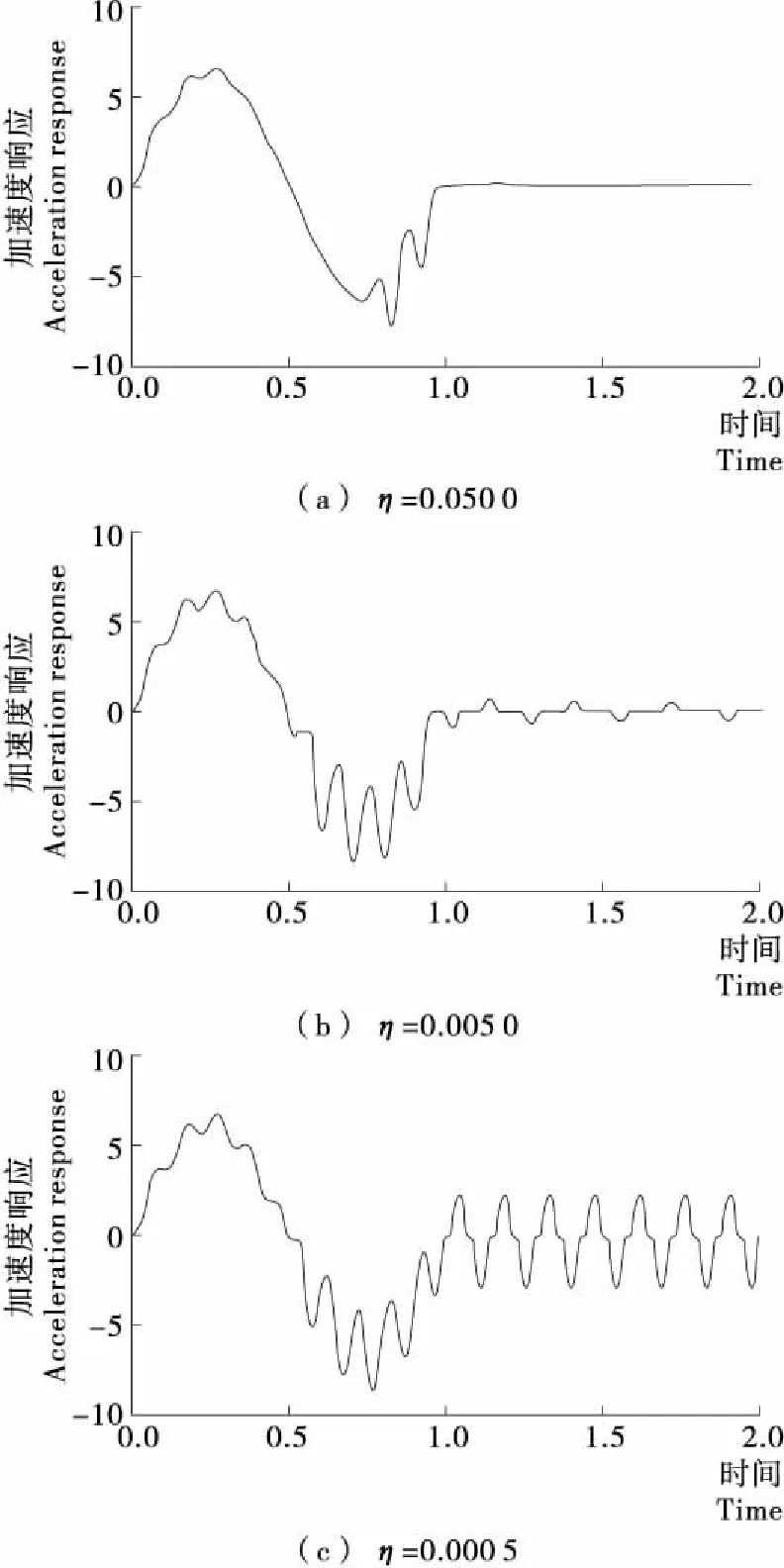
图7 不同阻尼比摆线加速度响应Figure 7 Cycloidal acceleration response with different damping ratio

图8 不同阻尼比摆线加速度响应误差对比Figure 8 Error comparison of cycloidal acceleration response with different damping ratio

4.2 含间隙高速凸轮机构频域分析

为了考查阻尼对含间隙凸轮机构运转平稳性的影响，确定凸轮机构合适的转速范围，对含间隙凸轮机构进行频域分析，在无因次间隙Γ=0.001情况下，分别绘制阻尼比η=0.500,0.050,0.005，加速度频域响应图谱，见图9。

由图9可知，无论是主振动阶段还是残余振动阶段，周期比较小时，加速度的频域响应呈现无间隙状态下的波浪式衰减规律，但当周期比增大后，响应振幅没有继续衰减，而是呈现无序性波动，有的周期比的响应振幅甚至比小周期比状态下都大，由此可得间隙对大周期比凸轮机构影响较大，与上节时域分析结果是一致的。另外，阻尼在一定程度上减小间隙横越冲击现象，减小振幅变化规律的无序性。

5 凸轮曲线对含间隙凸轮机构动态响应影响

前面以摆线凸轮曲线作为算例，对含间隙凸轮机构进行了频域和时域分析，为了更好地研究不同凸轮曲线在含间隙凸轮机构中的动力学响应特性，在阻尼比η=0.05，周期比γ=5，无因次间隙Γ=0.001情况下，选取几种有代表性的高速凸轮常用的凸轮曲线进行研究，其时域和频域响应图谱见图10～13。

图9 不同阻尼比摆线加速度频域响应Figure 9 Frequency response of cycloidal acceleration with different damping ratio

为了方便对比分析，选取主振动阶段加速度最大响应误差和残余振动阶段加速度最大振幅作为评价响应精度的特性参数，具体计算值见表1。

通过对图10～13及表1分析可得，不同凸轮曲线在含间隙凸轮机构中动力学响应差距较大，但在无间隙凸轮机构中动力学性能较好的，在含间隙凸轮机构依然表现出良好的性能。在以上所考查的凸轮曲线中，盖特曼1-3凸轮曲线的动力学响应精度较差，摆线和标准多项式凸轮曲线较好。对于标准多项式凸轮曲线，随着次数的升高，残余加速度最大振幅逐渐减小，也就是越能平稳进入休止期，从这点来说，传统对于多项式两端可导次数越高，凸轮动力学性能越好的理论是正确的。但是对于主振动阶段加速度响应最大误差并未随着两端可导次数的升高而下降，可见传统理论在间隙动力学中是存在局限的。

图10 3-4-5多项式凸轮曲线时域响应和频域响应Figure 10 Time domain response and frequency domain response of 3-4-5 polynomial cam curves

图11 4-5-6-7多项式凸轮曲线时域响应和频域响应Figure 11 Time domain response and frequency domain response of 4-5-6-7 polynomial cam curves

图12 5-6-7-8-9多项式凸轮曲线时域响应和频域响应Figure 12 Time domain response and frequency domain response of 5-6-7-8-9 polynomial cam curves

图13 盖特曼1-3凸轮曲线时域响应和频域响应Figure 13 Time domain response and frequency domain response of 1-3 polynomial cam curves

6 结论

(1) 间隙存在会导致从动件在凸轮槽中发生横越冲击现象，导致系统响应精度变差。间隙变大使系统冲击变大，动力响应幅值变大，会使凸轮磨损加快。动力间隙的存在对大周期比系统的影响要比小周期比系统影响大，也就是说对低速、大刚度机构影响更为严重，周期比越大该现象越明显。

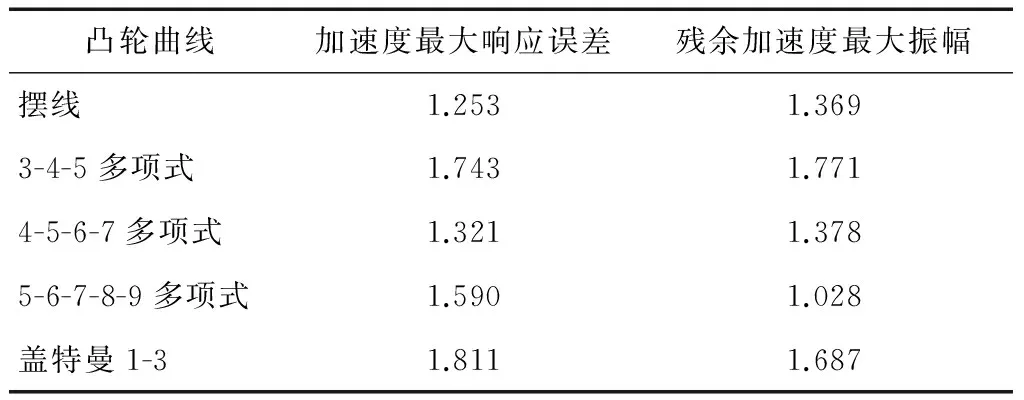
表1 凸轮曲线响应精度对比Table 1 Comparison of response accuracy of cam curves

增大阻尼可以减轻此现象，但阻尼使响应精度变差；阻尼的存在使主响应阶段动力学响应滞后，但可以加快残余振动阶段振动的衰减。

(2) 间隙对从动件升程加速段的影响较小，对减速段和休止期影响较大。间隙的存在使凸轮机构在大周期比状态频域响应呈现无序性，对该范围内运行的凸轮机构要进行动力学分析，确定合适的运行速度，以便使其运动更加平稳。

(3) 对常用的几种高速凸轮曲线进行动力学分析，结果发现，传统对于凸轮曲线应用的理论存在一定的局限性，为凸轮曲线选取提供一定的指导。

[1] 周文玲, 刘安静. 洗瓶机出瓶机构的设计分析[J]. 食品与机械, 2007, 23(2): 80-82.

[2] 余剑武, 舒新, 罗红, 等. 灌装机中弧面凸轮建模与造型研究[J]. 食品与机械, 2016, 32(6): 77-82.

[3] 韩炬, 王莹, 郭亚楠. 包装机热封机构的建模及动力学分析[J]. 食品与机械, 2013, 29(1): 146-148.

[4] SENEVIRANTNE L D, EARLS S W E. Chaotic behavior exhibited during contact loss in a clearance joint of a four-bar mechanism[J]. MMT, 1992, 27(3): 307-321.

[5] 郭杏林, 赵子坤. 含间隙柔性曲柄摇杆机构动力学分析[J]. 机械强度, 2010, 32(6): 905-909.

[6] 王国庆, 刘宏昭, 何长安. 含间隙连杆机构非线性行为研究[J]. 机械设计, 2005, 22(3): 12-34.

[7] KOSTER M P. Effect of flexibility of driving shaft on the dynamic behavior of a cam mechanism[J]. Journal of Engineering for Industry, 1975, 97(2): 595-602.

[8] 常宗瑜, 张策, 王玉新. 含间隙机械系统动力学响应的特征[J]. 机械科学与技术, 2000, 19(3): 353-358.

[9] CHANG Zong-yu, LI Hua-jun. Dynamic response of deep groove ball bearing with point defects[J]. MMT, 2002, 12(2): 101-125.

[10] 张策. 机械动力学[M]. 北京: 高等教育出版社, 2008: 224-265.

Dynamicanalysisofhighspeedcammechanismwithclearancebasedonimpactmodel

In order to improve the dynamic performance of cam mechanism with high clearance. The two-state impact sub-model is used to simulate the gap between the cam and the follower to construct the dynamic model of the gripping cam mechanism considering the damping. The finite difference method is used to solve the dynamic equation with the cycloidal cam curve as the excitation function. The time domain and frequency domain analysis of the gap dynamics model are carried out, and the corresponding acceleration time domain and frequency domain response map are drawn. The influence of the damping ratio and the cycle ratio on the dynamic response is obtained. Then, several high speed cam curves are kinetics analysis. It is concluded that the existence of the gap will lead to the deterioration of the response accuracy of the system. The effect of the gap on the accelerating section of the follower is small, which has a great influence on the deceleration and deceleration period. The application of traditional theory in gap dynamics is limited.

high speed cam mechanism with clearance; dynamic model; time domain analysis; frequency domain analysis

何雪明(1966—)，男，江南大学教授，博士。

E-mail：hxuem2003@163.com

2017—06—01

10.13652/j.issn.1003-5788.2017.09.018