易感者宿主的移动对宿主-寄生虫相互作用的影响*

2017-11-16张芬芬张菊平

重庆工商大学学报（自然科学版） 2017年6期

关键词：感者平衡点寄生虫

张芬芬，张菊平

(1.中北大学朔州校区，山西朔州 036000；2.中北大学理学院，太原 030051)

易感者宿主的移动对宿主-寄生虫相互作用的影响*

张芬芬1，张菊平2

(1.中北大学朔州校区，山西朔州 036000；2.中北大学理学院，太原 030051)

建立对逼近模型来研究易感者宿主的移动对宿主-寄生虫相互作用的影响，采用理论分析得到无病平衡点和地方病平衡点，并利用Routh-Hurwits判据研究无病平衡点的渐近稳定性，得到了形成地方病的临界值；进一步用Matlab 给出了相应的计算机模拟；结论发现了一些重要现象，丰富了传染病的数学理论。

宿主-寄生虫；对逼近；易感者宿主的移动

传染病是由各种病原体引起的能在人与人、动物与动物或人与动物之间相互传播的一类疾病。历史上传染病的每一次爆发，都给人类造成了重大灾难。因此，建立传染病动力学模型，并以此来研究传染病的传播机理，为制定防治决策提供理论依据显得尤为重要[1]。传统的动力学平均域模型总是假设种群在空间中的传播是同质的，即假设空间中的所有个体以相同的概率与其他每一个个体进行接触。然而，在大多数情况下种群在空间中的位置会对他们的动力学行为(如出生、死亡)产生重大影响，尤其是那些直接传播的疾病，传播行为是局部的，更容易发生在直接相邻的两个个体之间。因此空间结构是种群的动力演化系统的一个重要组成部分。

成对近似的方法能很好地反映种群动力学中的空间结构,在过去的几十年里得到了很大的发展，建立了很多宿主-寄生虫的模型[2-3],流行病模型[4-5]等。本文正是想借助成对近似的方法来研究易感者宿主-寄生虫相互作用。为了处理上的方便，在以前研究的过程中很少考虑宿主的空间位置变化，而在实际生活中宿主在小范围内移动也是经常发生的事情，这也是本文研究的重点所在。

1 模型

考虑基本的SIS模型，其中S是没有感染寄生虫的宿主称为易感者，I是感染了寄生虫的宿主称为染病者，且进一步考虑一个规则网格上的点，其中每一个点的状态属于集合：A={O,S,I}，其中O表示网格上的点不被占据，S表示被一个易感者个体占据，I表示被一个染病者个体占据。用Pi(t)表示在时刻t，随机选择一个点的状态为i的概率，Pij(t)表示在时刻t随机选择一对最近邻居的状态为ij的概率。qj/i(t)为条件概率，表示在时刻t随机地取一个点的状态为i的条件下，一个最近邻居状态为j的概率。qk/ij(t)表示时刻t随机选择一个点的状态为i，在它已经有一个状态为j的最近邻居的情况下，另一个最近邻居的状态为k的概率，其中i,j,k∈A。单点的方程如下：

(1)

(2)

(3)

b表示出生率，d表示死亡率,α表示疾病所导致的死亡率,β表示感染率。这里考虑只有易感者能产生后代，且出生是局部的，即一个易感者只能向它周围最近邻居的空点产生后代。而且感染也是局部的，即只能通过染病者与它的最近邻居的易感者之间的直接接触而发生。进一步，考虑易感者宿主只能向最近邻居的空点移动，留下原来的点为空。并且不考虑外来物种的移入，也没有内部种群向外迁移。用l表示易感者的移动率，Y表示最近邻居的数目(考虑Von Neumann邻居,格子为周期边界条件,即每一个点都有4个最近邻居,且η=1/Y=0.25,表示一个最近邻居在所有的最近邻居中所占的比例)。成对近似模型如下：

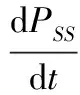
(4)

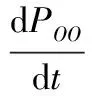
(5)

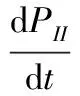
(6)

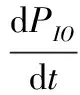
(7)

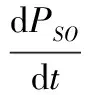
(8)

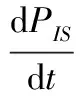
(9)

式(4)中的右边第1项表示易感者的自然死亡所导致的SS对密度的减少(即SS→SO或SS→OS)。第2项表示易感者被染病者所感染而导致SS对密度的减少，其中染病者位置位于易感者的其他Y-1最近邻居中的一个，在这个易感者已经有1个易感者最近邻居的情况下。第3项表示SS对密度的增加即OS或SO→SS)，该过程发生或者由于OS或SO中S的出生，或者由于空格子的其他Y-1个邻居中S的出生。第4项表示SS对中，易感者向其他Y-1个最近邻居中的1个空格子移动时所导致的SS对密度的减少。第5项表示OS或SO中，中心空格子的其他Y-1个最近邻居中的S向中心空格子移动所导致的SS对的增加。第6项表示SI或IS中，染病者的恢复所导致的SS对的增加。其余式子中各项的含义和式(4)类似，又有如下公式：

Pij=Piqj/i=Pjqi/j=Pji

(10)

(11)

(12)

封闭式(1)—式(9)要运用普通成对逼近(OPA)[4,6]方法，即让qk/ij=qk/i。接下来就可以对系统进行平衡点分析了。

2 平衡点分析

2.1 寄生虫入侵的判别

计算寄生虫入侵宿主的临界感染率。令

则包括I的方程可以写成：

其中

这里

A=-(d+α+μ)-(b+l)(1-η)qS/O

B=d+(β+l)(1-η)qO/S

C=-(2d+α+μ)+β(1-η)qS/S-β(η+(1-η)qI/S)-l(1-η)qO/S

D=2β(η+(1-η)qI/S)

现考虑无病平衡点，令PI=PII=PIO=PIS=0，所有包含I的条件概率也都为0。令式(1)—式(9)左边导数为零，则由式(2)有：

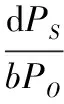
由式(5)可得：

d-b(1-η)qO/O-l(1-η)qO/O+

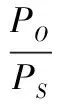
(13)

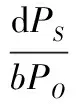
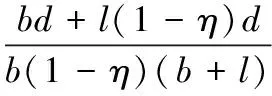
从而

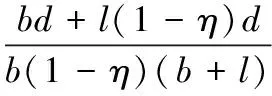
由式(1)可得

(1)模拟招聘比赛。该比赛主要依托我校的跨专业综合实验区，如图1所示。该实验区由对抗区、公共服务区、外贸区、采购区、自主学习区、路演区等部分组成，能够很好的满足模拟招聘比赛的需要。比赛经历简历初选、模拟面试、企业嘉宾面试共三个环节。具体的，参赛人员准备个人简历上交，根据简历筛选出50名参赛人员；参赛人员抽签随机分为5组；分组完成后，每一组内进行抽签，决定面试官与应聘者角色(两个面试官，八个面试人员)；进行模拟招聘时，评委进行观摩并分别为面试双方打分；最后，由企业嘉宾担任面试官，进行面试活动，学生观摩。

进而可得

PS=1-PO=

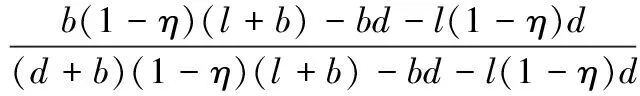
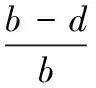
把计算出的平衡点的值代入矩阵M，计算行列式λE-M的值，得到

λE-M=(λ+d+α+μ)H(λ)

其中H(λ)=λ3+C2λ2+C1λ+C0。显然特征方程λE-M=0，已经有1个负的特征根：

λ=-(d+α+μ)

进而，只需要判断H(λ)的特征根的符号就可以判定无病平衡点的稳定性情况。

由Hurwtiz判据可知[7-9]，当满足以下条件时，根是稳定的

C2>0，C2C1-C0>0，C0>0

(14)

当C0>0成立时，式(14)中的前两项自然成立。故C0=0为一个临界值，并由此可解得：

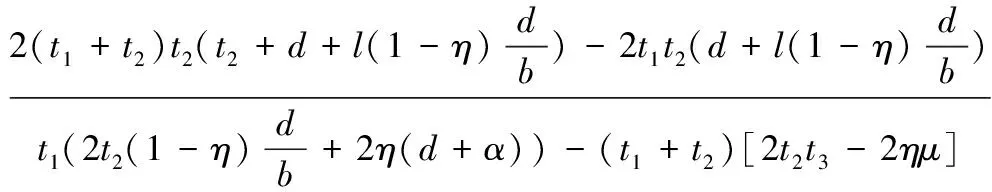
其中：

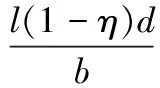
t2=d+α+μ

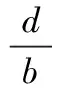
如果β>βC，则无病平衡点是不稳定的，将会形成地方病。如果β<βC，不会形成地方病。

2.2 地方病平衡点分析

令式(1)—式(9)左边导数为零，则由式(3)和式(10)可以得到：

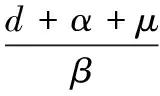
则由式(10)可得：

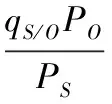
由式(6)有：

从而可以得到

qO/I=1-qS/I-qI/I=1-η-

qS/S=1-qO/S-qI/S=

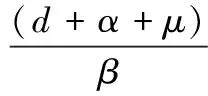
最后，由式(4)和式(7)可得：

-(d+α+μ)qO/I+dqS/I+(d+α)qI/I+β(1-η)qS/IqO/S- (b-l)(1-η)qS/OqO/I+l(1-η)qO/SqS/I=0

将上面推导得到的平衡点的值代入，就可以得到关于PS和PI的两个非线性方程。进而可以用数值解给出其在平衡点处的概率和条件概率。

3 结论

分别取参数b=2,d=1,η=0.25,μ=0.5,α=0.3。图1和图2给出了形成地方病所需要的临界感染率βC和易感者宿主种群的移动率l之间的关系。图3给出了l=0，l=10，l=50时无病区域和地方病区域的变化趋势。图4给出了βC和出生率、移动率之间的关系。由图1,图2可以看出随着移动率的增大，临界感染率在减小，但是当移动率增大到一定程度时，感染率变化不太明显，达到一个稳定值。也就是说易感者宿主的移动使得疾病比较容易传播，但由于易感者宿主接触的个体是有限的，于是临界感染率不会随着易感者宿主移动率的增大无限减小，而是达到一个饱和水平。

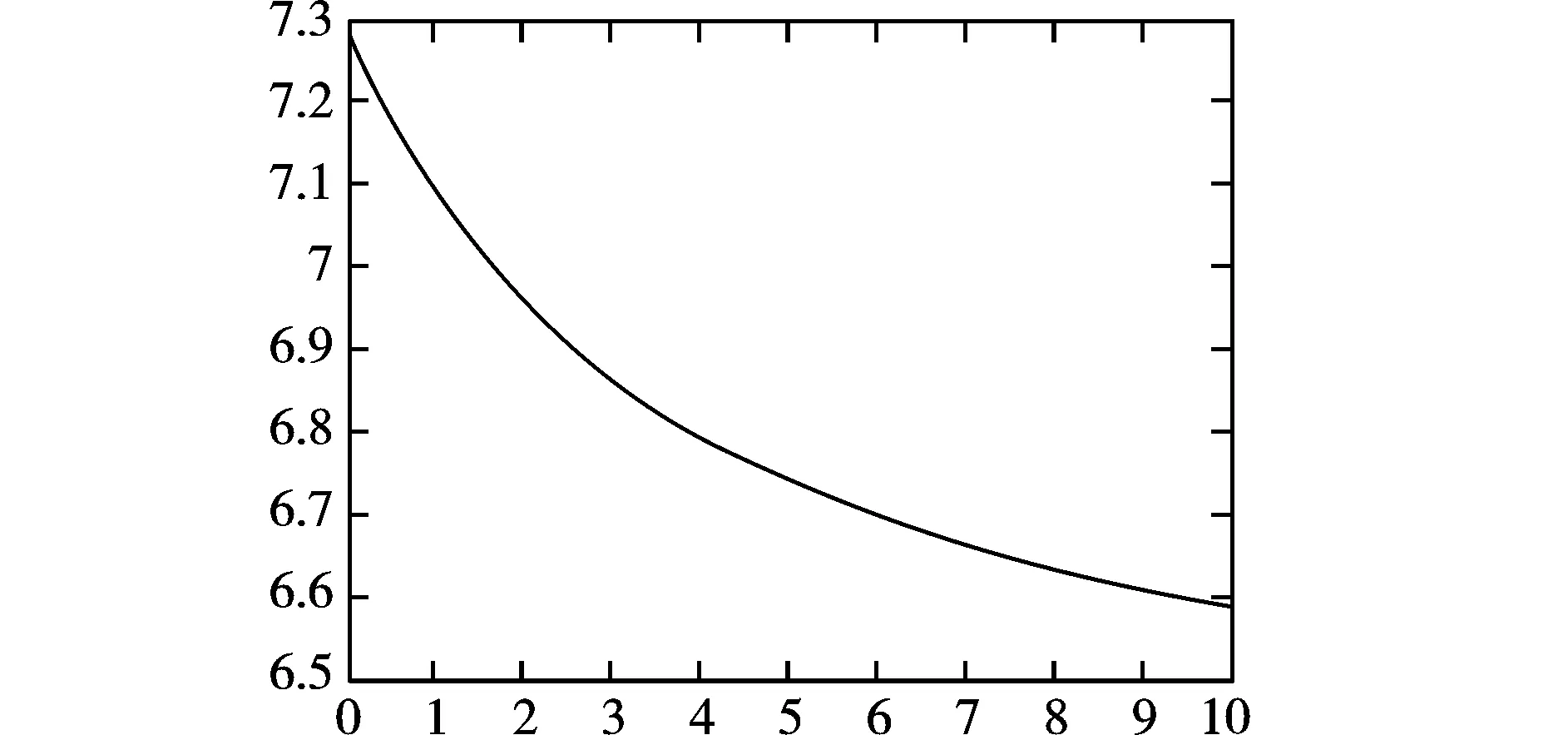
图1 临界感染率随着移动率的演化图(0≤l≤10)Fig.1 The diagram of critical infection rate changing with mobility(0≤l≤10)

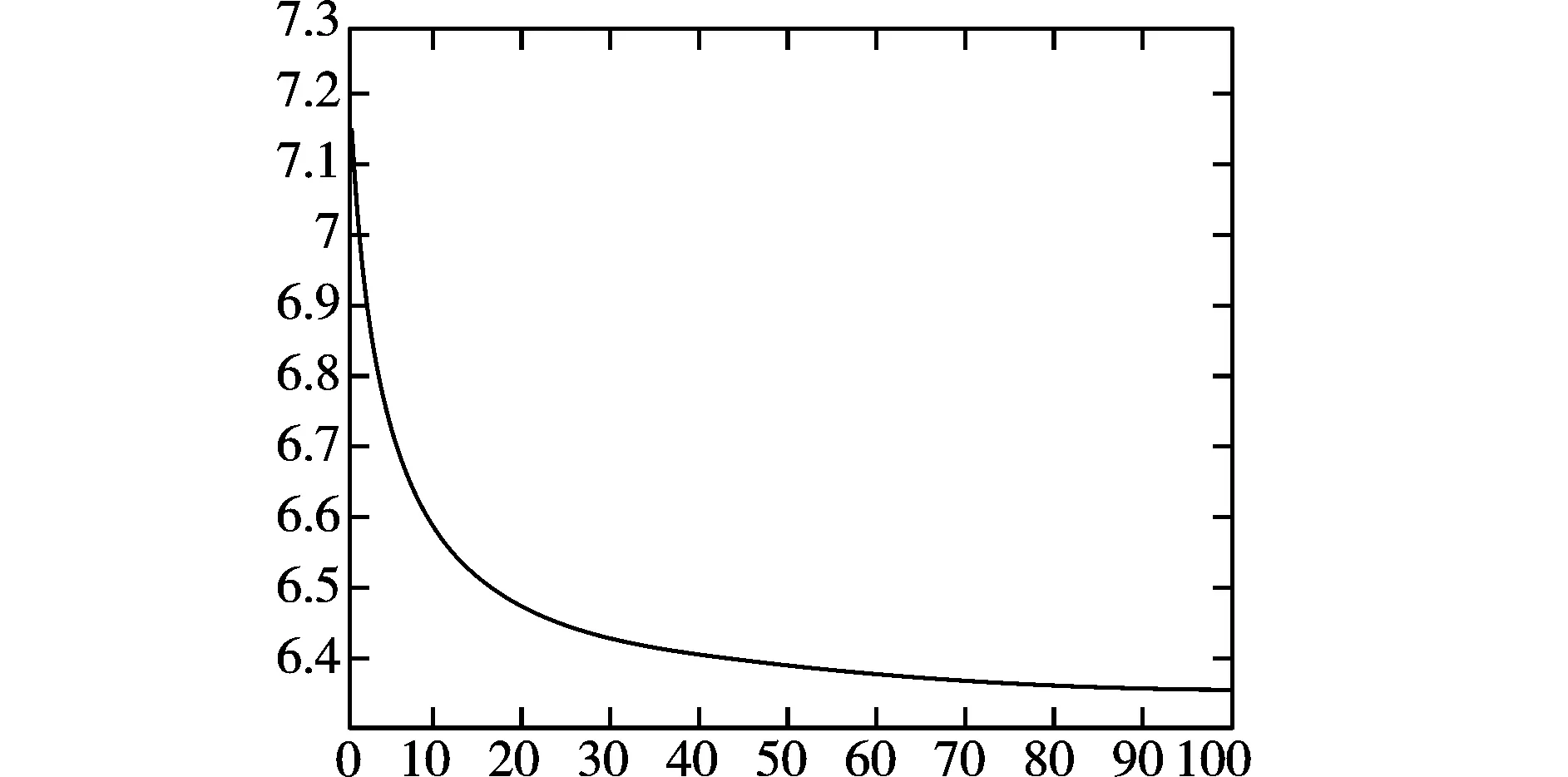
图2 临界感染率随着移动率的演化图(0≤l≤100)Fig.2 The diagram of critical infection rate changing with mobility(0≤l≤100)

图3 无病区域和地方病区域的变化趋势图Fig.3 Changing trend diagram of disease-free areas and endemic areas

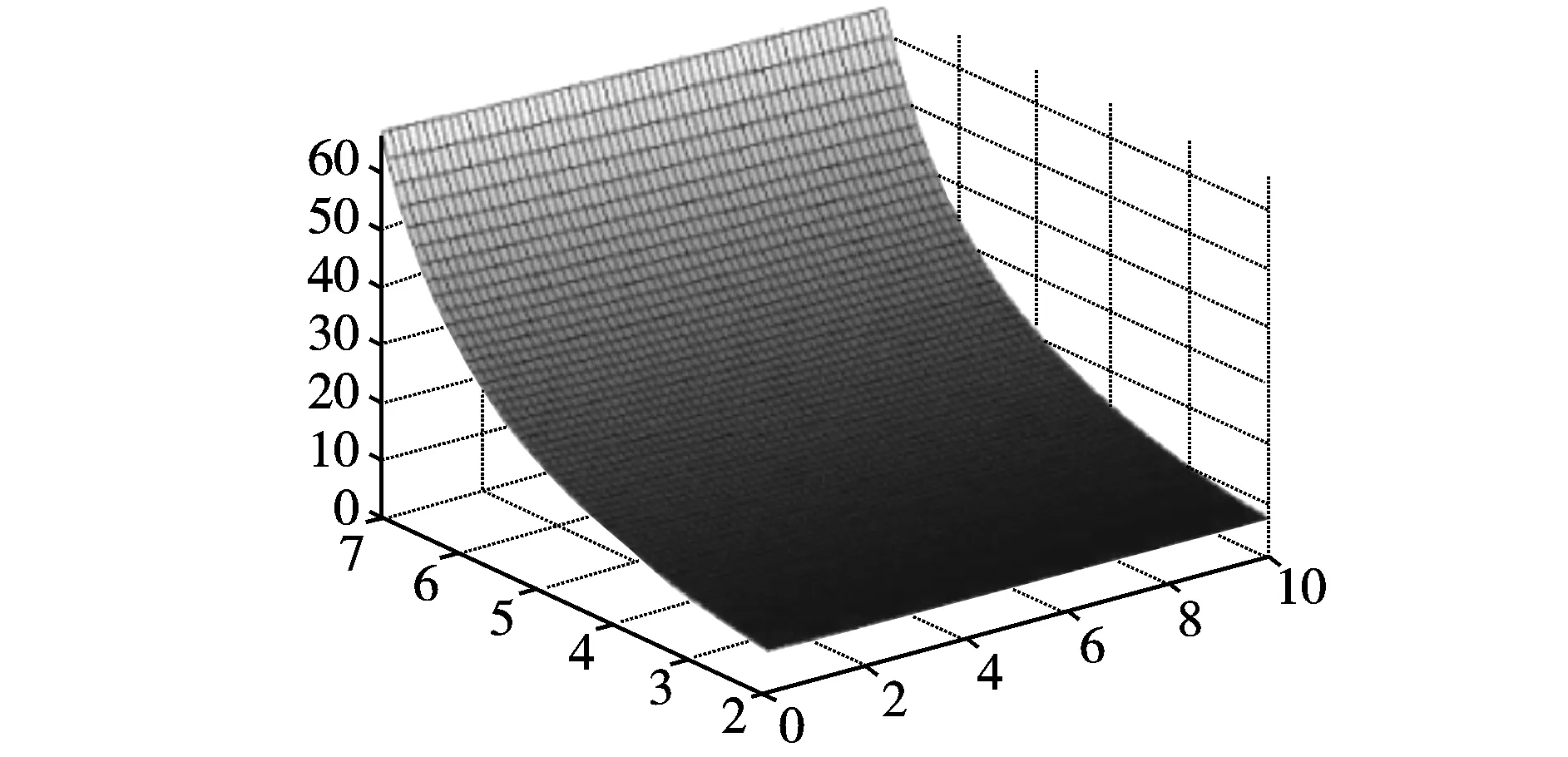
图4 临界感染率随着移动率和出生率的演化图Fig.4 The diagram of critical infection rate changing with mobility and birth rate

建立了宿主-寄生虫相互作用对逼近模型，研究了易感者的移动对寄生虫的入侵的影响。采用理论分析得到无病平衡点和地方病平衡点，并利用Routh-Hurwits判据研究无病平衡点的渐近稳定性，得到了形成地方病的临界值。进一步用Matlab给出了相应的计算机模拟。发现了一些重要现象，丰富了传染病动力学的数学理论。然而，对于内部种群向外迁移、外部移民的情形，由于处理起来比较复杂，研究很少。但同时，这又是自然界中常见的现象，也是进一步研究的重点。希望本文的工作能对今后的研究起到一定的帮助作用。

[1] 靳祯，孙贵全，刘茂省.网络传染病动力学建模与分析[M].北京:科学出版社，2016

JIN Z, SUN G Q, LIU M X. Modeling and Analysis of Infectious Diseases Dynamics of Network[M]. Beijing:Science Press, 2016

[2] STEVEN D W, MATT J K, MIKE B.The Role of Spatial Population Structure on the Evolution of Parasites with Acquired Immunity and Demograthy[J]. Journal of Theoretical Biology, 2013(324):21-31

[3] STEVEN D W, MATT J K, MIKE B. A Theoretical Study of the Role of Spatial Population Structure in the Evolution of Parasites Virulence[J]. Theoretical Population Biology, 2013(84):36-45

[4] RINGA N, BAUCH C T. Dynamics and Control of Foot-and-mouth Disease in Endemic Countries: A Pair Approximation Mode[J]. Journal of Theoretical Biology, 2014, 357(21):150-159

[5] PETERMANN T, DELOSRIOS P. Cluster Approximations for Epidemic Processes: A Systematic Description of Correlations Beyond the Pair Level[J]. Journal of Theoretical Biology, 2004, 229(1):1-11

[6] MAKOTO K, NORIO K. Upper Bounds for Survival Probability of the Contact Process[J]. Journal of Statistical Physics, 1991, 63(1):115-130

[7] 马知恩, 周义仓. 常微分方程定性与稳定性方法[M]. 北京:科学出版社,2001

MA Z En, ZHOU Y C. Qualitative and Stability Method of Ordinary Differential Equation[M]. Beijing: Science Press, 2001

[8] 童姗姗,仝云旭. 具时滞阶段结构和非线性发生率的SIS模型[J]. 重庆工商大学学报( 自然科学版), 2016, 33(2): 1-4

TONG S S, TONG Y X. SIS Epidemic Model with Time Delay，Stage-structrue and Nonlinear Incidence[J].Journal of Chongqing Technology and Business University (Natural Sciences Edition), 2016, 33( 2): 1-4

[9] 杨文川. 基于斑块环境下SIS传染病模型局部稳定性分析[J]. 重庆工商大学学报( 自然科学版), 2015, 32(3): 21-24

YANG W C. Local Stalility Analysis Based on an SIS Epidemic Modeling in Patches Environment[J]. Journal of Chongqing Technology and Business University (Natural Sciences Edition), 2015, 32(3): 21-24

The Influence of Host-parasite Interactions on the Role of Susceptible Host’s Movement

ZHANGFen-fen1，ZHANGJu-ping2

(1.Shuozhou College, North University of China, Shanxi Shuozhou 036000, China; 2.Department of Mathematics, North University of China, Shanxi Taiyuan 030051, China)

A pair approximation model is established to study the effect of the susceptible host’s movement on host-parasite interactions. Disease-free equilibrium and endemic equilibrium are obtained by theoretical analysis. Through the discussion of local asymptotic stability of disease-free equilibrium by the Routh-Hurwits, the critical value is obtained so that the infection is established. In addition, the corresponding computer simulation is given by Matlab. The conclusion has found some important phenomena and enriched the mathematical theory of infectious diseases.

host-parasite ; pair approximation; the susceptible host’s movement

O701