新型双臂菱形压电柔性机构理论设计与建模
2017-11-15曹军义凌明祥曾明华
蒋 州 曹军义 凌明祥,2 曾明华 林 京
1.西安交通大学机械工程学院,西安,7100492.中国工程物理研究院总体工程研究所,绵阳,621900
新型双臂菱形压电柔性机构理论设计与建模
蒋 州1曹军义1凌明祥1,2曾明华1林 京1
1.西安交通大学机械工程学院,西安,7100492.中国工程物理研究院总体工程研究所,绵阳,621900
针对目前传统菱形位移放大机构的输出刚度、固有频率和位移放大比无法同时提高的问题,提出了一种双臂复合菱形柔性机构,并介绍了其理论设计与建模方法。基于欧拉-伯努利梁理论和卡氏第二定理,推导出双臂复合菱形柔性机构的位移放大比和刚度解析模型,利用拉格朗日方程建立了该柔性机构的固有频率解析模型,并通过商业有限元软件验证了解析模型的准确性。根据理论计算结果,通过电火花切割工艺加工出复合柔性机构,并与相同尺寸参数的传统菱形位移放大机构进行实验比较研究。实验结果表明,压电双层臂柔性机构的固有频率为1330 Hz,位移放大比为4.2,同时提高了固有频率和放大比。此外,所建立的位移放大比和固有频率力学解析模型可以为新型压电柔性机构的优化设计提供理论指导。
压电执行器;微位移放大;柔性铰链;三角形位移放大机构
0 引言
近年来,随着微电子[1]、光学微装配以及超精密加工[2]等领域的迅猛发展,人们对精密定位技术提出了越来越高的要求。压电陶瓷具有分辨率高、驱动力大、响应速度快等优点,成为精密定位平台中使用最广泛的驱动器件[3]。此外,压电陶瓷在振动主动控制、精密阀、精密泵等领域也得到了广泛的关注和应用[4]。但是,压电陶瓷最大的不足是输出位移小,正常工作状态下输出位移仅是其自身尺寸的0.1%~0.2%。为实现亚毫米级的微位移输出,工程实践中常采用柔性位移放大机构来满足实际需求[5]。
微位移放大机构的常用放大原理有杠杆放大、压曲放大、液压放大、三角形放大等[6]。张建瓴等[7]基于差式杠杆原理设计了微位移放大机构,并对该机构放大倍数和静态刚度进行理论建模。杠杆放大机构的缺点是尺寸较大,输出刚度和固有频率较低。压曲放大机构利用薄板或较薄壳体受外力而产生的弯曲变形来进行位移放大,放大倍数与薄板的曲率以及薄板间的夹角有关,放大倍数较小[8]。液压放大机构利用液体等体积原理,通过驱动活塞运动实现位移放大,主要应用于精密伺服阀[9]。三角形放大机构利用三角形三边之间的几何关系,通过改变长直角边的位移来实现短直角边位移的放大。在众多位移放大机构中,三角形位移放大机构因其放大倍数大、结构紧凑、固有频率高、位移输入输出之间具有良好的线性关系等优点,在科学研究和工程实际中得到广泛应用。
三角形位移放大机构以菱形[3]、桥式(bridge-type)[10]、Moonie型[11]、Cymbal型[12]等为代表。目前,传统的菱形位移放大机构的输出刚度、固有频率和位移放大比三者之间无法同时达到最优,设计时一般是在这些指标中进行折中处理。为此,本文提出了一种双层菱形柔性机构,其特点是结构紧凑,在保持位移放大比的同时提高了机构的输出刚度和固有频率,并采用卡氏第二定理和拉格朗日方程进行静力学和动力学解析建模和理论分析,最后加工出实验样机,并进行实验验证。
1 新型双臂菱形压电柔性机构
传统的菱形位移放大机构由于结构紧凑,位移放大倍数高,抗干扰能力强等优点得到了工程界的认可。但受限于菱形机构放大比与固有频率无法同时提高的缺陷,目前菱形放大机构主要应用于输出刚度较小、频响较低的工况。本文提出了一种具有双臂的复合菱形位移放大机构,在保持较大位移放大比的同时,可以提高系统输出刚度和固有频率,其具体结构如图1所示。

(a)双臂菱形柔性机构实物图
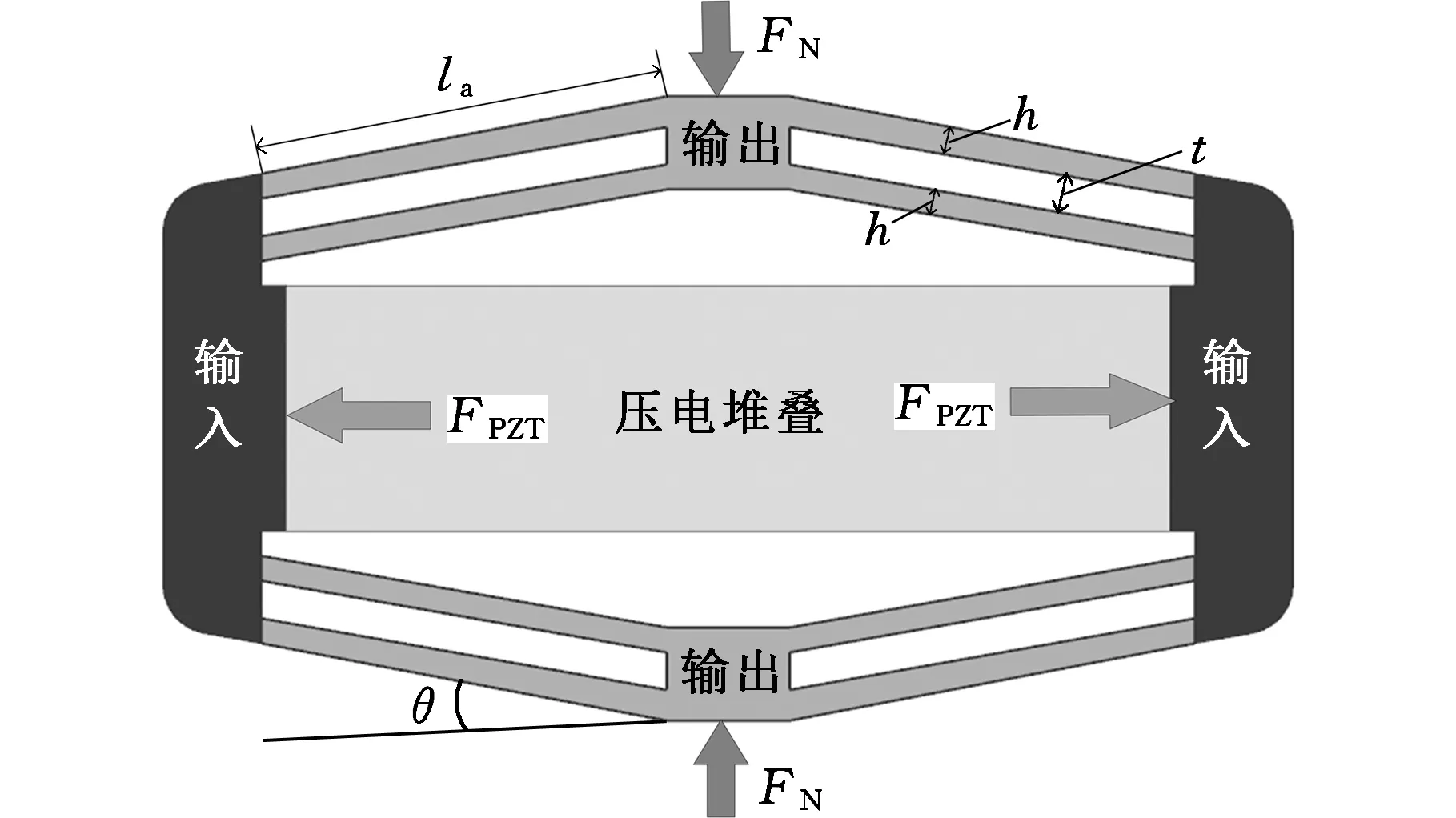
(b)双臂菱形柔性机构原理图图1 双臂菱形柔性机构Fig.1 Rhombus-type compliant mechanism with double flexible beams
整个机构与传统的菱形放大机构构型相似,上下、左右对称布局,但是放大机构的柔性臂采用双层结构。压电陶瓷通过一定预紧力安装在位移放大机构水平对角线之间,在一定的输入电压下,压电陶瓷输出驱动力和水平位移,在其驱动作用下,菱形双臂发生形变而使位移放大机构产生竖直方向的输出位移。合理优化机构参数,可得到被放大的竖直方向位移输出。机构运动过程中保持菱形构型不变,与传统同参数的菱形放大机构相比,双臂菱形放大机构在运动过程中几何关系不变,大角度位移放大比几乎不变;由单臂变为双臂结构,提高了机构的输出刚度和固有频率。
2 新型柔性机构的解析模型
2.1位移放大比模型
如图2所示,假设压电陶瓷输出力和负载分别为FPZT和FN,其他几何参数定义见图1。当压电陶瓷在正电压作用下,位移放大机构水平方向伸长2Δx时,其竖直方向将缩减2Δy。由于机构具有对称性,取柔性位移放大机构的1/4进行力学分析,则有如下关系式成立:FPZT=4fx;FN=4fy。如图2所示,柔性双臂机构由柔性臂AB和柔性臂CD组成,因柔性臂AB与柔性臂CD的力学边界条件以及几何参数完全相同,为简化力学分析过程,以柔性臂AB为例,对双臂菱形位移放大机构进行受力分析。考虑柔性臂的固定边界条件:A、B两点转动角度相等,A点作水平移动,B点作竖直运动。由于受到A、B两点的约束,柔性臂AB将受到2Mr力矩的作用,根据力平衡方程和力矩平衡方程,有
fAx=fBx=fx=FPZT/4
(1)
fAy=fBy=fy=FN/4
(2)
2Mr=fxlasinθ+fylacosθ
(3)
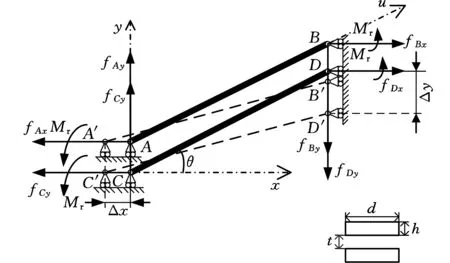
图2 双臂菱形机构受力分析Fig.2 Force analysis of rhombus-type displacement amplifier
对简化后的柔性臂AB进行受力分析。沿柔性臂方向,AB受到拉力的作用;垂直于柔性臂方向,AB受到一对力偶的作用,且A、B两点的约束还导致AB存在力矩2Mr的作用,这将使柔性臂在运动过程中发生弯曲,进而输出放大的位移。根据力和力矩平衡方程,沿AB长度方向、距A点距离为u的力和力矩分别为
(4)
基于欧拉-伯努利梁理论,柔性臂的总变形能为拉伸应变能Vε1与弯曲应变能Vε2之和,即
Vε=Vε1+Vε2
(5)
由卡氏第二定理,机构沿x方向的位移

(6)
机构沿y方向的位移

(7)
其中,EA和EI分别为柔性臂AB的抗拉刚度和抗弯刚度。基于式(6)和式(7),位移放大机构空载时(fy=0)的位移放大比

(8)
位移放大机构的输入刚度

(9)
2.2固有频率解析模型
与实际应用工况一致,建立固有频率解析模型时,位移放大机构的底部边界条件是固定的,各柔性环节的质量和坐标选取如图3所示。
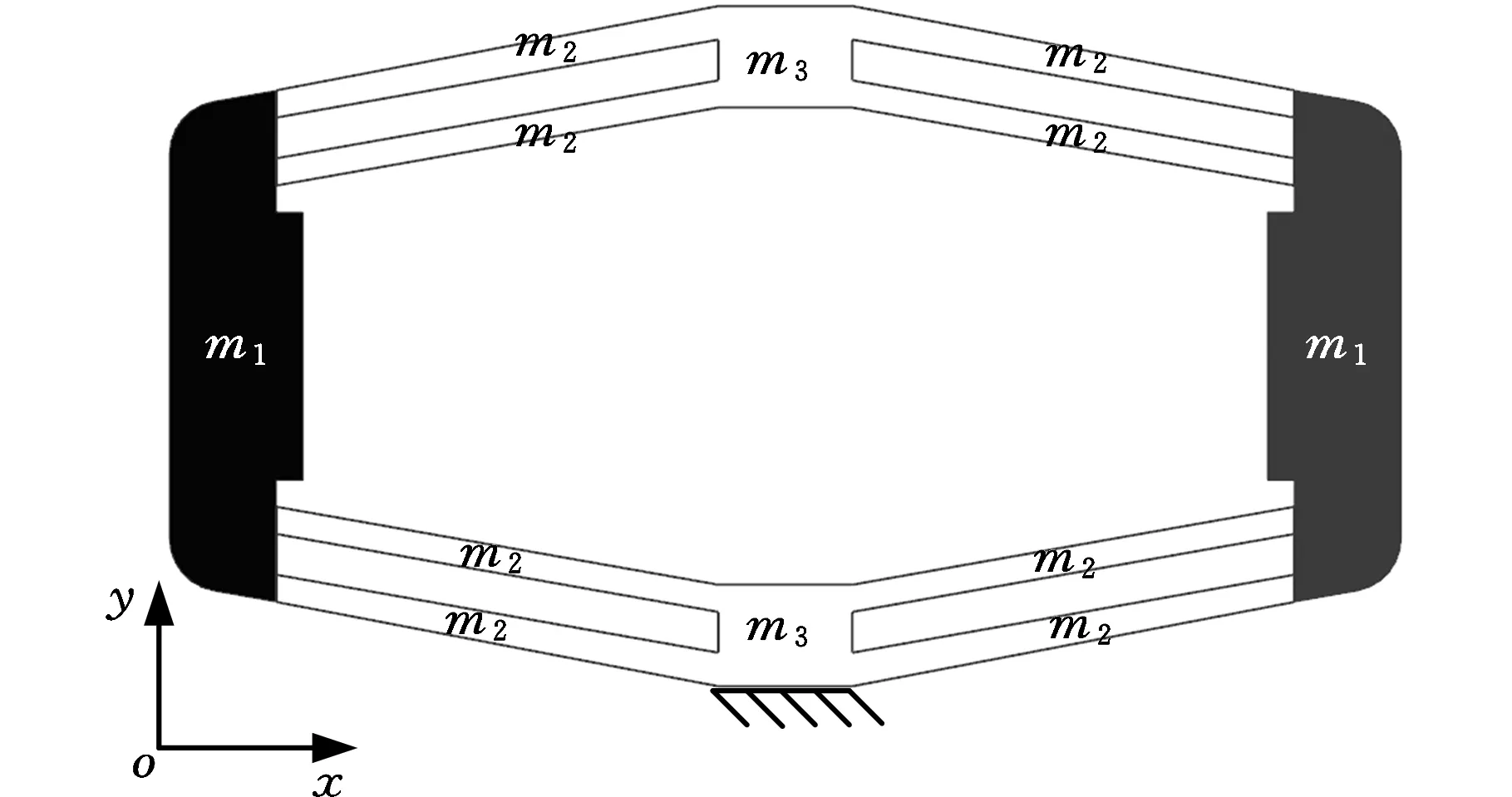
图3 双臂菱形位移放大机构及各部分质量分布Fig.3 Mass distribution of the proposed mechanism
仅考虑柔性位移放大机构竖直方向的输出位移一个自由度,取广义坐标q=2Δy。由前文力学分析和理论建模结果可知,水平输入位移Δx、柔性臂转动角度Δθ、柔性臂变形伸长量Δl与竖直输出位移坐标q之间分别满足如下关系:
(10)

(11)
式中,Kl、Kθ分别为柔性臂AB、CD的抗拉刚度和抗弯刚度。
考虑到柔性臂的抗拉刚度和抗弯刚度,则系统的弹性势能
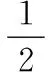
(12)
系统的动能
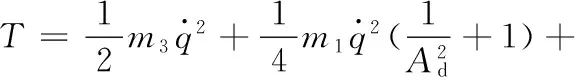
(13)
令拉格朗日函数L=T-V,对于自由振动,将式(12)和式(13)代入拉格朗日方程:

(14)
忽略推导过程,根据拉格朗日方程,可以得到自由振动的动力学方程:
(15)
双臂菱形柔性机构的固有频率

(16)
3 有限元计算分析
3.1位移放大比仿真
为了验证本文力学解析模型的准确性,保持双臂菱形位移放大机构的参数相同,将解析模型计算结果与有限元计算结果进行比较,并将有限元计算结果作为比较的基准。位移放大机构具体几何参数见表1,有限元计算的网格划分如图4所示。
进行位移放大比仿真计算时,完整约束图4模型底部,柔性机构水平对角线内部两侧施加等大反向的驱动力;计算位移放大比仿真结果时,柔性机构的位移放大比即仿真结果的竖直输出位移与水平输入位移的比值。计算得到的双臂菱形位移放大比的部分结果见表2。

图4 有限元模型Fig.4 Finite element model

参量数值参量数值la(mm)16.8d(mm)10h(mm)1.0E(GPa)210t(mm)1.5ρ(kg/m3)7850

表2 位移放大比计算结果
由表2可以看出,本文基于卡氏第二定理推导出的解析模型在角度θ较大时与有限元结果接近,在角度θ较小时还存在一定的误差。存在计算误差的主要原因是本文的双层柔性臂是中空结构,在计算其弯矩时未考虑中空部分的影响。实际工程应用中应乘以工程系数进行调整,这样,解析模型计算结果将与有限元计算结果更加接近。
3.2固有频率仿真
工作频宽和输出位移放大倍数是评价位移放大机构性能的两个重要参数,建立固有频率与机构几何参数之间准确的解析力学模型是结构优化的前提。为了验证本文建立的双臂菱形位移放大机构固有频率解析模型的准确性,基于ANASYS软件对同一模型进行了有限元模态分析,有限元计算的网格划分如图4所示,具体结构参数见表1,其中,柔性机构的角度θ为10°。
双臂菱形位移放大机构的前6阶模态如图5所示,其中,第1阶模态描述了双臂菱形位移放大机构的平面外摇摆变形,频率约1179 Hz;第2阶模态为机构绕Z轴扭转变形,频率约1257 Hz;第4阶模态为机构绕上下定点的扭转变形,频率约3806 Hz;第3阶模态为位移放大机构输出位移方向的变形振型,频率为1411.4 Hz,理论计算出该阶固有频率为1292.91 Hz,两者的相对误差为9.2%,误差在工程许可范围内。

图5 菱形位移放大机构的前6阶振型Fig.5 The first six vibration modes of the proposed mechanism
4 实验验证
按表1中的参数加工出双臂菱形柔性机构和传统菱形柔性机构,其中,柔性机构的角度θ为10°。双臂菱形柔性机构在传统菱形柔性机构的基础上改进,除增加双臂结构外,其他尺寸参数与传统菱形机构相同。搭建实验测试系统进行比较与验证(图6)。实验中,由信号发生器(AFG 300)产生激励信号,经功率放大器放大后输入压电陶瓷,在压电陶瓷激励下,柔性机构输出微位移,该微位移由激光位移传感器进行测量,位移传感器所测位移和功率放大器输出信号由示波器(Agilent,探头内阻为10 MΩ)进行同步采集。压电陶瓷功率放大器型号为PI-E-482,电压放大倍数为100;所用传感器型号为HL-G103-A,分辨力为0.5 μm。

图6 实验测试系统Fig.6 Experimental set up
对压电陶瓷施加正弦线性扫频激励,频率范围为1~2000 Hz,扫频时间100 s,输入电压幅值20 V。实际输入输出曲线如图7所示,可以看出在扫频激励67 s后,放大机构出现共振现象。

图7 扫频输入输出信号Fig.7 Input and output sweep-frequency signal
放大机构竖直方向的位移输出由激光位移传感器测得,分析放大机构的输入输出得到系统的伯德图(图8)。实测双臂菱形位移放大机构固有频率为1330 Hz,由有限元仿真分析对应该阶固有频率为1411.4 Hz,误差为5.77%,仿真与实验误差较小,表明仿真模型比较准确,可信度比较高。由图8可以看出,本文提出的双臂菱形柔性机构与传统的菱形机构相比,固有频率有了一定的提高;双臂菱形柔性机构的固有频率为1330 Hz,传统菱形机构固有频率为1140 Hz,机构固有频率提高了16.7%,输出刚度增大了一倍,而位移放大比几乎不变,充分表明了本文所设计机构的优点。

图8 位移放大机构扫频分析伯德图Fig.8 Bode diagram of different amplification mechanisms
5 结语
实验测试结果表明,该双臂菱形柔性机构的固有频率比传统机构提高16.7%,输出刚度增大一倍,位移放大比为4.2,与传统机构接近。此外,基于本文建模方法所建立的位移放大比和固有频率等力学解析模型可以准确预测位移放大机构的静动力学响应,揭示双臂菱形柔性位移放大机构各几何参数对机构静、动力学行为的影响,可为机构优化设计和控制设计提供较为准确的依据。
[1] LING Mingxiang, CAO Junyi, JIANG Zhou, et al. Theoretical Modeling of Attenuated Displacement Amplification for Multistage Compliant Mechanism and Its Application [J]. Sensors and Actuators A: Physical,2016,15(22):15-22.
[2] 黄卫清,史小庆,王寅,等. 菱形压电微位移放大机构的设计[J].光学精密工程,2015,23(3):803-809.
HUANG Weiqing, SHI Xiaoqing, WANG Yin, et al. Design of Diamond Piezoelectric Micro-displacement Amplification Mechanism [J]. Optics and Precision Engineering,2015,23(3):803-809 .
[3] 凌明祥,曹军义,曾明华,等. 压电柔性机构位移放大比精确建模[J].智能材料与结构,2016,25:075022.
LING Mingxiang, CAO Junyi, ZENG Minghua, et al. Enhanced Mathematical Modeling of the Displacement Amplification Ratio for Piezoelectric Compliant Mechanisms [J]. Smart Materials and Structures,2016,25:075022.
[4] 凌明祥,刘谦,曹军义,等.压电位移放大机构的力学解析模型及有限元分析[J].光学精密工程,2016,24(4):812-818.
LING Mingxiang, LIU Qian, CAO Junyi, et al.Analytical Model and Finite Element Analysis of Piezoelectric Displacement Amplification Mechanism[J]. Optics and Precision Engineering,2016,4(4):812-818 .
[5] 田延岭,张大卫,闫兵,等.二自由度微定位平台的研制[J].光学精密工程,2006,14(1):94-99.
TIAN Yanling, ZHANG Dawei, YAN Bing, et al. Development of a 2-DOF Micro-positioning Table [J]. Optics and Precision Engineering,2006,14(1):94-99.
[6] 林超,俞松松,程凯,等.微/纳米定位平台的动态特性分析与试验[J].浙江大学学报(工学版),2012,46(8):1375- 1381.
LIN Chao, YU Songsong, CHENG Kai, et al. Dynamic Analysis and Testing of Micro/nano-positioning Platform [J].Journal of Zhejiang University(Engineering Science),2012,46(8):1375-1381.
[7] 张建瓴,陈万银,可欣荣,等.一种微位移放大机构的设计与仿真[J].机械设计,2009,26(12):9-12.
ZHANG Jianling, CHEN Wanyin, KE Xinrong,et al.Design and Simulation of a Kind of Micro-displacement Amplification of a Kind of Micro-displacement Amplification Mechanism [J]. Journal of Machine Design,2009,26(12):9-12.
[8] 王兴松,王湘江,毛燕,等.基于超磁致伸缩材料的折弯型压曲放大机构设计、分析与控制[J].机械工程学报,2007,43(11):27-33.
WANG Xingsong, WANG Xiangjiang, MAO Yan, et al. Design, Analysis and Control of Novel Pressing and Bending Magnifying Mechanism Driven by Giant Magnetostrictive Material[J]. Chinese Journal of Mechanical Engineering,2007,43(11):27-33.
[9] 俞军涛,焦宗夏,吴帅.基于液压微位移放大结构的新型压电陶瓷直接驱动阀设计及仿真[J].机械工程学报,2013,49(2):151-158.
YU Juntao, JIAO Zongxia, WU Shuai. Design and Simulation Study on New Servo Valve Direct Driven by Piezoelectric Actuator Using Hydraulic Amplification[J]. Journal of Mechanical Engineering,2013,49(2):151-158.
[10] 马立,谢炜,刘波,等.柔性铰链微定位平台的设计[J].光学精密工程,2014,22(2):338-345.
MA Li, XIE Wei, LIU Bo, et al. Design of Micro-positioning Stage with Flexure Hinge[J]. Optics and Precision Engineering,2014,22(2):338-345.
[11] FREDERIC L, ZAFFIR C, CRAIG A R. A Simplified Geometrically Nonlinear Approach to the Analysis of the Moonie Actuator[J].IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control,1995,59(1):21-27.
[12] AYDIN D, KENJI U. Composite Piezoelectric Transducer with Truncated Conical Endcaps “Cymbal”[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control,1997,44(3):597-605.
TheoreticalDesignandModelingofaNovelPiezo-drivenRhombicFlexureMechanismwithDoubleBeams
JIANG Zhou1CAO Junyi1LING Mingxiang1,2ZENG Minghua1LIN Jing1
1.School of Mechanical Engineering,Xi’an Jiaotong University,Xi’an,710049 2.Institute of System Engineering,China Academy of Engineering Physics,Mianyang,Sichuan,621900
Design and modeling of a new diamond micro-displacement mechanism with double flexible beams was presented to overcome the issue that the output stiffness, natural frequency and displacement amplification ratio of the traditional diamond displacement amplification mechanism might not be improved at the same time. The static analysis model of displacement amplification ratio and input/output stiffness of the mechanism were derived based on Castigliano’s second theorem. Analytical model of natural frequency was also deduced by further employing the Lagrange equation .The finite element analysis was used to verify the accuracy of the analytical models. A prototype of the proposed compliant mechanism was machined by means of electric spark cutting processes and the performance measurement was performed for comparative analysis with the traditional mechanism with the same dimensions. Experimental results show that the natural frequency of the composite compliant mechanism is as 1330 Hz and displacement amplification ratio is as 4.2. In addition, the modeling method and the corresponding theoretical formula proposed herein may provide a useful reference for the optimal design and development of similar displacement amplification mechanisms.
piezoelectric actuator; displacement amplification; flexure hinge; triangle displacement amplification mechanism
TH113.2;TN384
10.3969/j.issn.1004-132X.2017.21.007
2016-12-05
国家自然科学基金资助项目(51575426,51421004)
(编辑陈勇)
蒋州,男,1993年生。西安交通大学机械工程学院硕士研究生。主要研究方向为压电智能结构建模与振动控制。E-mail:jiangzhou_xy@163.com。曹军义,男,1977年生。西安交通大学机械工程学院副教授、博士研究生导师。凌明祥,男,1986年生。西安交通大学机械工程学院博士研究生,中国工程物理研究院总体工程研究所工程师。曾明华,男,1993年生。西安交通大学机械工程学院硕士研究生。林京,男, 1971年生。西安交通大学机械工程学院教授、博士研究生导师。
