分数阶累加多变量灰色模型FMGM(1,n)及应用

罗佑新



分数阶累加多变量灰色模型FMGM(1,)及应用

罗佑新

(湖南文理学院洞庭湖生态经济区建设与发展省级协同创新中心，湖南常德，415000)

在分析单变量分数阶累加生成和累减生成的基础上，推导多变量分数阶累加生成的计算公式，建立多变量分数阶累加灰色模型FMGM(1,)，给出基于最小二乘法估计模型参数。以分数阶数为设计变量，以最小平均相对误差为目标函数，建立优化模型，以Matlab为平台编写优化求解程序。多变量分数阶累加灰色模型FMGM(1,)模型是单变量的FGM(1,1)模型在多变量情况下的自然推广，旨在反映各变量间相互制约、相互促进的关系。最后给出了算例，算例表明本文所建模型的适应性、有效性。

多变量分数阶累加灰色模型FMGM(1,)模型；优化；最小二乘法；模型参数估计

灰色系统理论立足于数据很少的灰系统，将已知数据序列进行数据变换处理，建立独具特色的微分方程模型，充分发掘较少数据中的显信息和隐信息，进而从无序的数据中发现有序，推知其未来的发展规律[1−3]。GM(1,1)模型是最常用的一种灰色系统模 型[2−3]，它通过单变量的一阶微分方程模型(属整数阶导数模型)揭示其内在发展规律,用于单一时间序列的建模和预测，而实际系统通常大都是分数阶的, 采用分数阶描述那些本身带有分数阶特性的对象时，能更好地揭示对象的本质特性及其行为，之所以忽略系统的实际阶次(分数阶)，主要是因其复杂性和缺乏相应的数学工具，这一“瓶颈”正被逐渐克服，相关成果不断涌现。分数阶微积分自1965年Leibniz提出后，在控制理论、图像处理等方面显示出强大的生命力和优越性[4]，它是将通常意义下的整数阶微积分推广到分数阶。对于灰色GM(1,1)模型，文献[5]提出了分数阶累加灰色模型GM(1,1)，文献[6]应用分数阶累加灰色模型GM(1,1)对武器维护费进行了预测，文献[7]对分数阶累加的离散灰色模型、文献[8]对分数阶累加灰色模型和分数阶累加的离散灰色模型进行了总结，并研究了分数阶灰色模型的适应范围。实际的社会、经济系统中往往包含多个变量。各变量相互关联、共同发展，这时，每一变量的发展变化都不是孤立的，1个变量要受到其他变量的影响，同时也影响着其他变量。文献[9]将单变量的GM(1,1)推广至个变量的多变量灰色模型MGM(1,)。灰色模型MGM (1,)不是GM(1,1)模型的简单组合，也不同于GM(1,)模型只建立单个元一阶微分方程，而是建立个元微分方程，通过联立求解，使MGM模型中的参数能够反映多个变量间相互影响、相互制约的关系。文献[10−12]对多变量灰色MGM模型加以改进，模型更加完备。灰色变量模型 GM(1,1)能扩展到多变量模型，整数阶单变量灰色模型GM(1,1)能扩到分数阶累加灰色模型FGM(1,1)。对于多变量整数阶灰色MGM如何扩展到多变量分数阶累加灰色模型FMGM(1,1)的问题，本文作者在分析单变量分数阶累加生成和累减生成的基础上，推导了多变量累加生成的计算公式，建立多变量分数阶累加灰色模型FMGM(1,)，给出基于最小二乘法估计模型参数,以分数阶数为设计变量，以最小平均相对误差为目标函数，建立优化模型。多变量分数阶累加灰色模型FMGM(1,)模型是单变量的FGM(1,1)模型在多变量情况下的自然推广，最后给出了算例，验证本文所建模型的适应性、有效性。

1 多变量分数阶灰色模型FMGM(1,n)

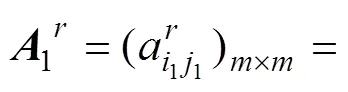
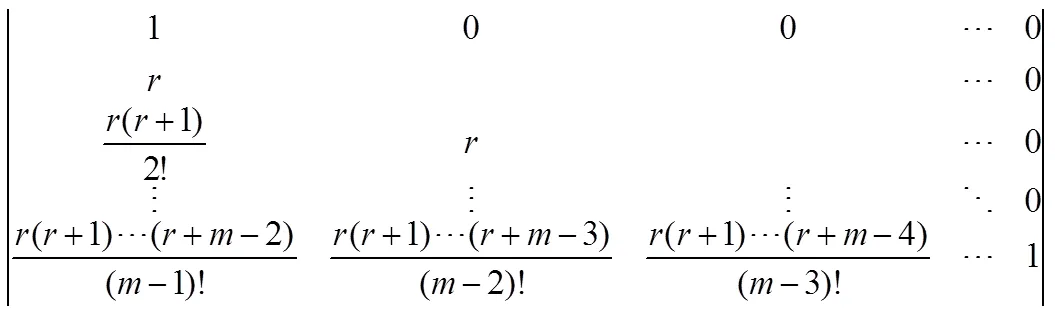
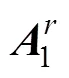
因而，

=1，2，…，(3)

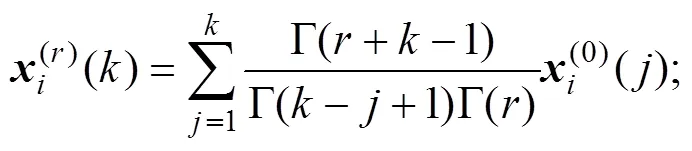
=1，2，…，(4)

FMGM(1,)模型为

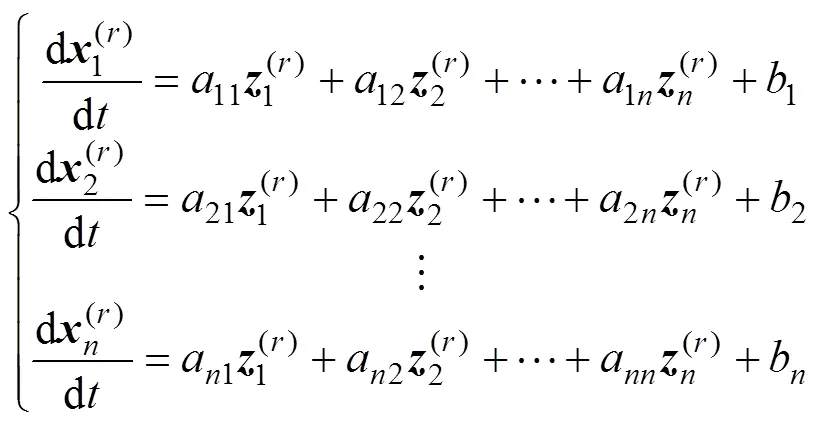
其白化微分方程为元阶微分方程组

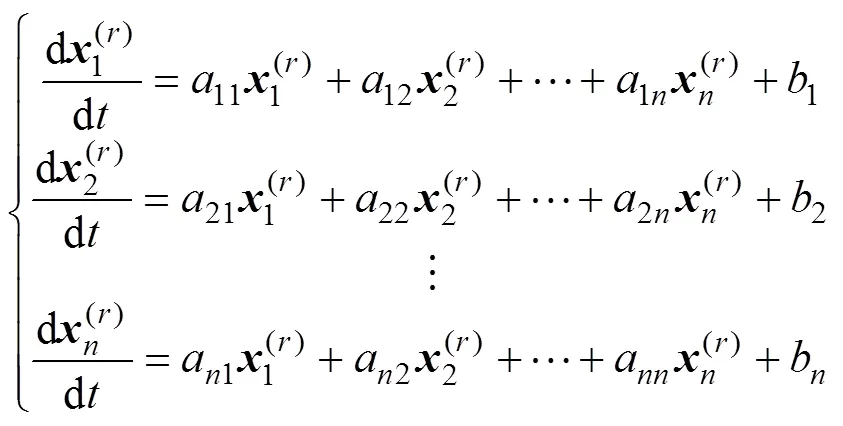
则式(5)可以表示为

为了辨别和，将式(5)离散得到

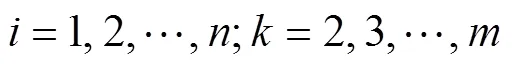
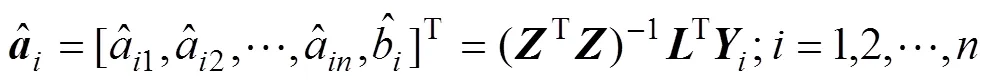
其中：

则可以得到和的辨别值：

FMGM(1,)模型的计算值为

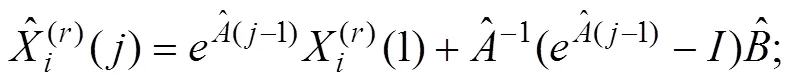
=1，2，…，(11)

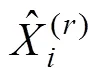
=1，2，…，(12)

定义第个变量的绝对误差为

第个变量的相对误差为

第个变量相对误差绝对值的平均值为

全体数据的平均误差为

上述模型为多变量分数阶累加灰色FMGM(1,)模型，当=1上述模型变为多变量灰色模型MGM(1,)。

给定分数阶数就可计算模型的解，为了得到最合理的解，必须采用优化方法进行优化。

以分数阶数为设计变量，以最小平均相对误差为目标函数，分数阶累加灰色FMGM(1,)模型在于求解如下优化问题：

将分数阶累加生成算子编成函数RAGO.m，累减生成算子编成函数IRAGO.m. 以上述建模型方法调用分数阶累加生成算子函数RAGO.m，累减生成算子函数IRAGO.m编写模型求解函数FMGM.m作为目标函数。编写主程序main_FMGM.m,以已知数据为输入量，使用MATLAB优化设计函数fmincom或智能优化求解方法(如灰熵量子混沌粒子群优化算法[13])调用目标函数FMGM.m, 优化求解分数阶数，最后输出所需求的参数和模型的检验。模型求解后，要对模型进行检验以确定模型的是否合适。对MGM(1,)模型进行检验的方法常用的有3种[1−3]：残差检验、关联度检验以及后验差检验(略)。FMGM(1,)模型同样使用MGM(1,n)模型的检验方法进行检验。

2 应用实例

例1 TiN薄膜涂层的摩擦学性能分析。

在载荷600 N , 相对滑动速度分别为0.314，0.417，0.628，0.942和1.046 m/s条件下，TiN薄膜涂层试验结果如表1所示[14]。

表1 TiN薄膜涂层试验数据[14]

按本文方法得到滑动速度、摩擦因数、磨损率的MGM(1,3)模型，模型参数为

磨损率的模型值为(7.500 00，7.975 61， 8.397 03，9.301 81，11.47 06)，磨损率的相对误差为(0，−0.304 84%，−1.211 50%，−2.086 20%， 4.278 60%)，其相对误差绝对值的平均值为1.576 2 %。模型相对误差平均值为6.331 2%。模型检验为“好”。

按本文方法得到滑动速度、摩擦因数、磨损率的FMGM(1,3)模型，模型参数为

磨损率的模型值为(7.500 00，7.979 75， 8.447 13，9.384 2，10.975 8)，磨损率的相对误差为(0，−0.253 15%，−0.622 01%，−1.218 90%，−0.220 44%)，其相对误差绝对值的平均值为0.462 9%。模型相对误差平均值为5.969%。模型检验为“好”。

例2 CrN薄膜涂层的摩擦学性能分析。

在载荷为600 N , 相对滑动速度分别为0.314，0.417，0.628，0.942和1.046 m/s条件下，CrN薄膜涂层试验数据如表2所示。

表2 CrN薄膜涂层试验结果[14]

按本文方法得到滑动速度、摩擦因数、磨损率的MGM(1,3)模型，模型参数为

摩擦因数的模型值为(0.323 00，0.331 04， 0.338 22，0.34572，0.36325)，摩擦因数的相对误差为(0，0.011728%，−0.229 630%，−1.223 100%，−2.614 400%)，其相对误差绝对值的平均值为 0.815 77%，模型相对误差平均值为7.721%。模型检验为“好”。

按本文方法得到滑动速度、摩擦因数、磨损率的FMGM(1,3)模型，模型参数为

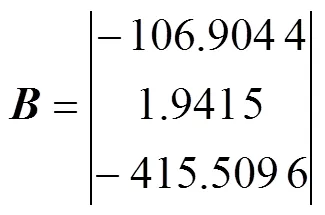
摩擦因数的模型值为(0.323 00，0.331 29， 0.337 84，0.348 26，0.370 27)，摩擦因数的相对误差为(0，0.088 321%，−0.343 180%，−0.497 030%， −0.731 220%)，其相对误差绝对值的平均值为 0.331 95%，模型相对误差平均值为4.499 2%。模型检验为“好”。由此可见，本文模型的适应性、有效性以及建立本模型的必要性。

3 结论

1) 将单变量分数阶累加灰色模型FGM(1,)推广到多变量情形，推导了多变量累加生成的计算公式，建立了多变量分数阶累加灰色模型FMGM(1,)，给出了基于最小二乘法估计模型参数。

2) 以分数阶数为设计变量，以最小平均相对误差为目标函数，建立优化模型，并编写了Matlab优化求解程序。

3) FMGM(1,)模型是一种状态模型,它是单变量的FGM(1,1)模型在多变量情形下的自然推广,旨在反映各变量间相互制约、相互促进的关系。FMGM(1,)模型不能代替FGM(1,1)模型,而是FGM(1,1)模型的扩展和补充。算例验证了本文所建模型的适应性和有 效性。

[1] LIU Sifeng, LIN Yi. Grey systems: theory and applications[M]. London: Springer-Verlag London Ltd, 2010: 3−8.

[2] 罗佑新, 张龙庭, 李敏. 灰色系统理论及其在机械工程中的应用[M]. 长沙: 国防科技大学出版社, 2001: 2−16. LUO Youxin, ZHANG Longting, LI Ming. Grey system theory and its application to mechanical engineering[M]. Changsha: National University of Defense technology Press, 2001: 2−16.

[3] 刘思峰, 党耀国, 方志耕, 等. 灰色系统理论及其应用[M]. 7版. 北京: 科学出版社, 2014: 1−5. LIU Sifeng, DANG Yaoguo FANG Zhigeng, et al. Grey system theory and its application[M]. 7th ed. Beijing: Science Press, 2014: 1−5.

[4] MOGHADDAM T V, BIGDELI N, AFSHAR K. Tuning a fractional order PID controller with lead compensator in frequency domain[J]. World Academy of Science, Engineering and Technology, 2011, 51(1): 1277−1282.

[5] WU Lifeng, LIU Sifeng, YAO Ligen, et al. Grey system model with the fractional order accumulation[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(7): 1775−1785.

[6] FANG Shili, WU Lifeng, FANG Zhigeng, et al.Using fractional GM(1,1) model to predict the maintenance cost of weapon system[J]. Journal of Grey System, 2013, 25(3): 9−15.

[7] 吴利丰, 刘思峰, 姚立根. 基于分数阶累加的离散灰色模型[J]. 系统工程理论与实践, 2014, 34(7): 1822−1827. WU Lifeng, LIU Sifeng, YAO Ligen. Discrete grey model based on fractional order accumulate[J]. Systems Engineering: Theory & Practice, 2014, 34(7): 1822−1827.

[8] 孟伟, 曾波. 分数阶算子与灰色预测模型研究[M]. 北京: 科学出版社, 2015: 1−60. MENG Wei, ZENG Bo. Fractional order operator and grey prediction model[M]. Beijing: Science Press, 2015: 1−60.

[9] 翟军, 盛建明. MGM(1,)灰色模型及应用[J]. 系统工程理论与实践, 1997, 17(5): 109−113. ZHAI Jun, SHENG Jianming. MGM(1,) grey model and its application. Systems Engineering: Theory & Practice, 1997, 17(5): 109−113.

[10] 崔立志, 刘思峰, 吴正朋. 基于向量连分式理论的MGM(1,)模型[J]. 系统工程, 2008, 26(10): 47−51. CUI Lizhi, LIU Sifeng, WU Zenpeng. MGM(1,m) based on vector continued fractions theory[J]. Systems Engineering, 2008, 26(10): 47−51.

[11] HE Zheming, LUO Youxin. Application of new information multi-variable grey model NMGM(1,n) to the load-strain relation[C]//2009 International Conference on Intelligent Computation Technology and Automation (ICICTA 2009). Zhangjiajie, China, 2009: 236−239.

[12] 熊萍萍, 党耀国, 朱晖. 基于非等间距的多变量MGM(1,m)模型[J]. 控制与决策, 2011, 26(1): 49−53. XIONG Pingping, DANG Yaoguo, ZHU Hui. Research of modeling of multi-variable non-equidistant MGM(1,) model[J]. Control and Decision, 2011, 26(1): 49−53.

[13] LUO Youxin, CHE Xiaoyi, WANG Chao. Grey entropy quantum-behaved chaotic particle swarm optimization based on high-dimension multi-objective optimization design of mixed discrete variables[J]. Electronic Journal of Geotechnical Engineering, 2014, 19(Z2): 10167−10178.

[14] 刘清平,徐笑词, 何友成. 薄膜涂层摩擦学性能的灰色分析与预测[J]. 润滑与密封, 2003, 28(4): 53−55, 58. LIU Qingping, XU Xiaoci, HE Youcheng. The grey forecast on the tribological behaviors of the film[J]．Lubrication Engineering, 2003, 28(4): 53−55, 58.

(编辑 杨幼平)

Multivariable grey model FMGM(1,) with fractional order accumulationand its application

LUO Youxin

(Hunan Province Cooperative Innovation Center for the Construction & Development of Dongting Lake Ecological Economic Zone, Hunan University of Arts and Science, Changde 415000, China)

After analyzing the fractional order AGO and IAGO of single variable, formula of multivariable fractional order AGO was deduced; the multivariable grey model FMGM(1,) with fractional order accumulation was established; the model parameter estimation based on least square method was derived. By taking fractional order and minimum average relative error as design variable and object function, the optimal model was established and the solution program based in Matlab was written. As natural promotion of single variable model FGM(1,1), multivariable grey model FMGM(1,) with fractional order accumulation reflected the interaction of variables. At last, the numerical example was given to indicate correctness and effectiveness of the model.

multivariable grey model FMGM(1,) with fractional order accumulation; optimization; least square method; model parameter estimation

10.11817/j.issn.1672−7207.2017.10.018

N94

A

1672−7207(2017)10−2686−05

2016−10−25；

修回日期：2017−01−25

湖南省“十二五”重点建设学科(湘教发[2011]76)、湖南省教育厅产业化培育项目(15CY008)、湖南省战略性新兴产业科技攻关类项目(2014GK1043) 、湖南省高校产学研合作示范基地(湘教通[2014]239)(Project (XJF2011[76]) supported by the Grant of the 12th Five-Year Plan for the Construct Program of the Key Discipline (Mechanical Design and Theory) in Hunan province; Project (15CY008) supported by Industrialization Development Project of Technological Achievements of Universities in Hunan Province; Project (2014GK1043) supported by Hunan Major Special Projects of Science and Technology; Project (XJT [2014] 239) supported by Cooperative Demonstration Base of Universities in Hunan, “R & D and Industrialization of Rock Drilling Machines”)

罗佑新，教授，从事不确定性系统理论、优化设计、机构学及其CAD等研究； E-mail:LLYX123@126.com