基于遗传算法的气象观测数据区间值属性约简算法

郑忠仁，程 勇，王 军,，钟水明，徐利亚

(1.南京信息工程大学 计算机与软件学院，南京 210044； 2.南京信息工程大学 信息化建设与管理处，南京 210044；3.九江学院 信息科学与技术学院，江西 九江 332005)(*通信作者电子邮箱zrzheng@foxmail.com)

基于遗传算法的气象观测数据区间值属性约简算法

郑忠仁1*，程 勇2，王 军1,2，钟水明1，徐利亚3

(1.南京信息工程大学 计算机与软件学院，南京 210044； 2.南京信息工程大学 信息化建设与管理处，南京 210044；3.九江学院 信息科学与技术学院，江西 九江 332005)(*通信作者电子邮箱zrzheng@foxmail.com)

针对气象观测数据采集目的性弱、数据冗余度较高以及观测数据区间化中单值较多、等价类划分精度低的问题，提出一种基于遗传算法的气象观测数据区间值属性约简算法(MOIvGA)。首先，通过改进区间值相似度，使其能够同时适用于单值等价关系判断和区间值相似度分析；其次，通过改进自适应遗传算法，提高其收敛性；最后，通过仿真实验证明，相对于运行自适应遗传属性约简(AGAv)算法求解最优值，所提算法迭代代数减少了22代；在区间长度为1 h降水分类中，基于依赖度的区间值决策表λ-约简(MOIvGA)平均分类准确率比RIvD算法提高了6.3%，对无雨的预测准确率提高了7.13%；同时约简后的属性子集显著提高了分类准确率。由此可见，MOIvGA在区间值气象观测数据分析中能够提高收敛速度以及分类准确率。

气象观测数据；属性约简；区间值相似度；遗传算法; 属性子集

随着信息化进程的加快和现代化探测仪、传感器等信息采集技术不断更新，以及人们对气象服务的需求迅速增加，气象监测的密度和频率也随之大幅增加，数以万计的气象观测数据成倍地增长，气象大数据的格局已经形成[1]。气象观测数据规模的迅速增长，不仅表现在数量上的增加，同时数据的维数也在急剧增加，即形成所谓的高维数据[2]。

由于气象观测数据在采集时目的性较弱，同时天气现象的发生往往是由属性集中的一部分的变化引起的，因此在气象观测大数据中属性的冗余度较大。粗糙集理论作为一种处理模糊、不确定信息的数学工具，其核心内容之一就是属性约简[3]。属性约简是指在保持知识库分类能力不变的前提下，删除冗余的属性，简化信息系统，从而方便知识获取[4]。气象数据作为一种典型的时间序列行为数据，在相当一段时空范围内相关性较大。然而属性约简处理对象都是离散型的，必须将气象要素数据离散为单值数据，但这样往往会造成处理结果在一定程度上物理意义不明确，造成知识的遗漏[5]。

因此，本文提出一种基于气象数据离散化的区间值信息系统分析方案。相比于单值数据，属性区间化不仅可以减少计算量，还可以反映气象要素在该段时间内的变化情况；由于温、湿度等气象要素在相当长的时间内变化较小，随着采样频率的增加，属性区间化可以有效地降低相邻时间内同一属性的值变化不大以及个别属性值缺失对分类的影响；并且对于温、湿度等连续性属性可以根据区间值的长度判断该段时间内是否存在异常数据。

1 相关工作

1982年粗糙集理论提出，经过几十年的发展，粗糙集理论广泛应用于各领域，并取得了丰硕的成果[6-12]，例如模式识别与分类[10]、股票预测分析[11]、决策分析[12]等。属性约简作为粗糙集理论研究的重点，已有证明求解最小属性约简是一个NP-hard问题，即当数据量增大时，问题复杂度将以指数增长[13]，这也给传统的属性约简算法带来了挑战。因此，当前属性约简的研究主要集中在基于启发式的属性约简。

目前，基于启发式的单值信息系统的属性约简已经很多。许多学者已经逐渐意识到传统属性约简的不足，开始深入研究区间值信息系统的属性约简。文献[14]以一种优势关系来判定区间值的优劣，一定程度上提高了算法的准确率。文献[15]提出基于属性依赖度和互信息的区间值启发式约简，并将其应用于电力大数据中；但该文中仅依靠单个阈值限制等价类的划分，误分率较高。文献[16]提出了一种α-极大相容类的概念，有效地提高了分类的近似精度；但其求取两个区间的相似率分类粒度较粗，容易造成知识遗漏。文献[17]提出了容差关系的概念，该方法有效利用区间值的特性，一定程度上降低了误分率，提高了分类精度。

为了进一步提高属性约简的效率，融通其他优化算法显得十分必要。遗传算法作为一种模拟生物进化的启发式搜索算法，具有极好的全局搜索能力，同时具有自组织性、自适应性以及并行性等特点；随着多年来不断地发展与完善，效率也大大提高，也使其在应用领域都取得令人满意的效果。而标准的遗传算法交叉概率和变异概率通常使用常量系数，导致收敛速度慢和容易早熟等问题。

基于此，本文提出了基于遗传算法的气象观测数据区间值属性约简算法(Meteorological Observation data Interval-value attribute reduction algorithm based on Genetic Algorithm, MOIvGA)。针对气象观测数据的时空相关性，提出将属性值域区间化，从而讨论区间值信息系统，增强算法的实用性；针对气象观测数据采集量大、属性冗余度高等特点，利用遗传算法的并行性和全局搜索能力等优势，将自适应遗传算法和粗糙集理论相结合应用于气象观测数据进行属性约简，提高了约简算法的性能。

2 基于区间值的属性依赖度遗传属性约简

2.1 区间值决策表的概念和性质

2.1.1 区间值决策表概念

2.1.2 区间值决策表的相容类

粗糙集理论的核心是等价关系，对于单值决策表往往通过属性值的等价关系实现对论域的划分[15]。而与经典粗糙集中的决策表(属性值为单值)不同，在区间值决策表中，条件属性值很难满足完全等价，因此，通过等价关系对论域进行划分就不再适用。为此，将区间值相似度引入到区间值决策表，用两个区间的共同部分的大小来衡量区间的相似程度，从而通过区间值相似度实现对论域的划分。

区间化的气象观测数据不同于其他区间值决策表，由于气象观测数据中存在一部分的随机性数据，例如降雨量、能见度等，当这些气象要素作为条件属性时，可能存在恒为单值的情况，例如降水量为条件属性时，无雨的天气属性值均为0。如果忽略这种情况，势必影响分类的质量。因此，本文将区间值相似度定义如下：

(1)

(2)

其中，card(*)表示区间值的长度。式(1)将单值数据视为区间值数据中的一个特例，此时的相似度公式同样能够满足判断单值属性的等价关系。相似度作为衡量两个区间值的近似等价程度，为区间值决策表论域的划分提供了一种有效的度量标准。

文献[16]中，算法仅通过α一个阈值来限制等价类的划分可能导致某些知识被遗漏。例如α=0.7时，对象xi和xj的相似度为(0.9,0.9,0.9,0.69)，这时依据文献[16]，对象xi和xj是不相容的。而事实上这种情况下的相容概率并不比(0.7,0.7,0.7,0.7)差，因此本文将近似等价关系的限制条件中加入了联合相似度。定义如下：

定义3 设区间值决策表S=(U,C∪D,V,f)，属性子集A⊆C，α∈[0,1]为给定阈值，将区间值决策表中对象xi和xj关于属性A的α-近似等价关系定义为：

(3)

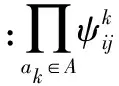
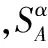
2.1.3 区间值决策表的属性依赖度

上面介绍的定义和性质都是围绕区间值决策表的条件属性，并没有涉及到决策表的决策属性。定义区间值决策表的决策属性D关于条件属性子集A的正域为：

定义4[18]设区间值决策表S=(U,C∪D,V,f)，α∈[0,1]，决策属性D对论域的划分为{ω1,ω2,…,ωn}，任意条件属性子集A⊆C，则决策属性D关于A的正域为：

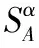
(4)

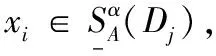
定义5[15]正域的大小反映了分类问题在给定属性空间中的可分离程度。为了度量条件属性与决策属性关系的重要程度，定义决策属性D相对于条件属性子集A的α-依赖度为：

(5)

定义6[15]设区间值决策表S=(U,C∪D,V,f)，A⊆C，α∈[0,1]，如果属性子集A满足以下条件，则称属性子集A是条件属性C的一个α-约简:

条件1)要求属性子集保持决策表的分类能力不变；条件2)要求约简中删除冗余属性。这与粗糙集属性约简的定义完全一致。

2.2 遗传算法

遗传算法以模拟生物进化过程来寻找最优解，其一般由编码、适应度函数、选择算子、交叉算子以及变异算子五部分组成[19]。

2.2.1 编码方式

本文采用二进制染色体定长编码的方式，即每个染色体都对应一个条件属性子集，染色体的每一位基因对应一个条件属性。基因位取“0”和“1”分别表示不选择和选择对应的条件属性。例如，在决策表S中，每个对象有6个条件属性{a1,a2,a3,a4,a5,a6}。若求得一个可能的约简为{a2,a3,a5,a6}，则染色体应表示为011011。

2.2.2 适应度函数

适应度函数是遗传算法的关键步骤，控制着群体的进化方向，也是评价和选择染色体的重要依据。根据粗糙集属性约简的定义可知，适应度函数的目标是在满足原分类质量不变的同时使得染色体属性个数尽可能少，因此，本文将属性依赖度和条件属性个数引入到适应度函数中，定义如下：

(6)

2.2.3 选择算子

选择算子是指以何种方式选择群体中的染色体来进行交叉和变异操作。本文采用适应度比例选择方法，即轮盘赌的方式选择染色体，即每个染色体vi的适应度值占所有染色体适应度值总和的比例。具体定义如下：

(7)

以此作为染色体vi被挑选出来进行下一步操作。

2.2.4 交叉算子和变异算子

传统遗传算法的交叉概率和变异概率均是常量，很容易导致收敛速度慢和早熟等问题。自适应遗传算法则采用动态的交叉概率和变异概率一定程度上避免了这些现象[20]。算法早熟主要是因为种群中优良染色体大量繁殖，以致占据整个种群，破坏了群体的多样性。标准自适应遗传算法采用种群中最大适应度值和平均适应度值的差作为衡量收敛性的度量，而早熟往往是由适应度值较大的染色体引起的，为了降低较差染色体对收敛性的影响，提出用最大适应度值与适应度值大于平均适应度值染色体的平均适应度值差值作为衡量标准。同时从算法的进化过程来看，随着算法的进行交叉概率和变异概率应该逐渐变小。

基于此，本文将交叉概率Pc和变异Pm分别定义如下：

(8)

(9)

其中:fmax为当代种群中最大的适应度值，ftmax为当代种群中适应度值大于平均适应度值染色体的平均适应度值；G为种群的进化代数；b1、b2分别代表交叉概率和变异概率关于进化代数的变化曲率，通常均取最大遗传代数的倒数；C1和M1分别为交叉概率和变异概率的收敛极限；l1为控制因子，通常取0.2。

2.3 MOIvGA

属性依赖度作为条件属性对决策属性重要性的度量，描述了条件属性对分类的贡献，因此可以作为属性约简中属性重要程度的评价标准。而遗传算法作为一种隐含并行性的启发式搜索算法，常用来解决复杂的优化问题。根据属性约简的定义将属性依赖度和条件属性个数作为遗传算法适应度函数的参数，控制种群的进化方向。从而将粗糙集理论和遗传算法相结合，借助遗传算法模拟生物的进化过程，可使得种群不断优化，并在优化过程中寻找全局最优解。

算法1 基于遗传算法的气象观测数据区间值属性约简算法(MOIvGA)。

输入：S=(U,C∪D,V,f)，α、b1、b2、C1、M1、l1、λ；

输出：属性约简red。

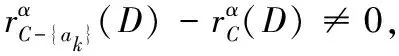
步骤3 对任意ak∈C，若ak∈Core(C)，即为核属性，则对应的染色体基因位为1；若ak∉Core(C)，则可随机选择，对应的染色体基因位为0或1。

步骤4 根据式(5)分别计算决策属性对群体中每个染色体的条件属性依赖度值，再由式(6)计算每个染色体的适应度值，并将染色体按适应度值的大小进行排序，以淘汰概率np淘汰适应度值较差的个体。

步骤5 进行选择操作；并根据式(8)的交叉概率Pc选择配对的染色体进行等基因片段交换操作。

步骤6 基本位变异，根据式(9)的变异概率Pm决定染色体是否进行变异操作，如果需要进行变异操作，则随机选择变异的基因位，当选择的属性为核属性时不发生变异，重新选取染色体其他属性进行变异操作。

步骤7 判断是否达到最大迭代次数和群体连续三代适应度是否满足||Fi-2-Fi-1|-|Fi-1-F||<ε，如果满足一个则停止执行，并输出最优染色体；否则转步骤4。

α值需要根据数据的具体情况设定，其值的大小直接影响了分类的结果。α值越大，要求越严格，即相容类元素个数越少。为了检验MOIvGA的性能，对气象观测数据中影响降水量的相关因素进行属性约简测试，并且与文献[15]中的基于依赖度的区间值决策表λ-约简(λ-Reduction in Interval-valued decision table based on Dependence, RIvD)算法在算法性能方面进行了比较与评价。

3 实例分析

3.1 实验数据

气象观测数据是一种典型的时间序列数据，每年的降水多集中在4—7月份，为了降低地域等因素对降水的影响，本文实验仅采用相近四个气象站点2016年4—7月份采集的10万余条数据集，除去区站号、经纬度以及时间，共有26个属性(均为数值型)。并根据表1降水量等级划分表将观测数据中降水量改为对应的等级，形成决策属性，从而得到一个大型的决策表。

表1 降水量等价划分表

属性约简是在不改变知识库分类能力的前提下，删除冗余属性，因此评价约简算法的性能还需用约简的属性子集进行分类预测，根据分类结果判断约简算法的优劣。在分类预测时，测试数据与训练数据时间间隔相同，将测试结果与测试数据实际的决策属性进行比较，统计预测正确的个数，整个过程采用十折交叉计算分类准确率。MOIvGA中C1、M1分别取0.12、0.01。

3.2 结果与分析

3.2.1 遗传算法收敛度

首先，为了验证MOIvGA中改进的自适应遗传算法的性能，与标准的自适应遗传属性约简(Adaptive Genetic Attribute Reduction, AGAv)算法对区间长度为2 h的观测数据运行比较。为了直观地比较算法的收敛过程，将算法的终止条件设置为满足最大迭代次数。由于种群初始化时，除核属性外是随机产生的，因此并不能保证两种算法的初始最佳个体相同；同时数据集的属性约简往往不止一个，因此需要对两种算法进行多次实验，选取约简属性子集相同的两次进化过程进行比较。选取的两次进化过程如图1所示。

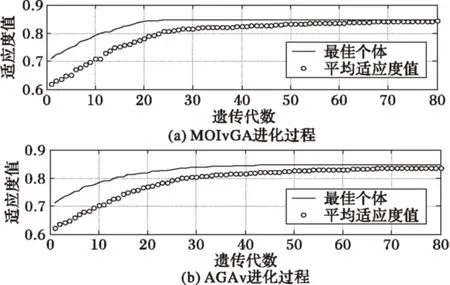
图1 最佳个体适应度值变化过程

由图1可知，MOIvGA和AGAv算法分别在23代和45代收敛到最优解。根据图中平均适应度值变化过程可以看出，MOIvGA的进化也优于AGAv算法。

为了更直观比较两种算法的进化过程，提出用遗传算法收敛率来比较两种算法的寻优效率，收敛率为当代最佳个体适应度值和第一代最佳个体适应度值的差值与最终收敛值的比值。两种算法的收敛率变化如图2所示。

图2 两种算法收敛率比较

由图2可知，两种算法最终的收敛率并未重合。这是由于两种算法的初始化结果不同，即第一代最佳个体不同。从图2还可以看出在进化的初期，两种算法的收敛率差异不大，但随着进化过程的进行，MOIvGA以更快的收敛率达到最优解。这是由于前期种群多样性复杂，种群中染色体变化较大。但随着进化的进行，MOIvGA的保优操作以及选择操作的优势逐渐突显出来，从而提高了算法的收敛速度。

3.2.2 不同时间间隔约简的准确率

为了考察MOIvGA在气象观测数据中的有效性，将MOIvGA和文献[15]中RIvD算法分别对时间间隔为30 min、1 h、2 h、3 h、6 h、12 h数据集进行约简操作，并对约简的属性子集在K最近邻(K-Nearest Neighbor,KNN)(K=3)分类器中进行分类预测，两种算法的区间相似度均取0.7。结果如图3所示。

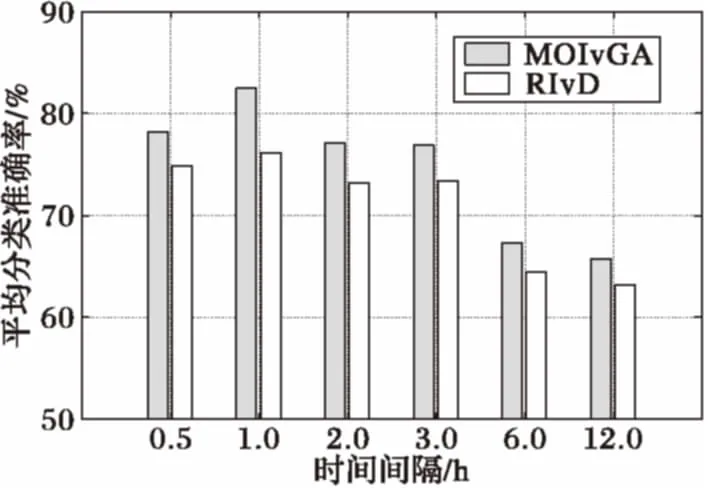
图3 不同时间间隔下的平均分类准确率

从图3可以看出在时间间隔小于3 h的情况下，平均分类准确率均都能达到70%以上，间隔为1 h的情况下两种算法的分类准确率均达到最高，并且 MOIvGA比RIvD算法提高了6.3%。而在6 h和12 h的时间间隔下，两种算法的分类准确率都明显下降。主要是由于气象数据在相近时间内的时空相关性较大，随着时间间隔的增长，变化性因素较大，时空相关性的特征有所减弱；同时随着间隔的增长，数据量大量减少。从图中还可以看出MOIvGA整体的平均分类准确率都优于RIvD算法，这是由于气象数据在区间化后仍然有较多的单值数据，而RIvD算法并不能处理单值数据，以及MOIvGA中加入了联合相似度的限制，使得MOIvGA约简效果更好。

3.2.3 约简前后数据准确率

为了进一步比较约简后的属性子集与原数据的分类能力，选取MOIvGA和RIvD算法对时间间隔为1 h约简结果在KNN(K=2)分类器中进行降水等级分类预测，两种算法的约简结果如表2所示。在分类预测过程中的测试数据和训练数据均为同一数据集。分类结果如图4所示。

由表2可知，MOIvGA剩余属性个数少于RIvD算法。由于RIvD算法采用的是以属性重要度为指标的前向搜索算法，即每次从属性重要度中选择最大的属性逐个加入约简集合中。而MOIvGA则用属性依赖度和属性个数两个因素控制进化方向，并借助遗传算法将多个个体作为可能解，从而在全局范围内寻找最优解。因此一般情况下MOIvGA的约简结果优于RIvD算法。

表2 MOIvGA和RIvD算法的约简结果

由图4可知，两种算法约简的属性子集的分类准确率均高于原数据。在无雨预测中，本文算法的分类准确率比RIvD算法提高了7.13%，比原数据提高了14.24%。但随着降水等级的增加，分类准确率逐渐降低。这是由于分类预测准确率和样本数据有着显著的关系，随着降水等级的增加，对应的样本数目大量减少，蕴含的信息量也大幅度减少，因此分类准确率也就很低。

图4 KNN分类准确率

4 结语

本文针对气象观测数据时空相关性较强的特点，提出将气象观测数据区间化，并借助改进的自适应遗传算法寻找全局最优解。通过实验证实，MOIvGA能够以较快的速度收敛到最优解。对不同区间长度的气象观测数据降水影响因素约简中，MOIvGA在间隔为1 h的情况下优势最明显。与原数据的分类预测算法相比，MOIvGA约简的属性子集有明显的提高。MOIvGA在不影响数据的分类能力下，有效地降低了属性维度，但单个节点的运算能力仍然有限，后期将围绕如何在Map-Reduce分布式平台下实现算法的并行化处理，从而应用在实际的气象大数据环境。

References)

[1] 白雪.气象领域事件挖掘相关问题的研究[D].上海:复旦大学,2013:1-10.(BAI X. Research on relevant issues of event mining in meteorological field [D]. Shanghai: Fudan University, 2013: 1-10.)

[2] 赵方霞.基于气象数据的数据挖掘算法研究[D].北京:北方工业大学,2011:1-14.(ZHAO F X. Research on data mining algorithm based on the meteorological data[D]. Beijing: North China University of Technology, 2011: 1-14.)

[3] LI P, WU J, QIAN H. Groundwater quality assessment based on rough sets attribute reduction and TOPSIS method in a semi-arid area, China [J]. Environmental Monitoring and Assessment, 2012, 184(8): 4841-4854.

[4] CHANG S. A novel attribute reduction method based on rough sets and its application [J]. International Journal of Advancements in Computing Technology, 2012, 4(3): 99-104.

[5] 于莹莹,曾雪兰,孙兴星.优势关系下的区间值信息系统及其属性约简[J].计算机工程与应用,2011,47(35):122-124.(YU Y Y, ZENG X L, SUN X X. Interval-valued information system based on dominance relation and its attribute reduction [J]. Computer Engineering and Applications, 2011, 47(35): 122-124.)

[6] ZENG A, PAN D, ZHENG Q L, et al. Knowledge acquisition based on rough set theory and principal component analysis [J]. IEEE Intelligent Systems, 2006, 21(2): 78-85.

[7] JEON G, KIM D, JEONG J. Rough sets attributes reduction based expert system in interlaced video sequences [J]. IEEE Transactions on Consumer Electronics, 2006, 52(4): 1348-1355.

[8] SINHA D, LAPLANTE P. A rough set-based approach to handling spatial uncertainty in binary images [J]. Engineering Applications of Artificial Intelligence, 2004, 17(1): 97-110.

[9] KAYA Y, UYAR M. A hybrid decision support system based on rough set and extreme learning machine for diagnosis of hepatitis disease [J]. Applied Soft Computing, 2013, 13(8): 3429-3438.

[10] ASHARAF S, MURTY M N. A rough fuzzy approach to web usage categorization [J]. Fuzzy Sets & Systems, 2004, 148(1): 119-129.

[11] CHENG C H, CHEN T L, WEI L Y. A hybrid model based on rough sets theory and genetic algorithms for stock price forecasting [J]. Information Sciences, 2010, 180(9): 1610-1629.

[12] GRECO S, MATARAZZO B, SLOWINSKI R. Rough sets theory for multicriteria decision analysis [J]. European Journal of Operational Research, 2001, 129(1): 1-47.

[13] ZHAO H, MIN F, ZHU W. Test-cost-sensitive attribute reduction based on neighborhood rough set [C]// Proceedings of the 2011 IEEE International Conference on Granular Computing. Piscataway, NJ: IEEE, 2011: 802-806.

[14] 杨青山,王国胤,张清华,等.基于优势关系的区间值粗糙集扩充模型[J].山东大学学报(理学版),2010,45(9):7-13.(YANG Q S, WANG G Y, ZHANG Q H, et al. The interval-valued rough set extended model based on the dominance relation [J]. Journal of Shandong University (Natural Science), 2010, 45(9): 7-13.)

[15] 徐菲菲,雷景生,毕忠勤,等.大数据环境下多决策表的区间值全局近似约简[J].软件学报,2014,25(9):2119-2135.(XU F F, LEI J S, BI Z Q, et al. Approaches to approximate reduction with interval-valued multi-decision tables in big data [J]. Journal of Software, 2014, 25(9): 2119-2135.)

[16] 张楠,苗夺谦,岳晓冬.区间值信息系统的知识约简[J].计算机研究与发展,2010,47(8):1362-1371.(ZHANG N, MIAO D Q, YUE X D. Approaches to knowledge reduction in interval-valued information systems [J]. Journal of Computer Research and Development, 2010, 47(8): 1362-1371.)

[17] 陈子春,秦克云.区间值信息系统在变精度相容关系下的属性约简[J].计算机科学,2009,36(3):163-166.(CHEN Z C, QIN K Y. Attribute reduction of interval-valued information system based on variable precision tolerance relation [J]. Computer Science, 2009, 36(3): 163-166.)

[18] 贾凡,薛佩军,许嘉.决策区间值信息系统的交互相容关系及属性约简[J].计算机科学,2012,39(s3):245-248.(JIA F, XUE P J, XU J. Interactive tolerance relation in interval-valued decision table and attribute reduction [J]. Computer Science, 2012, 39(s3): 245-248.)

[19] 邓刚锋,黄先祥,高钦和,等.基于改进型遗传算法的虚拟人上肢运动链逆运动学求解方法[J].计算机应用,2014,34(1):129-134. (DENG G F, HUANG X X, GAO Q H, et al. Solution method for inverse kinematics of virtual human’s upper limb kinematic chain based on improved genetic algorithm [J]. Journal of Computer Applications, 2014, 34(1):129-134.)

[20] 孙越泓,魏建香,夏德深.基于自适应遗传算法的B样条曲线拟合的参数优化[J].计算机应用,2010,30(7):1878-1882.(SUN Y H, WEI J X, XIA D S. Parameter optimization for B-spline curve fitting based on adaptive genetic algorithm [J]. Journal of Computer Applications, 2010, 30(7): 1878-1882.)

Interval-valueattributereductionalgorithmformeteorologicalobservationdatabasedongeneticalgorithm

ZHENG Zhongren1*, CHENG Yong2, WANG Jun1,2, ZHONG Shuiming1, XU Liya3

(1.SchoolofComputer&Software,NanjingUniversityofInformationScienceandTechnology,NanjingJiangsu210044,China;2.InformationConstructionandManagementDepartment,NanjingUniversityofInformationScienceandTechnology,NanjingJiangsu210044,China;3.SchoolofInformationScienceandTechnology,JiujiangUniversity,JiujiangJiangxi332005,China)

Aiming at the problems that the purpose of the meteorological observation data acquisition is weak, the redundancy of data is high, and the number of single values in the observation data interval is large, the precision of equivalence partitioning is low, an attribute reduction algorithm for Meteorological Observation data Interval-value based on Genetic Algorithm (MOIvGA) was proposed. Firstly, by improving the similarity degree of interval value, the proposed algorithm could be suitable for both single value equivalence relation judgment and interval value similarity analysis. Secondly, the convergence of the algorithm was improved by the improved adaptive genetic algorithm. Finally, the simulation experiments show that the number of the iterations of the proposed algorithm is reduced by 22, compared with the method which operated AGAv (Adaptive Genetic Attribute reduction) algorithm to solve the optimal value. In the time interval of 1 hour precipitation classification, the average classification accuracy of the MOIvGA (λ-Reduction in Interval-valued decision table based on Dependence) algorithm is 6.3% higher than that of RIvD algorithm; the accuracy of no rain forecasting is increased by 7.13%; at the same time, the classification accuracy can be significantly impoved by the attribute subset

by operating the MOIvGA algorithm. Therefore, the MOIvGA algorithm can increase the convergence rate and the classification accuracy in the analysis of interval value meteorological observation data.

meteorological observation data; attribute reduction; interval-value similarity; genetic algorithm; attribute subset

2017- 03- 17;

2017- 04- 25。

国家自然科学基金资助项目(61402236, 61373064)； 江苏省“六大人才高峰”项目(2015-DZXX-015)； 赛尔网络下一代互联网技术创新项目(NGⅡ20160318)。

郑忠仁(1991—)，男，江苏淮安人，硕士研究生，主要研究方向：大数据； 程勇(1980—)，男，重庆人，高级工程师，博士，CCF会员，主要研究方向：无线传感器网络、大数据； 王军(1970—)，男，安徽铜陵人，教授，博士，CCF会员，主要研究方向：无线传感器网络、大数据；钟水明(1971—)，男，江西瑞金人，讲师，博士，CCF会员，主要研究方向：人工神经网络、模式识别、数据挖掘； 徐利亚(1984—)，男，江西九江人，讲师，博士，主要研究方向：无线传感器网络、大数据。

1001- 9081(2017)09- 2678- 06

10.11772/j.issn.1001- 9081.2017.09.2678

TP18; TP301.6

A

This work is partially supported by the National Natural Science Foundation of China (61402236, 61373064), the “Six Talent Peaks Project in Jiangsu Province (2015-DZXX-015), CERNET Innovation Project (NGⅡ20160318).

ZHENGZhongren, born in 1991, M. S. candidate. His research interests include big data.

CHENGYong, born in 1980, Ph.D., senior engineer. His research interests include wireless sensor network, big data.

WANGJun, born in 1970, Ph. D., professor. His research interests include wireless sensor network, big data.

ZHONGShuiming, born in 1971, Ph. D., lecturer. His research interests include artificial neural network, pattern recognition, data mining.

XULiya, born in 1984, Ph. D., lecturer. His research interests include wireless sensor network, big data.