移动传感网分布式连通按需覆盖部署方法
2017-11-15毛凌楚赵海涛
毛凌楚,赵海涛
(国防科学技术大学 电子科学与工程学院,长沙 410073)(*通信作者电子邮箱maolc@126.com)
移动传感网分布式连通按需覆盖部署方法
毛凌楚*,赵海涛
(国防科学技术大学 电子科学与工程学院,长沙 410073)(*通信作者电子邮箱maolc@126.com)
针对移动传感器网络监测区域中目标覆盖所需传感器数不同且各目标之间没有形成通路的问题,提出了通过虚拟力方法实现对不同目标的按需覆盖方法。根据不同目标的覆盖需求设置对传感器节点的基于万有引力的吸引力、节点之间基于库仑力的斥力以及目标之间的引力线,节点在虚拟合力的引导下覆盖目标或连接成通路。仿真结果显示所提方法与已有代表性算法相比收敛时间短,节点移动公平性高达99%,且GPS误差的影响能够控制在1%以下,可实现稀疏或密集初始条件下按需覆盖的分布式快速部署。
移动传感网;按需覆盖;虚拟力;引力线
0 引言
移动传感器网络在现代信息技术中是必不可少的一部分。通常人为部署传感器时会以对区域的均匀覆盖为目标,但是在移动传感网的现实应用中,对于一片区域的覆盖需求通常不是均匀的。这就是说,在监测区域中存在部分目标由于需求较高需要更多的节点对其进行重点覆盖,而另一些目标则可以部署相对较少的节点。那么,根据实际的覆盖需求调整节点的部署就可以实现对监测区域的按需覆盖,这样的覆盖方案更符合实际应用。在实际的应用中,传感器网络对于信息传递的通畅有一定的要求,需要各传感器节点能够连通起来,在整个网络的各个目标之间保持通信链路,这在网络的部署中也是要考虑的一个重要的问题。例如在无网络覆盖的地方或因大型集会等突发状况需要临时提供网络服务时,根据任务需求按需部署网络并保证网络的连通是值得注意的一个应用场景;或者在现代信息化战场上的无人机集群等多节点的战场环境感知,这些都是潜在的应用场景。
在这方面前人做了许多的研究工作。文献[1]提出了一种基于Voronoi多边形[2-3]形心的部署策略,将对区域的覆盖转换为各节点对其所划分的Voronoi多边形的覆盖进行处理,但其对于质心[1]和区域划分的计算较复杂。文献[4]采用MW-Voronoi(Multiplicatively Weighted Voronoi)图分割目标区域,各节点在所受的虚拟力[5]的作用下运动,但由于子区间包含曲线边界,所以算法复杂度较大。文献[6]提出了一种基于VL(Voronoi Laguerre)图[7]分割的节点自主部署算法(Autonomous Deployment Algorithm, ADA),该算法需要将节点分为两类采用不同的方法进行处理,且需要全局信息支持。在采用虚拟力的方法上,Howard等[8]将运动机器人路径规划的虚拟势场[9-10]方法引入传感器节点的部署中,在移动节点的再部署中收获了较好的效果,但是其必须在所有节点始终保持联系的情况下执行。Zou[11]提出一种虚拟力算法,解决了节点初始随机部署后的自动完善网络覆盖性能的问题,可以均匀网络覆盖提高覆盖率,但是需要簇头节点控制,不能分布式部署[12]。文献[13]提出了一种基于虚拟力的传感器节点移动算法,该算法模拟自然界中的引力和斥力来指导节点的移动,适用于密集初始条件或稀疏初始条件,但收敛速度较慢,且最终形成的部署结构在各节点之间存在覆盖空洞。前人的研究针对不同的场景作了相应的优化,但是算法结构较复杂,且不能实现无缝覆盖。文献[14]提出结合传统的两种控制方法的半聚群控制方法,既能对目标进行集中覆盖,同时又保留一部分游离的节点去探索区域,使得覆盖更加合理。但是,该方法没有考虑到各目标之间的传感器节点的通信,整个网络没有连接成一个整体,增加了信息的收集和传递的成本。本文在文献[13]和[14]的基础上提出基于虚拟力场的移动传感器网络分布式连通按需覆盖部署方案,按覆盖需求设置目标对节点的引力和节点间的斥力,引入目标之间的引力线,通过节点的分布式计算和移动,实现对不同需求区域的动态按需覆盖和节点之间的通信连通,同时在无缝覆盖区域的前提下覆盖面积最大,且节点移动公平性较高,全球定位系统(Global Positioning System, GPS)误差容忍性较好。
1 问题描述
在一个二维矩形L×W平面监测区域Ω⊂R2内部署N个移动传感器节点S={s1,s2,…,si,…,sN}。对该平面区域,以矩形左下角的顶点为坐标原点,水平向右为X轴正方向,竖直向上为Y轴正方向建立笛卡尔坐标系。对S中任意节点si,其位置坐标为(xi,yi),感知范围为以节点位置为圆心,感知半径R为半径的圆,其通信范围为半径2R的圆。区域中需要节点覆盖的M个目标记为C={c1,c2,…,ck,…,cM}(此处的目标既可以是单个个体,也可以是一片热点区域的几何或业务中心),这是节点仅需要知道的全局信息(在节点散播前预置,或通过接收广播获得),其他的信息全部通过分布式交互获得(例如节点通过广播带有其位置信息的HELLO包给邻居节点,通信范围内的邻居节点返回带有本身位置信息的ACK使得节点之间可以共享位置信息。而HELLO包在许多通信协议中都有广泛应用,这也不会增加网络的额外负载。因此,整个系统不需要中心控制,节点的位置信息通过节点之间的交互传递,是完全分布式的)。初始时将若干节点或集中或分散地随机抛撒入区域中,之后节点根据分布式计算逐渐调整部署,使得所有节点根据目标的覆盖需求大小对其进行相应的覆盖,对覆盖需求高的部署更多节点,反之则部署较少节点。部署完成时,要求节点覆盖的范围尽可能大,节点之间不能出现覆盖空洞,且各目标之间的节点应保持通信连接。
2 按需部署算法
对于移动传感网中节点自主按需覆盖部署,本文借鉴了虚拟力体系的思想,但是本文的设计思路和应对场景与之前的研究有所不同:1)不同于以往均匀的覆盖,本文针对的场景是目标的动态按需覆盖,更符合实际应用场景;2)本文的方法可以保持各个目标之间节点的通信连接;3)传统方法所借鉴的虚拟力不适用于动态按需覆盖场景,本文重新进行了设计,且本文的虚拟力设置思路不是通常的受力平衡,而是用虚拟力指导节点运动,最后利用几何方法确定节点间的距离;4)本文的部署方法同时适用于初始时节点是集中的和随机分散的情况。
2.1 虚拟力设置
对于处在虚拟力场中的节点而言,如果只受到单一的虚拟力是难以趋于稳定的。所以在这个虚拟力场中,应该有多种虚拟力共同作用来使节点部署到预期的状态。虚拟力通常可以分为两类:引力和斥力。引力可以使节点聚集,将节点引向需要其部署的位置。节点间的斥力可以使得节点的分布分散开来,减少过多的重复覆盖,提高覆盖率。应该明确的是,虚拟力都是矢量,要考虑大小和方向。
关于虚拟力整体的设计思路是:由目标产生范围较大但是大小较小的引力,将区域中的节点吸引到目标附近;在节点间距离较近时,各节点两两之间产生相互的斥力,斥力的值较大,但作用范围较小,通过控制斥力的作用范围来调整节点之间的分散程度;另外,引入连接两个目标的虚拟引力线,节点受到引力线的引力向引力线运动,并在引力线上连成一条线,像一条电话线将两个目标周围的节点连接起来。
如图1为一种可能的节点受力情况示意。
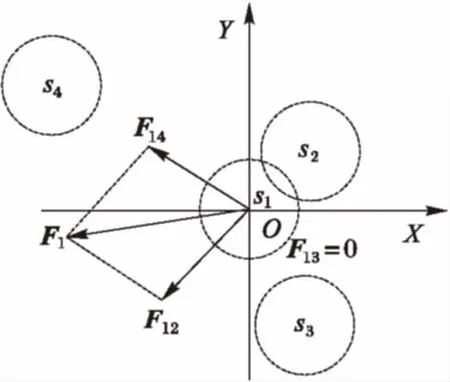
图1 一种虚拟力示例
图1中所示s1、s2、s3、s4为四个节点,s1和s2之间由于距离过近产生了斥力F12,s1和s4之间由于距离过远产生了引力F14,而节点s1和s3之间的虚拟力F13为零,故s1所受合力如图中F1所示。
2.1.1 目标引力
需要覆盖的目标产生在监测区域内指向目标的引力场,在它的影响下,监测区域内所有的节点都会受到指向目标的引力,将节点“拉”向目标运动,从而使这些节点聚集在目标的附近。
1)对于引力的方向,显然目标产生的引力方向在监测区域内任何一点都应该是指向目标的。
2)对于引力的大小,借鉴万有引力定律,可以设置为与到目标的距离的平方成反比,比例系数则反映覆盖需求。这就意味着,距离目标越远,节点所受的引力越小。特别是这样的设置在按需覆盖中应用更合理,因为在按需覆盖中有多个目标待考察,以两个目标为例,若节点所受的引力大小与其和目标的距离呈线性关系的话,就会导致节点不聚集在目标附近,而是聚集在两个目标连线之间的某一点上。而采用上述设置方法时,节点会向引力较大的目标方向移动,在移动过程中,其所受到的目标方向的引力逐渐变大,而来自其他目标的引力迅速减小,可以聚集在产生引力的目标附近,避免了节点停留在目标之间某处。
由于在平面坐标系中研究虚拟力场,所以对于虚拟力矢量来说,表示成沿坐标轴的分量更加清晰明了,也便于计算。那么,目标产生的虚拟引力就可以表示为:
X方向:
Fax=Ka×(Δxa/d2)
(1)
Y方向:
Fay=Ka×(Δya/d2)
(2)
其中:Ka为引力系数,d为目标到基站的距离,Δxa和Δya分别表示由节点指向中心的单位方向矢量的X和Y方向的分量。
式(1)、(2)中的引力系数Ka可以根据不同的目标设置不同的值,甚至可以利用相关参数建模成量化的通信或感知等需求。当需求变化时,节点受力随之变化,从而动态调整。这一引力的设置方法可以同时适用于初始情况下节点分布较集中的密集初始条件或节点分布较分散的稀疏初始条件,有利于网络的连通性。
2.1.2 节点斥力
仅有引力的作用会导致节点重叠在一起,为了解决这一问题,引入节点间的相互斥力使节点彼此分散开以提高覆盖率。与引力不同,斥力的产生作用的范围较小,只有在两节点距离较近时才产生作用。以下将以一对邻居节点si和sj为例,分别对斥力的方向、大小和作用范围进行讨论。
1)对于节点间斥力方向的设置,是沿两节点连线指向外侧,对于节点si来说,它受到的来自邻居节点sj的斥力的方向就是从sj指向si的。
2)对于节点间斥力的大小,借鉴库仑力思想,将其大小设置为与两节点间的距离平方成反比,比例系数设置为远大于目标引力的值。这样设计节点间的斥力要比目标产生的引力大得多,以至于可以将节点视为刚体,经过引力吸引到一起之后被斥力严格控制距离,那么只要调整斥力的作用距离就可以设置各节点的分散程度,从而控制节点的覆盖率。如此,节点间斥力的大小可以表示为:
Fr=Kr/dij2
(3)
其中:Kr为斥力系数,dij为两节点si和sj间的距离。
3)对于节点间斥力作用范围的设置,在此方案的设计中决定了它们的重叠面积从而影响了整体覆盖率。通常认为的最佳的覆盖方式是无缝覆盖的同时重叠覆盖的面积尽可能小。那么根据几何学的有关知识,多个相同的圆实现无缝覆盖平面区域主要有如图2所示的几种设置方法。
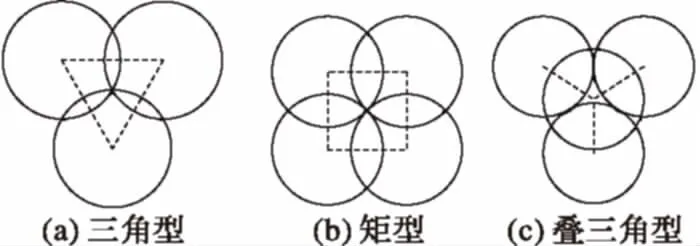
图2 无缝覆盖的三种方案
由图2可见,在无缝覆盖的几种方式中图2(a)所示的是最佳的方案,这种设置方法在实现无缝覆盖的同时,重叠的面积最小,也就是说其覆盖的范围最大,故以此方案为参考设置基站间产生斥力的距离。
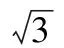
综上所述,节点间的斥力可以表示为:
X方向:
Frx=Kr×Δxr/dij2
(4)
Y方向:
Fry=Kr×Δyr/dij2
(5)
其产生作用的距离为:
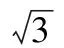
(6)
其中,Kr为斥力系数,Δxr和Δyr分别为节点sj指向si单位距离矢量的X方向分量和Y方向分量,dij为其距离标量,R为节点覆盖半径。
2.1.3 引力线
上述虚拟力的设置只能实现目标的按需覆盖,为了将各目标间的传感器节点通信连接起来,引入引力线的方法。
将某两个目标所确定的直线或线段称为引力线,引力线实际上并不存在,只是用来指导节点的运动。一定范围内的节点会受到垂直指向引力线的虚拟引力作用而靠近引力线。当节点运动到引力线附近时,可能出现节点在引力线附近振荡的情况,所以在引力线上设置较窄宽度的“真空带”,当节点运动到“真空带”内则不受引力线的虚拟力。需要注意的是,当目标数增多时,引力线也会随之增加,可能导致局部受力情况过于复杂。为了避免这一现象出现,每个节点可以在初始状态时先判断距离自己最近的引力线,在之后的调整中则只受到该引力线的作用,这样可以简化节点的受力情况,但同时并不影响部署效果。引力线产生的引力的大小与目标引力的设置相同,与节点到引力线的距离的平方成反比,如下:
X方向:
Flx=Kl×Δxl/dl2
(7)
Y方向:
Fly=Kl×Δyl/dl2
(8)
其中:Kl为引力线引力系数,dl为节点到引力线的距离,Δxl和Δyl分别表示由节点垂直指向引力线的单位方向矢量的X和Y方向的分量。
如图3所示,c1、c2为两个目标,L为过两目标的引力线,节点s1受到其引力Fl的作用垂直向引力线运动,当节点运动到“真空带”,即外侧的两条虚线之间的时候,则不再受到引力线的引力,可能受到其他节点的斥力而沿着引力线运动,使得各节点沿引力线排列开来,从而连接两个目标之间的其他节点。
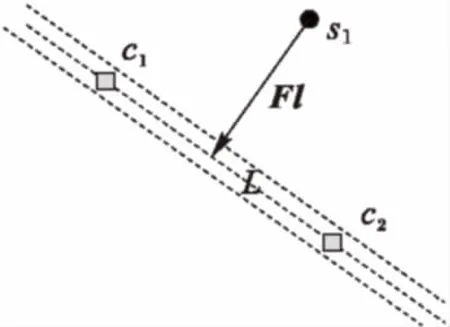
图3 引力线示意图
2.2 算法步骤
初始情况是,在某一L×W的平面监测区域内,分布着若干或集中或分散的节点,以及待覆盖的若干目标。这时所有节点在当前所处的情况计算一次在监测区域内受到的虚拟力的合作用力,根据所受的合力进行一定量的移动,然后节点再根据新的位置进行同样的计算,如此重复迭代计算直到部署完成。
上文介绍了整个监测区域中虚拟力场主要由目标产生的引力、引力线的引力和节点间的相互斥力构成,那么节点所受的合力就是它们的矢量和,具体对于某节点si,其所受的合力可以表示为:
X方向:
(9)
Y方向:
(10)
其中:第一项表示节点i受到来自目标ck的引力的分量之和,第二项表示节点i受到来自邻居节点j的斥力的分量之和,第三项表示节点受到引力线的引力。
由于上述合力是矢量和,所以通过计算合力可以得到节点需要移动的方向和距离,但是由于节点间斥力较大,节点所受的合力的值可能较大,故其所受合力的标量不能直接作为其移动的距离值,还需要对其移动距离和合力的关系进行合理的设置,控制其上限。考虑到反正切函数存在上界的情况,此处将节点所受合力的标量值作为反正切函数的自变量进行处理,即如下所示:
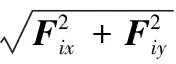
(11)
其中:li为节点si单次移动的距离[15],Fix和Fiy分别为节点si所受的合力的X方向和Y方向分量,b为节点移动步进。上式可以将节点的移动距离上界限制在b。
此外,由于节点分布的随机性,在部署接近完成时,可能出现节点位置振荡而难以趋于稳定的情况。针对这一情况,可以采用节点移动步进b来控制算法的收敛,实际应用时应根据具体环境设置b的值,例如随迭代次数增加而衰减或与实际节点移动的速度有关。此外还应设置节点移动停止门限δ,当节点计算得到移动的距离小于δ时认为达到稳定状态,节点停止移动[16],这也可以较好地避免节点振荡的情况。
节点移动的方向即其所受合力的方向,那么根据计算的节点移动距离和方向在节点原坐标的基础上进行更新即可得到移动后的新的位置坐标。
算法的步骤如下:
1)
初始化设置:监测区域范围L×W,目标位置C,区域内节点集S,节点初始位置,节点覆盖半径R,初始迭代次数n=0,最大迭代次数nmax,节点移动步进b,移动停止门限δ。
2)
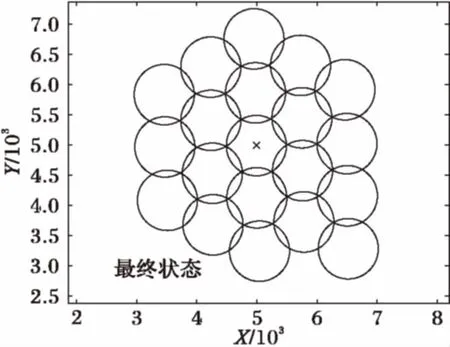
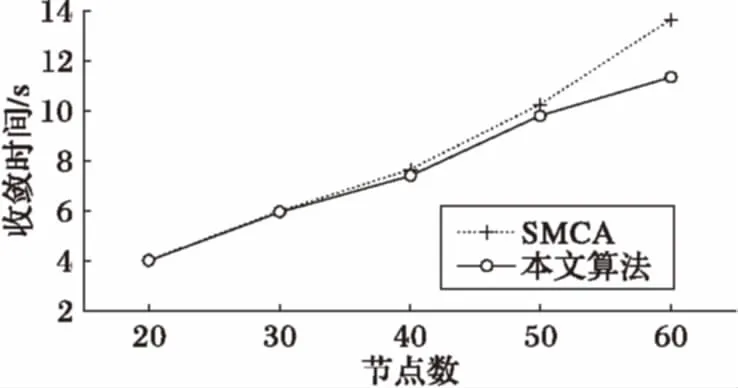
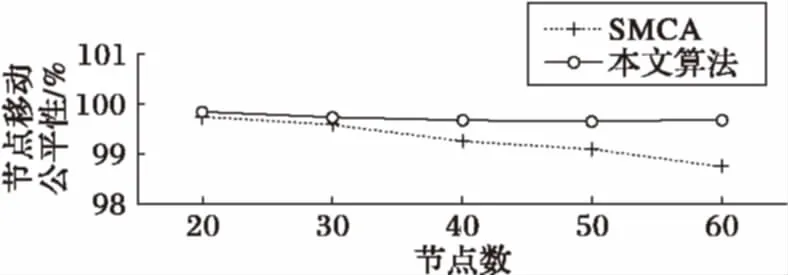
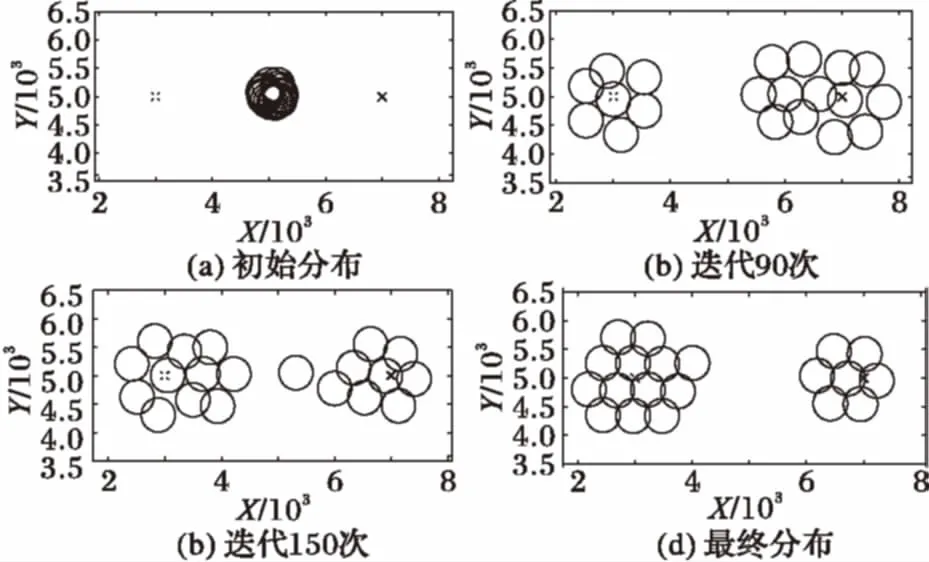
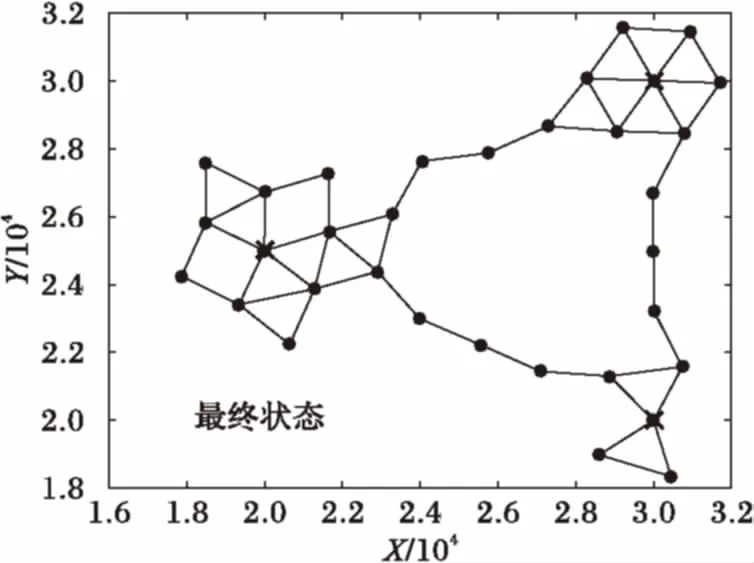
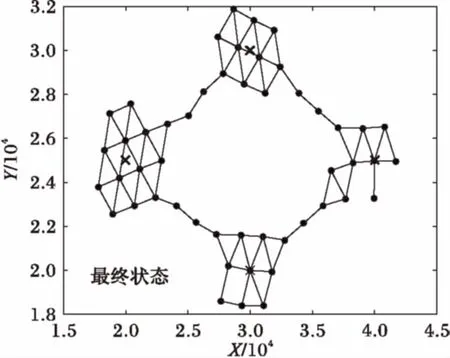
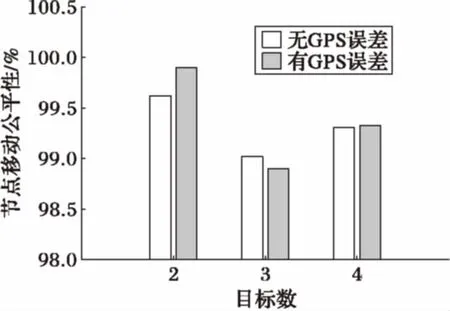
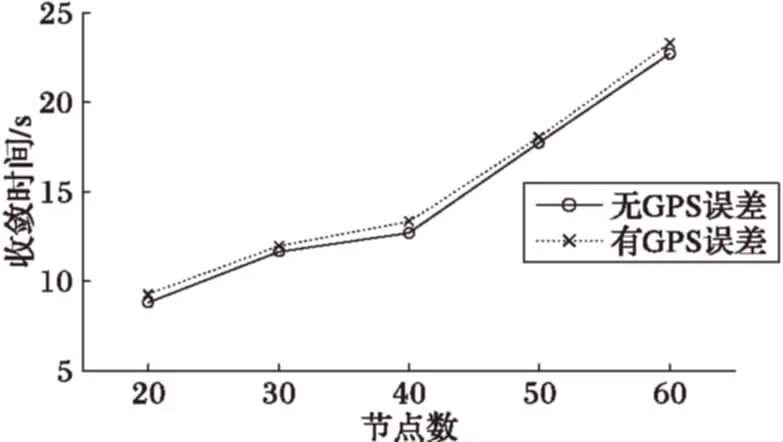
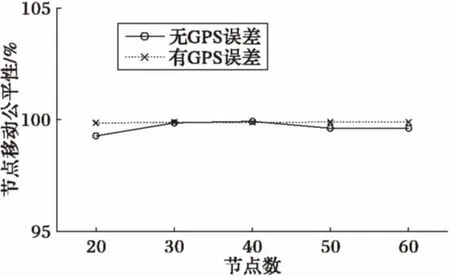
Whilen 3) Forn 4) Forsi∈S 5) 计算节点距离最近的引力线 6) 计算节点受到引力线的引力 7) Forck∈C 8) 分别计算ck对节点的X方向和Y方向引力 9) End for 10) Forsj∈S≠si 11) 12) 节点间斥力Fr=0 13) Else 14) 分别计算节点sj对si的斥力的X方向分量和Y方向分量 15) End if 16) End for 17) 计算节点si所受的合力的X和Y方向分量 18) 计算节点si的移动距离和方向 19) 移动并更新节点si的位置 20) End for 21) End for 22) End while 2.3 收敛性分析 节点在初始分布时,受到较大的斥力(密集初始条件)或引力(稀疏初始条件),对应的每次移动的距离也较大。之后所受合力可能逐渐减小,当趋于稳定时,节点所受的合力趋于零,移动的距离也趋于零。对于这种情况,由于节点单次移动的距离是反正切函数,故当合力趋于零时,节点的移动距离也随之趋于零,则必然∃δ0>l,此时可认为算法收敛。对于另外一种情况,若节点所受合力不趋于零,而是出现振荡(这主要是由于节点所受斥力较大,计算得到的移动距离较大,但移动后又脱离了斥力的范围而受到引力吸引,从而使得节点在最佳距离附近振荡),则由步进值b可以控制减小其移动距离,当节点与其所接近的目标距离小于一定的值时,利用步进值b减小其移动的距离,可以使节点稳定于最佳位置附近。综上两种情况,算法最终可以收敛,使得节点部署趋于稳定。 首先对本文仿真实验所设置的参数进行说明,需要注意的是,本文所研究的应用背景具有较强的特异性,不同的环境应用时差异较大,将会导致参数设置上的差别,实际中应根据当时的应用环境相应地调试有关参数,以达到理想的效果。此外,文中各量均作无量纲处理,重点关注它们之间的比例关系和便于理解。 引力和斥力系数的设定与区域大小和节点覆盖半径有关,本文参考文献[13]将引力系数设置为与区域边长同量级,斥力系数为引力系数10倍。力的系数太小或太大均会影响部署效果和收敛时间。 对于最大迭代次数nmax,本文设置了一个较大的值500来限制程序运行可能出现的假死或无限循环的异常情况,通常程序运行达不到这一上限即可收敛。 对于移动停止门限δ,是用来判断算法是否收敛的条件,本文算法中,节点所受合力应逐渐减小至0,但是实际中合力可能无法完美达到零,或是会经过极多甚至无穷次迭代,所以引入节点移动停止门限是十分必要的。通常节点的移动距离维持在一个较小的值时可以认为其已经在最佳位置附近小幅振荡,设置一个停止门限可以避免节点无止境的振荡。考虑到节点感知半径为500,停止门限应远小于这一值,例如相差一个量级以上,故本文结合仿真实验经验将其设置为20。 3.1 单目标覆盖 图4中叉号代表目标位置,圆圈表示节点的覆盖范围,节点位置位于圆心(坐标轴刻度为对平面区域如第1节所述建立坐标系时的位置刻度,图4中坐标轴X、Y方向无量纲,单位为1,下同)。由图可见节点围绕目标部署,且目标周围的节点之间实现无缝覆盖。 图4 单中心覆盖结果示意图 将本文算法应用于单目标时的性能与文献[13]中的SMCA(Simple Movement Control Algorithm)进行比较,主要考察了算法的收敛时间和节点移动的公平性。其中:收敛时间指从初始位置开始到完成部署所用的时间;节点移动公平性采用了Jain氏公平性指数: (12) 在本文中,n即节点数,xi即节点i移动的总距离,计算结果f(x)即为公平性指数。该数值无量纲且处在0~1,越接近1说明越公平,反之说明公平性差。为便于阅读,本文将该数值表示为百分数形式。 图5可见本文算法的收敛时间较SMCA方法稍短,尤其在节点数相对多时,且考虑到实际应用中算法分别由各节点分布式计算,执行效率应更高。 图5 两种算法收敛时间比较 图6显示了本文算法的节点移动公平性明显好于SMCA算法,且本文的该项指标较稳定,基本不随节点数而变化。 图6 两种算法节点移动公平性比较 3.2 两目标动态按需覆盖 此处在不引入引力线的情况下演示两个目标的动态按需覆盖过程,其中当迭代次数达到100后将调整目标的引力系数以模拟覆盖需求变化的情况。 由图7可见(图中坐标轴X、Y方向无量纲,单位为1,叉号代表目标位置,圆圈表示节点的覆盖范围,节点位置位于圆心),在迭代100次之前节点按照左侧目标覆盖需求小而右侧大的设定进行部署,当迭代100次后目标需求发生了变化,原来需求小的左侧目标需求变大,节点也根据新的需求调整部署,一部分节点从右侧移动到了左侧,说明本文算法可以适应目标需求的变化。 图7 两目标动态按需覆盖过程 3.3 多目标连通按需覆盖 图8、9中叉号处为各目标位置,圆点为节点位置,圆点之间的连线表示节点之间处于可以通信的范围(图中坐标轴X、Y方向无量纲,单位为1)。显然,图中各目标周围根据不同的需求情况覆盖了一定的节点,同时各目标之间还有若干节点将节点集群连接起来,保证了所有节点间的通信连接,达到了本算法的设计目的。 图8 三目标连通按需覆盖部署示意 图9 四目标连通按需覆盖部署示意 在性能分析中考察了在目标数为2个,节点数分别为20、30、40、50、60时的收敛时间和节点移动公平性;以及在节点数为50个,目标数分别为2、3、4时的相应性能。考虑到实际应用中通常采用GPS进行定位,其精度直接影响了结果,故同时考察了GPS误差[17]对性能的影响。GPS误差的引入方法为:在计算出节点下一次将要移动的位置后,在该坐标的基础上加上一个随机方向的GPS定位误差值,以模拟定位与实际位置产生一定偏差时的情况。 图10对目标数分别为2、3、4,节点数为50时的收敛时间进行了考察。当目标数增加时收敛时间相应增加,符合实际情况。在引入GPS误差后,收敛时间相应增加,这是因为此时节点移动的位置并不是预期的精确计算结果,那么经过多次迭代积累下来可能导致较大偏差使得收敛时间大幅增加。但本文算法中收敛时间增加并不明显,大约在1%左右,最大也不超过5%,在通常的工程应用中处在可以接受的范围,说明本文算法对GPS误差容忍性较好,也就是说即使存在GPS误差,本算法也可以实现预期的部署效果。 图11对节点数为50,目标数分别为2、3、4时的节点移动公平性进行了分析。该指标都在99%左右,已达到很高水平,但在引入GPS误差前后不同目标的该项指标无明显规律,这主要是由于该项指标与目标数目和它们之间的相对位置有较大关系,由具体环境决定。部分节点在没有误差时可能率先到达停止条件,而引入GPS误差后这些节点相比没有误差时增加了移动量,与其他节点的移动总量差缩小,从而整体节点移动公平性更优。但是GPS误差的影响已经小于0.3%,可以忽略,认为没有影响。 图10 不同目标数收敛时间及GPS误差分析(50节点) 图11 不同目标数节点移动公平性及GPS误差分析(50节点) 图12是在2目标情况下分析不同节点数的收敛时间,当节点增加时,收敛时间增加,符合一般常识。GPS误差对此影响较小,这是因为每个节点都存在随机GPS误差,从整个系统来看,各节点之间的误差影响相互抵消了相当一部分,这也可以理解为整个系统分布式并行计算结构的鲁棒性。从量级上看,GPS误差引入前后收敛时间的变化不大于5%,在实际应用中可以接受。 图12 不同节点数收敛时间及GPS误差分析(2目标) 图13反映了2目标不同节点数的节点移动公平性,可见本文算法节点移动公平性十分接近1,效果好。引入GPS误差后性能相近或略好主要是因为潜在提高了节点间的交互性,和对图11分析相同,增加了移动量较少节点的总移动量,减小了各节点移动量分布的方差。实际上由于GPS误差对该指标影响小于1%,故可认为在一般系统误差范围内无影响。 图13 不同节点数节点移动公平性及GPS误差分析(2目标) 本文提出了一种基于虚拟力的移动传感器网络节点连通按需覆盖的部署方法。该方法针对传感器监测区域中存在覆盖需求不同的目标的情况,通过设置目标产生引力吸引节点向目标区域移动,节点之间产生斥力使之避免重叠,引入引力线使得各目标之间节点相互连通,通过节点分布式逐轮计算后移动,从而实现了对监测区域中需求高的目标部署较多节点,对需求低的区域部署较少节点,各目标之间节点保持通信连接,目标周围节点之间实现无缝覆盖的按需覆盖。该算法部署效果佳,收敛时间短,节点移动公平性高,GPS误差并未明显降低本算法性能,实际应用的价值高。后续的工作可以考虑优化节点的移动效率,以及改进算法用于更广泛的异构网络中。 References) [1] LEE H J, KIM Y H, HAN Y H, et al. Centroid-based movement assisted sensor deployment schemes in wireless sensor networks [C]// Proceedings of the 2009 IEEE 70th Vehicular Technology Conference Fall. Piscataway, NJ: IEEE, 2009: 1-5. [2] CORTÉS J, BULLO F. Coordination and geometric optimization via distributed dynamical systems [J]. SIAM Journal on Control and Optimization, 2005, 44(5): 1543-1574. [3] BARTOLINI N, BONGIOVANNI G, PORTA T L, et al. Voronoi-based deployment of mobile sensors in the face of adversaries [C]// Proceedings of the 2014 IEEE International Conference on Communications. Piscataway, NJ: IEEE, 2014: 532-537. [4] MAHBOUBI H, AGHDAM A G. Distributed deployment strategies to increase coverage in a network of wireless mobile sensors [C]// Proceedings of the 2013 American Control Conference. Piscataway, NJ: IEEE, 2013: 5887-5892. [5] 黄帅,程良伦.一种基于虚拟力的有向传感器网络低冗余覆盖增强算法[J].传感技术学报,2011,24(3):418-422.(HUANG S, CHENG L L. A low redundancy coverage-enhancing algorithm for directional sensor network based on fictitious force[J]. Chinese Journal of Sensors and Actuators, 2011, 24(3): 418-422.) [6] 秦宁宁,余颖华,吴德恩.移动混合传感网中节点自主部署算法[J].电子与信息学报,2016,38(7):1838-1842.(QIN N N, YU Y H, WU D E. Autonomous deployment algorithm in mobile heterogeneous networks [J]. Journal of Electronics and Information Technology, 2016, 38(7): 1838-1842.) [7] IMAI H, IRI M, MUROTA K. Voronoi diagram in the Laguerre geometry and its applications [J]. SIAM Journal on Computing, 1985, 14(1): 93-105. [8] HOWARD A, MATARIC M J, SUKHATME G S. Mobile sensor network deployment using potential fields: a distributed, scalable solution to the area coverage problem [C]// Proceedings of International Symposium on Distributed Autonomous Robotic Systems 5. Berlin: Springer, 2002: 299-308. [9] 田一鸣,陆阳,魏臻,等.无线传感器网络虚拟力覆盖控制及节能优化研究[J].电子测量与仪器学报,2009,23(11):65-71.(TIAN Y M, LU Y, WEI Z, et al. Research on energy-efficient optimization for coverage control in wireless sensor networks [J]. Journal of Electronic Measurement and Instrument, 2009, 23(11): 65-71.) [10] 陶丹,马华东,刘亮.基于虚拟势场的有向传感器网络覆盖增强算法[J].软件学报,2007,18(5):1152-1163.(TAO D, MA H D, LIU L. A virtual potential field based coverage-enhancing algorithm for directional sensor networks [J]. Journal of Software, 2007, 18(5): 1152-1163.) [11] ZOU Y. Coverage-driven sensor deployment and energy-efficient information processing in wireless sensor networks [D]. Durham, North Carolina: Duke University, 2004. [12] GAGE D W. Command control for many—robot systems [EB/OL]. [2016- 12- 12]. https://www.researchgate.net/publication/243636092_Command_control_for_many-robot_systems. [13] LIU H, CHU X, LEUNG Y W, et al. Simple movement control algorithm for bi-connectivity in robotic sensor networks [J]. IEEE Journal on Selected Areas in Communications, 2010, 28(7): 994-1005. [14] SEMNANI S H, BASIR O A. Semi-flocking algorithm for motion control of mobile sensors in large-scale surveillance systems [J]. IEEE Transactions on Cybernetics, 2015, 45(1): 129-137. [15] LI S, XU C, PAN W, et al. Sensor deployment optimization for detecting maneuvering targets [C]// Proceedings of the 2005 8th International Conference on Information Fusion. Piscataway, NJ: IEEE, 2005,2: 1629-1635. [16] 周浦城,崔逊学,王书敏,等.基于虚拟力的无线传感器网络覆盖增强算法[J].系统仿真学报,2009,21(5):1416-1419.(ZHOU P C, CUI X X, WANG S M, et al. Virtual force-based wireless sensor network coverage-enhancing algorithm [J]. Journal of System Simulation, 2009, 21(5): 1416-1419.) [17] National Coordination Office for Space-based Positioning, Navigation, and Timing. GPS accuracy [EB/OL]. [2017- 03- 20]. http://www.gps.gov/systems/gps/performance/accuracy/. Distributeddeploymentalgorithmforconnectedon-demandcoverageinmobilesensornetwork MAO Lingchu*, ZHAO Haitao (CollegeofElectronicScienceandEngineering,NationalUniversityofDefenseTechnology,ChangshaHunan410073,China) Aiming at the problem that the number of sensors needed in the monitoring area of the mobile sensor network is different and no path is formed between the targets, a method of on-demand coverage for different targets was proposed by virtual force method. The attractive force between targets and sensor nodes based on the gravitational attraction, the repulsive force based on the Coulomb force between nodes and the gravitational lines between targets were set according to the coverage requirements of different targets. The nodes covered the targets or formed the paths under the guidance of its resultant force. The simulation results show that the proposed method has a shorter convergence time compared with the existing representative algorithm, and the moving fairness index is as high as 99%, and the influence of GPS error can be controlled below 1%, which can be distributed under sparse or dense initial conditions. mobile sensor network; on-demand coverage; virtual force; gravitational line 2017- 03- 27; 2017- 05- 05。 国家自然科学基金资助项目(61471376)。 毛凌楚(1993—),男,湖南长沙人,硕士研究生,主要研究方向:无线传感器网络、多智能体网络; 赵海涛(1981—),男,山东昌乐人,副教授,博士,主要研究方向:认知无线网络、智能组网、交叉层协议设计与优化。 1001- 9081(2017)09- 2463- 07 10.11772/j.issn.1001- 9081.2017.09.2463 TP393.02 A This work is partially supported by the National Natural Science Foundation of China (61471376). MAOLingchu, born in 1993, M. S. candidate. His research interests include wireless sensor network and multi-agent network. ZHAOHaitao, born in 1981, Ph. D., associate professor. His research interests include wireless cognitive network, intelligent networking, network protocol design and optimization.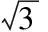
3 仿真实验
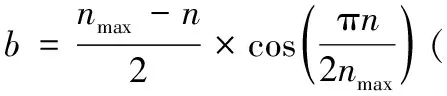
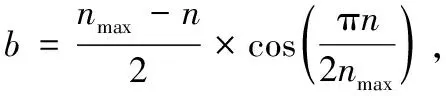
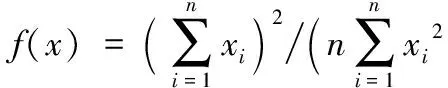
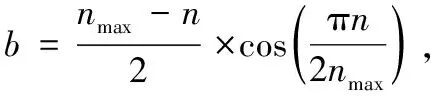
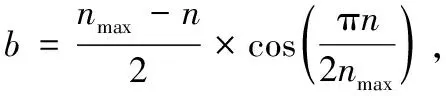

4 结语
